一种主从MEC服务器协作卸载与资源分配方案*
2022-04-26鲜永菊宋青芸郭陈榕
鲜永菊,宋青芸,郭陈榕,刘 闯
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
移动设备受限于小巧的体积,在计算能力与能耗方面有较大的局限。移动边缘计算(Mobile Edge Computing,MEC)通过将云计算能力下沉至移动终端侧,可以近距离为移动用户提供计算服务,有助于用户高效地执行任务,减少能耗,提高执行任务能力[1]。
尽管MEC具有许多优势,但MEC服务器自身有限的计算能力仍会带来许多挑战,主要体现在计算资源供需不平衡,特别是部署在热点小区(商圈、密集住宅区)中的MEC服务器,将面临大量任务卸载请求,若无法及时处理众多请求,会导致用户体验降低[2]。针对此类问题,文献[3-6]通过拒绝、推迟或任务排队的方式来缓解MEC服务器过多的工作量,虽然改善了资源有限的问题,但可利用的资源没有得到扩展。因此,越来越多的学者将目光投向宏观场景下的多MEC服务器协作。
协作通信被广泛应用在移动通信网络中。多MEC服务器协作需要对MEC服务器的实时信息进行控制,当前主流的方案主要是软件定义网络(Software Defined Network,SDN)集中控制与分布式控制[7-9],现有的研究通常忽略两种方案由于信息交互带来的能耗与时延,而专注于制定卸载策略。
关于MEC服务器协作卸载的研究,文献[10]针对协作小区之间的组合问题,提出了一种基于博弈论的任务分组方案,将多个热点小区与非热点小区生成多个协作集,但未具体研究协作集内的卸载与资源分配;文献[11]研究了两个边缘节点之间的协作,以最大化降低时延,该问题通过遗传粒子群算法求解,但文献中涉及到的MEC服务器数量较少,并且无法保证启发式算法解的稳定性;文献[12]在能耗约束下提出了最小化时延的优化问题,并设计算法将多个任务协作到多个MEC服务器组成的集群中,但未优先将任务卸载至本小区的MEC服务器上,这可能会影响其他小区执行自身的任务;文献[13]通过一种迭代更新方法将主MEC服务器过量的任务卸载至其他MEC服务器,但未对计算资源进行分配;文献[14]提出了一种MC-GBA算法,可以依据代价将主MEC服务器中过量的任务卸载至从MEC服务器,实现计算资源的扩充;文献[15-17]通过远端云中心与本地MEC实现多级卸载,并分别通过任务属性、任务需求以及资源剩余划分出不同的卸载用户。
基于以上研究,本文采用主从MEC服务器协作卸载的方式,以改善热点小区内计算资源有限的问题。在主从MEC系统中,通过SDN的集中控制,主MEC服务器将自身无法完成的任务二次卸载至附近仍有可利用计算资源的从MEC服务器进行计算,实现了计算资源的拓展。为了最小化热点小区内请求用户执行任务的总代价,本文提出一种基于主从MEC系统的任务联合卸载方案,依次分析了不同属性任务以及从MEC服务器数量对方案的影响,并与其他卸载方案对比验证了所提方案的有效性。
1 系统模型
1.1 网络场景
在一个多小区计算场景,每个小区内有一个MEC服务器部署在基站侧,负责处理本小区内产生的计算任务,多小区之间通过SDN控制器集中控制,结构如图1所示。MEC服务器和用户均可通过基站与SDN控制器进行信令传递,SDN控制器收集各个服务器可提供的计算资源并对资源池进行更新,这样,SDN可以集中控制多个小区内的计算任务卸载以及资源分配。
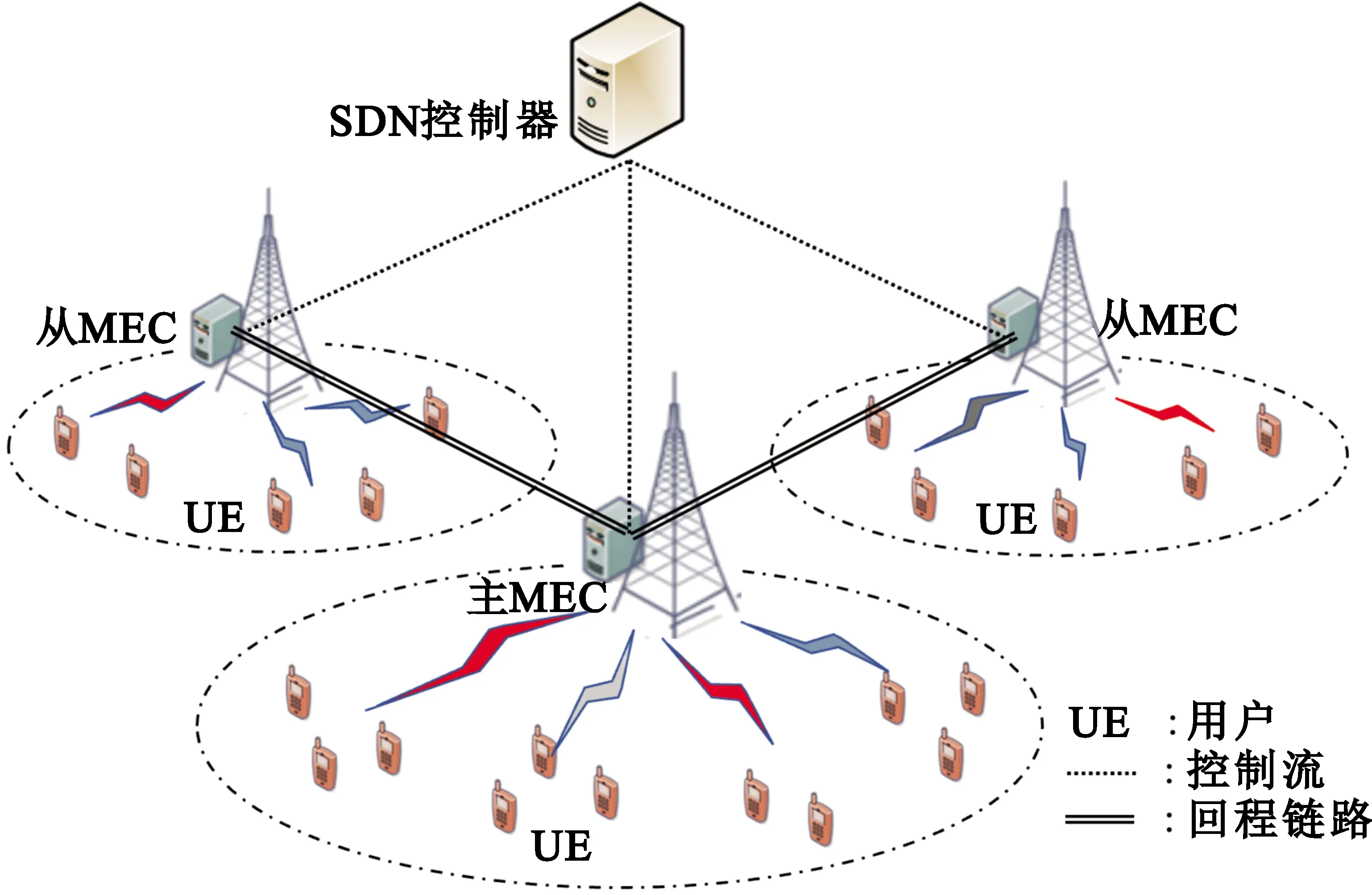
图1 基于SDN集中控制的主从MEC系统结构
本文研究热点小区(主小区)内的高负载任务卸载优化,将热点小区MEC服务器无法完成的计算任务二次卸载到周围尚有计算资源的小区(从小区)进行计算。这个过程中,暂不考虑从小区内的任务,只让从小区充当辅助计算节点,同时忽略集中控制信令传递所需的时延与能耗。此外,主小区内任务不可拆分,即任务执行只有本地执行、主MEC服务器执行以及从MEC服务器执行三种状态,同时假设每个用户携带一个计算任务。

1.2 通信模型
用户通过无线网络与MEC服务器进行交互。为了简化问题,假设在同一小区内多用户占用相等且不相交频谱资源,并且不考虑小区内部通信干扰。任务上行速率为
(1)
式中:Ptra,i表示用户i的发送功率,gi表示用户i与MEC服务器之间的信道增益,N0表示信道单位噪声与干扰的功率谱密度。用户通过无线信道上传任务花费时延与能耗分别为
(2)
(3)
由于MEC服务器返回任务结果数据量很小,任务结果传回用户的时延将忽略。
考虑MEC服务器间通信,主MEC服务器与从MEC服务器通过有线链路相连,主MEC服务器到从MEC服务器方向的传输速率为rM,此部分不涉及到用户能耗代价,MEC服务器之间任务传输的时延为
(4)
1.3 计算模型
1.3.1 本地计算
设用户终端的计算能力为floc,i,任务在终端本地执行的时延与能耗分别为
(5)
Ei,0=κibidi(floc,i)2。
(6)
式中:κi是与硬件架构相关的常数。记αi和βi为用户对于时延与能耗的权重系数,用户本地执行总代价为
Ui,0=αiTi,0+βiEi,0。
(7)
1.3.2 MEC服务器计算
任务如果卸载到MEC服务器执行,需要占用MEC服务器的计算资源。记Fj表示第j个MEC服务器可提供的总计算资源,Fi,j表示MEC服务器j为用户i分配的计算资源。
当任务在主MEC服务器执行,此时j=1,任务计算的时延与能耗可以分别表示为
(8)
(9)
这里用户产生的能耗为用户上传任务产生的能耗。那么,用户的总计算代价可表示为
Ui,1=αiTi,1+βiEi,1。
(10)
若任务在从MEC服务器执行,那么此时1 (11) 这里任务执行产生的能耗同样为用户卸载任务产生的能耗,表示为 (12) 用户的总计算代价为 Ui,j=αiTi,j+βiEi,j,1 (13) 综合考虑任务在MEC服务器端执行,可以将任务执行代价函数写为 (14) 记本地执行任务的决策向量集(卸载集)为A={a1,a2,…,an},其中ai∈{0,1},并且 (15) 卸载集A记录了每个任务是否卸载执行,其中卸载执行的任务还需选择目标MEC服务器。任务的多MEC服务器选择矩阵表示为 (16) 式中:bi,j∈{0,1},取值表示含义为 (17) A、B两个决策变量可以表示多任务卸载决策。对于计算资源分配,本文引入计算资源分配矩阵F,表示为 (18) 任务执行过程中,时延与能耗是用户感知明显的,也是任务在MEC服务器计算相对于本地计算最具有优势的性能指标。本文的优化目标是在主MEC服务器计算资源有限的情况下,最小化主小区内所有任务的执行代价之和。基于之前对系统模型的分析,优化问题P1可表示为 (19a) s.t.C1:ai∈{0,1} (19b) C2:bi,j∈{0,1} (19c) (19d) (19e) 对于优化问题P1,目标函数W中第一项表示本地执行的总代价,第二项表示所有卸载到MEC服务器中任务执行的总代价。约束条件C1、C2表示卸载决策变量ai与bi,j为0~1整数变量,约束条件C3保证任务只能在本地计算或在某一个MEC服务器上进行计算,约束条件C4保证在每个MEC服务器上计算资源在有限的范围内进行分配。 为最小化代价,需要得到优化变量A、B、F的最优解。但由于问题P1是一个混合整数非线性规划问题,并且优化函数中存在二元变量,导致该优化问题非凸,不能通过常规凸优化解法求解。 为求解优化问题,首先考虑原问题的三个优化变量。若已知需要卸载执行的任务(卸载集A的解),便可以通过一种方法得到MEC服务器选择矩阵B与计算资源分配矩阵F的解;同时,卸载集A的求解又受到矩阵B与矩阵F值的影响。综合以上分析,求解方案可设定初始卸载集A0,接着求得原问题松弛后的MEC服务器选择矩阵B与资源分配矩阵F,最后再对卸载集A进行优化。这样,可将原问题分解为部分任务卸载、多MEC服务器选择和计算资源分配三步求解。综上,基于主从MEC系统的联合卸载方案实现流程如图2所示。 图2 联合卸载方案流程图 当卸载集A与MEC选择向量集B确定之后,记本地执行的任务集合为N0,选择卸载到MEC服务器j执行的任务集合为Nj。此时,原问题P1可转化为 (20a) (20b) 由于不同MEC服务器的计算资源分配是相互独立的,所以不同MEC服务器的计算资源分配不相互干扰。为了使该问题更加清晰,进行未知变量替换。令ωi,1=1/Fi,1,ωi,j=1/Fi,j其中Fi,1≠0,Fi,j≠0,问题P2变为 (21a) (21b) 容易看出,优化问题P2′的优化目标函数以及约束条件均为凸函数,同时,ωi,j的可行域是连续的凸集,因此P2′是一个凸优化问题。通过构造拉格朗日函数并结合KKT(Karush-Kuhn-Tucker)条件,可得到优化问题P2′的最优解为 (22) 在主从MEC系统中,从MEC服务器负责执行主MEC服务器上过量的任务,因此,为了求解多MEC服务器选择,首先需确定可以在主MEC服务器上完成的任务集合N1,再将过量的任务分配给从MEC服务器。 规定所有可在主MEC服务器执行的任务需满足式(23)约束: Ui,1≤Ui,0,∀Ti∈N1, (23) 即对于集合N1中的所有任务,执行代价应小于本地执行代价。 为了在完成多MEC服务器选择的同时最小化任务执行代价,本文提出一种基于贪婪的多MEC选择算法(Greedy Based Multi-MEC Selection Algorithm,GBMS)。GBMS算法通过贪婪思想分阶段进行求解,对于多MEC服务器选择问题,该算法将较为容易地得到一个次最优解。 输入:多任务信息,主、从MEC服务器信息、集合Na。 for l=l+1; N1,l=N1,l-1∪{Tl}; else Nc,l=Nc,l-1∪{Tl}; N1,l=N1,l-1; end if end if if(l==L) break; end if end for 根据集合N1,l与集合Nc,l生成多MEC服务器选择矩阵B。 输出:最终代价U(N1,L)+U(Nc,L),多MEC服务器选择矩阵B。 算法保证了二次卸载的任务是主MEC服务器过量的任务。在算法中,主MEC服务器上任务代价U(N1,l)容易求解,但从MEC服务器上任务执行代价U(Nc,l)需要将过量任务匹配到M-1个从MEC服务器上后才可求解。 为了更清晰地表述集合Nc中最小化任务代价的问题,假设此时集合Nc中共有N′个任务。另外,在这个问题中只需要考虑M-1个从MEC服务器。因此,本文引入任务分配矩阵Z=(zi,j)N′×M-1,zi,j∈{0,1}表示要求解的矩阵。此时,最小化集合Nc中任务代价的问题为 (24a) s.t.C1:zi,j∈{0,1}, (24b) 问题P3中目标函数W′是原问题P1目标函数W去除已确定在主MEC服务器与本地执行的任务后的目标函数,约束条件保证每个任务都只能在一个从MEC服务器上执行。对于该问题,将会有2N′+1种选择,是NP-hard问题。 为有效解决这个问题,本文通过一种连续变量替换结合迭代近似的方法进行求解[18]。首先对原优化问题进行变量近似替换,引入连续变量vi,j。vi,j有以下性质: (25) 另外设定线性函数V(vi,j),其表达式为 (26) 式中:ε是一个小值,t是迭代次数。接着,用vi,k替换P3约束条件中的zi,j,用V(vi,j)替换P3表达式中的zi,j,替换变量后的问题是凸优化问题[18],容易求解。 (27) 输入:从MEC服务器执行任务集合Nc,从MEC服务器信息。 初始化:t=0; 对集合Nc中的计算任务: for t=t+1; 将式(22)代入问题P3,并替换变量; break; end if end for 输出:任务分配矩阵Z、二次卸载任务代价U(Nc)。 完成多MEC服务器选择以及计算资源分配之后,通过卸载集更新策略对上一次卸载集A进行更新。为减少不必要的卸载,制定卸载更新策略为 (28) 当本地执行代价不大于卸载执行代价时,用户不进行任务卸载,这样确保单个用户执行代价不会过大,同时也不占用MEC服务器的计算资源。另外,结合图2所示流程图与卸载更新策略,当联合方案没有产生最终决策时,将尝试卸载本地执行且执行代价最大的任务。这是由于该任务最可能通过卸载减少代价,若该任务卸载无法带来代价的减少,则可认为方案已经得到最优解。 假设联合卸载方案一共进行S次迭代,每次迭代中需要执行GBMS算法、计算资源分配以及卸载集更新。其中,计算资源分配只需相应的值计算;GBMS算法通过一轮迭代遍历Na中所有用户,迭代次数为L,在每次迭代中,U(N1)的求解可直接计算得到,U(Nc)的求解需要通过二次卸载算法求得,二次卸载算法也是一轮迭代,迭代次数为T,故GBMS算法的时间复杂度为O(LT);卸载集更新中寻找到本地执行且代价最大的用户的时间复杂度为常数复杂度O(N)。因此,本文联合卸载方案的时间复杂度为O(NS+LTS)。 本文仿真基于Matlab平台,仿真参数设置为[3,13]:网络总带宽B为5 MHz,信道噪声与干扰的功率谱密度为-174 dBm/Hz,信道增益在[-50,-30]内呈均匀分布,用户i本地的CPU频率floc,i在[0.5,1]GHz中随机分布,并且其任务的数据大小bi在[600,1 000]kB中随机分布,单位任务计算量di在[200,600]cycle/b中随机取值,用户i的发射功率P=0.1 W,系数κ=10-27,默认状态下有40个用户请求卸载。主MEC服务器提供的CPU频率F1=20 GHz,从MEC服务器提供的CPU频率在[2,8]GHz内随机分布,MEC服务器之间有线链路传输速率为20 MB/s,默认状态下有5个从MEC服务器参与辅助计算。 在任务总计算量不变的情况下,本文方案中任务数据量与代价的关系仿真结果如图3所示。可以看到,总代价随数据量增加而增加。当数据量较小时,由于传输带来的卸载代价较少,方案将大量任务卸载,因此本地代价较低。随着任务数据量的增加,传输带来的卸载代价增多,方案决策任务在本地执行,因此本地代价增加。 图3 数据量与代价关系图 图4是当任务数据量不变时,任务执行代价随单位计算量增加的变化情况。可以看到,随单位计算量增加,总的代价也随之增加,本地代价先增加后减少,先增加是因为计算量增加导致的代价增加;当本地代价超过卸载执行代价时,本文方案会将任务卸载执行,因此在图中本地代价曲线下降,并可预期本地代价将逐步减少为零。 图4 单位计算量与代价关系图 图5为本文方案中从MEC服务器数量与用户卸载数量的关系,可以看到,随着从MEC服务器数量的增加,卸载到主MEC服务器用户的数量大体相同,这是因为本文方案将任务优先卸载到主MEC服务器执行。在这个过程中,观察到从MEC服务器执行的任务数量并不是以线性增长的。这是因为当大量用户卸载时,卸载代价也随之增加,受卸载更新策略的影响,方案会使一些任务在本地执行。 图5 从MEC服务器数量与用户卸载数量关系 从图6中可以看出本文方案随着从MEC服务器数量增加,系统总代价将减少。并且,观察到当从MEC服务器足够多时,卸载代价与本地代价将趋于稳定。这是因为当从MEC服务器数量增多,可以使更多任务卸载执行,但这也增加了任务传输的代价。因此,卸载代价与本地代价将逐渐趋于稳定。 图6 从MEC服务器数量与代价关系 从图7中可以看出随着请求卸载任务数量的增加,本文方案优先将任务卸载到主MEC服务器执行。当主MEC服务器执行的任务增多时,由于受到式(23)的限制,部分任务被卸载到从MEC服务器执行。最终当主MEC服务器与从MEC服务器无法再降低任务执行代价时,过量的任务将在本地执行。 图7 请求任务个数与实际卸载任务关系 图8为用户数量与任务执行总代价的关系,可以看到当用户数量较少时随机方案的代价最少。这是因为随机方案将任务随机分配给不同的MEC服务器,可利用的资源更多,而本文方案与MC-GBA方案将任务优先卸载至主MEC服务器,并没有利用从MEC服务器的资源。随着用户数量增加,本文方案可以获得最少的代价,这是因为本文方案不断地将最有可能减少代价的任务卸载,直到没有代价的更新,因此代价低于其他方案。 图8 用户数量与总代价关系对比 图9为从MEC服务器数量对系统总代价的影响。如图所示,在没有从MEC服务器时,本文方案的代价大于统一方案的代价。这是由于本文方案基于贪婪策略为主MEC服务器分配任务,得到的不是全局最优解,但贪婪思想可以减少计算复杂度。随着从MEC服务器数量增多,除统一方案与本地执行方案,其他方案可利用的资源增加,代价进一步降低。本文方案相比于MC-GBA方案对多MEC服务器中的任务分配更加合理,同时每次更新尽可能减少代价,因此,本文方案有最低的总代价。 图9 从MEC服务器数量与总代价关系对比 本文研究了主从MEC服务器的协作卸载问题,提出了一种联合卸载方案。方案每次迭代,首先根据设计的GBMS算法完成多MEC服务器选择,接着求解凸优化问题得到计算资源分配,最后更新卸载集,尝试卸载本地执行且代价最大的任务。仿真结果表明,所提方案能够缓解热点小区MEC服务器计算资源有限的问题,并有效降低请求卸载用户的总代价。 未来的研究目标是整合热区分集技术与任务卸载技术,设计有效的任务卸载方案,在更广泛的实际场景中提高MEC服务的可靠性与有效性。1.4 卸载模型与资源分配模型

1.5 最小化代价优化问题
1.6 优化问题分析与方案制定

2 联合卸载方案
2.1 计算资源分配
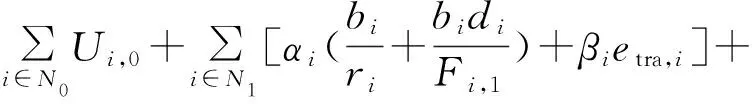

2.2 多MEC服务器选择
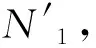
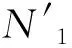
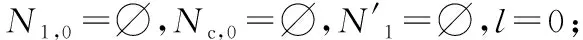
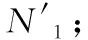
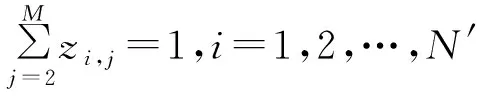

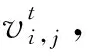

2.3 卸载集更新
2.4 联合卸载方案时间复杂度
3 仿真与分析
3.1 仿真参数设置
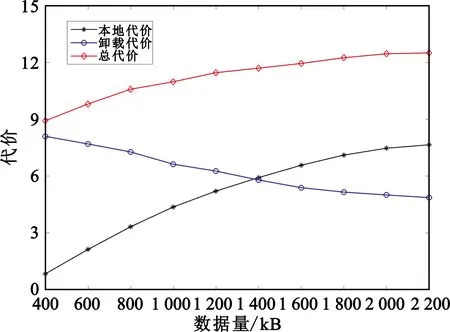
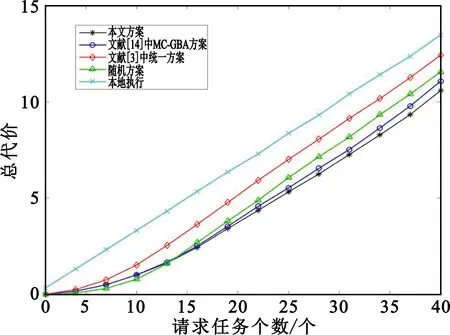
3.2 仿真结果分析





4 结束语
