电感耦合等离子体质谱法测定大气降水中钠的不确定度评定

崔胜红, 姚春强

不确定度是根据所用到的信息, 表征赋予被测量值分散性的非负参数。 测量不确定度表明了测量结果的质量, 在检测工作中具备测量不确定度的结果才更具备使用价值, 更能完整表达测量值。 是判定测量结果质量的依据[1-4]。 国标方法大气降水中的监测项目是用原子吸收分光光度法和离子色谱法分析,ICP-Ms 具有操作简便、 灵敏度高、 抗干扰能力强、 检测元素多、 线性范围广等优点, 因此本文以《测量不确定度评定与表示》(JJF 1059.1-2012)为依据, 用电感耦合等离子体质谱仪对降水中的Cu 进行测定, 对测定过程中标准溶液的配制, 校准曲线的拟合, 样品重复测定等方面引入的不确定进行评定, 并给出测量结果的合成扩展不确定度, 使测量结果更具使用价值和说服力。 降水样品的采集按照《酸沉降监测技术规范》(HJ/T 165-2004)[5]中的要求, 用降水自动采样器采集。

1 实验部分

1.1 实验原理

降水样品采集后, 用0.45 μm 的滤膜过滤, 待测, 并同时测定实验空白。

1.2 仪器与试剂

7700X 电感耦合等离子体质谱仪, 安捷伦有限公司;CPA120S Sartorius 电子天平, 德国; 0.45 μm 有机滤膜; 多元素混合标准溶液, 安捷伦。

1.3 仪器分析条件

仪器分析模式为He 模式, 射频功率1550 W, 射频1.00 V,采样深度8.0 mm, 矩管水平位置为0.3 mm, 垂直位置为-0.2 mm, 载气流量1.00 L/min, 辅助气0.90 L/min, 积分时间0.30 s, 重复次数3, 在线内标。

2 不确定度分析

2.1 数学模型

式中:ρ——降水样品中Na 的浓度, μg/L

A——待测元素的比率

a——校准曲线的截距

b——校准曲线的斜率

2.2 不确定度分量的评定

测量不确定度由若干分量组成, 本实验不确定度的来源主要由以下几个方面: (1)标准溶液的配制; (2)样品重复性测定; (3)校准曲线拟合; (4)仪器的波动。

2.2.1 不确定度的A 类评定

对降水样品中的Na 进行8 次连续测定, 测定结果见表1。对测定结果进行单侧检验, 取检出水平α 为5%。

表1 样品浓度测定结果Table 1 Sample concentration determination results

(1)对最大值进行检验:查表得临界值G1-α(n)=2.032。Gn＜G0.95(8), 所以最大值无异常。

(2)对最小值进行检验:得G0.95(8), 所以最小值也无异常。

(3)样品重复测定引入的不确定度按(JJF 1059.1-2012)计算, 测量数据呈正态分布, k 取测量平均值的标准不确定度以贝塞尔公式计算:

则测量平均值的标准不确定度为:

相对标准不确定度为:

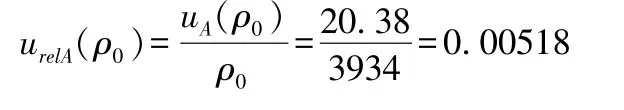
表2 样品不确定度A 类评定统计表Table 2 Sample uncertainty A evaluation statistical table

2.2.2 不确定度的B 类评定

2.2.2.1 校准曲线的配制引入的不确定度

(1)购买的安捷伦混合标准溶液, Na 的浓度为1000 mg/L,证书查得Ur=0.5%, k=2, 则由混合标准溶液引入的相对标准不确定度urel(cstock)=Ur/k=0.0025。

(2)用混合标准溶液配制标准中间液, 1%的硝酸介质, 采用重量法, 用万分之一的天平称量, 混合标准溶液的称量质量m0=6.3151 g, 中间液的最终质量m0终=61.0016 g, 标准中间液的配制引入的不确定度来源于天平的允差MPE, 由天平的检定证书查得0≤m≤5×104mg 时, MPE 为±0.4 mg; 5×104mg＜m≤2×105mg 时, MPE 为±0.5 mg, 按矩形分布考虑k 取3。则称量混合标准溶液引入的标准不确定度为0.231 mg, 则称量标准中间液的最终质量引入的标准不确定度为则urel(m0终)=

(3)由标准中间液配制标准曲线各点引入的不确定度, 按最高点计算。 曲线各点的称量质量见表3。

表3 标准曲线各点的称量质量Table 3 The weighing mass of each point of the standard curve

配制曲线最高点称量标准中间液引入的标准不确定度为

表4 配制标准曲线引入的不确定度B 类评定统计表Table 4 Type B evaluation statistics of uncertainty introduced by preparation of standard curve

将上述几个相对标准不确定度分量合成得由标准曲线配制引入的B 类不确定评定量值:

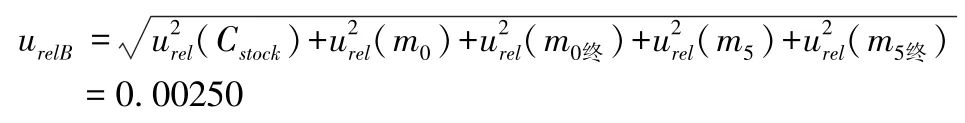
2.2.2.2 校准曲线拟合引入的不确定度

标准曲线的质量浓度分别为0.000、 59.824、 299.75、1031.6、 3061.4、 4024.3 μg/L, ICP-Ms 每个浓度点测定三次,用最小二乘法对测量数据进行线性回归, 结果见表5。

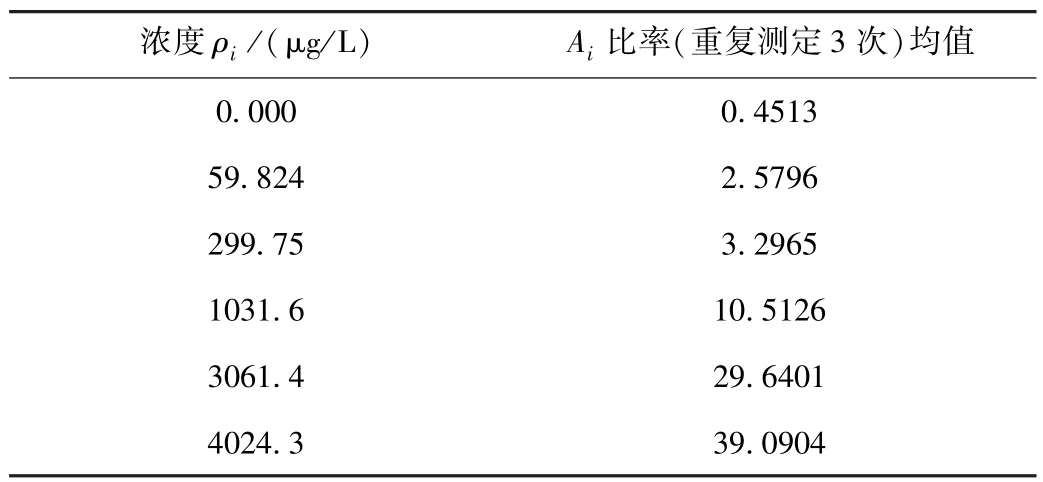
表5 校准曲线测定结果Table 5 Measurement results of calibration curve

由校准曲线拟合引入的标准不确定度按下式计算:

公中:S(A)为残差的标准偏差;b为校准曲线的斜率;p为样品的测定次数,p=8;n为标准溶液的测定次数,n=3;ρ0为降水样品中Na 测定浓度的平均值, μg/L;ρ

为不同校准溶液浓度的平均值;Sxx为校准曲线每一个点的浓度ρ与差的平方和, μg/L2。

Ai=0.481+0.00943ρi,r=0.9993

式(3)中残差的标准偏差计算如下:

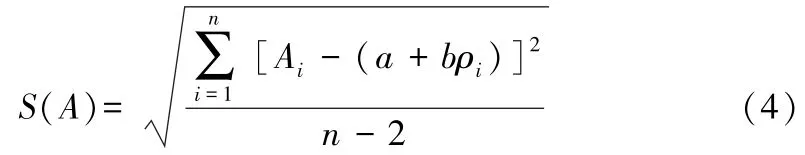
式中:Ai为校准曲线各点的响应值(比率),a + bρi根据校准曲线算出的各点的响应值(比率)。

由表5 数据经计算得S(A)=2.7476, 降水样品中Na 的平均浓度为ρ0=3934 μg/L,=1413 μg/L,Sxx=1.475×107(μg/L)2, 将算得的数据代入式(3)得:

则由校准曲线拟合引入的相对标准不确定度为:

2.2.2.3 仪器的波动

仪器的波动引入的不确定度已经在校准曲线拟合引入的不确定度评定中, 不再重复考虑。

3 不确定度的合成

各相对标准不确定度分量见表6。

表6 相对标准不确定度分量汇总Table 6 Summary of relative standard uncertainty components

根据不确定度的分量得到合成相对标准不确定度为:

合成标准不确定度为:

uc(Na)=ucrel(Na)×ρ0=275 μg/L

4 扩展不确定度

在95%的置信概率下,k =2, 扩展不确定度为:

U=k×uc(Na)=550 μg/L

该降水样品中钠的含量表示为(3.934±0.550)mg/L,k=2。

5 结 论

本文分析结果报告表明降水样品中钠的含量为(3.934±0.550)mg/L,k=2, 由上述不确定度分析过程可知影响ICPMs 测定降水中Na 的不确定度因素有: 标准溶液配制、 校准曲线拟合、 样品重复测定、 环境条件等, 其中主要影响因素是校准曲线的拟合。 所以在样品分析过程中, 注意调节实验室温湿度, 仪器预热足够时间, 仪器定期维护, 确保仪器处于最佳状态, 并注意标准溶液的配制不引入污染, 保证样品分析的每个环节, 使分析结果更加准确。