析结构 品解法 促深思——以一道自编题的解析为例

浙江省杭州市文海实验学校 吕德国 （邮编：310000）

数学是思维的体操，一个学生思维的广度，深度，灵活度往往决定了他在数学上的成就.那到底该如何锻炼学生思维呢？笔者认为，解一道好题是让思维提升的重要载体之一.解题教学是教学中一种常见的课型，教师析题品题的角度直接影响学生对问题思考的方向，教师对题目的研究能力更是直接影响到学生对问题理解的深度.如何让解题教学真实有效，以一道自编题为例，谈谈看法.

此题以圆为背景，先从几何位置关系出发，探求角的数量关系；再从角的数量关系出发刻画特殊的位置关系，牢牢抓住了圆中位置要素和特殊条件要素，体现了数形结合的思想，通过对题目条件的分析，阐释每种做法的由来，培养学生数学思维，提高几何问题的解决能力.

1 原题呈现

如图1，已知△ABC内接于⊙O（∠ACB＞90°），连接OA、OC.记∠BAC=α，∠BCO=β，∠BAO=γ.

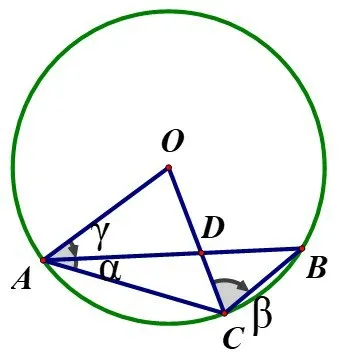
图1

（1）探求α与β之间的数量关系；

（2）设OC与AB交于点D，⊙O半径为1：

①若β=γ+45°，AD=2BD，求由线段BD、CD，弧BC围成的图形面积S；

②若α＋2γ=90°，设sinα=k，用含k的代数式表示线段AD的长.

2 思路分析

第（1）问中，求圆中两个角的数量关系，观察α和β的位置发现它们没有直接联系，但在圆中，可以利用圆心角定理，圆周角定理或者弧的关系，将角度转化到同一个三角形中，从而找到数量关系.

第（2）问①中，由前面可知∠α+∠β=90°，这个数量关系在∠ACB＞90°时恒成立.此时又给出β=γ+45°，联立，即可得α+γ=45°，从而发现一个非常特殊的角，即∠AOC=90°.此时A、O、C三点的位置是确定的.又AD=2BD，则A、D、B三点的位置也随之确定.图形确定的，那面积一定是可求的，

第（2）问②中，给出了α+2γ=90°这个数量关系，同样联立，会发现∠ABC=γ=∠OAD.也就是说在这种数量关系下，存在着特殊的位置关系，即AO∥BC，发现一组明显的八字形相似.题干中又给出sinα=k，可以得到BC=2k，利用刚才的八字形相似，得到AD=BD.发现这和①中所给的条件惊人相似.因为篇幅关系，这里只研究（2）中①的做法.

3 解法赏析

视角1特殊比例找相似

解法1题目中有1∶2 这个特殊比例，学生第一想法是相似，那题目中是否存在相似三角形呢？如图2，连接OB.

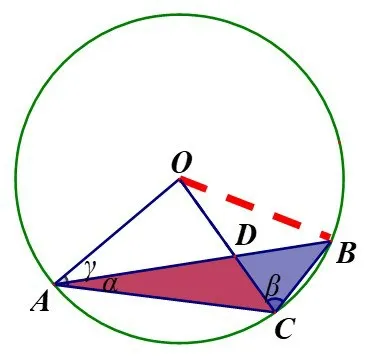
图2

由前面分析得到，∠DCA=∠CBA=45°，∠DAC=∠CAB，可以得到一组相似，即△ADC∽△ACB，所以，设DB=x，AD=2x，求得AD=，在Rt△AOD中，发现OD∶OA∶AD=1∶，所以γ=30°，所要求的面积S=S扇形OCB-S△ODB=

解法2除了解法1 中的三角形外，没有现成的三角形是相似的，那是否可以利用比例关系构造相似呢？学生最熟悉的是作平行线，如图3，构造相似，过B作BH∥OA.得到△ADO∽△BDH，所以，得到BH=，在Rt△OBH中，发现HB:OB=1:2，所以∠HOB=30°，那么面积S也就可以求得了.

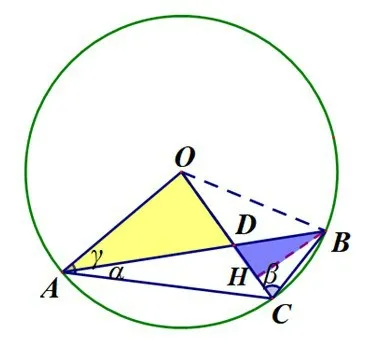
图3

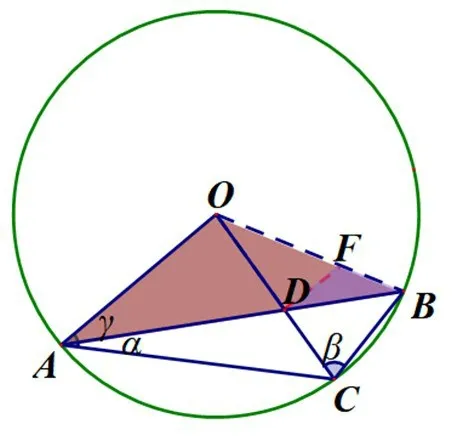
图4

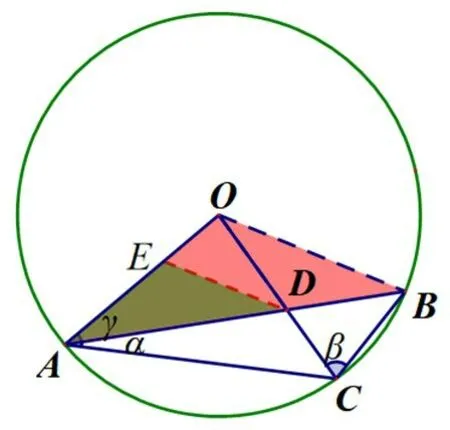
图5

解法5如图6，除了添平行线构造相似，还以作垂直构造相似，过点D作DF⊥OB.得到△BDF∽△ADO，所以=得到BF=那么OF发 现△ODB和△AOB均为等腰三角形，可以得到∠COB=30°，从而解决问题.

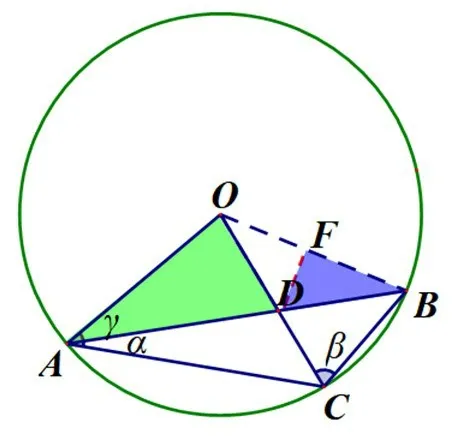
图6

视角2特殊直角做文章

解法6如图7，AB为圆中的弦，且∠AOD=90°，过O作AB的垂线交AB于点H，可以应用垂径定理，还有熟悉的“三垂直”图形.

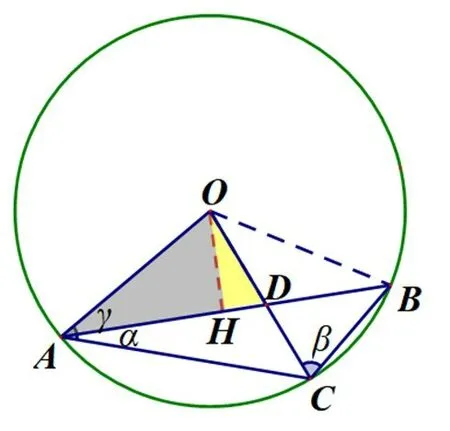
图7

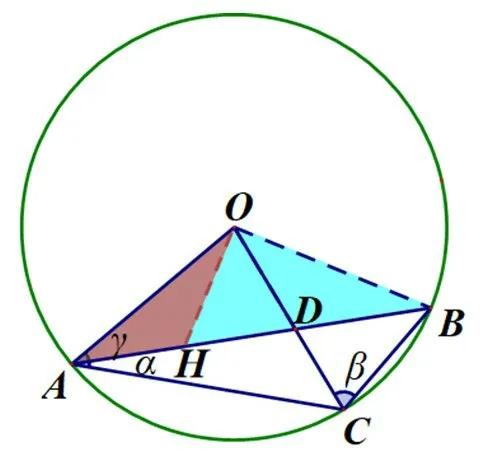
图8

视角3共性比例求面积

解法8条件AD=2BD，本质上是共线线段的比例问题，对于一维的线段问题，能否用二维的面积来解决呢？用如图9，利用线段比例关系可以得到面积关系：

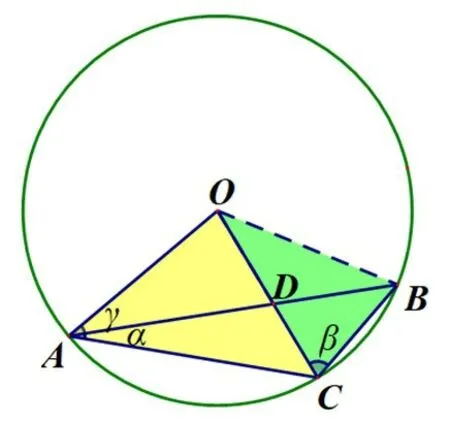
图9

S△AOD=2S△BOD，S△ACD=2S△BCD，两式相加发现S△AOC=2S△BOC，易得S△ABC=所以S△BOC=，利用面积公式或者作高，都能发现∠BOC=30°.

4 深度剖析

此题中，除了对解法进行赏析，对条件进行变形分析依旧可以发现另一番风味.

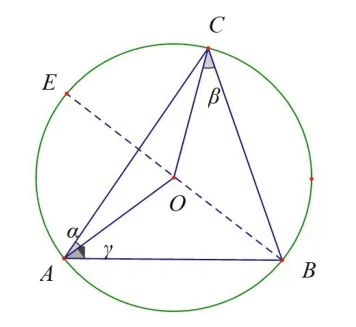
图10

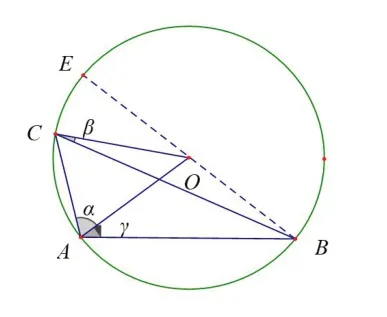
图11

思考2在∠ACB＞90°时，发现α+β=90°，那么在∠ACB＜90°时，这个数量关系依旧成立吗？通过分析发现，当点C在上运动时，α+β=90°恒成立；当点C在弧AE上运动时，α-β=90°恒成立；

思考3当∠ACB＜90°时，线段BD、CD，弧BC围成的图形面积S是否依旧能算？为了让∠AOC=90°这个数量关系依旧存在，发现β和γ应该满足的数量关系是β=45°-γ.当D点在AB的什么位置时，面积可以求得呢？令AD=nBD，为了让∠COB为特殊角，那么n可以取哪些值呢？发现n=1 时，∠COB=90°，此时C点位置很特殊，C在AB的中垂线上，但此时∠ACB=90°,与前提条件不符；另外，当n=时，∠COB=120°；n=时，∠COB=150°.这些特殊情况下都可以求得面积S.

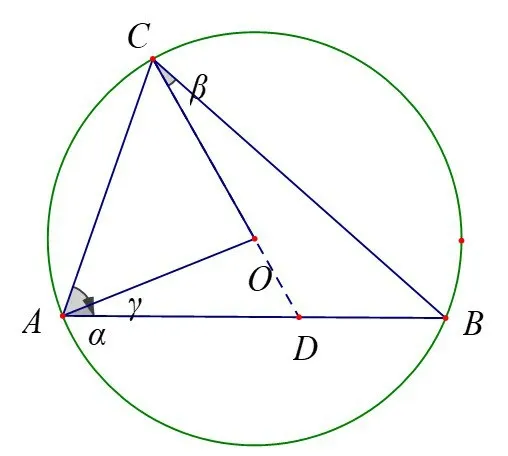
图12

5 反思

波利亚有句名言，“掌握数学就意味着善于解题”，解题能力的提升并不能简单地靠题海战术.我们要弄清楚题目的来龙去脉，会分析题目的条件，题中每个条件和结论都蕴含了出题者的心血，都是解题的突破口.在解题教学中，不满足于解出问题，更要学会分析问题，让学生沉浸于学习之中，激发学生深度思考，体会探索之快乐，培养学生的创新意识.