把握考题本质 促成深度教学——对2021年全国乙卷理科数学第11题的教学设想

安徽省涡阳第四中学 蒿广钦 王进喜 孙传彬 （邮编：233600）

《中国高考评价体系》中指出，高考必须坚持引导教学，高考有利于理顺教考关系，实现“以考促教、以考促学”的目的.不少试题体现了高考对教学的导向，有着重要的研究价值，如果将它们应用于教学，将对教学有良好的促进作用.对2021 年全国高考数学试题进行研究，发现全国乙卷理科数学第11 题是一个特别不错的题目，在此将对此题运用于教学的设想写出来，以期与同仁交流.

1 试题呈现

此题考查了椭圆与不等式等方面的知识，既注重了知识的基础性，又注重了综合性，它的基础性体现在解法上可运用解析几何中的坐标法，这是解析几何的灵魂；它的综合性体现在要运用椭圆、不等式和最值等方面的知识，具有较强的综合性.本题也较好地考查了学生在逻辑推理和数学运算等方面的数学核心素养，确实是一道很优秀的数学试题.

2 教学设想

本题作为一道很好的数学试题，可应用于课堂教学中去，以培养学生的探究意识.可从下面三个环节进行设计：

2.1 把握本质，直观感知

本题是以椭圆和不等式为背景，实质是关于椭圆上的点与定点的最大距离问题，教学时教师在黑板（或屏幕）上展示本题图形，记椭圆的下顶点为点D,右顶点为点A,让学生思考：如果不考虑|PB|≤2b，椭圆上与定点B的最大距离的点可能出现在哪里？由于椭圆的对称性，只考虑y轴及其右侧.学生会猜测到以下三种情形：（1）下顶点D处；（2）右顶点A处；（3）椭圆的第四象限部分的某点处.

教学估测第三种情形可能有的同学会忽略，教学时可以借助几何画板加以展示.

2.2 科学推证，寻求答案

在分析本题的解答时，教师主要从下面两方面加以引导：（1）|PB| ≤2b，由于2b是短轴的长，取等号时说明椭圆上与定点B的最大距离的点出现在下顶点D处；（2）椭圆上的点与定点B的距离属于两点距离的问题，因而此问题可以从两点间距离入手，由此学生就会联想到坐标法，设出椭圆上点P的坐标来.接下来学生去尝试，教师适时点拨.

教学估测（1）学生尝试时，可能会忽略y∈[-b,b]，造成解题障碍；（2）学生可能忽略二次函数的对称轴与单调性的关系来探求最值，造成解题障碍.

2.3 探究规律，深度教学

引导学生探究更一般的情形:已知椭圆C:=1(a＞b＞0)，点B(0，m)，其 中m≥0，点P椭圆C上任意一点，探讨何时椭圆上点P与定点B的距离最大？

学生先去尝试，师生共同总结.

由此可见，椭圆上与定点B的距离最远的点可能在椭圆的顶点处，也有可能在象限内，要具体问题具体分析，这取决于m、a和b的关系.

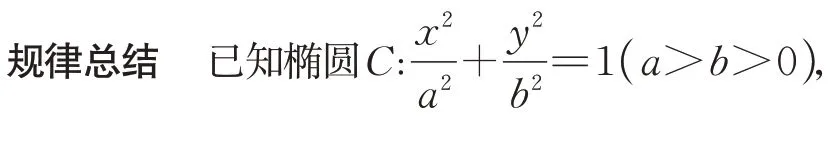
说明此题属于第二种情形.

3 几点思考

3.1 关注真题

高考题是命题专家精心打造的试题，体现命题者的智慧和心血，既能反映教学知识的重点，又能体现高考的命题原则；既能考查学生掌握的知识，又能考查学生的能力和素养.甚至一些问题在高考卷中反复考，常考常新，对高三迎考复习有很好的指导作用，因而复习课上可以借鉴往年的高考真题组织教学.比如今年全国乙卷文、理科数学第11 题反映的就是解析几何中的典型问题，即椭圆上的点与定点的最大距离问题，其实这个问题在往年的高考已经出现.1990 年全国理科数学试题：已知椭圆的中心是坐标原点，长轴在x轴上，离心率为已知点到这个椭圆上的点的最远距离是，求这个椭圆的方程，并求椭圆上到点P的距离是的点的坐标.

3.2 教师先行

教师要有研究高考真题的热情和习惯，每年高考之后，教师要迅速投入到对当年高考试题的研究之中，也可借助一些期刊杂志与同仁一起研究，教师只有先行研究，把高考题研究透彻，才能进行有效筛选，更好地应用于教学，发挥考题的潜在价值，加强高考复习的针对性和有效性.

在高考命题专家命题时，常常会对一些典型的问题进行具体化或某种情形，进行创编高考试题，比如2021 年全国乙卷文、理科数学第11 题分别是椭圆上的点与定点的最大距离问题的两种情形，这就要求教师在研究高考试题时进行深度探究，探求出一般规律，然后进行适当的教学设计，引导学生去探究，达到培养学生能力和发展学生数学素养的目的.

3.3 学生为本

在将高考试题运用于课堂教学时，教师要树立学生为本的教学理念，要严防教师唱独角戏，教师要授之以渔，通过问题的创设，引导学生步步逼近答案，让学生大胆地去想，大胆地去尝试，教师适时地做好帮扶，这样才能由教师的深度研究带来学生的深度学习，帮助学生寻找科学的研究方法和培养学生的科学探索精神，从而发挥考题的价值，提升数学复习的有效性，达到素质教育的目的.