追本溯源寻本质 拓展深化促素养——通过一道自主招生试题的解答与拓展过程感悟解题教学

安徽省岳西中学 刘建华 （邮编：246600）

安徽省合肥市第四中学 周赛龙 （邮编：230000）

《普通高中数学课程标准（2017 年版）》（以下简称“标准”）强调高中数学教学要以发展学生数学学科核心素养为导向,创设合适的教学情景,启发学生思考,引导学生把握数学内容的本质,促进学生实践能力和创新意识的发展[1].在中学数学课堂中,解题教学是常规的教学方式之一.著名数学家波利亚说过：“掌握数学就意味着善于解题”,作为一线数学教师,如何摆脱“题海战术”,使解题教学真正成为提升学生思维品质、提高学生数学素养的有效方式,是我们一直探索并思考的问题.本文,笔者就以“2016 年清华大学自主招生第26 题的解答与拓展过程”为例,阐述这方面的实践与感悟,旨在践行“标准”对发展学生数学思维,提高学生核心素养的育人要求.

1 提出问题，引发思考

2016 年清华大学自主招生第26 题是这样一道题：

原问题若O点为△ABC内一点,满足SΔAOB∶SΔBOC∶SΔCOA=4∶3∶2,设则λ+μ=____.

此题是一道背景内涵丰富、拓展空间广阔、育人价值突出的平面向量综合问题.但多数参考答案直接利用二级结论（奔驰定理）进行求解,不仅人为给高中学习与自主招生考试之间制造了一条难以逾越的“鸿沟”,更与“标准”所倡导的“重视基础、回归教材”的理念背道而驰,严重流失了题目背后丰富的知识内涵,育人价值难以体现.

2 追本溯源，回归基础

我们知道,平面向量基本定理是对向量线性运算几何形式、代数形式的抽象概括与统领,是解决向量问题的基础知识[2].根据题目的条件,我们可以考虑利用平面向量基本定理,以为基底表达和研究此问题.那么,解决问题的关键是利用SΔAOB∶SΔBOC∶SΔCOA=4∶3∶2,确定点O在ΔABC内部的具体位置.

解法1因为SΔAOB∶SΔBOC∶SΔCOA=4∶3∶2，

所以SΔAOB∶SΔABC=4∶9,SΔCOA∶SΔABC=2∶9，

结合O点为ΔABC内一点知：

点O既在与AB平行的线段DE上,又在与AC平行的线段FG上.

即：点O是DE与FG的交点，如图1所示.且DE∶AB=5∶9,FG∶AC=7∶9.

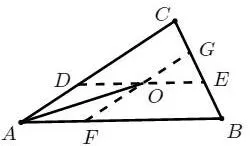
图1

另外,根据题目的条件背景,我们也容易联想到向量的典型问题模型：三角形重心的向量表示.即：如图2 所示,若O点为ΔABC重心,则有且SΔAOB∶SΔBOC∶SΔCOA∶SΔABC=1∶1∶1∶3.故也可尝试将问题转化为此基本模型进行解决.

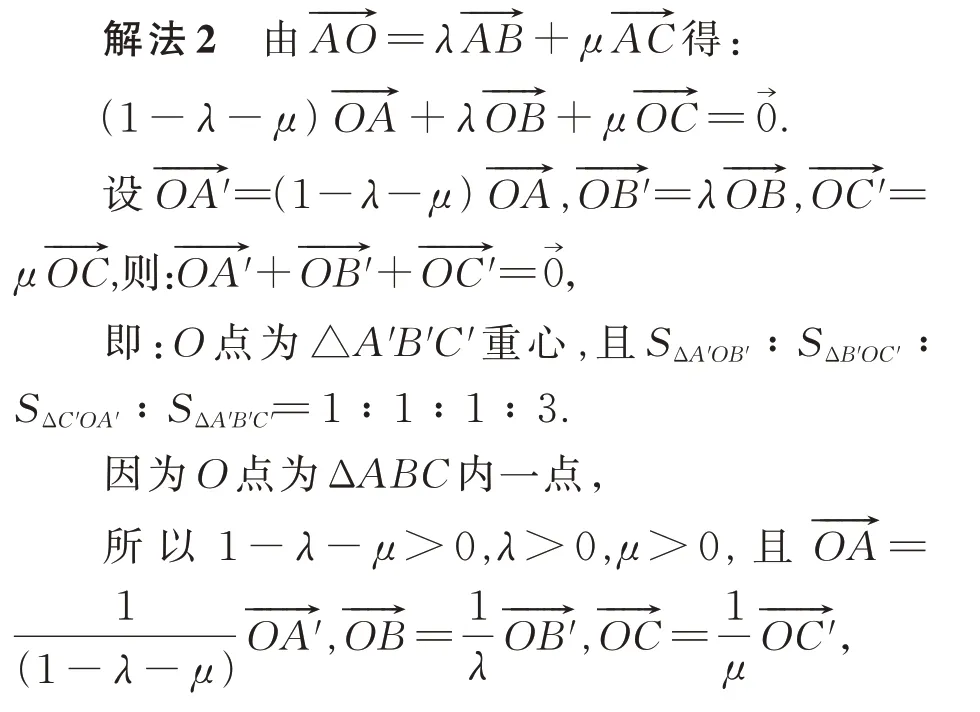
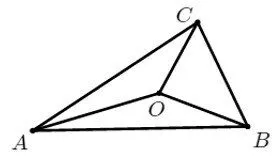
图2

评注解法1 利用基底法将问题回归到基本知识,解法2 利用图形构造法将问题转化为熟悉的基本问题模型,两种解法均利用平面向量“形”的特点,结合向量的几何意义,使问题的解答回归到数学的基础知识、基本思想及核心思维,体现了图形构造、转化化归等数学思想.

3 拓展深化，展开联想

3.1 初步拓展，揭示规律

我们知道,ΔABC三边所在直线可以把一个平面划分为7 个区域,如图3 所示.而原题目中限定O点为ΔABC内一点,其实只考虑了点O在I 区的情况,那么,当点O在其他区域时又是什么情况呢？为了揭示问题的一般规律,可以对原问题进行如下拓展探究：

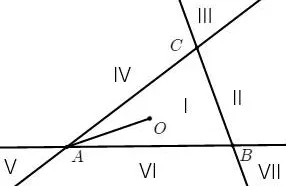
图3

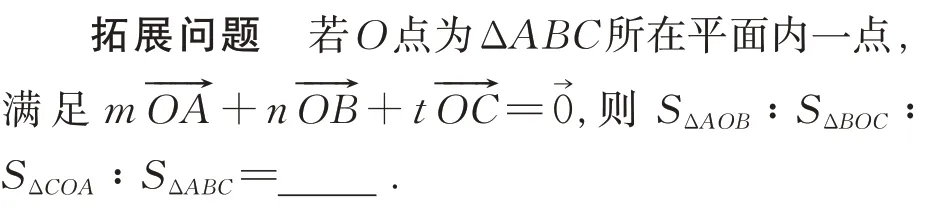
由于O点在平面内位置未知,且m、n、t的取值具有不确定性,所以,该拓展问题再想利用平面向量“形”的特点求解就会存在一定难度.不过,我们知道,平面向量除了具有“形”的特点外,还兼具“数”的特点.平面向量的坐标就是向量的代数表示,它可以使向量的运算完全代数化,是将某些复杂的几何问题转化为熟悉的数量运算的桥梁.因此,我们可以考虑使用向量坐标法来解决此问题.

解如图4 所示,以点A为坐标原点,边AB所在直线为x轴建立坐标系.则：A(0,0).

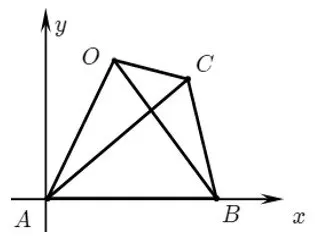
图4

设：B(xB,0),C(xC,yC),O(x,y),则：

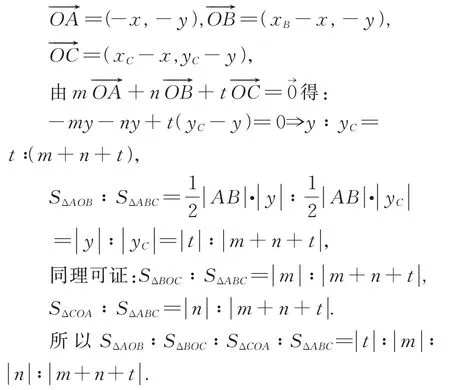
通过对拓展问题的探究与求解,最终揭示问题的一般规律：

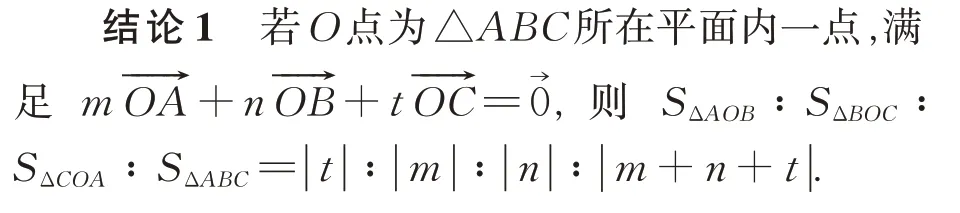
3.2 深入拓展，发散思维

在结论1 的基础上,我们又可以进一步思考：若O点是空间中一点,有没有与平面内类似的规律呢？即引导学生将结论1 由二维平面类比到三维空间得到并证明结论2：

结论2 的证明方法与结论1 类似,建立适当的空间直角坐标系,运用向量坐标法即可证之,可由学生自主独立完成,此处不再赘述.

评注一方面,平面向量是沟通代数、几何的有利工具,兼具“数”和“形”的特点.采用向量坐标法对问题进行求解,不仅将复杂的几何问题代数化,而且通过代数运算和代数式往往更容易发现问题的一般规律,如结论1、2 的发现.另一方面,结论1、2 是对原问题逐步拓展所生成的新收获,通过对问题的不断拓展深化,不仅可以加深学生对问题本质规律的理解与掌握,更能让学生的数学思维、核心素养都得到充分的发散与发展,是培养学生实践能力和创新意识的有效方式.另外,结论1 其实与奔驰定理本质相同,当O点在ΔABC内部时,SΔAOB∶SΔBOC∶SΔCOA∶SΔABC=t∶m∶n∶(m+n+t),将 式 子中的m、n、t用面积进行替换,即可得到奔驰定理由此可使学生感受到,大学自主招生也并非如此“高不可攀”,回归到中学的基础知识、基本思想方法,同样可以揭开自主招生试题的神秘面纱.

4 变式应用，体验收获

首先,为了体验原问题的一般性,不限定O点在ΔABC内部,对其做如下变式：

根据结论1 的问题模型可知：SΔAOB∶SΔBOC∶SΔCOA=|μ|∶|1-λ-μ|∶|λ|=4∶3∶2.

因此,变式问题可结合上图3 按区域进行分类求解,具体见下表1：

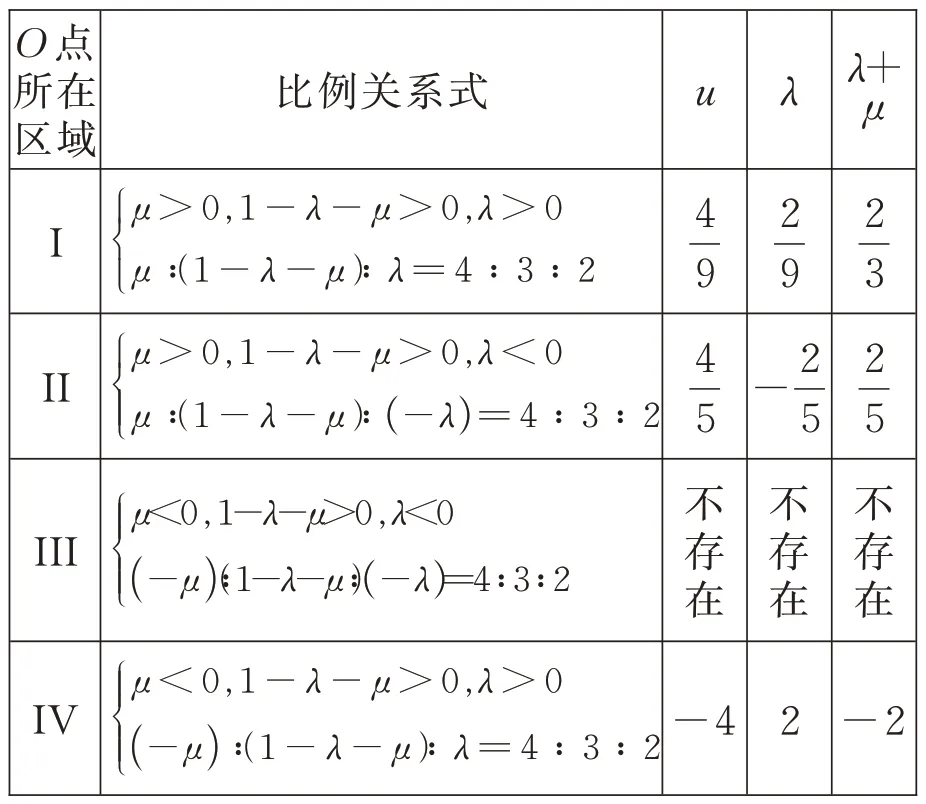
表1

μ ＜0,1-λ-μ ＜0,λ ＞0 V ■■■■■()-μ ∶(λ+μ-1)∶λ=4∶3∶2不存在__不存在__VI ■■_____■μ ＞0,1-λ-μ ＜0,λ ＞0 μ∶(λ+μ-1)∶λ=4∶3∶2 VII ■■■■μ ＞0,1-λ-μ ＜0,λ ＜0 μ∶(λ+μ-1)∶()-λ=4∶3∶2 4 3 _______________________________________________________________不存在2 3 不存在不存在 2 不存在

综上可知：λ+μ=或±2.

另外,为了体验原问题的发散性,不限定O点在平面内,对其做如下变式：

评注变式问题1、2 是对结论1、2 的巩固应用.对于变式问题1,点O在II～VII 区域本质上与在I 区的情况类似,所以,也可以鼓励学生继续利用平面向量“形”的特点,类比原问题的2 种解法来解决此问题.对于变式问题2,类似地,空间中三棱锥A-BCD的四个平面可以把空间分为15 个区域,点O除了在三棱锥A-BCD内部之外,在空间中的其他区域的情况又如何呢？这些想法的实践对学生数学能力、思维、素养的发展同样具有重要价值,可留给学生课下慢慢探究.另外,通过变式问题对结论的应用,不仅可以使学生体会到拓展探究、获得知识的价值与快乐,更能激发学生学习数学的激情以及创新、创造的信心.

5 总结反思 感悟启示

《怎样解题》中有这样一段话：“解决数学问题要善于联想——你以前见过它吗？你是否知道与此有关的问题？你是否知道一个可能用的上的定理？这里有一个与你现在的问题有联系且早已解决的问题,你能不能利用它？你能利用它的结果吗？你能利用它的方法吗？……[3]”根据以上启发并结合教学实践,笔者认为,在数学解题教学中,有效的解题探究过程大体会经历如下4 个阶段：

（1）明确问题,回归基础,寻找“依靠”.当学生面对一个问题毫无解题思路时,首先,必须理解该题目的语言陈述——未知量是什么？已知数据是什么？条件是什么？这样才能联系题目初步思考与问题相关的基础知识是什么？基本方法是什么？以此找到解决问题的基本“依靠”；

（2）联系问题,探求思路,确定解法.好的思路来源于过去的经验和以前获得的知识.在明确题目考察知识内容的基础上,可进一步思考与问题类似的基本问题模型是什么？这些问题间有什么区别和联系？依次考虑变化问题的不同方面,在脑海中不断地把它们转一遍又一遍,在变化问题的过程中,通过分解、重组题目元素,或者应用普遍化、特殊化、类比的丰富来源,筛选出有效解决问题的关键思路以及可行解法；

（3）反思问题,凝结归纳,深化理解.解题教学的目的不是让学生为了解题而“解题”,而是让学生通过解题而“学会解题”.因此,在解决问题后,教师要带领学生回顾完整的答案,重新斟酌、审查结果及导致结果的途径,深度反思解决此类问题的关键知识与基本思想,及时凝结出解决问题的核心思维和基本方法,这对学生厘清问题知识本质、深化数学思想理解、提高数学学习能力大有裨益；一个好的教师必须要使他的学生深刻认识到：没有一个题目是彻底完成的了.总还会有些事情可以做；在经过充分的研究和洞察后,我们可以将任何解题方法加以改进；而且无论如何,我们总可以深化我们对答案的理解[4]；

（4）拓展问题,揭示规律,发散思维.在学生已有问题解决的经验基础上,积极地开展思考与发现,大胆地进行创新与拓展,充分发挥学生学习过程中的主体地位,在系统构建知识体系的同时,形成深入思考的习惯、拓展探究的方法以及创新创造的信心.这不仅是促进学生深度学习、揭示问题的一般规律、充分发散学生思维的有效途径,更是提升学生思维品质、培养学生创新意识、发展学生核心素养的重要载体[5].

如此就要求,解题教学,一方面应努力纵向延伸,追溯问题本源、探寻知识本质,将学习与思考不断深入；另一方面也要积极横向拓展,揭示一般规律,发散数学思维,培养数学实践与创新意识.最终,在纵横贯通中,将“就题论题”经由“就题论法”上升到“就题论道”层面,使解题教学真正成为提升学生思维品质、促进学生素养提升的有效方式.另外,需要强调的是,在解题教学过程中,不一定每一次解题都要经历上述所有阶段,但是,就如波利亚所说：“一个专心的、认真的老师能拿出一个有意义但又不复杂的题目,去帮助学生发掘问题的各个方面,使得通过这道题,就好像一道门,把学生引入一个完整的理论领域.”有效的解题教学,一定是我们努力追求的方向.