2022 年大联考导数题的解法研究

新疆乌鲁木齐市第八中学 李昌成 车燕昭 （邮编：830002）

1 题目呈现

（2022 年八省联考第8 题）设a、b都是正数，e 为自然对数的底数，若aea+1+b＜blnb，则（）

A.ab＞e B.b＞ea+1

C.ab＜e D.b＜ea+1

学生普遍反映本题无从下手，很难建立题设与问题间的关系.根据2021 年全国高考乙卷第12 题的结构、命题点位、解题方法，考生有大概的思路：构造，再利用单调性作答，但是很难具体实施解题思路.

2 试题解答

解由aea+1+b＜blnb，得

提取公因式，得

对数运算，得

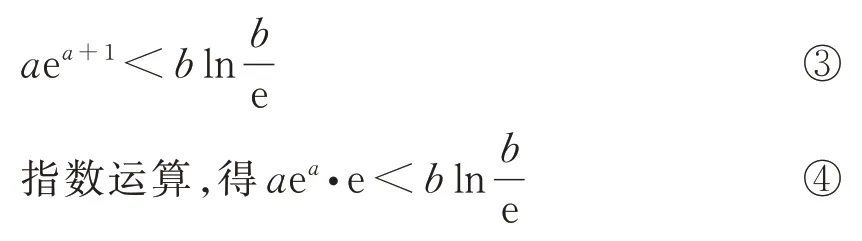
不等式两边同除以e，得

将a换成ln ea，得

构造函数f(x)=xlnx，得

因为a、b都是正数，

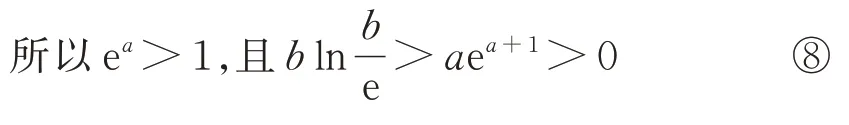
3 解答说明

考生之所以不能顺利完成解答，是因为对于以上每步解答的理由不清楚，或者是某一步不清楚，导致思路受阻.有必要把每一步理清，授之以渔.从参数分类的角度，a、b分别在不等式一端，执行了（1）；根据对数运算的需要，向熟悉的函数f(x)=xlnx靠近，提取了公因式，得到（2）；依托将常数1 转化为需要的对数ln e，以便执行对数运算（3）；从函数f(x)=xlnx的结构出发，需要将不等式左边的b转化为所以进行了（4）的指数式改装运算；（5）出现了函数f(x)=xlnx的雏形，需要关注不等式的右端的结构；对于第（6），必须有f(x)=xlnx的结构引领，熟知对数恒等式N=，否则无法执行此步；有了前六步的铺垫，（7）便应运而生；（8）（9）是为了应用f(x)=xlnx的单调性解题的准备步骤，弄清两个变量ea、所属范围，缺了此步，也将难以定夺选项.由此看来，命题专家对本题下了一番功夫，设置了多个构造环节，环环相扣.只有思维缜密的考生才能最终突围，具有很好的区分度，是名副其实的把关题.

本题还有其他构造方法，只是构造更加巧妙，对学生要求能力更高，尤其是等价转化的能力，抽象概括的能力！

另解1设φ(x)=xlnx-x，

则φ′(x)=lnx+1-1=lnx.

由前文知b＞e，所以φ′(x)＞0，

所以φ(x)=xlnx-x在(e,+∞)内单调递增.

又φ(ea+1)=ea+1ln ea+1-ea+1=(a+1)ea+1-ea+1=aea+1.

由aea+1+b＜blnb，得aea+1＜blnb-b，

所以φ(ea+1)＜φ(b)，所以b＞ea+1.

另解2设λ(x)=lnx+x（x＞0)，

则λ(x)在(0,+∞)内单调递增.

由aea+1+b＜blnb，a＞0，得

0 ＜aea+1＜blnb-b.

取自然对数，得lnaea+1＜ln [blnb-b]，

化简得lna+a+1 ＜ln(lnb-1)+lnb，

移项得lna+a＜ln(lnb-1)+(lnb-1)，

所以λ(a)＜λ(lnb-1)，因此a＜lnb-1，

解得b＞ea+1.

4 追根溯源

关于构造思想，教材在不同章节均有一些思想渗透，我们要深入领悟.就导数而言，在人教A版选修2-2[1]的第32 页安排了以下经典证明习题：

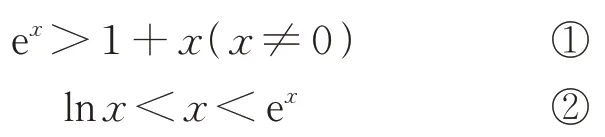
这两个习题给我们提供了学习构造法的平台，从代数的角度可以分别构造函数f(x)=exx-1(x≠0)，h(x)=lnx-x(x＞0)，g(x)=x-ex(x＞0)，

再利用这些函数的单调性证明不等式，也可以依托函数y=ex，y=1+x，y=x，y=lnx，在同一坐标系中，通过图象直观感知不等式的正确性.事实上，基于这两个不等式结构和条件，我们可以构造大量的不等式，例如：

（1）ex≥1+x（①式扩大定义域）

（2）ex-1＞x（将①中x换成1-x）

（3）e-x≤(x＞-1)（对①式取倒数）

（4）2 lnn＜n2（将②中x换成n2）

5 常见构造模式

（1）已知f′(x)g(x)+f(x)g′(x)＞0，构造函数h(x)=f(x)g(x).

理由h′(x)=f′(x)g(x)+f(x)g′(x)，能判断函数h′(x)的正负，可利用函数单调性解题.

理由h′(x)=ex[f(x)+f′(x)]，能判断h′(x)＞0，可利用函数单调性解题.

（8）已 知xf′(x)+f(x)＞0，构造函数h(x)=xf(x).

理由h′(x)=f(x)+xf′(x)，能判断h′(x)的正负，可利用函数单调性解题.

（9）已 知xf′(x)+nf(x)＞0，构造函数h(x)=xn f(x).

理由h′(x)=xn-1[nf(x)+xf′(x)]，能判断h′(x)的正负，可利用函数单调性解题.

显然，以上条件不等式中不等号变为小于号，不影响函数构造.

6 高考链接

例1[2](2021 年普通高等学校招生全国统一考试理科数学(乙卷)第12 题) 已知a=2 ln 1.01，b=ln 1.02，c=-1，则（）

A.a＜b＜cB.b＜c＜a

C.b＜c＜aD.c＜a＜b

解记f(x)=2 ln(1+x)，g(x)=ln(1+2x)，h(x)=

于是f(0)=0，g(0)=0，h(0)=0，f(0.01)=a，g(0.01)=b，h(0.01)=c.

分别求导得

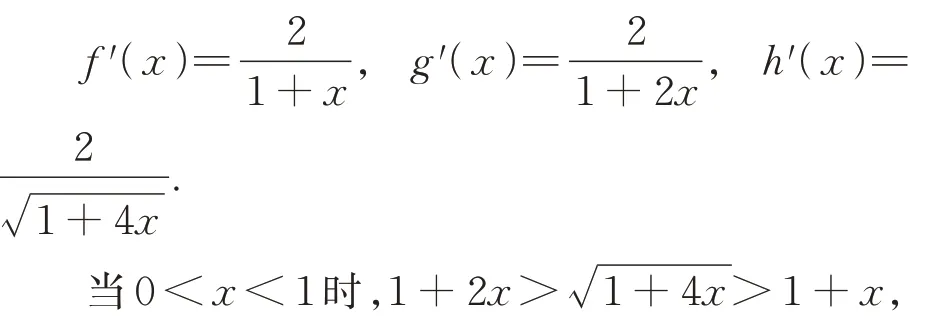
所以g′(x)＜h′(x)＜f′(x)，

结合导数的几何意义，得b＜c＜a.

因此选B.

例2[3](2015 年全国高考Ⅱ卷理科第12 题）设函数f′(x)是奇函数f(x)（x∈R）的导函数，f(-1)=0，当x＞0 时，xf′(x)-f(x)＜0，则使得f（x）＞0 成立的x的取值范围是（）

A.(-∞,-1)⋃(0,1)

B.(-1,0)⋃(1,+∞)

C.(-∞,-1)⋃(-1,0)

D.(0,1)⋃(1,+∞)

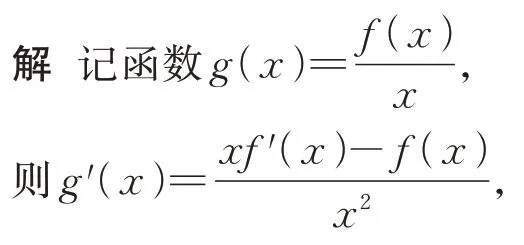
因为当x＞0 时，xf′(x)-f(x)＜0，

故当x＞0 时，g′(x)＜0，

所以g(x)在(0,+∞)内单调递减；

又因为函数f(x)（x∈R）是奇函数，

故函数g(x)是偶函数，

所以g(x)在(-∞,0)内单调递增，

又g(-1)=g(1)=0.

当0 ＜x＜1 时，g(x)＞0，则f(x)＞0；

当x＜-1 时，g(x)＜0，则f(x)＞0.

综上所述，使得f(x)＞0 成立的x的取值范围是(-∞,-1)⋃(0,1).

故选A.

7 牛刀小试

（1）(原创）设函数f(x)（x∈R）的导函数是f′(x)，f′(x)-f(x)＞0，则（）

A.ef(2021)＜f(2022)

B.ef(2021)＞f(2022)

C.f(2021)＜ef(2022)

D.f(2021)＞ef(2022)

参考答案：A.

（2）(原创）设正实数a、x，使得不等式aeax≥lnx，则（）

A.a≥e B.a≤e

C.a≥e-1D.a≤e-1

参考答案：C.