柔直换流阀损耗解析计算及其误差分析
2022-04-26李标俊向权舟姚传涛余琼
李标俊,向权舟,姚传涛,余琼
(1. 中国南方电网有限责任公司超高压输电公司天生桥局,贵州 兴义 5624002;2. 荣信汇科电气股份有限公司,辽宁 鞍山 114051)
0 引言
近年来,基于模块化多电平换流器(modular multilevel converter,MMC)的柔直换流阀因具有运行效率高、输出特性好、可拓展性强等优点,成为柔性直流输电系统换流阀的首选方案[1-3]。换流阀损耗作为系统重要的性能及经济评价指标,直接关系到能量损耗和运行成本[4-8]。
目前,关于功率器件的损耗计算、优化方法比较多,总体上经历了完善通用损耗计算方法、提升计算结果精度、提出损耗优化等过程[9-10]。文献[11-14]将换流阀调制方式等效为理想的正弦脉宽(SPWM)方式,推导了损耗计算解析表达式,适用工程初期损耗快速评估和功率器件初步选型。文献[15-16]从调制策略角度对全桥功率模块的器件损耗进行了优化和平衡。文献[17-19]从结温反馈、结温预估和实时结温探测等角度对损耗结果进行修正。上述解析法仅仅给出中间结果,受限于求解过程复杂,没有得出覆盖影响损耗结果的完整表达式。在实际工程中,模块化多电平换流器(MMC)换流阀采用电平逼近调制策略,器件开关时序在一定时间内存在较大随机性。文献[20]基于仿真的损耗计算方法,从仿真波形中提取器件的导通及开关序列,结合运行工况及器件参数计算器件损耗,但仿真波形与实际工程现场波形存在的差别会对计算结果精度产生影响。
本文首先在现有损耗计算解析方法基础上,通过精确求解,得到可覆盖系统运行工况和器件特性参数的通用解析表达式。将解析式中每个影响损耗的参数定义为损耗影响因子,分别分析逆变工况和整流工况损耗影响因子的权重及其对损耗计算结果的影响程度,从而为后续优化换流阀损耗提供依据。通过提取实际的开关序列波形,详细对比与脉宽调制方式器件投切时序及开关频率的差异,由此分析损耗计算误差来源。更进一步,提出基于工程现场实际录波数据的损耗计算方法。最后,以某工程现场为案例,进行仿真验证。
1 损耗解析计算法
功率器件损耗受系统运行工况和器件特性影响较大,是换流阀损耗计算的难点[21]。MMC功率模块的运行工况可根据平均开关模型等效为相同开关频率的SPWM调制模式,得到统一公式。
1.1 功率模块等效SPWM调制原理
半桥功率模块拓扑结构原理如图1所示。图中:T1、T2为绝缘栅双极型晶体管(IGBT);D1、D2为反并联二极管;C为直流电容;R为放电电阻;S1为旁路开关。本文设电容容值、电压分别为uC,单元两端的电压、电流分别为uSM、iSM。

图1 半桥功率模块拓扑结构Fig. 1 Topology of half-bridge power module
将换流阀电压平均至每个功率模块,则uSM、iSM为
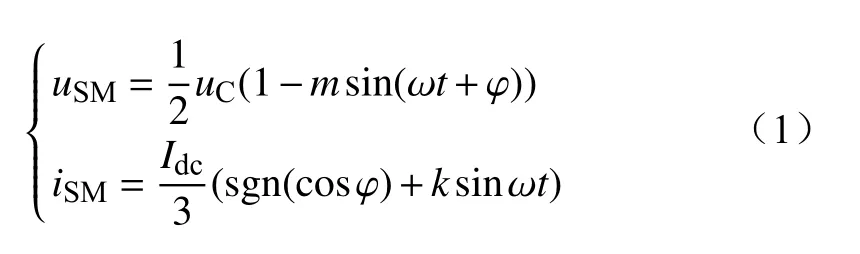
式中:m为换流阀电压调制比;ω为角频率;t为时间;Idc为换流阀电流直流分量;k为换流阀电流交流分量与直流分量之比;为功率因数角。
将功率模块调制方式等效为SPWM调制,按照上式得到调制原理及波形如图2所示。

图2 SPWM调制波及载波Fig. 2 SPWM modulated waveform and carrier waveform
设第k个脉冲的占空比为Dk,即

不难分析,当iSM>0时,D1和T2轮流导通;当iSM<0时,T1和D2轮流导通。设T1、T2、D1、D2在一个开关周期TC内导通时间分别为tT1、tT2、tD1、tD2,能够分析得出
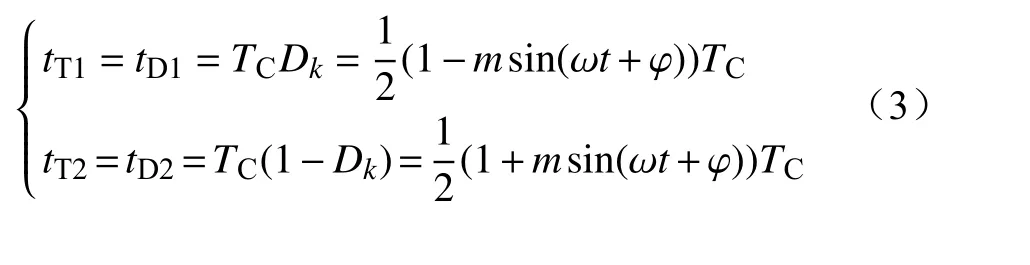
当输出有功不为零时,iSM含直流分量,为不对称波形。根据电流表达式,当系统为逆变工况时,计算得到iSM<0的功率因数角区间为[φ1,π–φ1],iSM>0的功率因数角区间为 [π–φ1,φ1+2π];当系统为整流模式时,与逆变呈对偶性,iSM<0的功率因数角区间为 [φ1,π–φ1],iSM>0的功率因数角区间为 [π–φ1,φ1+2π]。其中,φ1=–arcsin(1/k)。
经过推导,得到平均导通时间为

进一步分析,当系统工作在逆变工况时,T2导通时间最长,D2导通时间最短;当系统工作在整流模式时, D2导通时间最长,T2导通时间最短。
1.2 功率模块损耗解析计算方法
功率器件的导通损耗uF为

式中:rT为器件斜率电阻;UTO为器件等效阈值电压;iF为二极管导通电流。
结合各个器件的导通时间,以积分方式求解每个器件的导通损耗,以逆变工况为例,整理得到的解析表达式为

式中:io为桥臂电流有效值;Io为桥臂电流交流分量;Ic为桥臂电流峰值;k'为k的倒数;ro、uo分别为IGBT的斜率电阻和等效阈值电压;rdo、udo分别为二极管的斜率电阻和等效阈值电压;PT1-c、PT2-c、PD1-c、PD2-c分别为逆变工况下T1、T2、D1、D2的导通损耗。
根据不同器件的工作时间,可计算各器件在理想SPWM调制方式下的开关损耗为

式中:Ud为二极管实际电压;Unom为额定运行电压;fsw为功率模块的开关频率;PT1-s、PT2-s、PD1-s、PD2-s分别为 T1、T2、D1、D2的开关损耗;a、b、c分别为IGBT开关损耗的二次曲线拟合系数;ad、bd、cd分别为IGBT开关损耗和二极管开关损耗的二次曲线拟合系数。
2 损耗影响因子分析
本文定义影响功率模块损耗的参数为损耗影响因子,包括:传输功率、电压调制比、IGBT斜率电阻等。
影响因子的权重η为

式中:ΔP为损耗增比;Δλ因子增比。
影响因子权重越大,说明该参数变化对损耗影响越大。以某一已投运工程为例,分析各影响因子权重,参数如表1所示。
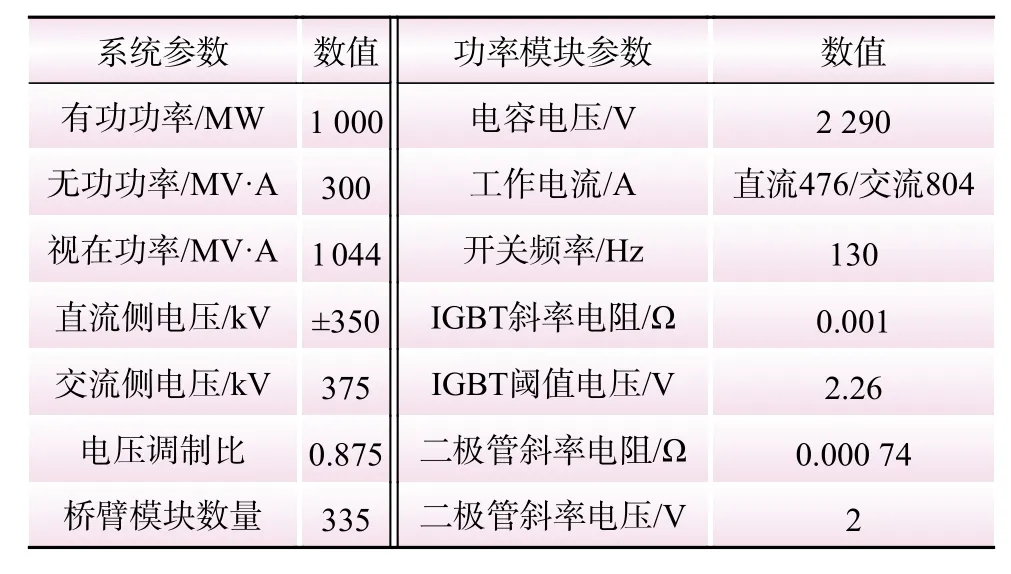
表1 系统工况和参数Table 1 Conditions and parameters of system
针对每个损耗因子,设定其增比为0.6~1.2,步进为0.1,分别与之对应的损耗增比,结果如图3所示。除传输功率之外,在逆变工况下,权重最高的损耗影响因子依次为开关频率、电容电压、IGBT阈值电压和斜率电阻,以1.2增比倍数为例,权重依次为0.37、0.31、0.29、0.24。
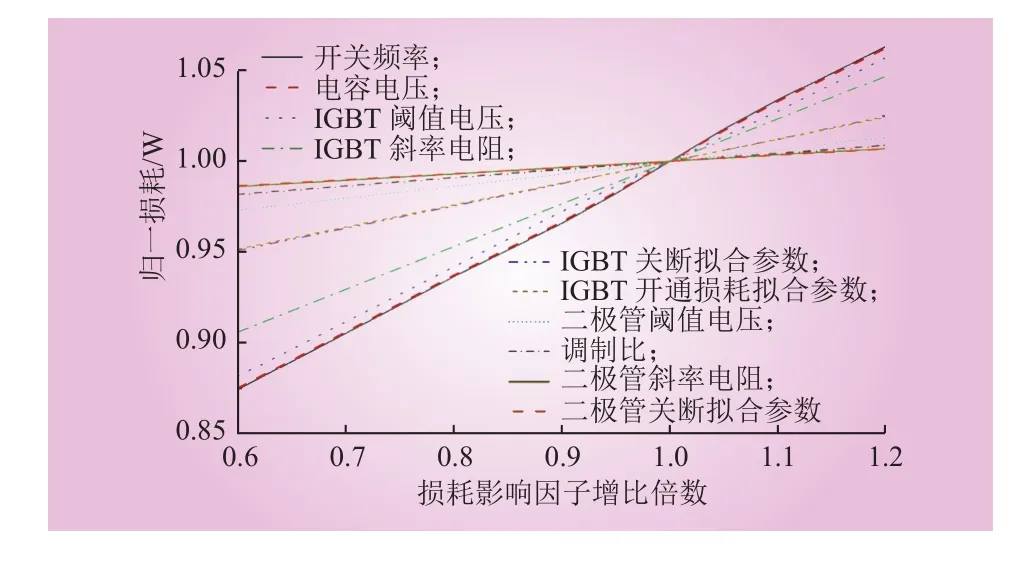
图3 逆变工况下损耗因子权重分析结果Fig. 3 Results of loss factor weight analysis in inverter condition
整流工况下损耗因子权重分析结果如图4所示。在整流工况下,最高的影响因子依次为开关频率、电容电压、二极管阈值电压和斜率电阻。因此,在工程设计阶段,可结合换流阀工况对权重较大的开关频率和器件饱和压降进行针对性优化,实现换流阀高效降损。
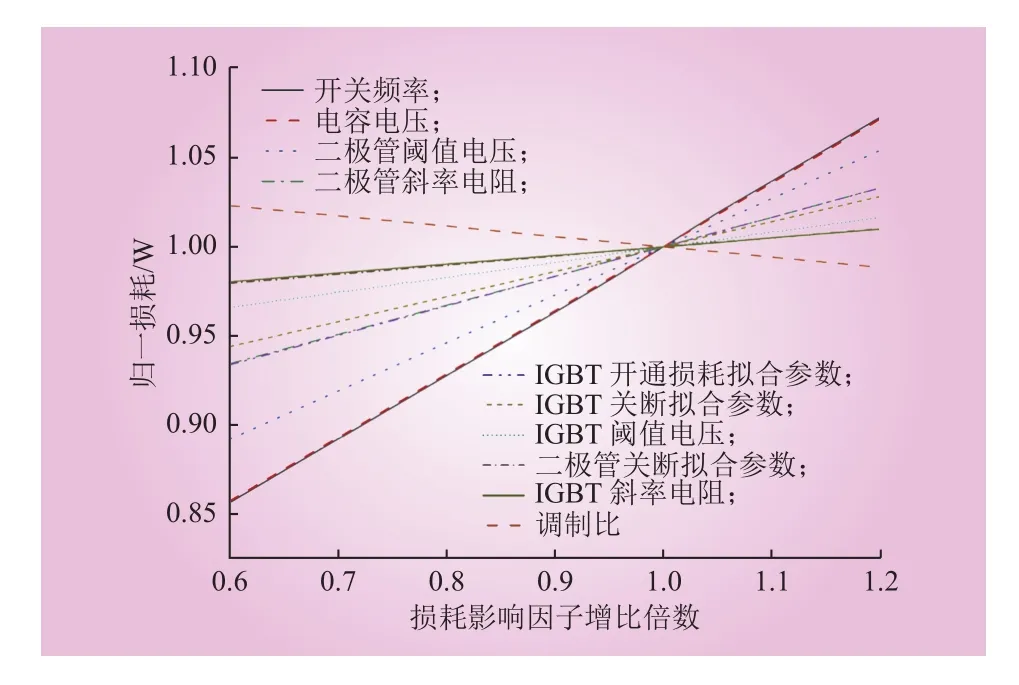
图4 整流工况下损耗因子权重分析结果Fig. 4 Results of loss factor weight in rectifier condition
3 损耗波形计算法及误差分析
实际工程中,柔直换流阀广泛采用基于电容电压平衡排序的最近电平调制算法[22-25]。与SPWM调制方法不同,电平逼近算法无法根据调制机理推导统一的解析表达式进行损耗计算。
以表1所示的实际工程为例,本文采用波形法对所获录波数据进行分析,得到的一组二极管D2典型导通及关断时刻电流波形,如图5所示。

图5 器件导通电流及关断时刻电流脉冲波形Fig. 5 Conduction current and turn off current pulse waveforms of device
此时,功率器件的导通损耗Pcon仍可由获取的器件导通电流和管压降乘积表示为
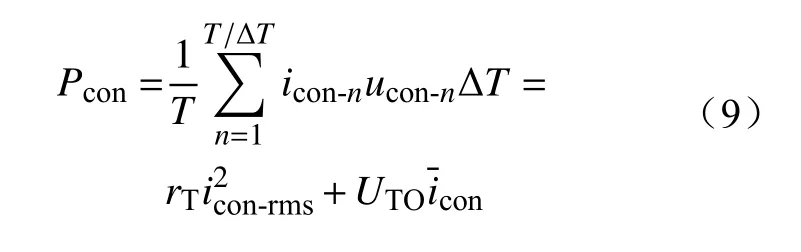
式中:UTO为IGBT阈值电压;ΔT为录波波形步长;T为计算周期;icon-n、ucon-n为时刻n器件导通电流及管压降;icon-rms、为器件导通电流有效值和导通电流平均值。
功率器件开关损耗Psw为

式中:Iswi-n、uswi-n分别为器件开关时刻n的电流及电容电压。
通过波形法计算得到的频率相关损耗与前文解析法计算结果进行对比,如图6所示。
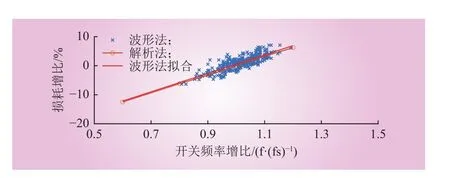
图6 功率模块损耗计算结果对比Fig. 6 Comparison of power loss Calculating results
在一定范围内,波形法与解析法计算得到的损耗增比差异在2%左右,波形法与解析法得到的开关频率损耗因子权重也存在一定差异。
考虑到调制策略不同对开关逻辑的影响,首先对器件开关时刻的电流绝对值分布进行统计分析。将电流在0~1 p.u.之内等分5个区间,记录开关电流落入每个区间的频次并计算对应占比,结果如图7所示。解析法在0.8~1 p.u.内占比比波形法开关频次要高5%左右,意味着解析法更大概率在大电流下开关和具有更大的开关损耗。

图7 解析法与波形法不同电流区间开关频次占比对比Fig. 7 Comparison of switch times between analytical method and waveform method in different current intervals
波形法不同功率模块器件损耗对比如图8所示。由图8可知,D2损耗最大,说明换流阀此时工作在整流工况。15个模块损耗平均值为3.15 kW,最大值为 3.25 kW,最小值为 3.06 kW。
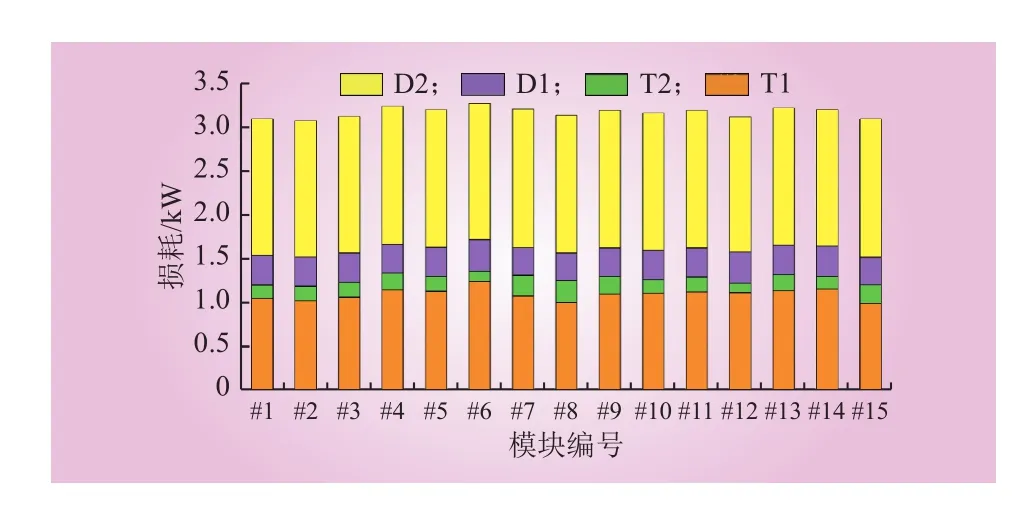
图8 波形法不同功率模块器件损耗差异对比Fig. 8 Comparison of device losses of different power modules by waveform method
解析法计算得到功率模块损耗为3.52 kW,比波形法高出0.37 kW,误差为11.7%,二者的损耗差异如图9所示。4个器件导通损耗非常接近,波形法和解析法分别为2.22 kW和2.30 kW。开关损耗差异较大,分别为0.94 kW和1.22 kW,说明2种损耗计算方法误差来源主要是开关损耗。

图9 波形计算法与解析法损耗结果对比Fig. 9 Comparison of loss results between waveform calculation method and analytical method
由以上分析可知,在确定柔直换流阀系统必要参数的情况下,解析法可以对系统损耗进行直接计算,易于得到分析结果,但不易发现系统各个模块中存在的与频率、电压相关的问题。波形法可以有助于发现解析法等效计算所滤除的功率模块细节问题,但每次计算前都需要从录波设备得到录波数据,并对大量波形进行处理之后得到分析结果,数据处理周期较长。
4 结论
本文在现有柔直换流阀损耗解析计算基础上,进一步通过理论推导得出可覆盖系统运行工况和器件特性参数的损耗解析式,对损耗因子的权重进行了分析。在逆变工况下,开关频率和IGBT的导通特性参数权重最大;在整流模式下,开关频率和二极管的导通特性参数权重最大,可以对换流阀损耗进行针对性的优化。针对解析法开关时序与实际工况不符的问题,提出基于工程现场录波波形的损耗计算法,综合来看,本文提出的解析法适用于工程前期损耗的快速评估和专项优化,波形计算法适用于工程投运之后损耗精确计算和评估。
