电力信息物理系统入侵容忍能力评估方法

姚鹏超，颜秉晶，郝唯杰，杨强

(浙江大学 电气工程学院，浙江 杭州 310027)

0 引言

随着信息通信技术的发展，传统电力系统的物理电气设备逐渐与网络设备(如控制、监控、计算和通信设备)相结合，逐渐演化为电力信息物理系统（cyber-physical power system, CPPS）[1]。因此，来自信息网络的攻击正在不断对CPPS造成新的威胁与挑战，与常规仅仅停留在信息层面的网络攻击不同，对CPPS的网络攻击可能会对工业控制系统的物理过程造成破坏，导致工业过程停工或严重的伤亡事故[2-3]。例如，2015年攻击者使用恶意邮箱攻击乌克兰电网控制中心，植入BlackEnergy病毒，配合DDOS攻击导致乌克兰电网大规模停电[4-5]。CPPS遭受网络攻击时的后果往往达到灾难级别，目前对于CPPS遭受网络攻击时的入侵容忍能力要求越来越高。

在CPPS网络安全问题越来越突出的情况下，建立一种针对CPPS的网络可靠性模型以评估CPPS的入侵容忍能力，并据此建立有效的防御体系是降低网络攻击影响的关键手段[6-7]。针对CPPS的信息物理融合的可靠性建模方法，国内外已做了很多相关工作。文献[8]从研究对象演化和研究方法层面对CPPS的可靠性评估研究展开综述，提出了信息物理融合视角下CPPS可靠性评估的研究思路和关键问题。文献[9]建立了一种电力-信息交互模型，探究电力信息物理系统交互机理及其对可靠性评估带来的影响。文献[10]主要考虑在信息失效威胁条件下的CPPS可靠性评估方法。文献[11]提出了一种将CPPS物理特性和信息流性能耦合在一个两层模型中的复合马尔可夫模型，在流量层面评估电力系统的可靠性。文献[12]提出了一种考虑最优防御资源配置的电力系统可靠性网络安全保险模型，将CPPS的可靠性以保险的形式报价评估。文献[13]基于蒙特卡洛方法，对信息系统和物理系统的可靠性进行评价并建立可靠性评估测试系统，分析了网络故障对可靠性的影响。文献[14]建立一种可靠性模型以捕获来自物理和信息组件的损害并评估组件之间的信息物理相互依赖的影响。

现有的CPPS可靠性评估方法存在简化甚至缺少信息层面的建模过程的问题，在可靠性分析中很少涉及网络空间模型的细节[15-18]。本文提出了一种CPPS入侵容忍能力评估方法，以半马尔可夫链（semi-markov chain，SMC）[12]为基础对高级可持续威胁（APT）攻击进行建模，具体分析来自网络层面的攻击对CPPS的破坏渗透过程。并利用随机博弈理论模型动态描述CPPS中攻防双方的交互过程，预测纳什均衡下攻击者的最优进攻策略，确定应对恶意攻击的最佳防御策略。最后以某CPPS安全试验场为例仿真验证了入侵容忍能力评估方法的有效性。本工作有如下创新贡献。

（1）为深入细致地描述来自网络层面的攻击对CPPS的渗透过程，本文以网络攻击中的APT攻击链为基础构建半马尔可夫链模型，具体详细地刻画APT攻击的每一阶段。

（2）以随机博弈为基础动态描述CPPS中攻防双方的交互过程，采用强化学习算法求解纳什均衡，预测攻击者在APT攻击中的最优进攻策略，制定最优防御策略。

（3）提出了一种CPPS入侵容忍能力评估方法，在有限防御资源条件下提出了一种最优资源分配方案，为高可靠性CPPS网络的防御机制设计提供一定借鉴。

1 CPPS网络架构与渗透模型

典型的电力工业控制系统具有明显的分层结构，可分为网络层与物理层，网络层又自上而下分为办公网络、生产管理网络、生产控制网络[19]。以图1 的CPPS安全试验场网络架构为例，其办公网络包含Web服务器、办公自动化（office automation,OA）服务器、邮箱服务器等设备，主要功能为提供Web服务、办公自动化与邮箱服务。生产管理网络包含生产控制站、设备管理站等设备，主要功能为自动化管理控制过程与设备。生产控制网络包含工程师站、操作员站等设备，主要功能为组态开发以及通过控制协议与控制器的直接通信。物理层包括由传感设备、控制设备、执行设备等设备组成的物理网络，其基于微缩装置模拟了大型火力发电场景：通过燃烧煤加热水，形成水蒸气给锅炉加压，增加的空气压力使阀门打开排气，推动电机旋转发电。

图1 CPPS安全试验场网络架构Fig. 1 The network architecture for a CPPS Testbed

由于电力工业控制系统不同网络之间存在网络隔离与防火墙规则限制，攻击者想要破坏电力系统的物理过程，一般需要从办公网络发动攻击并逐步渗透直至取得主机权限。如图2所示，攻击者首先需要利用漏洞攻击办公层的Web服务器等设备获取内部局域网的权限，再依次渗透至生产管理网络与生产控制网络，最后对电力系统的物理运行过程进行破坏。

图2 网络渗透模型Fig. 2 The cyber penetration model

传统的IT领域一般只考虑通信和计算机的安全问题，即图2中的网络层，然而，网络攻击一旦渗透到物理层，就会对电力系统造成巨大的破坏。因此为提高CPPS的入侵容忍能力，需要对来自网络层的攻击给予更多的重视。

2 CPPS入侵容忍能力模型

2.1 半马尔科夫链模型

攻击者持续渗透攻击CPPS的过程中，会经历多个进攻阶段， APT攻击链模型中将网络攻击分为信息侦查、武器构建、载荷攻击、漏洞利用、安装植入、命令控制6个阶段，其中关键在于发现并利用主机上存在的漏洞[20]。在攻击者渗透攻击的过程中，防御者也会进行入侵检测，装备入侵检测系统（intrusion detection system，IDS）、防火墙等防御设施，修复自身存在的漏洞来抵御攻击。

以APT攻击链模型为基础，本节采用半马尔科夫链模型对CPPS的攻击入侵过程进行建模，评估CPPS的入侵容忍能力。图3描绘了由一系列状态组成的网络攻击入侵过程，状态集可以表示为其中为转移状态，为吸收状态，描述如表1所示。

表1 SMC状态描述Table 1 The state description of SMC

图4描述了SMC模型中攻击者发动APT攻击的详细流程，右侧表示当前流程在图3中所对应的状态。APT攻击链的一次攻击过程可以描述为〈∗→ Ci→ Vi→ Hi〉，分别代表着从初始状态进行信息侦查、武器构建进入到内网，到载荷攻击、漏洞利用，再到安装植入、命令控制从而获得主机权限。攻击者的最终目的是对CPPS的物理过程进行破坏，一般需要完整进行4次APT攻击才能进入到物理网络并进行破坏。

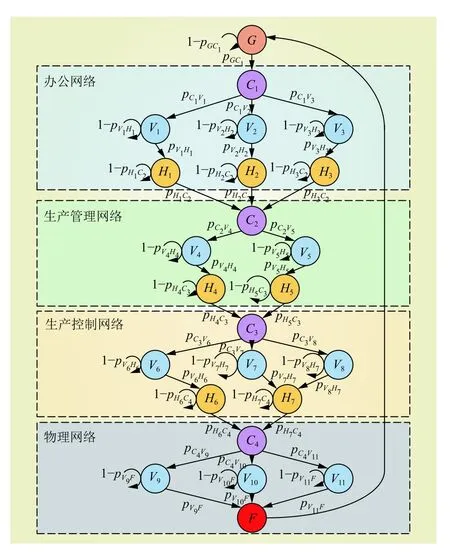
图3 半马尔科夫链APT攻击模型Fig. 3 The SMC model of APT attack

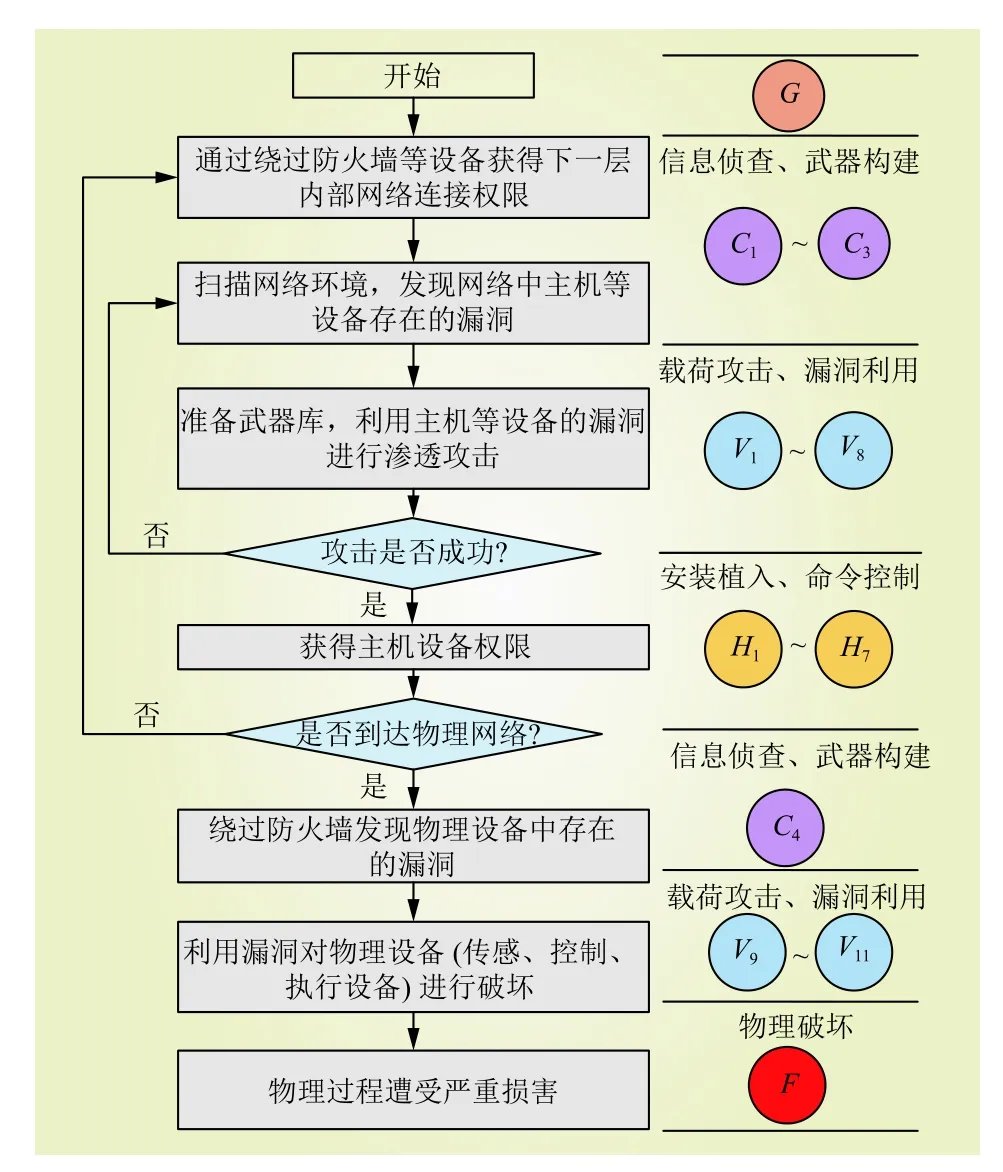
图4 APT攻击流程示意Fig. 4 The diagram of APT attack process

在本文中，基于APT攻击链的SMC模型共有23个状态，图3中同样说明了不同状态之间相应的转移概率，定义转移概率矩阵，大小为23×23，用于描述不同状态之间的转换关系，为矩阵中第列第行的元素，满足

表2 SMC转移概率Table 2 The transition probability of SMC

2.2 CPPS入侵容忍能力量化评估

将CPPS遭受APT攻击并最终物理发电过程遭受破坏的持续时间表示为CPPS的平均失效时间，以评估CPPS的入侵容忍能力[12]。在整个渗透攻击过程中，攻击者在每一个转移状态上都可能会停留数次，将定义为在转移状态上的停留次数，为在状态上的平均停留时间，其值根据试验场实际攻防演练时在每一状态的平均花费时间经验值得到。计算方法为

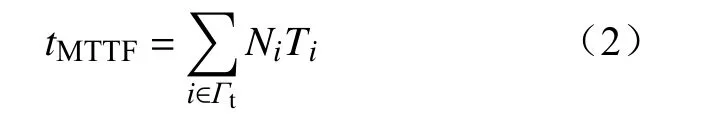
其中停留次数遵循关系为

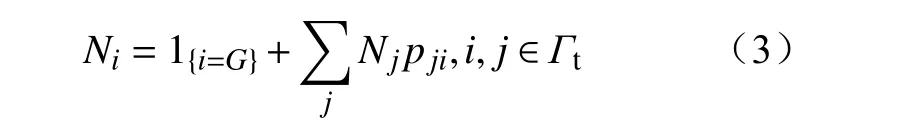
CPPS的可靠度是指从CPPS开始正常运行至某一时刻t 这段时间内正常运行的概率，用表示。可靠度可由CPPS的故障率计算[21]得到

3 基于随机博弈的攻击预测

3.1 随机博弈预测模型

随机博弈是由一系列状态组成的多个参与者进行的具有状态概率转移的动态博弈，在每一状态下，参与者可以从动作集中选择不同的动作，并获得取决于当前状态与行动的收益[22]。每一状态的博弈过程可以分解为矩阵博弈，并根据动作概率分布转移到下一状态。假定攻防双方的目的都是为了取得最大化的收益，即均为绝对理性。本节采用随机博弈模型来预测求解攻击方在进行APT攻击时的最优策略，以及防御方在防御时的最优防御策略[23]。

CPPS遭受攻击者破坏物理过程需要成功进行4次APT攻击，划分4次博弈状态 S ={S1,S2,S3,S4}，分别代表在办公网络、生产管理网络、生产控制网络、物理网络中攻防交互过程。博弈攻防双方分别表示攻击者与防御者，攻防双方动作集为代表攻防双方动作的策略集合即选择动作的概率分布；分别代表攻防双方动作花费时间集合；与分别代表攻防双方的效益函数。CPPS的随机博弈模型为G=

3.2 基于强化学习的博弈求解方法

在CPPS中，攻击者和防御者彼此没有对方完整的信息，本文选择采用强化学习的算法来求解博弈的纳什均衡策略。因为该场景中涉及2个智能体，所以在此采用minimax极大极小方法和-learning相结合的minimax-算法[25-26]。首先，minimax-采用极大极小法，通过线性规划求解每个特定状态的矩阵博弈的纳什均衡策略，最后运用-learning方法迭代学习状态值和最优策略。状态时攻击者的状态值定义为

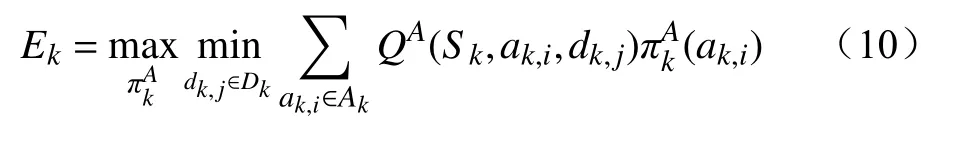
这意味着攻击者在与防守者的博弈中最大化了最坏情况下的期望收益，式（10）可用线性规划来计算矩阵博弈的纳什均衡解。

3.3 攻击预测

表3 矩阵博弈Table 3 The matrix game

其中，当攻击成功时攻击者会得到W1～ W4的正收益，根据矩阵博弈可预测求解攻击者在APT攻击初始阶段的使用不同攻击手段的概率分布{α1,α2,α3}。则防御者在网络边界处部署不同的防御设备时的概率分布为

4 实验设计与算例验证

本节以CPPS安全试验场为例，验证入侵容忍能力评估与防御资源最优配置方法的有效性。

4.1 实验参数

CPPS安全试验场模拟了真实场景下自上而下的工业控制系统控制过程。攻击者试图通过办公网络逐步渗透至工控系统，操纵传感器或是控制器来破坏火力发电过程。防御者对设备上的漏洞进行修补防止攻击者渗透利用，并在网络边界处安装防火墙或入侵检测系统来防御攻击者入侵。试验场具有开展网络攻防渗透测试的功能，因此本节将基于实际网络测试的结果进行仿真实验。

表4描述了CPPS安全试验场上设备的漏洞信息, 并给出了通用漏洞披露（common vulnerabilities& exposures，CVE）漏洞编号及成功利用后系统所需恢复时间。和的攻防行为如表5所示，并且描述了采取相应行为所需要的时间成本。半马尔科夫链中每一状态的为

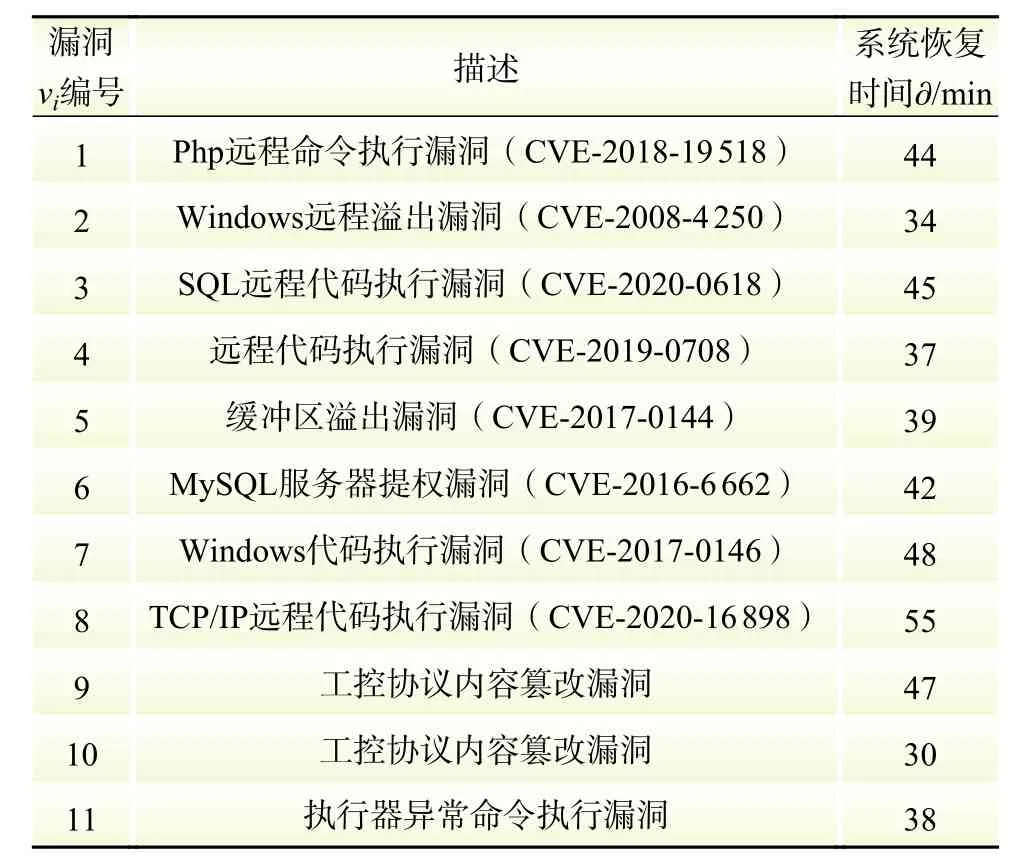
表4 漏洞信息Table 4 The information of vulnerabilities

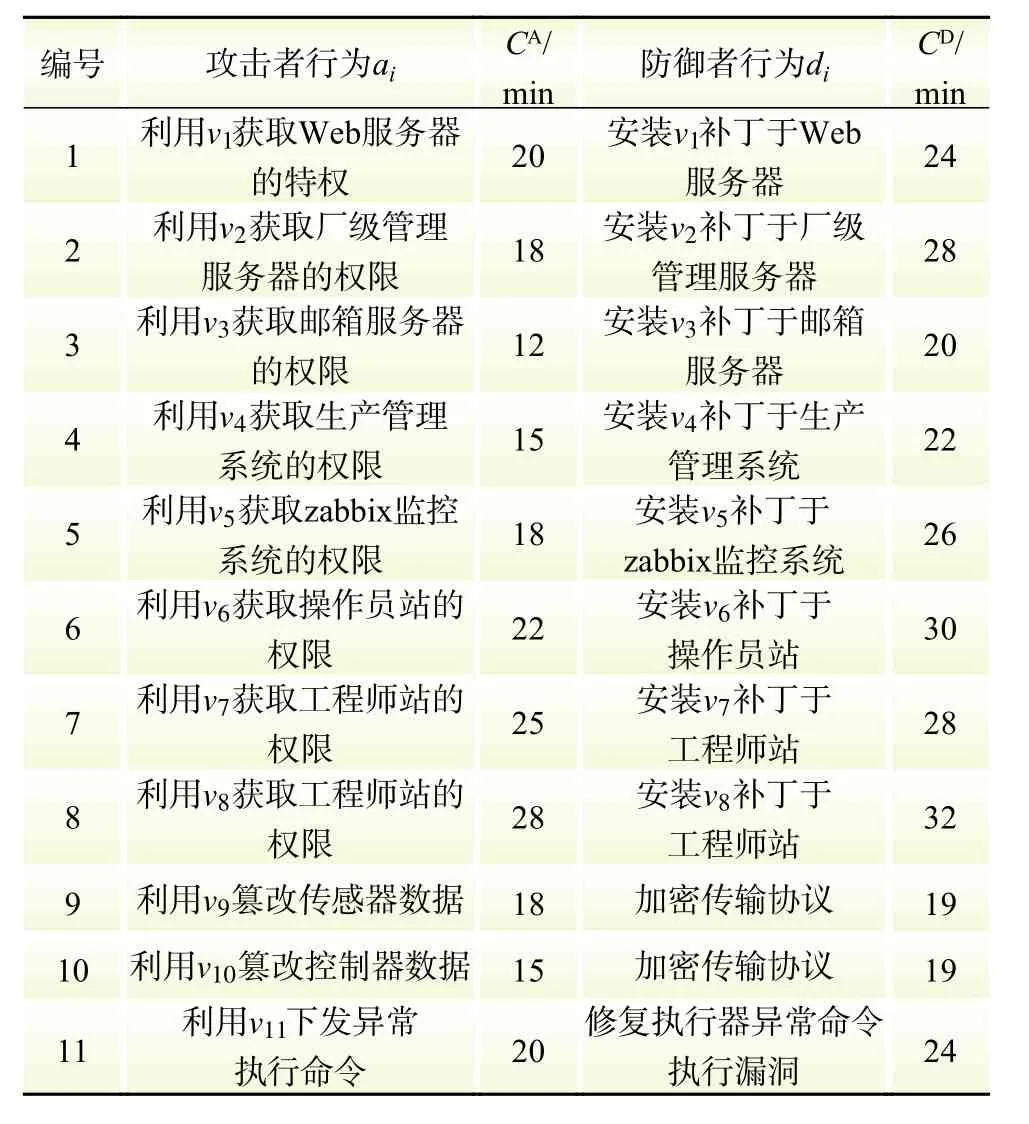
表5 攻防行为表Table 5 The actions of attackers and defenders

4.2 攻击预测结果

首先对APT攻击初始阶段攻击者信息侦查、武器构建进入到内网的行为进行预测。正收益参数 W1=10，W2=8，W3=4，W4=5。求解矩阵博弈预测攻击者行为概率分布由式（12）可求解在不同防御等级下值。

图5 攻击者动作预测Fig. 5 Prediction of attacker's actions

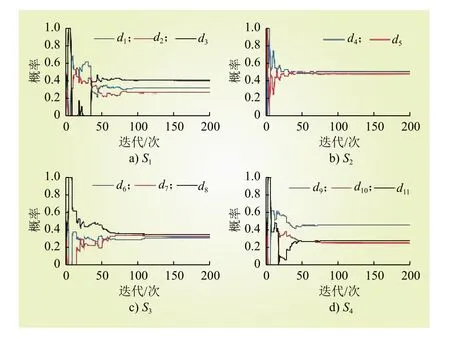
图6 最优防御行为求解Fig. 6 Solution of optimal defense actions

表6 攻防双方最优策略Table 6 Optimal strategy for attackers and defenders

4.3 入侵容忍能力评估结果

考虑CPPS试验场的防御资源有限，配备IDS系统1套、防火墙2套。防御资源可安装至外部网络至办公网络边界（）、办公网络至生产管理网络边界（）、生产管理网络至生产控制网络边界（）；生产控制网络至物理网络边界（）。将防御资源的分配方案表示为。目前试验场的分配方案为则由式(12)得根据式（2）与式（3）计算得CPPS试验场遭受网络APT攻击入侵容忍能力

考虑在有限防御资源下的最优分配方法使得CPPS的入侵容忍能力最强，分配方案结果如图7所示。实验结果表明最优资源分配方案为，此时CPPS的入侵容忍能力最强，攻击者需要消耗8 h 才能成功利用漏洞对发电物理过程进行破坏，如下发异常断电指令或篡改传感器数据等。在最优防御资源分配情况下，CPPS的可靠度曲线如图8所示。最优资源分配情况下，可靠度最高，随着时间可靠度下降幅度最小。

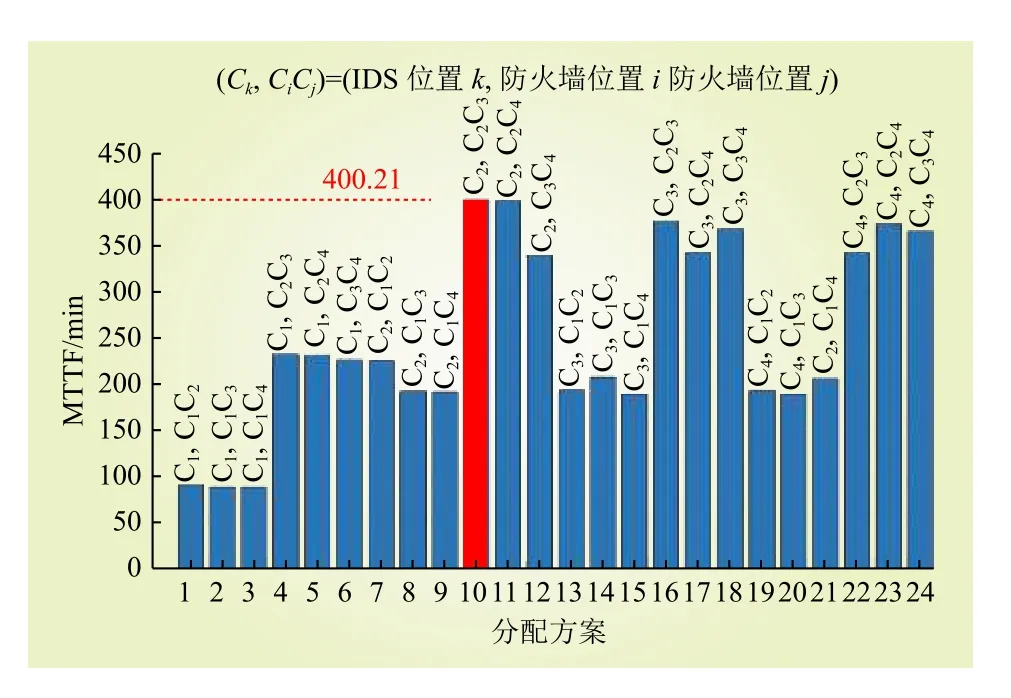
图7 防御资源分配方案结果Fig. 7 Result of the defense resource allocation scheme

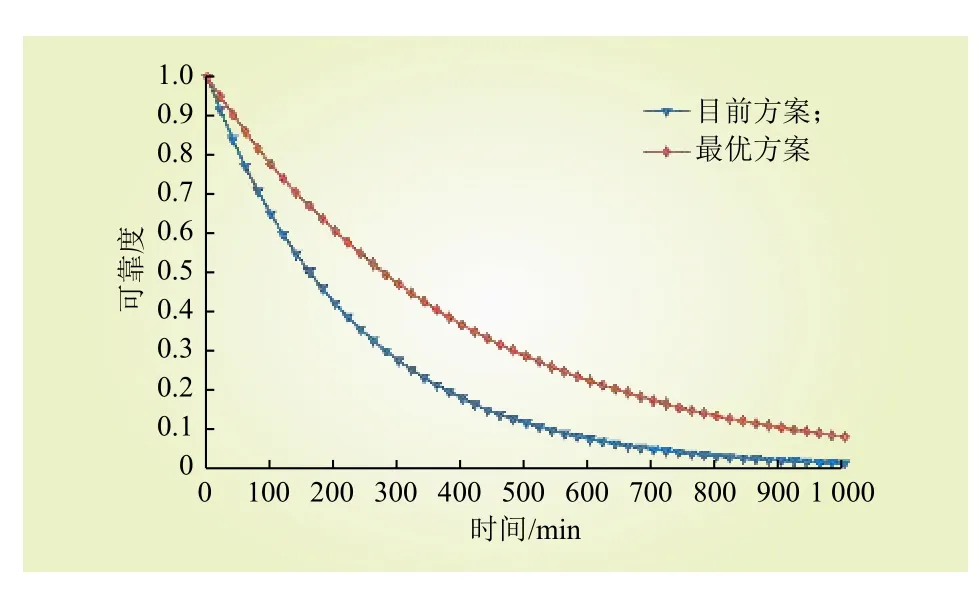
图8 最优资源分配下可靠度曲线Fig. 8 Reliability graph under optimal resource allocation

5 结语

本文提出了一种面向受攻击CPPS的入侵容忍能力评估与防御资源最优配置方法。首先，基于半马尔可夫链对APT攻击进行建模，利用随机博弈模型预测纳什均衡下攻击者的理性进攻策略，确定相应的最佳防御策略，并通过实验求解在有限防御资源条件下的最优资源分配结果，以MTTF与可靠度指标评估CPPS的入侵容忍能力。最后，以CPPS安全试验场为例验证了入侵容忍能力评估机制的有效性，为高可靠性CPPS网络的防御机制设计提供了一定借鉴。

但是，本文研究工作尚存在一些不足，提出的入侵容忍能力评估机制存在普适性不足的问题，未来工作主要研究可拓展普适通用的CPPS入侵容忍能力评估方法。