基于HYDRUS-2D 的膜调控润灌湿润锋运移数值模拟研究
2022-04-26段启蒙绳莉丽程伍群张西平韩明明吴现兵
段启蒙,绳莉丽,程伍群,张西平,韩明明,吴现兵
(河北农业大学 城乡建设学院,河北 保定 071000)
自上世纪20 年代Charle Lee 发明地下滴灌以来,经过几十年的研究与发展,地下滴灌技术已经非常成熟,但是仍然存在很多难以解决的问题。如传统地下滴灌因供水结束时管道内产生负压吸泥和作物根系的向水性造成灌水器外部堵塞[1-2]以及由重力配水导致水分下移过多[3-4]。针对地下滴灌存在的水分下移问题,国内外进行了很多研究。其中在滴灌管下铺设塑膜或箔片作为物理阻隔层,结果发现这样可以减小土壤水分的下渗,增大土壤水分的上渗高度[5-7];El-Nesr 等通过HYDRUS-2D/3D 数值模拟表明铺膜可以有效减少水下移现象[8]。王伟等在滴灌管下铺设水平或V型塑膜,在一定程度上解决了水分下移的问题[9]。程伍群等利用塑料薄膜的调节水分下移作用开发了调节水分的双膜结构,发明了膜调控润灌系统[10]。膜调控润灌系统主要依靠土壤的毛管吸力达到灌水效果,可根据土壤的含水量来对灌水量与灌水时间进行自我调节,与负压灌溉有类似的地方。负压灌溉系统也是1 种新型的将灌水器埋入地下的节水灌溉技术,主要依靠土壤的基质吸力主动吸收水分,灌水量依据土壤缺水状态而改变,能够实现自我调节[10-12]。影响传统地下滴灌土壤水运移的重要技术参数包括土壤质地结构、土壤初始含水率、滴头出流量以及埋深[13]。除了以上技术参数,膜规格是影响膜调控润灌系统土壤水分运移的关键技术参数。在1999 年国际地下水模拟中心开发的HYDRUS-2D[14]软件已经被广泛地应用于土壤水运移的模拟,并且Kandelous 和Šimůnek 通过室内和田间试验,已经证实了HYDRUS-2D 对地下滴灌土壤水运移模拟的可行性[15];Honari 等利用HYDRUS-2D/3D模型模拟了地下滴灌条件下的土壤水分运动,结果表明模拟效果良好[16]。基于以上2 个方面的考虑,笔者将选择HYDRUS-2D 软件,结合室内试验研究在通量一定的情况下不同膜规格对膜调控润灌土壤水湿润锋运移的影响,为膜调控润灌的膜规格确定和实践提供可靠的依据。
1 材料与方法
1.1 膜调控润灌灌水器
膜调控润灌技术是在传统地下滴灌的基础上改进而来的1 种新型灌溉技术,同样采用地埋式,但是膜调控润灌的灌水器与传统地下滴灌的存在着很大的差异。该技术的灌水器由4 部分组成,由上到下依次为上膜、中间透水夹层、滴头和下膜,上膜与下膜均为不透水膜,灌水器分布图1。中间透水夹层的尺寸与上膜的尺寸相同,厚度为2 mm,上膜与下膜均为正方形,下膜的尺寸大于上膜的尺寸,这样设置可以使水有更充分的时间与膜上土壤接触,由传统的重力配水为主转化为以毛管吸附配水为主。
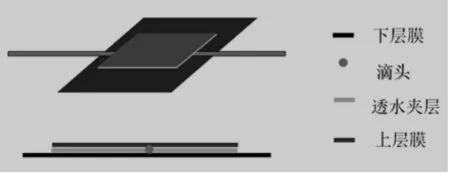
图1 灌水器分布图Fig.1 Distribution map of irrigators
1.2 膜调控润灌灌水面与通量
传统的地下滴灌都是以点源入渗的,而膜调控润灌技术则是将传统的地下滴灌由点源入渗转化为面源入渗。由图1 可知,由于中间透水夹层存在一定的厚度,实际的灌水面将是中间透水夹层前后左右4 个面。由于中间透水夹层与上膜大小是相同的,所以灌水面均处在上膜与下膜的交界处。由于本试验为面源入渗,所以灌水器的通量为滴头流量与灌水面面积的比值。
1.3 室内试验设计
采用有机玻璃试验箱进行室内试验验证数值模拟试验的可行性。室内试验采用的试验箱规格为70 cm×35 cm×70 cm( 长× 宽× 高)。试验所用土取自衡水试验田,土壤颗粒组成见下表1。

表1 土壤物理颗粒组成Table 1 Soil physical particle composition
首先将土风干过2 mm 的筛,并且采用1.4 g/cm3的容重进行分层夯实装填,每5 cm 1 层,在填装下一层时要对上一层进行打毛。供水设备采用恒位水箱,以保证滴头出流的稳定性。为了试验过程中方便观察湿润锋的形状,将灌水器的一半靠近正面观察面放置,埋深35 cm,试验装置示意图见图2。
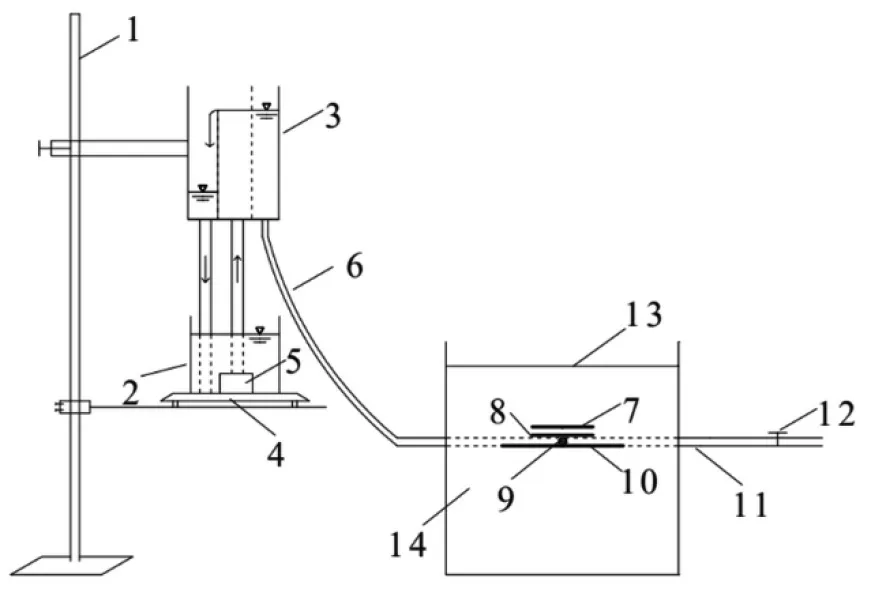
图2 试验装置示意图Fig.2 Schematic diagram of test apparatus
其观察时间采用先密后疏的原则,灌水结束后采用土钻对其膜上与膜下不同位置进行取土并用烘干法测出含水率。
1.4 模拟设计
利用数值模拟试验来研究在通量一定时膜规格的改变对膜调控润灌土壤水湿润锋运移的影响。膜处理设计4 种处理,每种处理的下膜边长均为40 cm,处理一至处理四的上膜边长分别为35、30、25 和20 cm。
1.5 模拟区域的确定
本数值模拟试验,是以下膜为基准面,下膜以上距离为正,下膜以下距离为负,灌水器埋深35 cm,膜下空间设置为35 cm。上膜与下膜均设为零通量面,灌水器中间透水夹层厚度为2 mm。膜调控润灌的土壤水运移为三维运动,由于土壤均质、各项同性,膜调控润灌土壤水分运动可作为轴对称二维问题处理[17],以处理二为例,其研究区域如图3 所示(以滴头位置为原点,可表示区域内具体位置,为了方便观察横坐标移至区域顶端,下同),为了更好地研究膜上与膜下水量的分布,以下层膜为分界面,将研究区域划分为2 个计算区域,下层膜以上为1 个计算区域,下层膜以下为另外1 个计算区域。
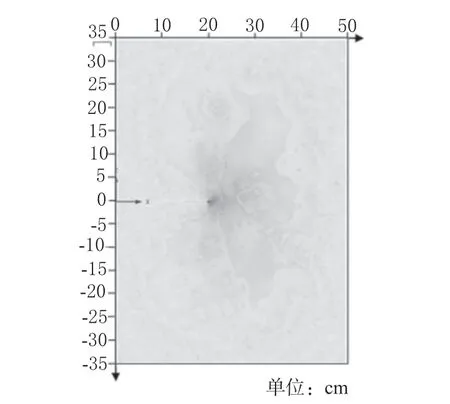
图3 研究区域Fig.3 Study area
1.6 控制方程
根据达西定律与质量守恒定律,在不考虑根系吸水的情况下,土壤水模拟的控制方程采用二维Richard 方程如式(1):
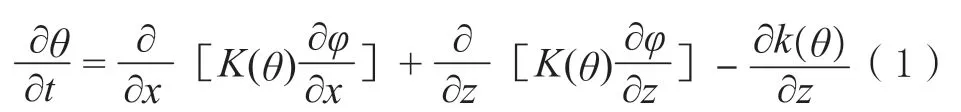
式中:θ—土壤体积含水率,cm3/cm3;
t—入渗时间,min;
K(θ)—土壤非饱和导水率,mm/min;
φ—土壤总水势,cm,对于非饱和土,φ=φm±z中φm为土壤基质势;
z—垂直坐标,原点坐标以上为正,以下为负。
对于HYDRUS-2D 软件,其中能够模拟土壤水分入渗的过程的模型有5 种,本研究在没有作物的情况下要选用van Genuchten 模型,对土壤水运移规律进行描述,van Genuchten 模型[18]如式:
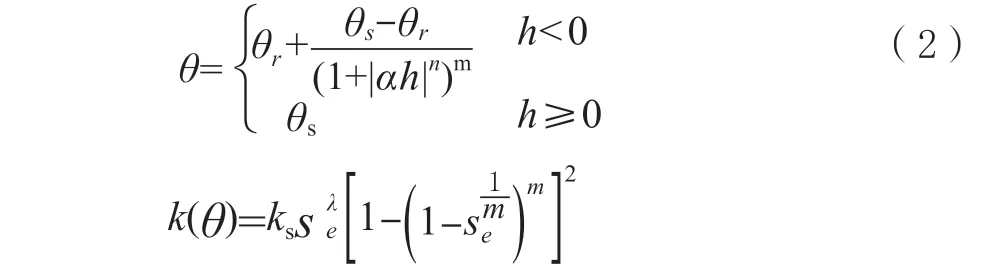
式中:θr—土壤剩余含水率,cm3/cm3;
θs—土壤饱和含水率,cm3/cm3;
ks—饱和导水率,cm/min;
se—土壤有效含水率,cm3/cm3;
h—土壤吸力,cm;
α、λ、m、n为经验参数,se=(θ-θr)/(θs-θr);m=1-1/n,n>1。
1.7 定解条件
如下图4 所示。
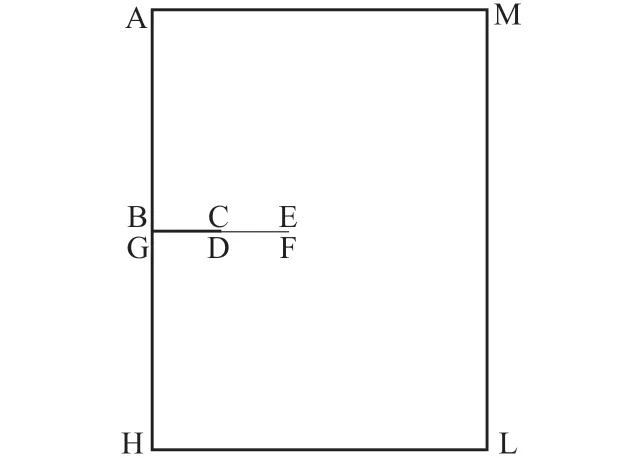
图4 计算区域Fig.4 Computational domain
计算区域各个节点的坐标点A(0,350),B(0,2.1),C(x0,2.1),D(x0,0.1),E(200,0.1),F(200,0),G(0,0),H(0,-350),L(500,-350),M(500,350)。(单位:mm)
说明:如下图5 为放大的B、C、D、E、F、G的位置图。

图5 细节放大图Fig.5 Detail enlarged
EF 表示为下层膜,2 点之间的距离也就是下膜的厚度为0.1 mm;对于x0,表示为上层膜边长的1/2;CD 表示为透水夹层的厚度,为2 mm,所以C点横坐标为上层膜边长的1/2,纵坐标为下层膜厚度与透水夹层厚度之和,即(x0,2.1)。
(1)初始条件,表示为:
θ(x,z,t)=θ0(x,z,0) (0 ≤x≤5 0 0,350 ≤z≤350)
式中θ0(x,z,0)为土壤初始含水率,cm3/cm3;
(2)边界条件
AB、GH、EF、ML 零 通 量 边 界-K(θ)=0,t≥0 (0 ≤x≤500, -350 ≤z≤350)
CD恒定流量边界q=-K(θ)=q0(x,z,t),t≥0(x=x0,0.1 ≤z≤2.1)
式中:q0恒定流量,x0上膜边长的1/2。
2 结果与分析
2.1 参数率定
对于4 种膜处理所采用的土壤与其室内试验保持一致,依据所用土壤的物理颗粒组成的配比以及土壤容重,利用HYDRUS-2D 中自带神经网络对土壤水力参数进行了初步预测,其预测后的土壤水力参数如下表2。然后选择处理三的试验结果对模型中土壤水力参数进行了率定,经率定后的土壤水力参数见表3。

表2 预测后土壤水力参数表Table 2 Table of soil hydraulic parameters after prediction

表3 率定后土壤水力参数表Table 3 Soil hydraulic parameters after calibration
图6 为数值模拟所插观测点。

图6 观测点分布Fig.6 Observation point distribution
表4 为经参数率定后模型所模拟的各个观测点灌水339 min 后停止灌水时实测值与模拟值的相对误差。可以看出各点含水率的实测值与模拟值的相对误差大部分都在10%以内,表明了率定后所得的土壤水力参数具有一定的准确性。
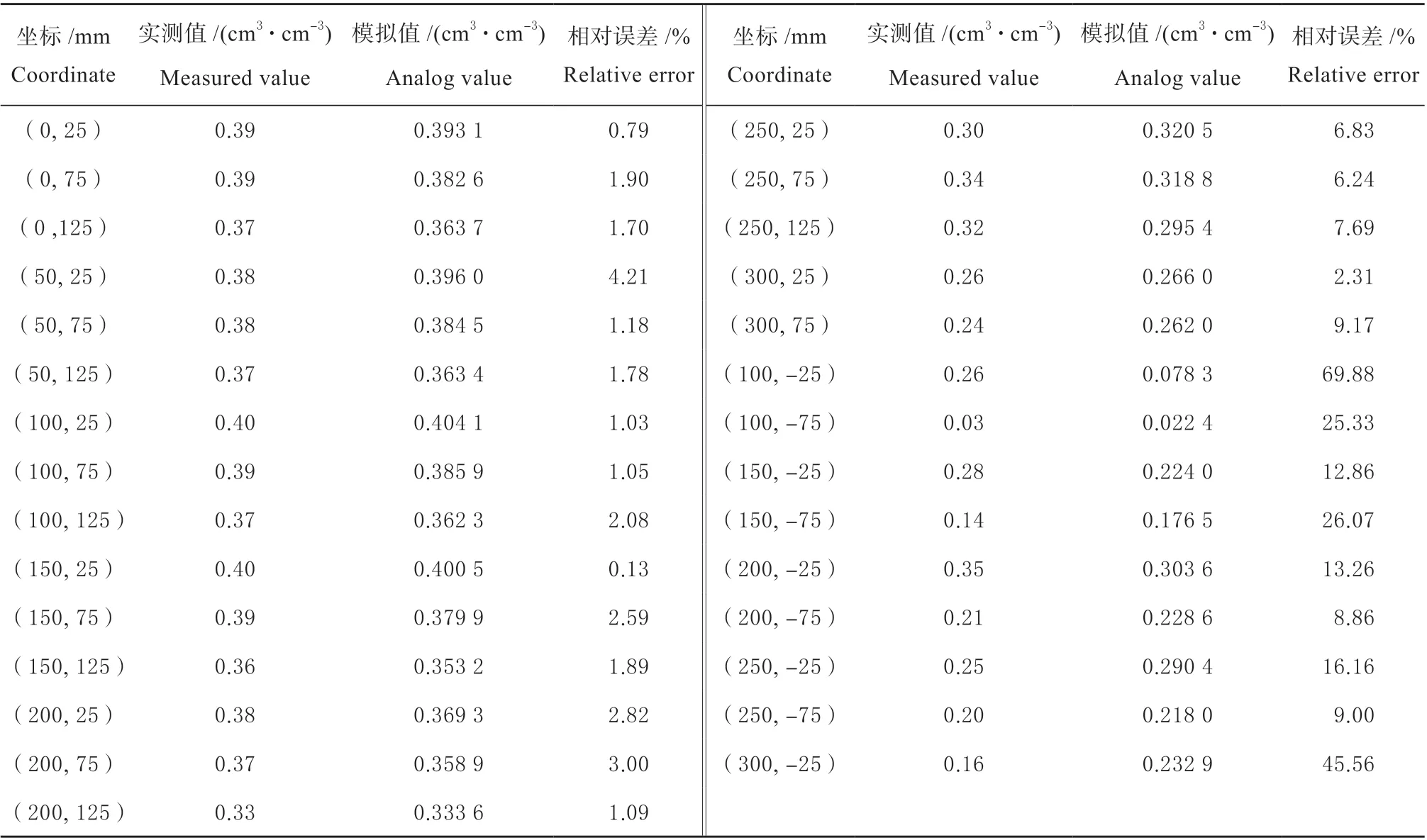
表4 土壤含水率实测值与模拟值的相对误差Table 4 The relative error of soil moisture content between the measured value and the simulated value
图7 ~9 给出了用率定好的土壤水力参数试验湿润锋各向的实测值以及数值模拟湿润锋模拟值的对比图。
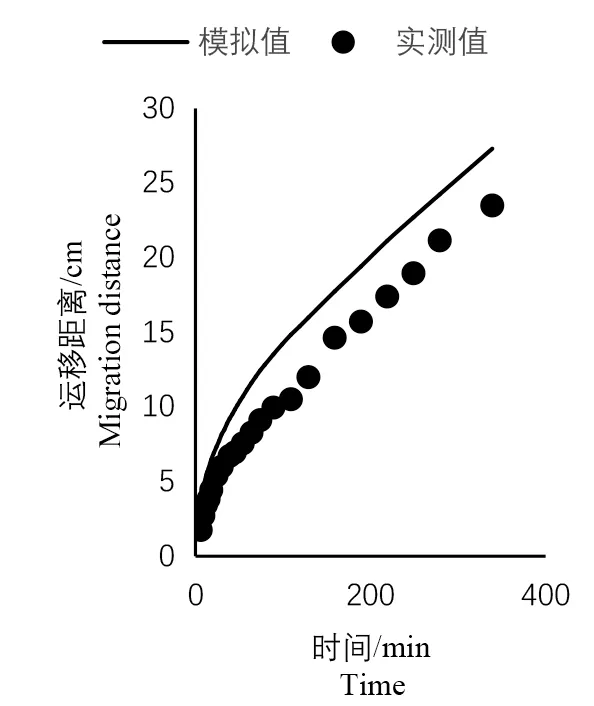
图7 垂直向上对比图Fig.7 Vertical upward comparison chart
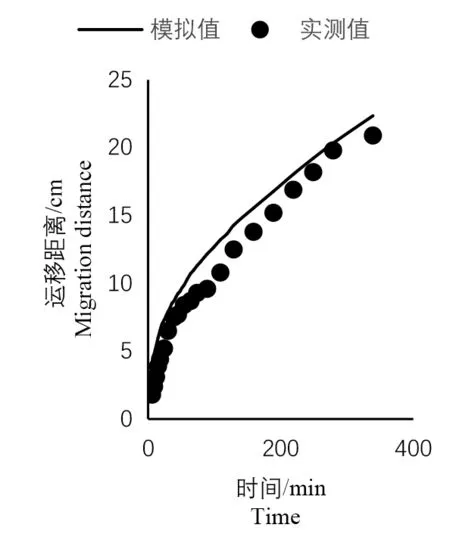
图8 水平向右对比图Fig.8 Horizontal right comparison chart
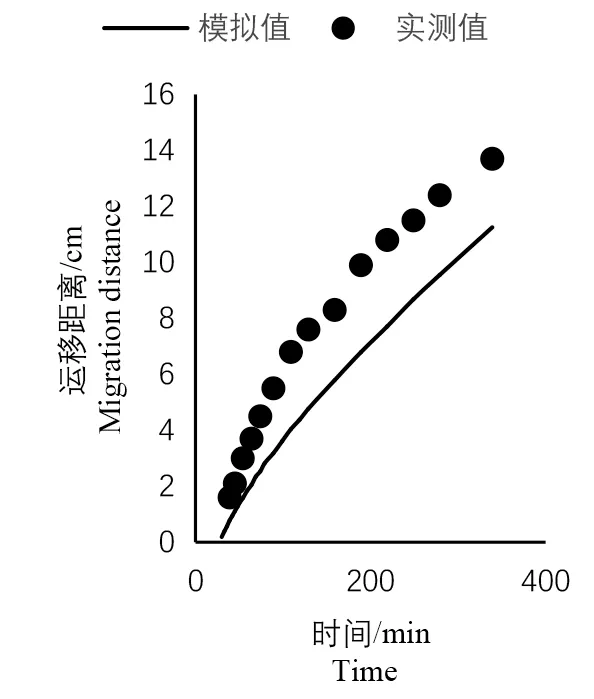
图9 垂直向下对比图Fig.9 Contrast the graph vertically downward
由于试验存在一定的膜间渗漏,所以模拟值与实测值存在一定的差异性。湿润锋运移距离垂直向上、水平向右和垂直向下的模拟值与实测值的均方根误差分别为3.07、1.83、2.37 cm,均方根误差变化范围为1.83 ~3.07 cm,3 个方向全部湿润锋运移距离的模拟值与实测值的均方根误差为2.49 cm。
2.2 模型验证
室内试验选用膜处理二对率定完成后土壤水力参数如表2 的准确性进行验证,表5 为各个观测点灌水339 min 后停止灌水时实测值与模拟值的相对误差。
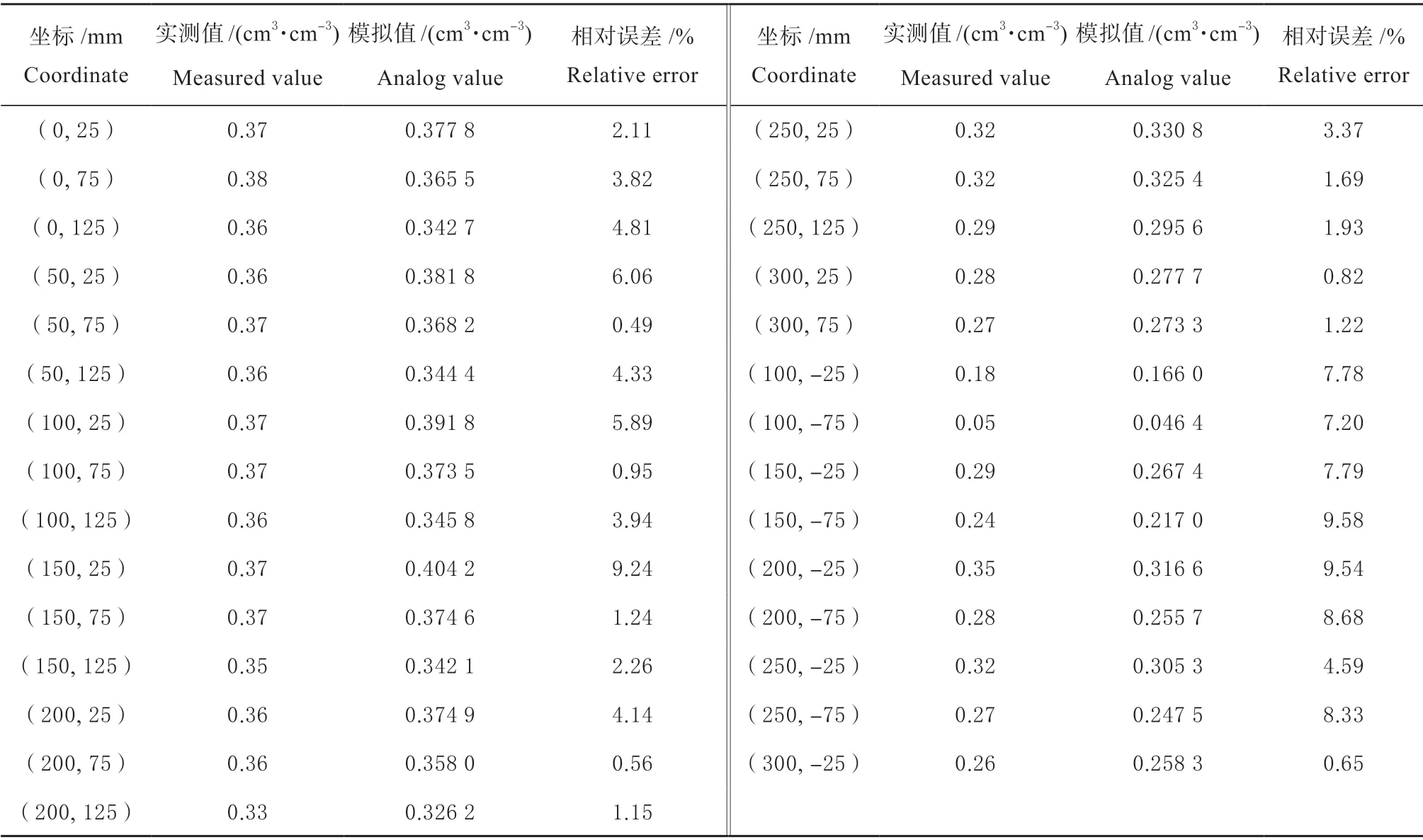
表5 土壤含水率实测值与模拟值的相对误差Table 5 The relative error of soil moisture content between the measured value and the simulated value
可以看出各点含水率的实测值与模拟值的相对误差都在10%以内,并且相对误差的平均值为4.28%,在5%以内,两者具有很好的一致性[19,20],说明膜调控润灌应用数值模拟试验来模拟的可行性,具有一定的准确性。
图10 ~12 给出了试验湿润锋各向的实测值以及数值模拟湿润锋模拟值的对比图。由于试验存在一定的膜间渗漏,所以模拟值与实测值存在一定的差异性。湿润锋运移距离垂直向上、水平向右和垂直向下的模拟值与实测值的均方根误差分别为3.20、2.08、1.28 cm,均方根误差变化范围为1.28 ~3.20 cm,3 个方向全部湿润锋运移距离的模拟值与实测值的均方根误差为2.41 cm,表明模拟值与实测值存在很好的一致性[21]。图10 ~12 进一步说明了数值模拟地下膜调控润灌的可行性以及模拟的精度较好。
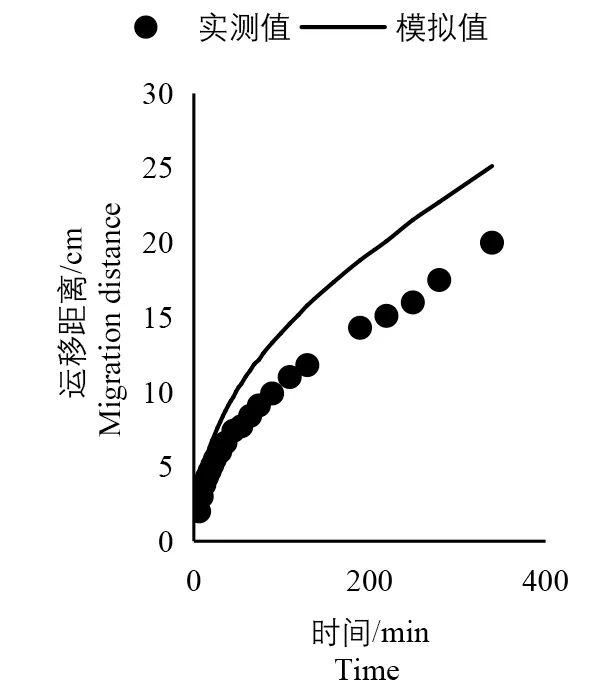
图10 垂直向上对比图Fig.10 Vertical upward comparison chart
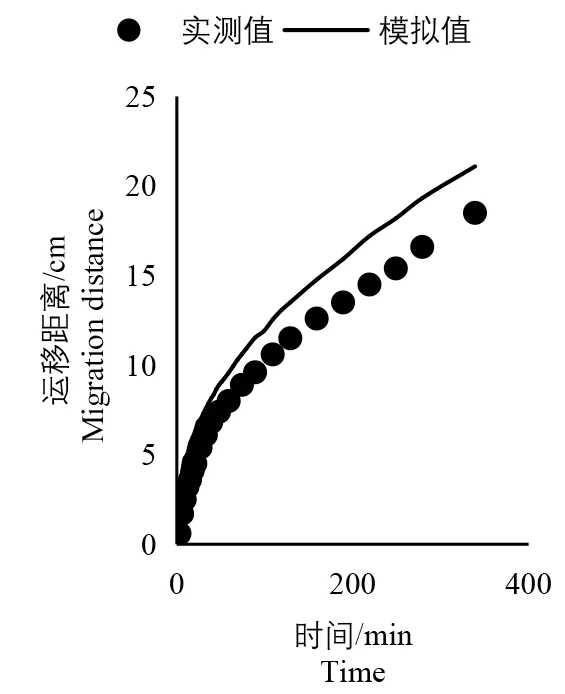
图11 水平向右对比图Fig.11 Horizontal right comparison chart
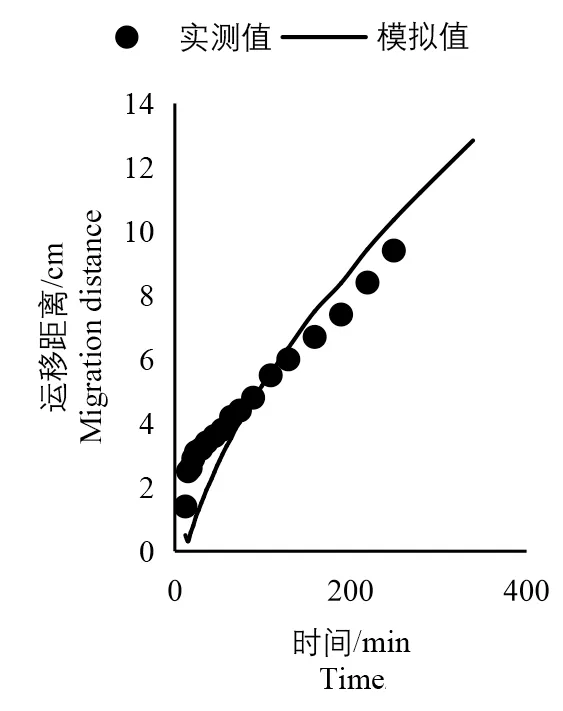
图12 垂直向下对比图Fig.12 Contrast the graph vertically downward
2.3 湿润锋运移阶段的划分
湿润锋的运移规律是研究土壤水运移的重要部分。当通量保持不变的情况下,膜大小的改变会影响土壤水的运移。通过数值模拟试验可将膜调控润灌的入渗过程分为3 个阶段:
第1 阶段(膜上运移阶段):灌水面出水短膜出现湿润锋——湿润锋运移到下膜的边界,如图13所示;

图13 膜上运移阶段Fig.13 Upper membrane migration stage
第2 阶段(膜下运移阶段):湿润锋运移到下膜边界开始存在膜下入渗——膜上湿润锋左右开始融合,如图14 所示;

图14 膜下运移阶段Fig.14 Inferior membrane migration stage
第3 阶段(左右交融运移阶段):膜上湿润锋左右开始融合——入渗结束,如图15 所示;
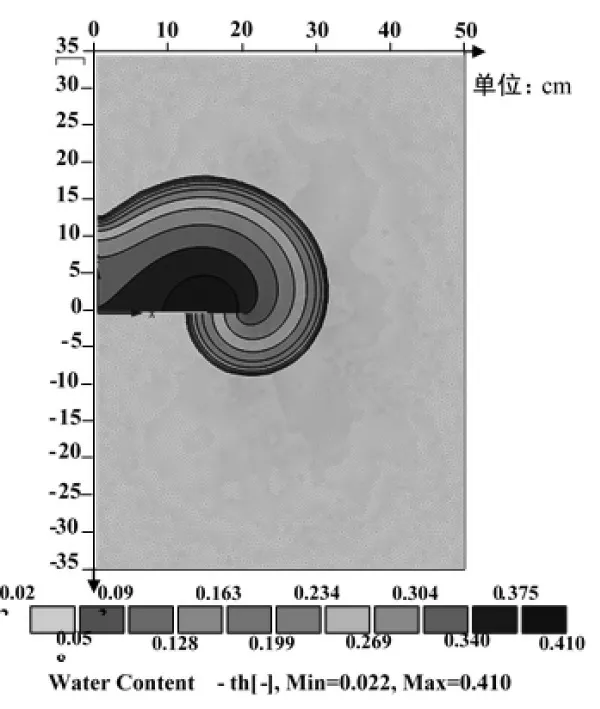
图15 左右交融运移阶段Fig.15 Left and right blending migration stage
2.4 膜调控润灌湿润锋的形状
对于传统的地下滴灌湿润体形状的研究,通过试验已经发现湿润体剖面一般为半椭圆形,湿润体为半椭球体[22]。对于膜调控润灌,在灌水初期,由于膜的阻挡作用,湿润锋只会垂直向上和水平方向运移,其湿润体截面形状为以上膜边界为圆心的上半圆,如上图13 所示;随着湿润锋向四周继续运移,湿润锋超出下膜,水将开始下渗,下渗部分的截面形状是以下膜边界为圆心的不规则下半圆,如图14 所示;在入渗的后期,膜上两端湿润锋开始交汇继续向上运移;当入渗结束时,其湿润体截面将呈现出耳蜗形状如图15 所示。
2.5 膜规格对水量分布的影响
以下膜所处的面为基准面,其4 个处理的膜上与膜下的水量百分比对比图如图16 所示,可以看出膜规格的改变对于膜上与膜下(膜指的是双模结构中的下层膜)水量有明显的调控作用。当上膜最小时,膜上的水量百分比最大,占总水量的79.57%,膜的调控作用最明显;上膜最大时,膜上的水量百分比就会是最小的,占总水量的66.33%,膜的调控作用比较差,处理四比处理一上膜的水量多13.24%。由此可知当上膜尺寸递减时,膜调控作用的明显性呈增大趋势,膜上所保留的水量将会呈增多趋势,下膜的水量百分比则相反。
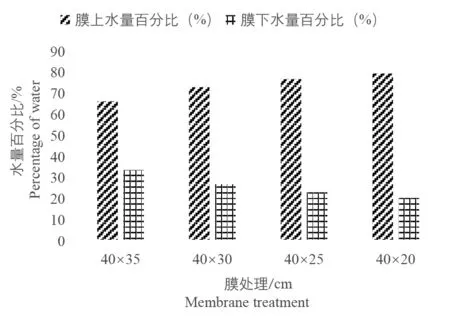
图16 膜上与膜下水量百分比对比图Fig.16 Comparison of the percentage of water on and under the membrane
2.6 膜规格对湿润锋运移规律的影响
当通量一定时,膜的4 个处理在入渗时湿润锋的运移是有差异的。4 个膜规格处理最后结束时的结果如图17:

图17 湿润锋模拟结果图Fig.17 Simulation results of wetting front
在同一方向上,不同膜处理时湿润锋运移距离与入渗时间的关系见图18 ~20。
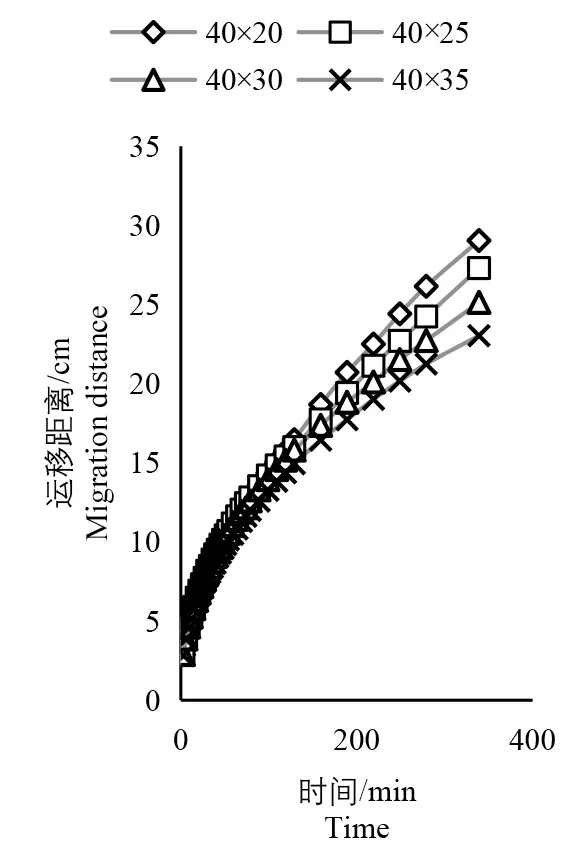
图18 湿润锋垂直向上运移对比图Fig.18 Comparison of the vertical upward migration of the wet front
图18 ~20 为通量一定时不同膜处理的不同方向湿润锋运移与时间的关系图。从对比图可以发现湿润锋在不同方向上的运移速率随着入渗时间的增大运移速率呈减小趋势。入渗初期,湿润锋的运移会非常快,灌水面周围的土壤含水量较低,灌水面周围会形成较高的土水势;随着灌水时间的延长,湿润体的体积增加,湿润体内部的含水量也会增加,灌水面周围所造成的饱和区域也会增大,微润带的入渗流量会随着饱和区域的增大而减小,湿润锋的运移速率也会变慢。经过试验可知,对于传统的地下滴灌随着入渗时间的延长,其湿润锋运移的速率将会呈减小趋势[23-24]。膜调控润灌的湿润锋运移速率的变化与传统地下滴灌保持一致。
图18 为4 种膜处理湿润锋垂直向上运移距离与时间关系图,可以看出在入渗前期4 种膜处理湿润锋垂直向上的运移距离差距不是很大,这是由于前期4种膜处理大部分仍处在膜上运动阶段,运动状态相同;在入渗后期,4 种膜处理湿润锋垂直向上的运移距离差距呈增大趋势,膜处理四的垂直向上运移距离最大,为29.04 cm,膜处理一的垂直向上运移距离最小,为23.03 cm;图19 为4 种膜处理湿润锋垂直向下运移距离与时间的关系图,可以看出膜处理四的垂直向下运移距离反而最小,为10.06 cm,膜处理一的垂直向下运移距离反而最大,为15.13 cm。分析图18 与图19,各个膜处理湿润锋垂直向上的运移距离都要大于垂直向下的湿润锋,并且上膜在变小的同时湿润锋垂直向上的运移距离在增大,湿润锋垂直向下的运移距离在减小,就会出现湿润锋垂直向上运移距离最大的膜处理相对应的湿润锋垂直向下的运移距离会最小。
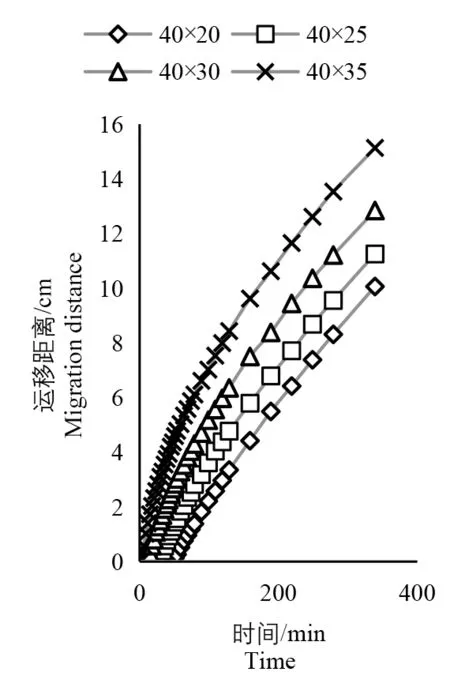
图19 湿润锋垂直向下运移对比图Fig.19 Comparison of the vertical downward migration of the wet front
图20 为水平向右不同膜处理湿润锋运移与时间的关系图,可以看出随着上膜的变小,湿润锋水平向右的运移距离也随之减小,膜处理四的水平向右运移距离最小,为34.28 cm;膜处理一的水平向右运移距离最大,为38.18 cm。在入渗的前期4 种膜处理的水平向右运移的差距还是比较大,但随着入渗时间的增加4 种膜处理的水平向右运移的差距呈减小趋势。入渗后期上膜大的处理重力对土壤水的影响要大于前期,相比较上膜小的会有更多的土壤水膜下渗漏,造成了随着入渗时间的增加4 种膜处理的水平向右运移的差距呈减小趋势。
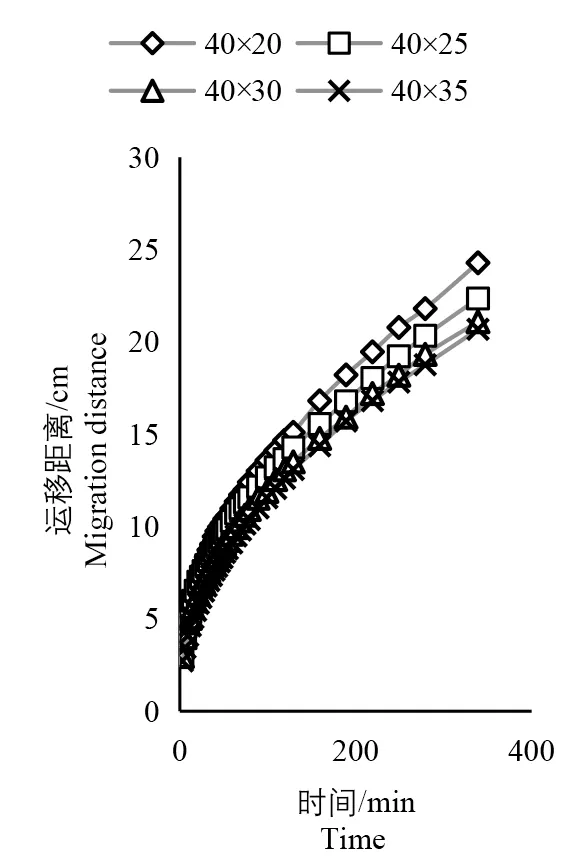
图20 湿润锋水平向右运移对比图Fig.20 Comparison of the horizontal migration of the wet front to the right
2.7 湿润锋运移距离与时间的关系
根据散点图进行函数拟合湿润锋各向运移距离与时间的关系,如表6 所示。
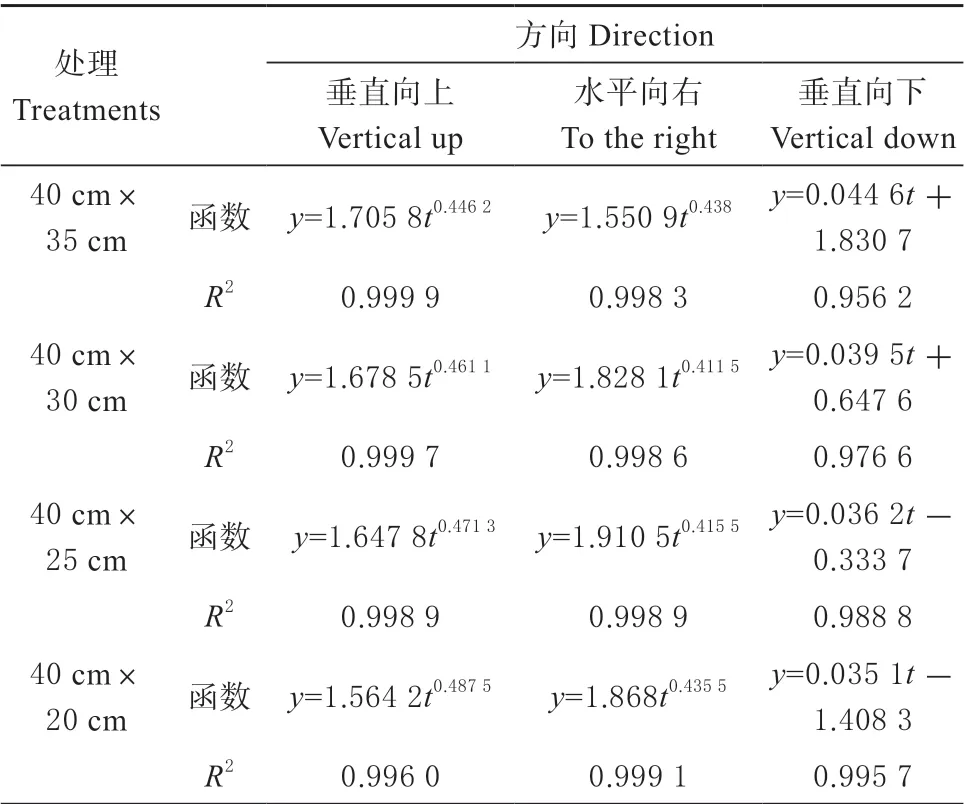
表6 湿润锋运移距离与时间的函数关系Table 6 The migration distance of wet front is a function of time
拟合结果表明,垂直向上与水平向右的湿润锋运移距离与时间的变化关系,能够拟合成函数y=mtn,并且决定系数R2在0.99 以上,非常接近1,达到显著水平,说明4 个处理的膜调控润灌入渗过程中,湿润锋垂直向上与水平向右运移距离与时间存在幂函数关系;垂直向下的湿润锋运移距离与时间的变化关系,能够拟合成函数y=kt,决定系数R2在0.95 以上,非常接近1,也达到了显著水平,说明4 个处理的膜调控润灌入渗过程中,湿润锋垂直向下运移距离与时间存在线性关系。对于传统地下滴灌,其湿润锋各个方向运移距离与时间的关系已经通过试验得出存在很好的幂函数关系[25-27]。由此可以看出,膜调控润灌湿润锋垂直向上与水平向右运移距离与时间的关系与传统地下滴灌保持一致,垂直向下的与传统的地下滴灌存在着较大的差异。垂直向上的湿润锋运移距离与时间的函数关系拟合中随着上膜的变小决定系数R2也在变小,显著水平在降低;水平向右与垂直向下的与之相反,随着上膜的变小显著水平呈增大趋势,见表6。
3 讨论
膜调控润灌是基于地下滴灌而来的1 种全新灌溉方式,膜调控润灌土壤水运移规律与传统地下滴灌的土壤水运移规律既有保持一致的地方又有不同的地方。对于传统地下滴灌的数值模拟,Kandelous和Šimůnek 通过室内和田间试验,已经证实了HYDRUS-2D 对地下滴灌土壤水运移模拟的可行性[15];Honari 等利用HYDRUS-2D/3D 模型模拟了地下滴灌条件下的土壤水分运动,结果表明模拟效果良好[16]。基于HYDRUS-2D 探究在通量一定时膜规格对膜调控润灌湿润锋运移的影响,第一步要验证HYDRUS-2D 对膜调控润灌数值模拟的准确性。通过对膜规格40 cm×30 cm 各个观测点土壤含水率实测值与数值模拟值进行对比,相对误差均小于10%,平均值在5%以内,湿润锋运移距离的模拟值与实测值的均方根误差也保证了在合理的范围之内,充分说明了HYDRUS-2D 对膜调控润灌数值模拟的准确性。
通过对膜调控润灌土壤水分运移的模拟,可以很清晰地看出运移过程可以分为3 个阶段,第1 个阶段为膜上运移阶段,第2 个阶段为膜下运移阶段,第3 个阶段为左右交融运移阶段,这与传统地下滴灌存在着很大的差异。土壤水分在运移的过程中,随着入渗时间的增加,运移速率在不断地减小。对于传统的地下滴灌经过试验可知,随着入渗时间的延长,其湿润锋运移的速率将会呈减小趋势[21-22]。膜调控润灌的湿润锋运移速率的变化与传统地下滴灌保持一致。对于4 种膜处理,在通量一定的情况下,土壤水分运移前期湿润锋的运移会非常快,随着灌水时间的增加,湿润体体积的增加,伴随着饱和区域的增大湿润锋的运移速率会变慢,并且各个膜处理湿润锋垂直向上的运移距离都要大于垂直向下的运移距离。对于计算区域划分膜上与膜下2 个区域,灌水结束后各个膜处理的膜上水量都要大于膜下的水量,并且伴随着上膜不断减小膜上水量在不断增加。上膜变小湿润锋垂直向上运移距离增大以及上膜变小膜上水量也在不断增加的原因是上膜变小可使得更多的水量保持在膜上位置,使得膜上的土壤有更充分的时间利用毛管吸力对水分进行吸收,与此同时由于下膜的阻挡作用削减了重力对土壤水的影响,这样减少了土壤水的膜下渗漏。传统的地下滴灌土壤水分运移由于重力配水会导致土壤水分下移过多[3-4],经过研究膜调控润灌与地下滴灌相比能够很好地解决地下滴灌深层渗漏的问题。图17 可以清晰地看到当通量一定时随着上膜的不断增大湿润锋所能到达的右边界越远,但是相对应的土壤水分垂直向上的运移距离会变小。当土壤水分垂直向上运移距离最大时,膜下渗漏的水量最小,湿润锋到达右边界的距离也是最小的,却不利于相邻2 个灌水器湿润锋的搭接。
对于湿润锋各向运移距离与时间的关系,根据散点图进行了函数拟合。对于膜调控润灌,垂直向上与水平向右的湿润锋运移距离与时间存在幂函数关系,对于传统地下滴灌,其湿润锋各个方向运移距离与时间的关系已经通过试验得出存在很好的幂函数关系,2 种灌溉方式存在一致性[25-27]。对于膜调控润灌,湿润锋垂直向下的运移距离与时间的函数关系拟合存在很好的线性关系,与传统地下滴灌存在很大的差异性。
4 结论
通过以上内容的研究表明,利用HYDRUS-2D软件所建立的土壤入渗模型能够很好地模拟出膜调控润灌土壤水分运移的规律,可以用来研究膜规格的变化对膜调控润灌湿润锋运移的影响。在膜规格的改变情况下能够调控膜上下湿润锋的运移距离和水量百分比。在试验通量和土质一致条件下,随着上膜尺寸的减小,其入渗结束时湿润锋向上运移的距离呈增大趋势,而在水平方向与竖直向下的运移距离呈减小趋势,有效地减少了膜下渗漏的水量。在研究膜调控润灌湿润锋运移距离与时间的关系中,垂直向上与水平方向湿润锋运移距离与时间存在着显著的幂函数关系;垂直向下湿润锋运移距离与时间存在着显著的线性关系。
