三相精密程控标准源的设计与实现

王伟红，金 立，叶丽雅，王培宏，李少白

（1.国网浙江省电力有限公司培训中心，杭州 310015；2.国网浙江杭州市余杭区供电有限公司，杭州 311100）

0 引言

三相精密程控标准源是为电能监测仪表校准而研制的一种以定点或步进方式输出标准电压、电流与功率的装置，可产生幅度、相位、频率可调的高精度多量程三相工频（谐波）电压、电流信号，作为各类电能表、电能质量监测仪器校对与检定的基准信号，广泛应用于计量、测量等领域［1-2］。

目前我国正在积极推进OIML（国际法制计量组织）颁布的OIML R46电能表国际建议。根据对OIML R46国际建议的解读，传统程控标准源在小电流输出、谐波试验等方面存在个别项目无法开展的困难［3］。在小电流输出方面，OIML R46国际建议明确要求对0.2S 级的3×0.3（1.2）A 电能表在3 mA 时的电能准确度进行检定［4］。在谐波试验方面，IR46 标准增加了方波影响试验、尖顶波影响试验和高次谐波影响试验，所规定的测试波形能更加全面地模拟电能表现场运行工况［5］。因此，需要研制出一款较传统程控标准源具有更高精度、更好稳定性以及更快响应速度的程控标准源。

标准源需要为检测对象提供电源，因此标准源电压输出端针对非线性瞬变负载的带载能力是衡量标准源的重要指标之一。文献［6］采用脉冲宽度调制技术以提高标准源的带载能力。文献［7］采用功率运算放大器实现程控功率源，基于瞬时分量法的快速反馈控制算法提升功率输出的稳定性。然而控制策略多采用比例控制或比例积分控制，比例控制无法实现零静差控制，比例积分控制则缺乏对各次谐波的抑制［8］，尤其是缺乏对小电流输出的针对性处理与反馈信号测量的频谱泄露与栅栏效应抑制处理。因而在非线性瞬变负载较大时，标准源的静态输出精度与动态响应能力均存在不足。

本标准源一方面通过优化DDS（直接数字波形合成器）架构、高精度D/A（数模）转换、小电流分段等方式提升参考波形精度，采用加窗FFT（快速傅里叶变换）插值运算提升反馈信号的测量精度；另一方面采用以动态环为内环、稳态环为外环的双环控制策略，兼顾标准源的响应速度、输出稳定性与精度。以滞环控制为核心的动态环可极大提升标准源的动态响应能力，从而增强高次谐波的输出能力以及非线性负载的带载能力。以比例积分控制为基础的稳态环保证了标准源的输出稳定性。基于Rife-Vincent（I）窗的FFT 插值运算能有效抑制频谱泄露和栅栏效应，其反馈信号测量精度的增强也确保了标准源的稳态输出精度。

1 总体框架

三相精密程控标准源采用DDS 构成数字信号源，通过高精度D/A 转换器转换为模拟信号。模拟信号经数字功放扩容后，通过滤波、升压、升流等环节为用户提供标准电压、电流。其总体框架原理如图1所示。

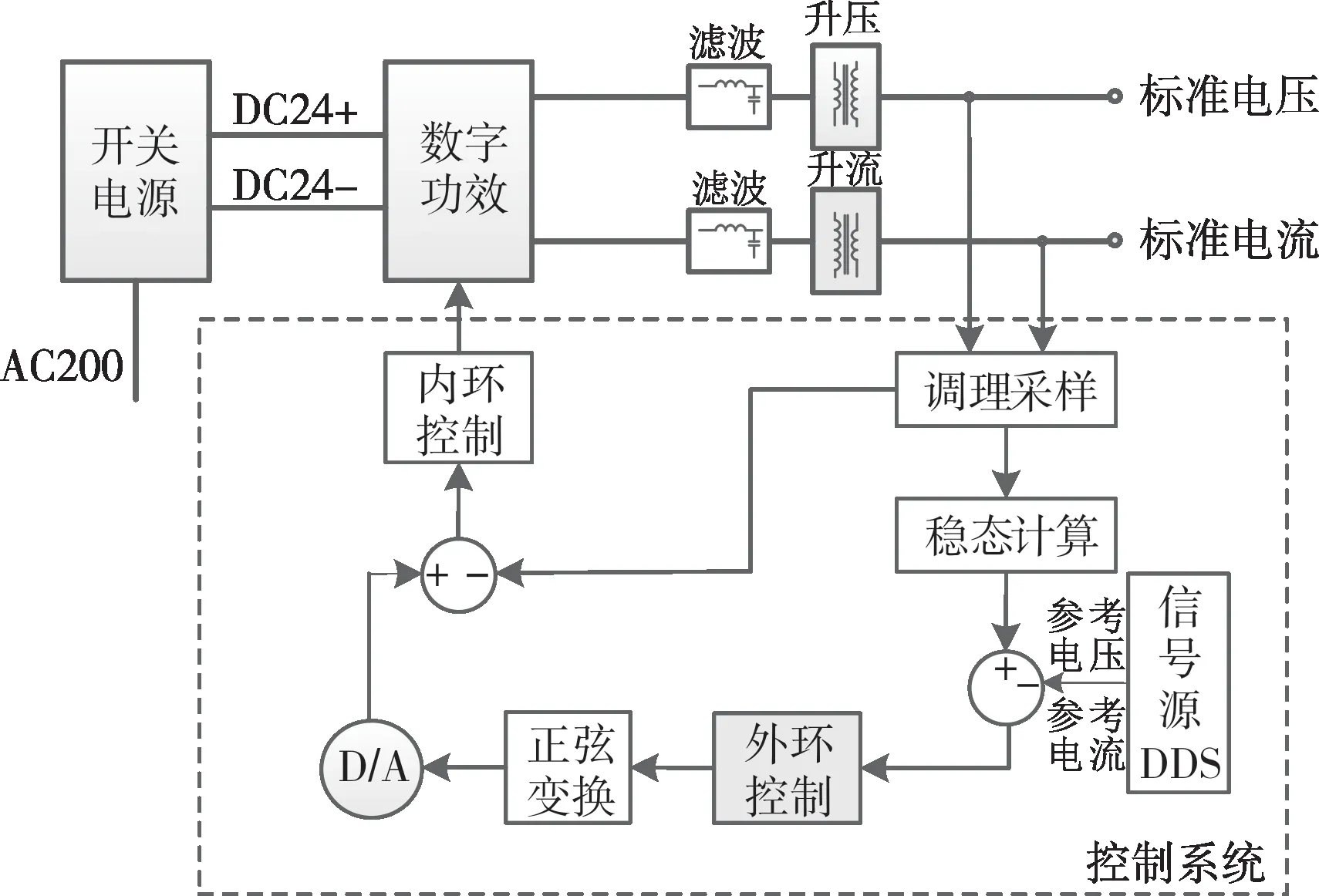
图1 三相精密程控标准源原理框图

1.1 DDS的结构优化

DDS 是一种从相位角度出发的全数字化波形合成技术和信号发生方法，具有分辨率高、频率切换时间快、可编程控制等突出优点，而且能够在频率改变时保持相位的连续。因此，DDS 在通信、测试、仪器仪表领域得到了广泛应用［9］。

DDS 的基本原理如图2 所示，它主要由基准时钟fb、频率控制字、相位累加器、波形存储器组成。图2中：L为相位累加器的位数；M为波形存储器地址的位数；D为波形值位数，即D/A 转换器的位数。

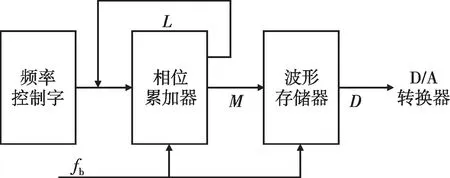
图2 DDS基本原理框图

DDS 开始工作后，基准时钟fb的每个脉冲将引发相位累加器的输出增加单步长的相位，该单步长的相位增量由频率控制字决定。以相位累加器的输出为波形存储器的地址，DDS 从波形存储器中获取数字化的波形值。D/A 转换器将该数字量转成模拟阶梯信号，并通过下一级的低通滤波器进一步滤除杂散信号，从而平滑阶梯信号，得到所需的模拟波形。

为提高DDS 输出信号的相位精度，一般来说DDS 相位累加器的位数L比波形存储器的地址位数M大。因此只能使用相位累加器的高M位作为波形存储器的寻址位数，这样必然会产生相位截断误差。

针对上述问题，在传统DDS 结构的基础上改进相位累加器，优化波形存储器的数据提取过程，并增加一个插值修正环节对波形存储器输出的信号值进行修正，以期提高DDS输出波形的精度。

1）相位累加器的改进：当相位累加器达到设定的溢出值后，以余值而不是0作为下一次累加的起始值。

2）波形存储器数据提取的优化：插值修正环节利用相位累加器的高M位作为寻址地址，获得该地址位以及前后两个相邻地址位的波形值，并结合被截（L-M）位的相位进行三阶拉格朗日插值，从而弱化截断误差造成的精度影响。

1.2 高精度D/A转换电路

由于市场上24位D/A转换芯片较少，且不易采购，故采用了一款两通道16位电流型D/A转换芯片LTC2752，结合精密运算放大器LT1469 实现24位分辨率的D/A转换模拟信号输出，原理框图如图3所示。其中：Rf和If分别为LTC2752芯片内的参考电阻和电流；Ia和Ib为两通道D/A转换输出电流；Ra和Rb为两通道D/A 转换的取样电阻；Uout为输出信号。

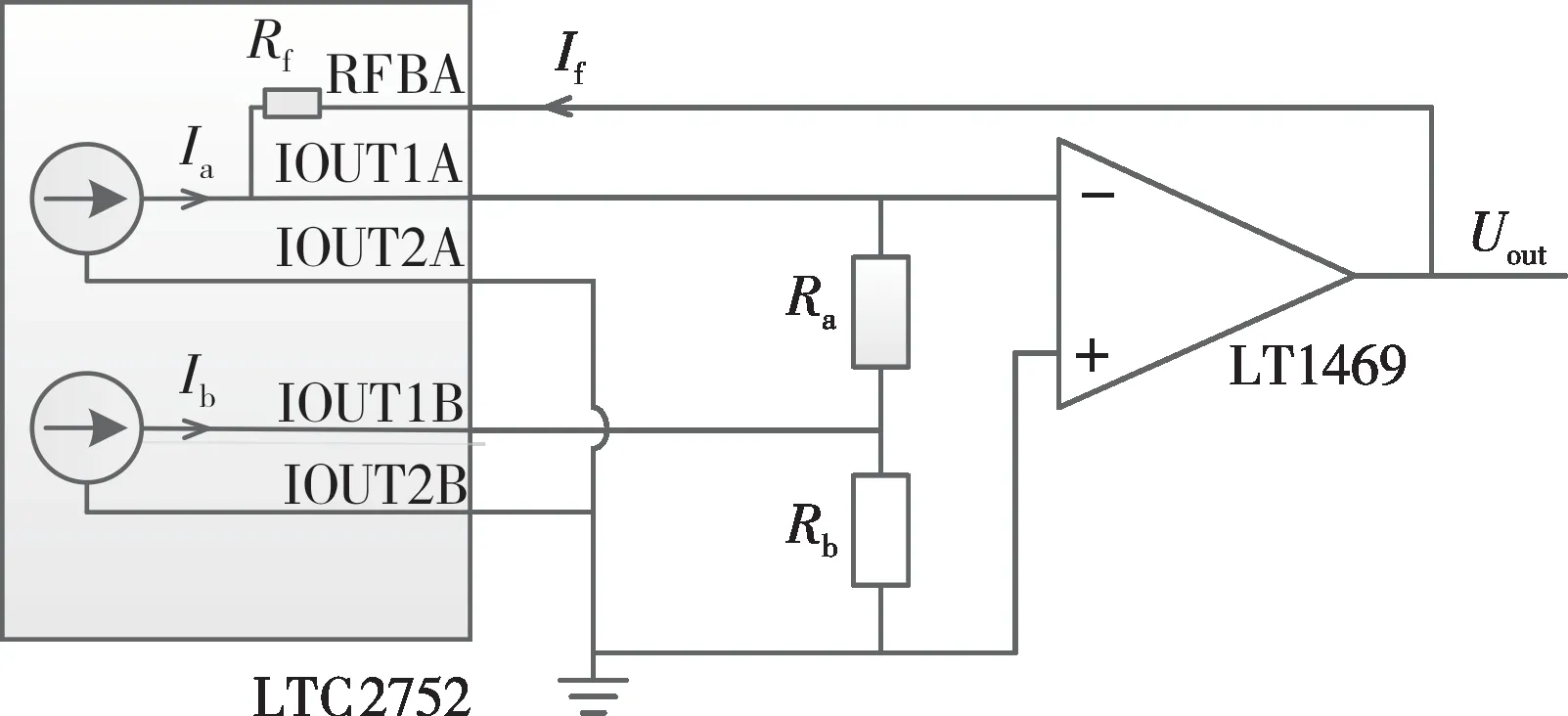
图3 双通道16位D/A转换原理框图

图3 中两个电阻阻值要求为Ra∶Rb=1 023∶1。MCU（微控制器）将DDS 输出波形值的高14 位输入到LTC2752 的端口A，低10 位输入到端口B。如式（2）所示，其输出Uout即是24位分辨率的模拟阶梯信号。Uout再经过运算放大器调理滤波后，即可输出高分辨率、高精度的平滑模拟信号。

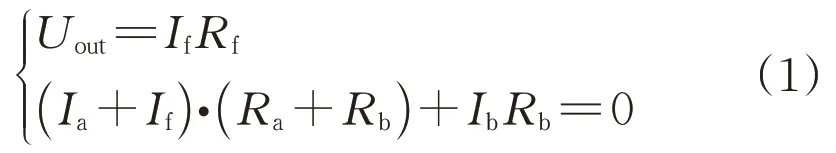
结合Ra=1 023Rb，推导可得：

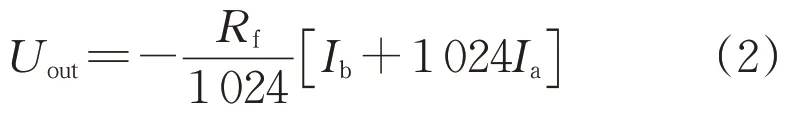
1.3 小电流信号的分段处理

OIML R46国际建议对电能表在小电流状况下的测量精度要求有明显提高。起动试验状态下仍需进行误差试验。本标准源为满足小电流输出精度指标，特增加10 mA电流档位。

控制、测量反馈取样电路如图4 所示，其中：A+和A-来源于数字功放的输出，B+和B-为电流输出接口；K1 和K2 分别为控制、测量反馈通路的切换开关，K3 为升流变压器的档位切换开关，由于仅考虑2个电流输出档位，此处采用单刀双掷的继电器；R1和R2为控制反馈电阻；R3和R4为测量反馈电阻。

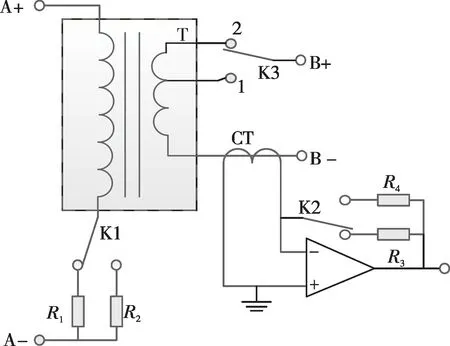
图4 电流控制、测量反馈电路

当输出电流大于10 mA 时，K1 和K2 分别切换到R1=2 Ω 和R3=50 Ω 侧，K3 切换到1 号档位；当输出电流小于10 mA 时，K1 和K2 分别切换到R2=20 Ω和R4=500 Ω侧，K3切换到2号档位。

为提高全量程测量精度，补偿电流互感器的非线性特性，一方面采用高精度微型零磁通电流互感器，其线性度可达0.02%；另一方面实现分4段（0～10 mA、10 mA～1 A、1～5 A、4～10 A）校准，在一定程度上模拟补偿电流互感器的非线性曲线，从而达到提高测量精度的目的。

1.4 数字功放

TDA8950TH 是恩智浦公司的一款高效率D类放大器，其功能是对前端高精度D/A 转换器输出的交流信号进行功率放大，以满足标准源输出功率的要求。

与线性放大器相比，D 类放大器的工作效率更高，这也意味着更小的功耗和体积、更高的输出功率，且由于不存在交越失真，D 类放大器输出波形的精度更高［10］。

TDA8950TH 的性能优越，工作效率高达90%，最大输出功率可达2×150 W，最大工作电压为±40 V，其250～450 kHz 的开关频率、零死区开关以及全差分输入信号为标准源的高精度输出提供保障。TDA8950TH 利用过温保护和过流保护，以及供电电压的过压、欠压、不平衡保护，全方位保证标准源的安全稳定可靠运行。

1.5 控制策略

针对输出信号高精度和高稳定度的要求，本系统采用以滞环控制为核心的动态环为内环、以加窗FFT 插值运算为基础的比例积分稳态环为外环的双环控制策略，兼顾标准源的响应速度、带载能力以及输出稳定性与精度，达到较为理想的运行效果。

2 内环控制策略

为尽可能提高标准源的响应速度，提升针对非线性负载的带载能力和高次谐波的输出精度，标准源的内环采用滞环控制策略。滞环控制是一种基于瞬时值反馈的控制方式，通过将反馈信号与给定信号之差输入到滞环比较器，并设定合理的滞环宽度使实际输入信号围绕给定信号作锯齿状变换，从而达到跟踪给定信号的目的。与其他闭环控制策略相比，滞环控制具有性能稳定、鲁棒性好、动态响应速度快、跟踪误差小、电路结构简单等优点［11］。然而滞环控制也存在着开关频率不确定的不足，这一方面会使得功率元件面临过热风险，另一方面会使得谐波频率分布广泛，难以通过低通滤波器滤除，给系统的EMC（电磁兼容）设计带来极大困难。因此，解决开关频率的不确定性是滞环控制研究的主要内容。

文献［12-13］均通过变环宽的方式来实现开关频率的基本恒定。在这类方法中，MCU利用给定信号或实测信号，根据不同算法计算环宽，通过D/A 转换器与运算放大器输出调整环宽。此类方案的结构复杂，对MCU的采样速度、运算能力要求很高。结合三角载波与滞环控制策略而构造出基于三角载波比较的滞环控制策略，辅以自适应前馈即能实现开关频率的基本稳定。

内环控制原理框图如图5所示，其中运算放大器U2、电阻Rn、电容C1 与MCU 的输出信号A构成了一个三角波发生器。当A点为正电压时，B点电压平滑下行；当A 点为负电压时，B 点电压平滑上行；当MCU控制A点电压按设定频率定时翻转时，在B 点将形成一个三角波。控制A 点电压的翻转频率，也就控制了滞环控制的开关频率。

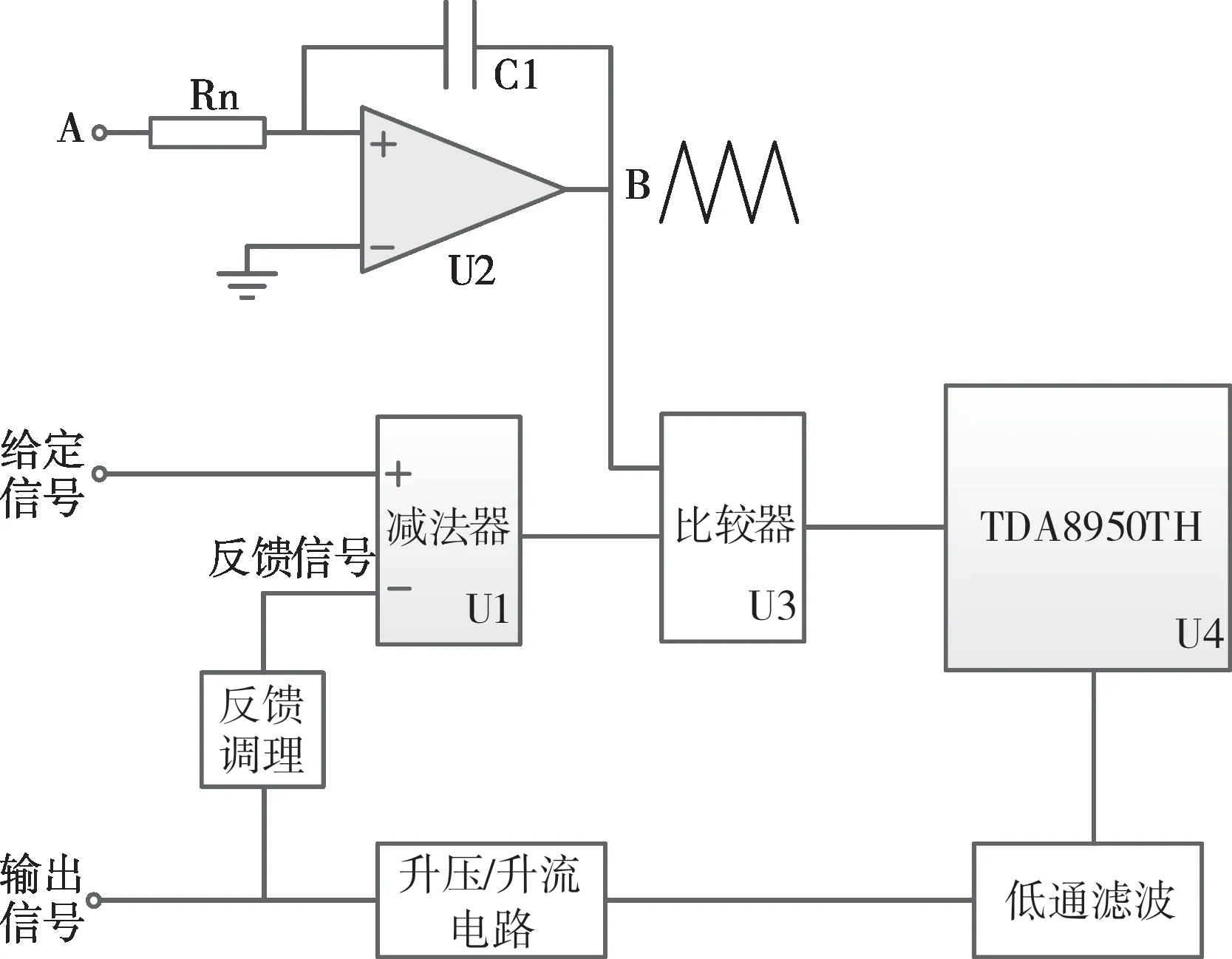
图5 内环控制原理框图

引入自适应前馈环节后，标准源能根据给定信号的幅值调节开关频率：在小电流时提升开关频率，以保证小电流信号的输出精度；在大电流时降低开关频率，以减小功耗，增强输出能力。

低通滤波环节由一组LC滤波电路构成，其主要功能是滤除TDA8950TH输出的高频载波信号，其截止频率可根据预设的最低开关频率而定。

升压/升流电路主要是由升压/升流变压器构成，具体根据该通道是电压通道或电流通道而定。

反馈调理是将输出信号调理成与给定信号相当的电压信号，根据该通道的类型采用分压或分流电路进行调理。

3 外环控制策略

比例积分控制是最经典的控制策略之一，具有算法简单、鲁棒性好、可靠性高等优点。当控制量为直流量或变化缓慢时，比例积分控制策略即能兼顾响应速度与跟踪误差，实现无静差控制。然而，要保证标准源的输出精度，首先要保证输出信号的测量与运算精度。因此，如何提高被控量的测量与运算精度是需要重点研究的内容之一。

基于傅里叶变换的谐波电参量测量是目前应用最广泛的一种方法。在计算畸变波形的谐波含量时，离散傅里叶变换是一种十分有效的分析方法，但是对信号的周期性和采样的同步性要求很高。当标准源输出频率的变化导致无法满足信号的整周期同步采样时，离散傅里叶变换所产生的频谱泄露和栅栏效应将导致谐波参数（频率、幅值和初相位）计算的不准确，从而影响谐波分析精度［14］。

加窗FFT 插值算法能有效抑制非同步采样时频谱泄露和栅栏效应带来的误差，且计算量小，易于实现，具有很强的工程使用价值。加窗FFT插值算法的基本原理是：加窗FFT 变换，获取被测信号中真实频率附近的峰值谱线，通过插值运算求得近似频点，再根据近似频点和峰值谱线求得近似的幅值和相位。不同的窗函数与不同的插值算法配合，相对应的会有一个固定的拟合多项式，通过预存储该拟合多项式，可大幅减少实时计算所需的时间开销［15］。

国内外学者提出了Hanning 窗、Hamming 窗、Blackman 窗、Blackman-Harris 窗、Nuttall 窗以及Rife-Vincent窗等窗函数，以及单谱线插值、双谱线插值、三谱线插值、六谱线插值等插值算法，这些加窗FFT 插值算法对于频谱泄露的抑制有一定作用，在不同程度上减小了谐波参数的计算误差，提高了准确度［16-20］。文献［21］给出了Hanning窗、Hamming 窗、Blackman 窗 的FFT 插值算法，修正公式简单，计算量小，但实际应用时精度不高。

着眼于标准源的工程实现，既要考虑算法的有效性和精度，又要考虑算法易于实现及快速实时性。在分析Rife-Vincent（I）窗旁瓣特性的基础上，经对比分析，拟采用5 项Rife-Vincent（I）窗FFT插值算法，结合双谱线插值修正公式来计算、分析标准源输出的基波及谐波分量，实现系统软件的外环控制。

3.1 Rife-Vincent窗特性

Rife-Vincent窗属于一种余弦组合窗，其离散时域表达形式w（n）为：

5项Rife-Vincent（I）窗的时域表达形式为：

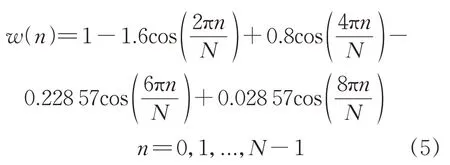
Rife-Vincent（I）窗的归一化对数频谱如图6所示，可以看出5项Rife-Vincent（I）的旁瓣渐进衰减速率为30 dB/oct（oct表示倍频程），旁瓣峰值电平达到-74.61 dB，其主瓣窄、旁瓣低且衰减速率快，适用于对谐波信号的加窗处理。

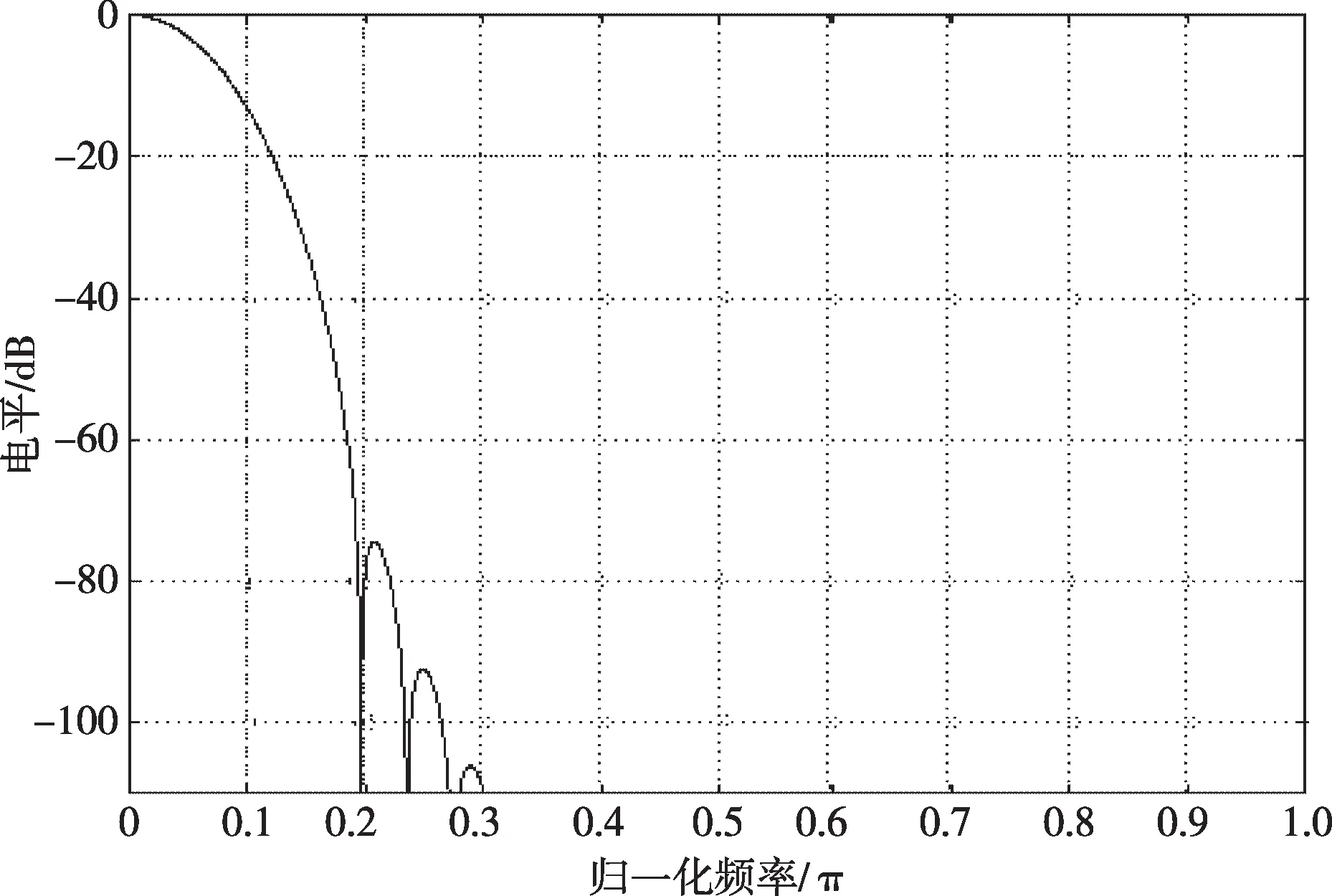
图6 Rife-Vincent（I）窗的归一化对数频谱

3.2 双谱线插值修正算法

非同步采样造成的栅栏效应会使得实际信号的频点落在两个离散频谱点之间，峰值谱所反映的频点和相位都会存在不可忽略的误差，此时需要对FFT的计算结果进行修正。

以包含多项整数次谐波分量的时域x(t)为例：

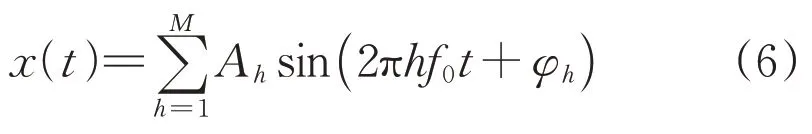
式中：M为最高谐波次数：h为谐波的次数；f0为基波频率；Ah和φh分别为基波或第h次谐波的幅值和初相角。

经过采样率为fs的数据采集系统后得到的离散序列x(n)为：

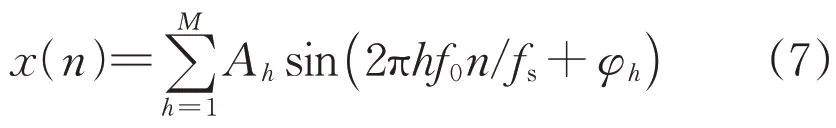
忽略负频点旁瓣的影响，对信号x(n)加Rife-Vincent（I）窗后的离散傅里叶变换结果XW（k）为：

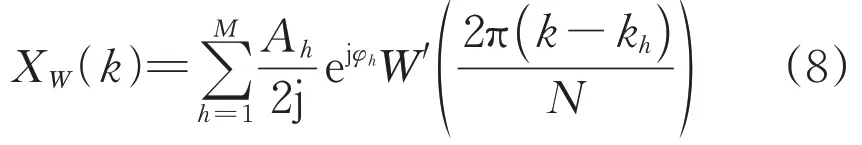
式中：kh为第h条谱线相对于Rife-Vincent 窗的谐波次数；k为输出指定谐波次数；W′为Rife-Vincent窗的连续频谱函数。

不失一般性，设需要测量的是第x（x≤M）次谐波，忽略其余谐波对x次谐波的影响，式（8）可简化为：

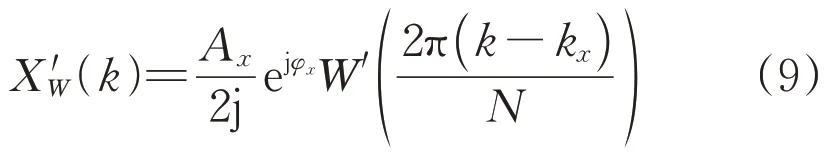
针对第x次谐波，在整周期同步采样的情况下，第x次谐波对应第kx根谱线，即可准确反映出第x次谐波的幅值和初相角。然而在非同步采样时，由于栅栏效应，第x次谐波的峰值频点很难正好落在抽样频点上，即在非同步采样时，kx一般不是整数。设在峰值频点附近抽样得到的幅值最大和次大频点谱线为kx1和kx2=kx1+1，可认为kx在kx1和kx2之间，即：

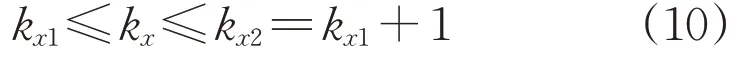
设这两个频点谱线所对应的幅值分别为ψ1=|X′W(kx1)|和ψ2=|X′W(kx2)|。由于0≤kx-kx1≤1，引入辅助参数λ=kx-kx1-0.5，λ∈[-0.5，0.5 ]，设ξ=(ψ2-ψ1)/(ψ2+ψ1)，则由式（10）经过变量代换可得：

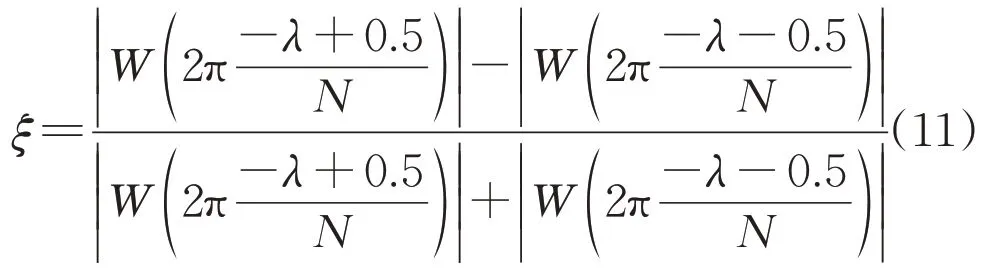
可记式（11）为ξ=f(λ)，则λ=f-1(ξ)。

设ω=2πk/N，则由式（4）可得：

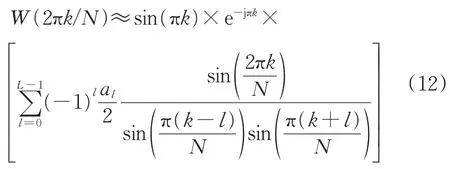
将k=-λ±0.5 代入式（12），由于| -λ±0.5|≤1，且N一般较大，因此有：

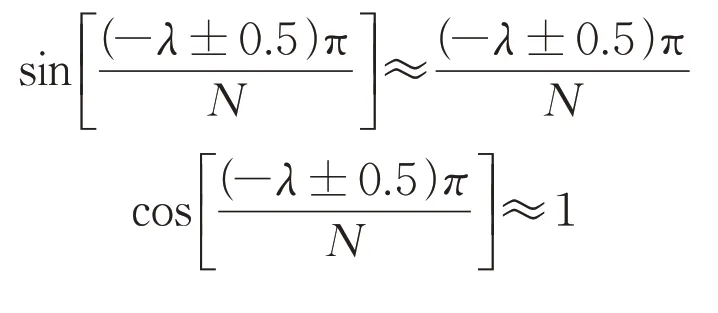
式（12）经过变换后可得：

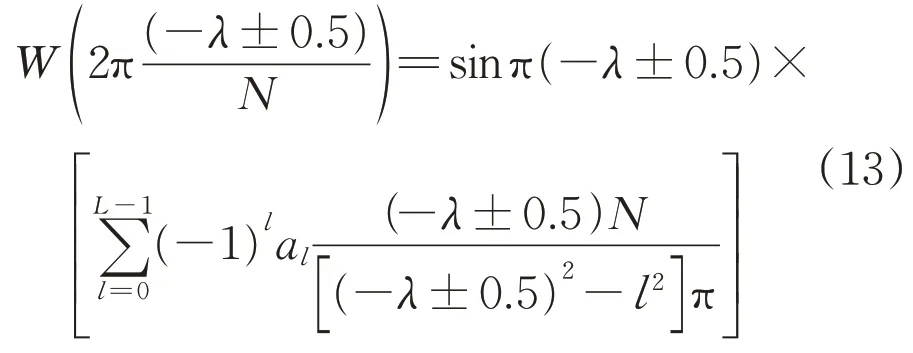
将式（13）代入式（11），在[ -0.5，0.5]范围内取一组λ，计算得出ξ，进行多项式拟合，即可得到函数λ=f-1(ξ)的逼近式。

根据kx1和kx2两个频点幅值计算ξ，根据λ=f-1(ξ)求得参数λ，则第x次谐波的修正频点fx计算式为：

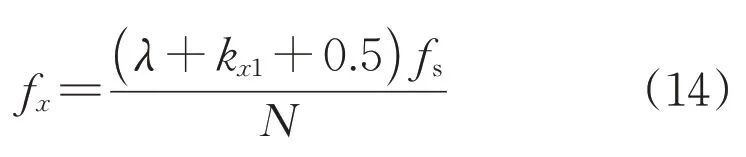
为修正峰值点的幅值，可对kx1和kx2进行加权平均：

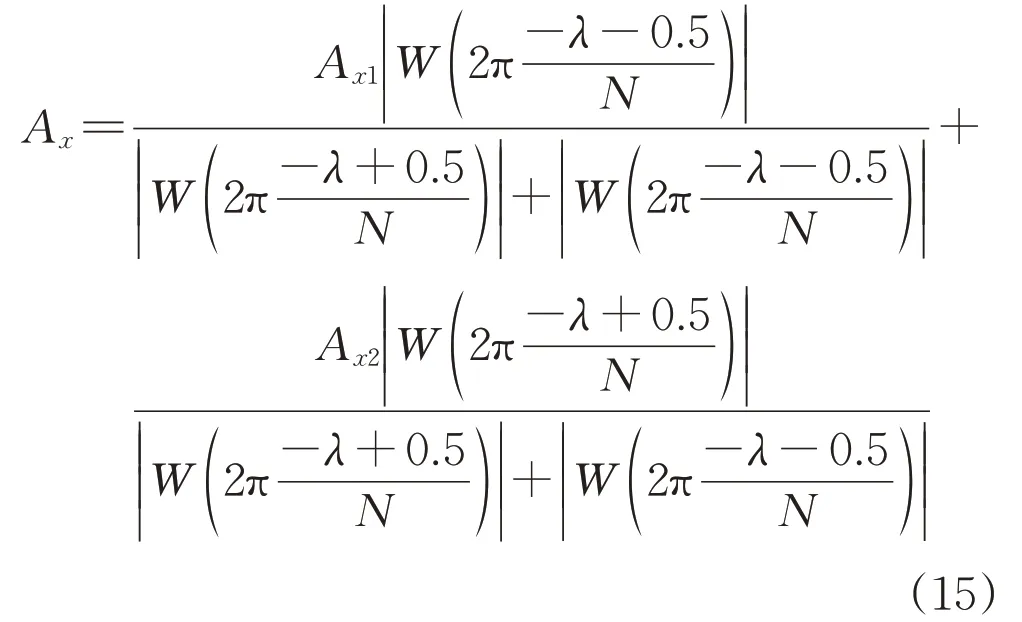
式中：Ax为x次谐波的幅值；Ax1和Ax2分别为第kx1和kx2根谱线的幅值。

由此可得：

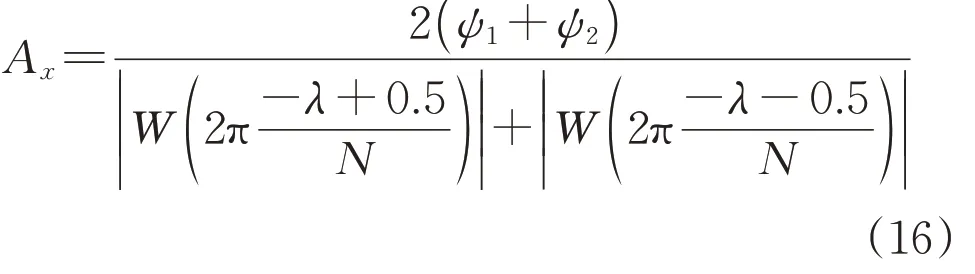
由式（9）和式（12）可得第x项谐波的相位修正公式为：

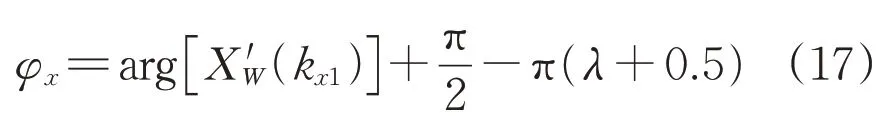
3.3 Rife-Vincent窗FFT插值运算过程

加窗FFT 插值算法的运算过程主要分为三部分，分别为输入信号的加窗、对加窗信号进行FFT以及对FFT 所得离散频谱作双谱线插值，以求得更加精确的谐波幅值与初相角。各部分的执行步骤如下：

1）信号加窗，对采样后的离散信号加Rife-Vincent（I）窗处理。

2）FFT，对步骤1）生成的加窗序列进行FFT，获得被Rife-Vincent窗截断后的离散频谱。

3）对离散频谱进行双谱线插值运算，获得谐波信号的向量值（包括频率、谐波幅值与初相角）。

4 试验结果

4.1 精度试验

本标准源设计的交流电压范围是0～264 V，交流电流范围是0～10 A。测量时，将本标准源的交流电压/电流输出端子与测量标准表直接相连。交流电压、电流精度试验测量数据见表1、表2，可以看出本标准源的输出相对误差绝对值均不大于0.04%，且电流回路的分段处理使小电流的输出精度得到明显提升。

表1 交流电压精度试验测量数据

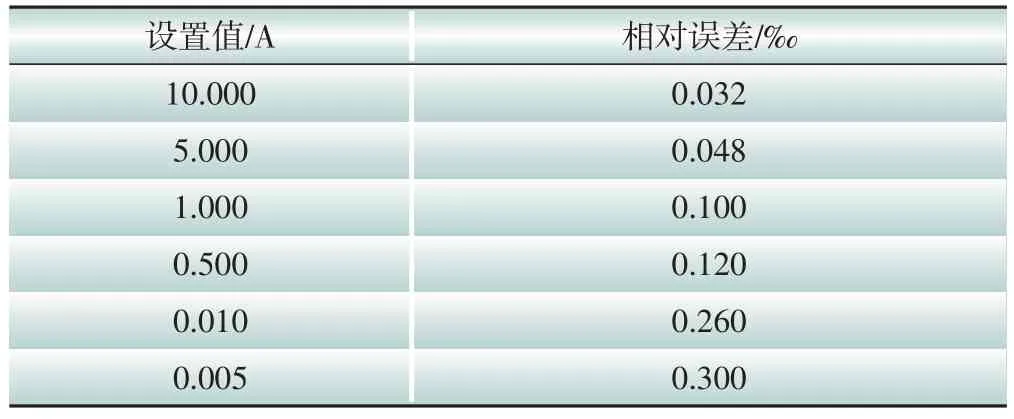
表2 交流电流精度试验测量数据

4.2 负载调整率试验

标准源的输出量要求不受外界干扰，尤其是外加负载干扰的影响，输出量随负载变化而产生的变化（即负载调整率）可体现出标准源的输出稳定性。交流电压、电流负载调整率测量数据见表3、表4，可以看出本标准源输出量的负载调整率不大于0.01%。

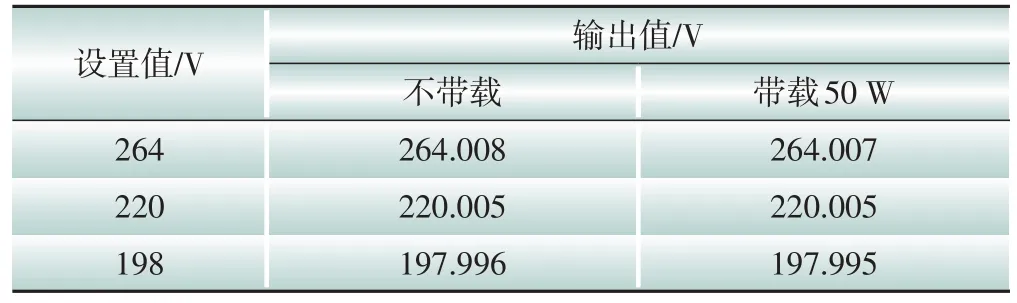
表3 交流电压负载调整率测量数据

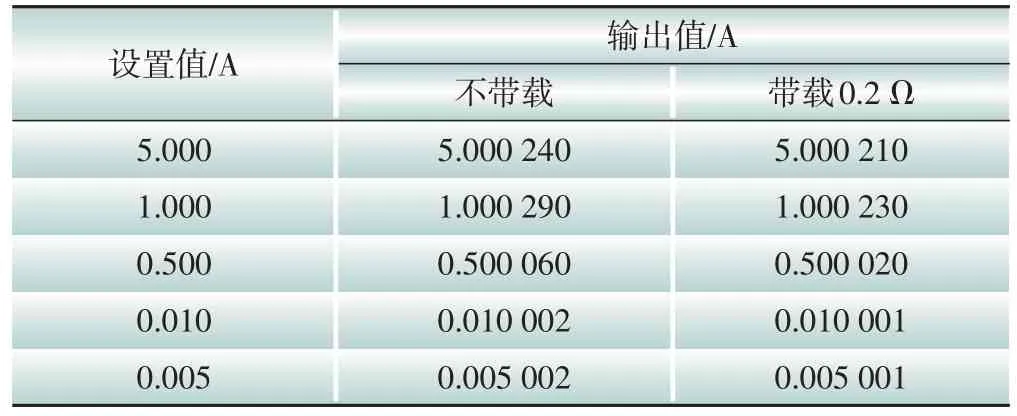
表4 交流电流负载调整率测量数据

4.3 非线性负载带载能力试验

以典型六脉冲整流负载为例，验证标准源电压输出端的非线性负载带载能力。电压输出220 V，电流0.1 A，标准电压输出端波形如图7 所示。在电流瞬时突变瞬间，以定频滞环为核心的内环控制能快速响应，使得电压波形保持平稳，并无畸变。

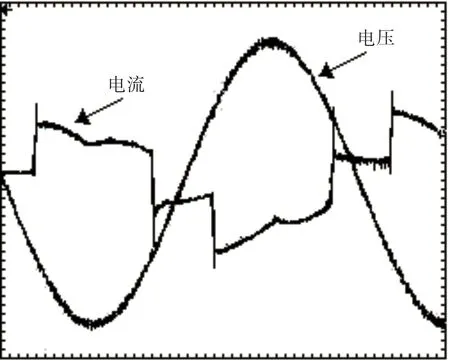
图7 标准电压输出端波形

4.4 负载突变影响试验

标准电压输出端负载突变波形如图8所示。在标准源电压输出端负载投入瞬间，产生的冲击涌流远高于平稳状态下的电流峰值，在此期间电压波形保持平稳，并未产生畸变。

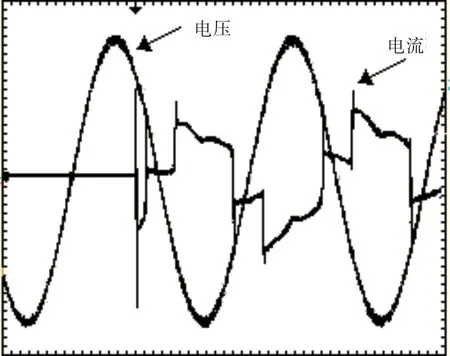
图8 标准电压输出端负载突变波形

5 结语

基于传统程控标准源，在DDS、D/A 转换、功率放大、小电流处理机制、控制策略等方面进行优化，提出以定频滞环为核心的动态内环和以Rife-Vincent（I）窗FFT 插值为基础的比例积分稳态外环相结合的双环控制策略，兼顾标准源的响应速度、带载能力、输出稳定性与精度，有效抑制了频谱泄露和栅栏效应，提高了反馈谐波分量测量的精度。

试验结果表明，本文所提方案可有效增加标准源电压通道的带载能力，大幅提高标准源输出信号尤其是小电流信号的稳定性和精度。