基于快速核学习的新能源高渗透电网频率风险评估
2022-04-26王冠中王龙飞王博文叶承晋
董 炜,华 文,王冠中,王龙飞,王博文,叶承晋
(1.国网浙江省电力有限公司电力科学研究院,杭州 310014;2.浙江大学 电气工程学院,杭州 310027)
0 引言
建设以新能源为主体的新型电力系统是我国实现碳达峰、碳中和目标的主要方式。然而,以低惯量的新能源发电设备替代同步机作为电力系统的主要电源,导致新型电力系统在功率扰动后频率响应特性朝着不利于系统的方向改变,影响频率保护动作的作用,严重时可引起连锁故障,威胁电网安全稳定运行[1-3]。针对上述情况,准确评估功率扰动后新型电力系统的频率响应轨迹特征关乎系统的安全稳定[4]。
电力系统在受到功率扰动后,动态频率关于额定工频的最大偏移量和动态频率轨迹上点的变化率受到系统调度和控制部门的重点关注,原因在于上述两个频率特征对于频率保护动作的影响最大[5]。例如,根据实际电网低频减载启动的条件,一般要求频率低点高于49.1 Hz,因此可将频率波动低于49.1 Hz 视作运行风险。此外,《电力系统安全稳定导则》也对此做出相应规定,即在停电恢复过程中注意有功功率的平衡,防止系统频率大幅波动。上述背景都要求针对频率动态特征进行深入分析与定量研究。
目前主要有三类频率动态特征的分析方法,分别是基于简化模型的解析法[6]、机电暂态详细仿真法[7]和基于人工智能的方法[8]。其中,机电暂态详细仿真法分析准确但计算效率低,一般被用作比较对象而不作为实际系统运行中的分析方法,适用于验证其他两类方法的准确性,因此,这里主要比较简化模型和人工智能两类方法的区别。简化模型法的基本思路是将系统的频率动态用降阶的同步机和新能源动态模型进行分析,一般发电设备模型为阶数不超过2的PID(比例-积分-微分)控制结构,重点分析系统惯性和阻尼对系统平均频率偏移量的影响。文献[6]针对多机系统频域模型提出了主导系统频率特征的共模分量,是对系统平均频率概念的推广,可对频率偏移量与平均变化率进行比较准确的解析估计,但是没有考虑系统电压分布、功率扰动位置等因素对频率特征的影响[9-12]。另一方面,随着以统计学习和深度学习为代表的人工智能算法的快速发展,相应方法也被引入电力系统的频率特征分析中,例如文献[9]提出将蒙特卡洛模拟与神经网络相结合的频率特征分析方法,利用神经网络提高蒙特卡洛模拟的计算效率,进而实现了高效率的频率最大偏差越限风险评估。然而,神经网络,特别是深度学习,由于网络层次多,学习算法中待定参数较多,容易出现模型训练难以收敛的现象,即难以确定是由于网络结构的适应性问题还是优化算法的参数设置问题而导致无法收敛。
为进一步提高频率特征评估方法的效能,本文采用简化模型与人工智能相结合的思路,提出基于快速核学习的系统频率风险评估方法。首先,根据已有共模频率相关理论,将解析的频率偏差量和变化率作为学习算法的一部分输出,有助于减少学习算法的数据维数,进而降低训练模型的复杂度。其次,利用多项式核学习的正则项可通过核矩阵广义逆进行快速估计的性质,直接由有限但相互独立的输入数据获取训练结果,避免深度学习参数寻优过程中的收敛性问题。所提方法不依赖训练数据量,也适用于大电网实际运行数据的快速学习。最后,利用仿真数据验证了所提方法的有效性。
1 基于共模频率的解析结果
鉴于所提基于快速核学习的频率风险评估方法是通过直接输入共模频率解析结果来减少学习算法的输入数量,进而减小训练模型的复杂度,因此首先简要介绍基于共模频率的频率最低点和平均变化率的解析量化结果[6]。
文献[6]在忽略电压波动、调速器死区等非线性环节以及低频减载非线性动态等的基础上,采用文献[13]提出的共模和差模频率概念中的共模分量来模拟全系统的频率轨迹。具体地,当系统中同步机和新能源等发电设备的频率-有功功率的单输入单输出传递函数(忽略了电压动态的影响)分别用Gi(s),i=1,…,n来描述时,在负荷发生阶跃扰动时,系统的共模频率响应为:
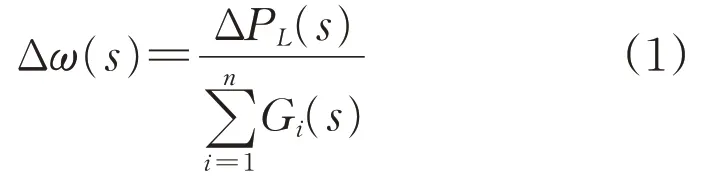
式中:Δω(s)为系统的共模频率;s为拉普拉斯算子;ΔPL(s)为系统全部负荷扰动总量(忽略扰动位置的影响)。
共模频率分量的推导过程详见文献[6,10],这里仅对主要思路进行概括。若发电机所在节点i的频率微增量Δωi(s)和功率微增量ΔPi(s)的传递函数表示为-Gi(s)Δωi(s)=ΔPi(s),那么保留全部发电机节点的系统传递函数矩阵可表示为:

式中:G(s)=diag(Gi(s))为对角矩阵;ΔP(s)和Δω(s)分别是由ΔPi(s)和Δωi(s)组成的列向量;L为节点导纳矩阵(含平衡节点);ω0为额定工频。
共模频率的动态响应式(1)则是在系统传递函数矩阵式(2)的基础上进行的化简和变量替换,在频率动态响应这个时间尺度上,具有传递函数矩阵式(2)主导特征轨迹的性质,因此可反映系统的频率响应特征[10]。
文献[6]进一步将Gi(s)简化为仅代表惯量、阻尼和调速器作用的二阶模型,则系统共模频率响应可表示为统一结构模型:
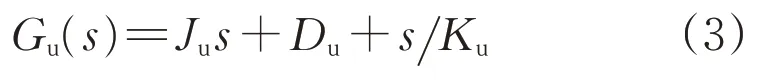
式中:Ju、Du、Ku为系统中发电设备二阶近似模型对应参数的总和。
据此,可定义出反映频率最低点的跌落深度系数α以及反映频率平均变化率的跌落坡度系数Jz:
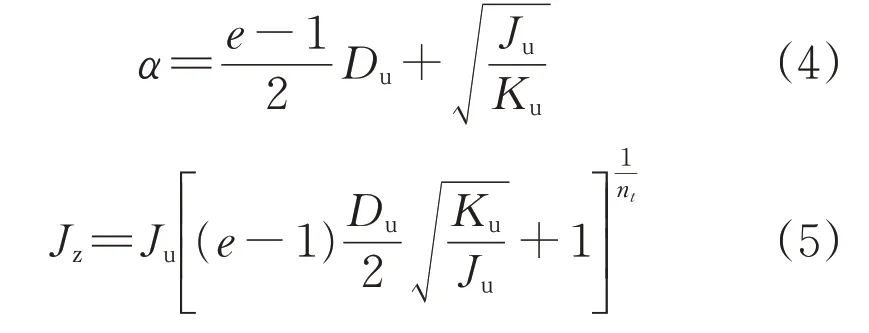
式中:nt为整数,一般可取值为3。
本节中的跌落深度系数α和跌落坡度系数Jz将作为后续基于快速核学习的频率特征评估的部分输出量,具有降低数据维数的作用。具体地,扰动功率(标幺值)除以跌落深度系数α的结果被用来近似频率最低点,扰动功率(标幺值)除以跌落坡度系数Jz的结果被用来近似频率跌落速度。频率低点和跌落速度一般作为判定频率稳定的主要指标。
2 快速核学习算法
2.1 核学习算法
核学习算法是对一类基于核函数的学习方法的统称,主要类型分为SVM(支持向量机)和SVR(支持向量回归)等,其主要特征为学习所得的模型f(x)总能表示成核函数κ(xi,xj)的线性组合。
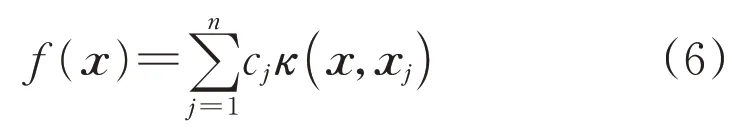
式中:cj为待训练的参数;列向量xj∈Rd和x∈Rd分别表示训练集和测试集中的输入数据,Rd代表实数空间中的d维列向量。
本文所采用的多项式核函数可表示为[11]:

式中:s≥1为多项式的次数。
式(7)中的函数在满足下面核矩阵K半正定的条件时,才能作为核函数被使用。

式(9)中的正则项可在希尔伯特空间是无穷维空间时确保优化问题存在唯一解。而当希特波特空间为有限维空间时,可通过调节参数λ的大小来控制空间的维数以实现协调目标数据分布方差和偏度的目的。
针对多项式核函数的研究表明[14],当采样数量m和多项式次数s增加时,正则项系数λ可以指数或以任意速度进行衰减。基于上述理论发现,文献[14]直接在式(9)中忽略正则项,提出一种比经典核学习方法具有更好收敛性的快速核学习方法。
2.2 快速核学习算法
快速核学习算法主要分为两大部分,第一部分的目的在于给定多项式次数s后确定学习模型,第二部分是分析多项式次数s的确定方法。
2.2.1 第一部分具体步骤
2)令n=(C为组合数)表示从测试集中选取的中心点的数量,以及一组相互独立的输入数据来代表输入数据空间的中心点。
4)令测试集的输出向量为y=(y1,…,ym)T,训练模型式(6)中的待定参数组成向量为c=(c1,…,cn)T,则有c=pinv(Am,n)y,其中,pinv代表广义逆运算。
快速核学习算法的第一部分利用给定的多项式次数s,仅通过一次广义逆运算即可得到训练结果fZ,s,避免了参数寻优过程中可能出现的不收敛问题,对于核学习算法的计算效率具有明显的提升作用。但是,对于如何确定多项式次数s尚缺乏论述。
2.2.2 第二部分具体步骤

快速核学习算法的整体步骤是通过两部分的交互迭代最终得到多项式次数s′以及对应的训练模型。实际应用中应注意选取输入数据中心点时要确保相互独立,在输入矩阵维数较高时,可采用文献[15]中的投影算法从大量输入数据中快速找到一组彼此之间距离最大的正交基。
本节主要介绍了核学习算法的基本形式以及快速核学习算法的基本思想和具体步骤,下面主要介绍基于快速核学习的频率风险评估方法,侧重介绍输入和输出数据的构建,以及核学习系统的具体组成方式。
3 基于快速核学习的频率风险评估方法
基于快速核学习的频率风险评估模型结构如图1所示,主要包含机电暂态仿真系统和核学习模型两部分,其中,机电暂态仿真系统负责产生足够的训练集数据用于训练核学习模型中的待定参数;核学习模型采用第2章中的多项式核函数进行构建,并将第1章中的共模频率解析结果直接作为输出的一部分。

图1 频率风险评估模型结构
图1所示风险评估模型的具体应用过程如下:
1)类似电力系统模型中的参数标幺化,首先将不同分布范围的数据折算到统一的区间内,便于反映如功率、电压以及其他整数变量对频率特征的影响。
2)将电力系统中少量同步机的设备参数和有功扰动功率数值直接输入到共模频率解析计算环节,得到频率低点和下跌速度的估计值(系统中新能源机组认为不提供频率支撑服务)。
3)主要针对共模频率理论中未计及的励磁环节以及PSS(电力系统稳定器)的分布位置信息(总数以及全部发电机节点数量的方差、峰度和偏度)和有功扰动功率数值输入核学习模型,其中PSS采用同一结构以便于分析规律,并利用机电暂态仿真曲线中的频率低点以及下跌速度的测量值训练核学习系统参数。
4)最后,直接利用核学习模型估计PSS 不同分布情况和功率扰动不同数值下的频率低点和下跌速度,并与预设的两个安全阈值做比较,若阈值没有被超过,则输出结果为1,代表着系统频率安全稳定条件得到满足;否则输出为0,代表系统设置不满足频率安全稳定需求。
4 仿真分析
4.1 IEEE 39节点系统设置
算例采用IEEE 39 节点系统进行仿真分析,额定频率为60 Hz,含10 台同步发电机,其中G1—G9 为汽轮发电机,G10 为水轮发电机,表1 给出各发电机简化模型的参数设置情况,表中并未考虑阻尼的作用。负荷采用恒阻抗负荷简化分析。此外,G1实际代表外电网,因原始容量参数太大导致影响频率动态过程,故在此将其容量设置为普通发电机容量。其余参数同文献[6]。
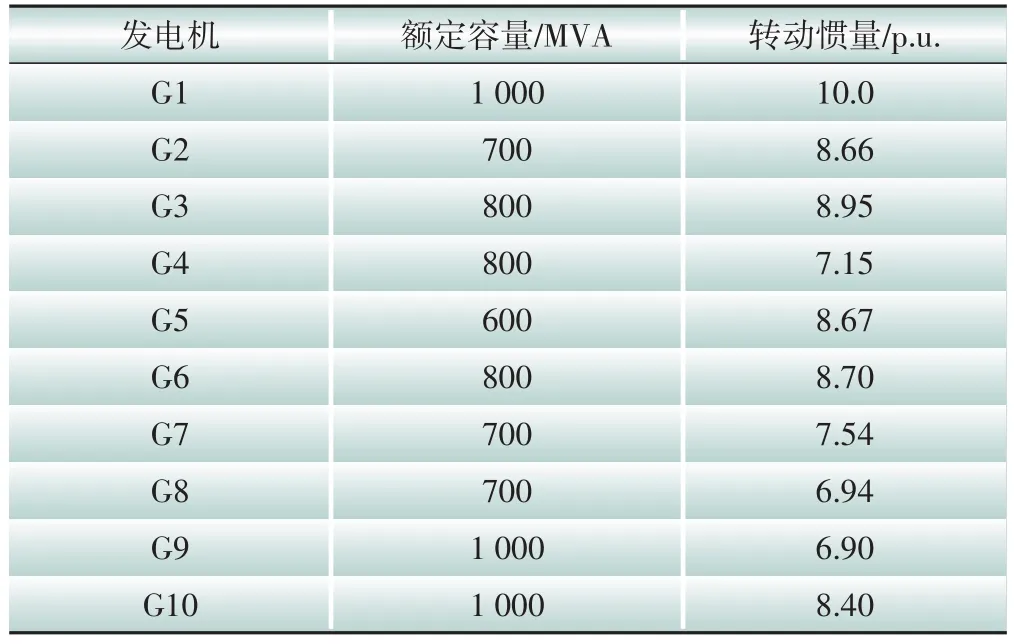
表1 各发电机简化模型参数
采用PSS 2B型号的通用PSS反映电压控制对频率动态的影响,通过改变安装位置和数量可产生训练集数据用于核学习系统参数训练。
4.2 核学习算法有效性验证
设置频率低点和下跌速度的阈值分别是49.1 Hz和0.9 Hz/s,功率扰动(增大负荷功率)在320~1 000 MW之间随机分布,PSS安装数量在0~9之间随机分布(水轮机不设置PSS)。利用基于MATLAB 平台的Simulink 仿真环境对IEEE 39 节点系统进行仿真分析,产生150组频率低点和下跌速度结果作为训练集输出,另外150组数据用于测试集。按照第2章的方法流程,将训练集数据分为100 组和50 组两部分,第一部分用于训练核学习中多项式系数,第二部分用于确定最优的多项式次数。按照第3 章的输入设置,输入包括PSS 的数量、方差、峰度和偏度,共4个维度,所得多项式次数为3次。
典型场景的频率动态为:根据表1 中的数据,将PSS 加入到3 台700 MVA 的机组电压控制环节中,并在IEEE 39节点中加入0.6 p.u.的负荷扰动,得到加装PSS前后频率下跌的数值分别为0.26 Hz和0.23 Hz。受限于文章篇幅,其余场景的结果统一用学习方法的误差进行描述。
表2结果验证了本文所提方法的有效性。无论测试集还是训练集,本文所提核学习方法的正确率均达到90%以上,说明该方法没有出现过拟合问题。表2中的正判错误率代表原本输出为1的情况被错判为输出为0,反判错误率与之相反。此外,无论在训练集还是测试集,正判错误率均低于反判错误率,主要原因是考虑PSS 配置情况以后,实际频率低点一般会高于共模频率理论的估计值,而电压控制动态会降低负荷功率对发电机转子动态的影响程度;同时,核学习算法由于仅采用一次迭代,当所用数据中频率低点较高时,训练结果偏高,导致误差表现为高估频率低点的情况较多。

表2 基于快速核学习算法的评估效果%
5 结语
本文提出基于快速核学习算法的频率风险评估方法,主要分析了发电机电压控制动态对频率低点和下跌速度的影响。所提核学习算法仅需一次矩阵广义逆运算即可得到训练参数,相比以神经网络为代表的学习方法,它不受模型训练参数收敛性的影响,具有方便易用的优势。此外,本文所提方法主要针对在线运行的应用场合,以解析指标为基础,辅之以解析结果与仿真结果之间误差的机器学习结果,以增强频率特性评估的准确性。因此本文的重点不仅在于机器学习的方法,更在于所采用的指标以及对指标误差来源的分析。与其他文献中的神经网络方法[8-9]相比,本文方法适用于在线场景,而其他方法适用于离线场景,并且本文方法的数据量小、收敛性好,可以结合少量仿真结果对电网结构变化后的频率解析评估结果做出及时的修正。
