基于风资源评估不确定性分析的风电有效出力计算模型

魏媛，李涛，赵振宙，胡朝阳，燕敏飞，袁泉，许帅

(1.中国电建集团河南省电力勘测设计院有限公司，郑州 450007；2.河海大学能源与电气学院，南京 21100)

在碳达峰、碳中和目标背景下，风力发电装机规模快速增长，我国能源生产和消费面临重大转型，构建新一代电力系统是实现这一转变的关键步骤[1]，大力发展清洁能源，能够有效减少温室气体排放，促进环境保护，对改善能源结构和保障能源安全具有重要意义。

由于风电出力存在波动性、随机性的特征，它和传统火电、水电出力特性差异性较大，采用传统出力曲线的方法分析风电特性存在较大的困难。

刘宝林[2]等根据已并网运行的风电场，对风电场全年出力数据进行处理，得出各出力区间的概率值，在风电接入系统技术参数选择、区域电力平衡计算方面进行应用。

程临燕[3]等在现有风电和光伏的全年出力数据的基础上，结合风电和光伏规划比例得到风光互补全年出力数据，在区域消纳新能源分析中进行应用。

上述研究的基本思路是结合已建成项目出力历史运行数据进行分析，通过概率模型研究，提出规划项目的出力特性，进而对区域内新能源消纳进行分析。但资源禀赋、设计方案不同的风电场出力特性必定存在差异，该方法简化了不同风电场之间的差异性。此外，在实际工作中收集已建成项目历史出力数据也存在以下问题：1)已建成项目发电量历史数据涉及企业保密因素，数据难以收集；2)建成项目全容量并网时间不足1年以上，或项目发电量逐时数据管理不完备，满足要求的完整年逐时发电量历史数据完整性较差；3)规划项目区域周边无已建成在运行风电场项目，该分析方法失效。

此外，已建成项目只针对特定年份下的实际历史出力数据，受风电场风速年际变化影响非常明显，采用以上方法分析未考虑风电场年际变化因素。

为解决上述难点，更准确评估规划风电场项目出力特性，采用测风塔实测1年(即8 760 h)及以上逐时数据，在风电场机位排布方案的基础上，采用流体计算CFD(Computational Fluid Dynamics)模型，提出基于风资源评估不确定分析方法的风电有效出力计算模型，为风电场接入系统技术参数选择、风电参与电力平衡计算等方面提供理论依据。

1 风电场出力特性指标

受地理位置及资源条件分布影响，不同区域、同区域不同设计方案的风电场项目出力特性差异较大，结合风电场项目参与区域电网电力电量平衡研究方法，风电场出力特性指标[3]如图1所示。

图1 风电场出力特性指标

(1)风电全年持续出力曲线：将风电场全年每小时的出力由大到小排序，该单调递减曲线可以反映风电出力高于(或低于)某一数值的概率。

(2)风电有效出力：根据风电全年持续出力曲线，将风电概率99%～95%对应的风电出力作为有效风电出力，即风电出力大于有效风电出力的概率为1%～5%，对应风电出力小于或等于有效风电出力的概率为99%～95%。图1中表示该风电场的有效出力为76%，主要用于风电送出工程设备选择和电网消纳风电能力计算。

(3)风电有效平均出力：在风电全年持续出力曲线中，以风电有效出力为界限，去掉大于风电有效出力的值，并对剩余值求平均作为风电有效平均出力。该值的含义在于考虑风电调峰后风电的实际输出水平。

(4)风电保证出力：取风电出力概率95%对应的风电出力，定义为风电保证出力，即风电出力大于风电保证出力的概率为95%。

2 不确定分析方法

2.1 超越概率分布

假设风电场发电量概率密度函数f(QNet)符合正态分布，其超越概率函数F(QNet)可采用正态分布的累计函数进行表示：

(1)

式(1)中，QNorm为折减后的发电量，QNet为考虑不确定因素后的发电量；σ为风速序列的不确定性标准差；f(QNet)表示发电量为QNet的概率；F(QNet)表示发电量大于等于QNet的概率。

定义Pi表示置信率i%，QNet,i=F-1(i%)称为Pi置信率下的发电量水平。例如QNet,50=F-1(50%)为P50置信率下的发电量，按照正态分布特性，有QNet,50=QNorm。

假设某一风电场项目，折减后的发电量QNorm=2 000 万kW·h，对于总的不确定性标准差σ分别为5%、10%时，风电场发电量概率密度函数f(QNet)及超越概率函数F(QNet)如图2所示。

图2 风电场发电量概率密度函数及超越概率函数

图2中不同风电场，对于折减系数相同的风电场项目，不确定性标准差σ越大，发电量概率函数分布越宽大，其大于P50概率下的发电量越小，小于P50概率下的发电量越大，反映出风电场风险逐渐增加[4]。P90，10%表示不确定性标准差σ为10%时的P90置信率下的发电量为1 658万kW·h，结果小于P50概率下的发电量。

2.2 发电量折减因素

在风电场发电量评估过程中，风电场年上网电量是在理论发电量QAE的基础上，考虑空气密度、尾流修正、风机利用率、功率曲线、叶片污染、控制和湍流强度、以及风电场内能量损耗和气候等因素的影响[5]，对其进行修整，得出风电场折减后的净发电量QNorm。

表1为风电场项目发电量折减因素表，根据发电量折减的各项因素，计算总折减系数及风电场的上网电量，具体公式如下：

(2)

式(2)中，发电量折减的各项因素li通过表1进行确定。

2.3 发电量不确定性因素

在风电场风资源评估过程中有很多不确定性因素来源，而且这些因素大多与风速存在一定关系，为准确评估发电量不确定性，常使用敏感因子λv-P将风速不确定性转化为发电量不确定性，该数值与地形复杂程度存在一定关系，地形越复杂、风速越低，该值越高，常规取值为1.5～3.0之间。

计算总的不确定性时，需要对各不确定性分量进行几何求和，主要涉及测风塔测量、历史数据、垂直外推、长期风况变化、风电场空间变化和耗损不确定性等[6]，各不确定性分量之间往往存在着某种联系，但这种联系关系较小，可认为各不确定性分量之间相互独立，表2为风电场发电量不确定性因素表，总的不确定性为几个不确定分量的乘积开方，即：

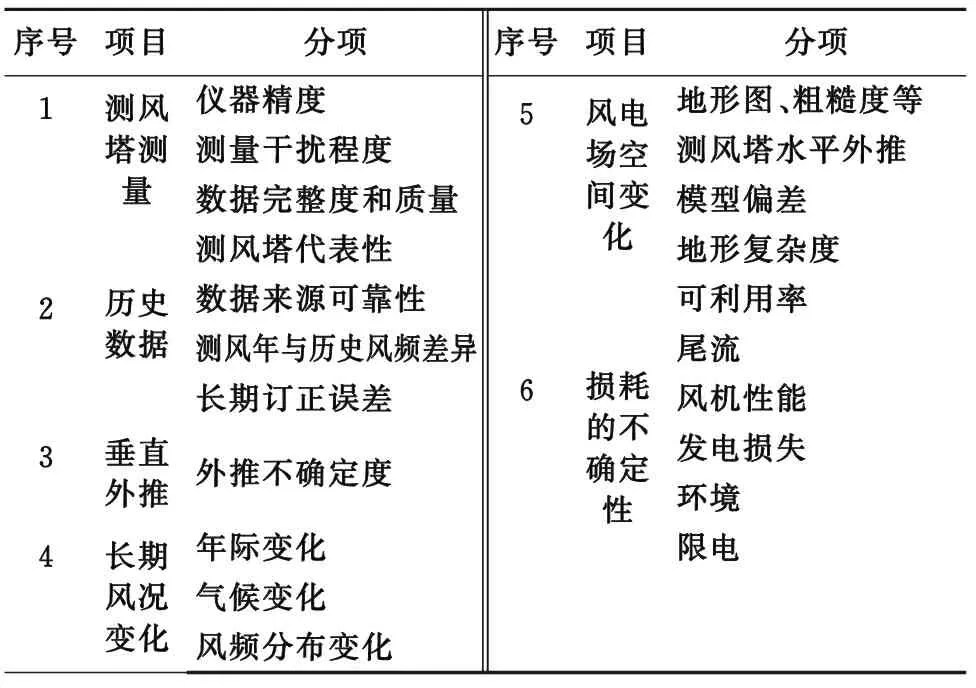
表2 风电场发电量不确定性因素

(3)

式(3)中，σi为单一不确定因素的标准差，σ为总的不确定性标准。

3 算例及分析

3.1 典型风电场项目

为研究不同区域和不同方案的风电场出力特性，在河南省选取新乡市、驻马店市和平顶山市进行分析，选取风电场设计参数如表3所示。不同区域风电场风资源月变化如图3所示。

表3 风电场设计参数

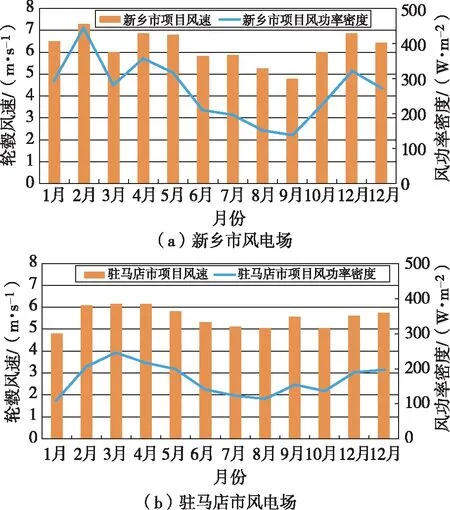
图3 不同区域风电场风资源月变化图

在风电场风资源评估过程中，采用至少满1年以上的测风塔逐时数据进行分析，根据附近气象站及中尺度数据完成测风数据代表性分析，订正出一套能反映风电场长期平均水平的代表性风资源长系列数据。该方法能够反映风电场长期出力特性，减少因特定年份风速变化引起风电场出力评估差异。从图3中可以看出，河南省三区域风资源整体呈现春冬风速大和夏秋风速小的分布规律。

3.2 不同区域出力分析

通过流体计算CFD模型[7]，计算风电场逐时理论发电量QAE，对项目进行折减和不确定性分析，确定项目逐时出力，绘制全年相对出力概率曲线图，不同区域风电场全年相对出力概率曲线如图4所示。

图4 不同区域风电场全年相对出力概率曲线

图4中三个风电场项目全年相对出力概率曲线具有相似性，风电场出力特性曲线为倒s型曲线，风电场出力概率越大，风电场相对出力越大。表4统计结果显示不同区域风电场95%概率下的风电场有效出力在72.6%～76.7%之间，区域中风资源较高的区域有效出力也相对较高。

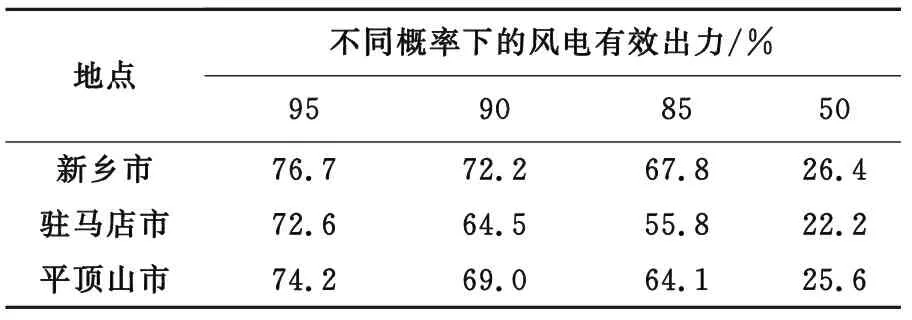
表4 不同区域风电场全年相对出力概率 %

不同区域风电场的出力特性曲线的曲率存在较大差异，即不同风电场在不同概率下的相对出力变化较大。结合三个典型风电场项目的风资源评估成果，风电场出力特性不仅受风资源条件影响，还与风电场设计方案存在关系。

3.3 风电场昼夜出力分析

图5为新乡市典型风电场全年昼夜相对出力概率曲线，表5为新乡市典型风电场昼夜相对出力概率。从图5及表5中可以看出新乡市风资源昼夜的风电场有效出力差异较大，夜间95%概率下有效出力为78.0%，白天95%概率下有效出力为74.5%。随着概率值的减小，新乡市风电场的有效出力明显下降，全年50%概率下有效出力为26.4%，白天有效出力仅为20.2%。

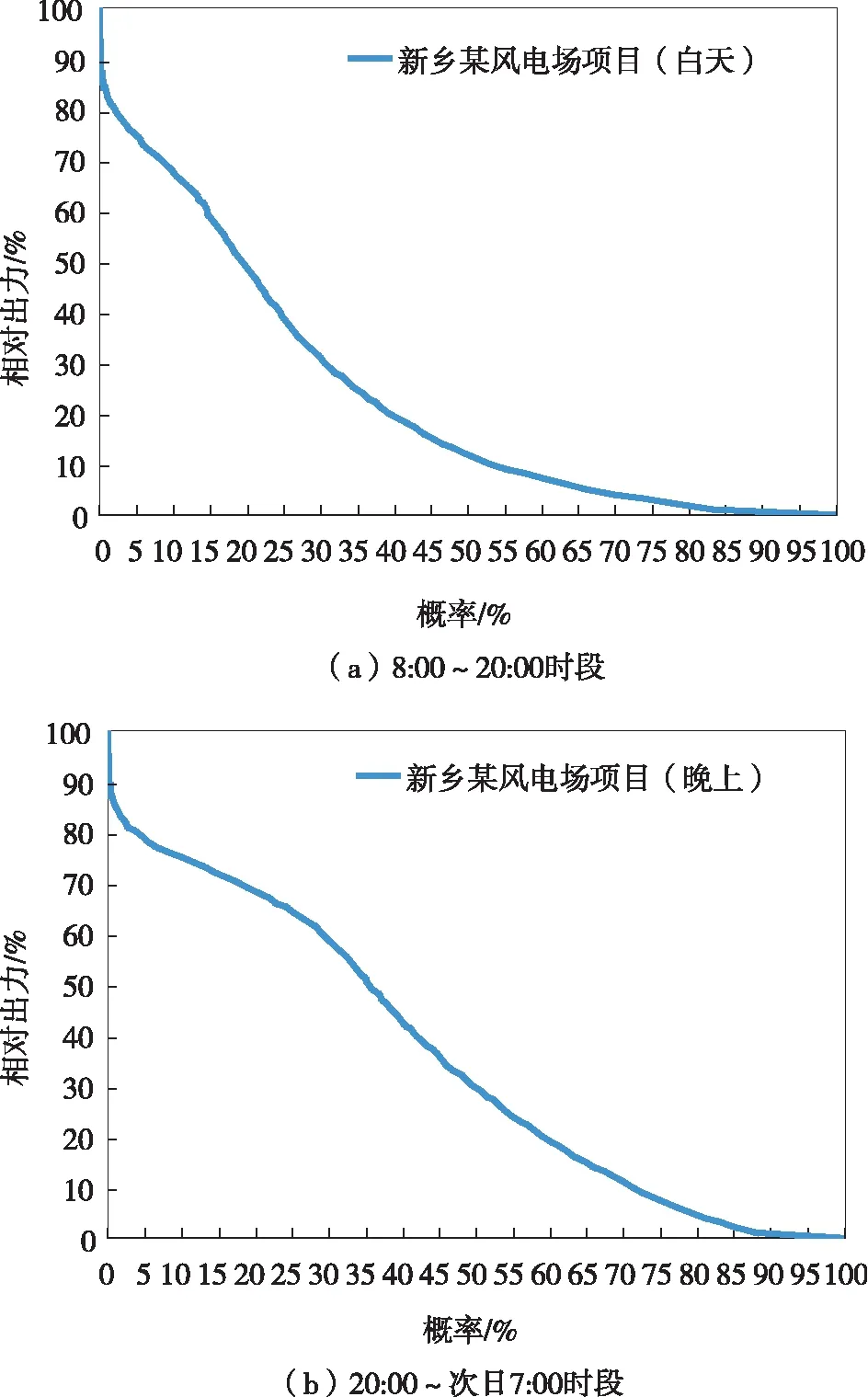
图5 新乡市典型风电场全年昼夜相对出力概率曲线

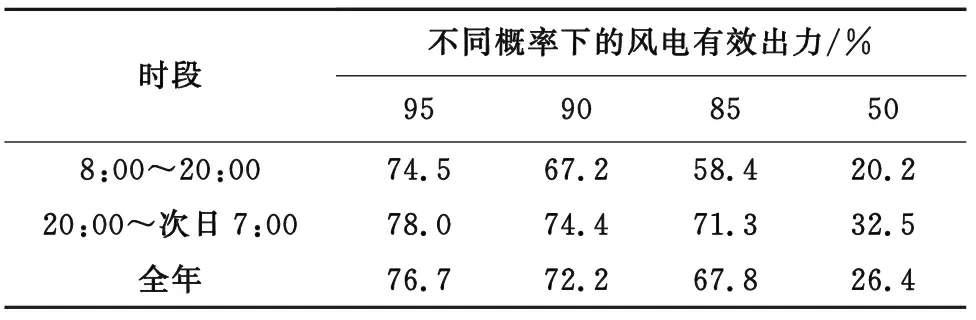
表5 新乡市典型风电场昼夜相对出力概率 %

图6为驻马店市典型风电场全年昼夜相对出力概率曲线，表6为驻马店市典型风电场昼夜相对出力概率。从图6及表6中可以看出驻马店市风资源昼夜的风电场有效出力差异较大，夜间95%概率下有效出力为72.2%，白天95%概率下有效出力为67.6%。随着概率值的减小，驻马店市风电场的有效出力明显下降，全年50%概率下有效出力为22.2%，白天有效出力仅为16.6%。

表6 驻马店市典型风电场昼夜相对出力概率 %

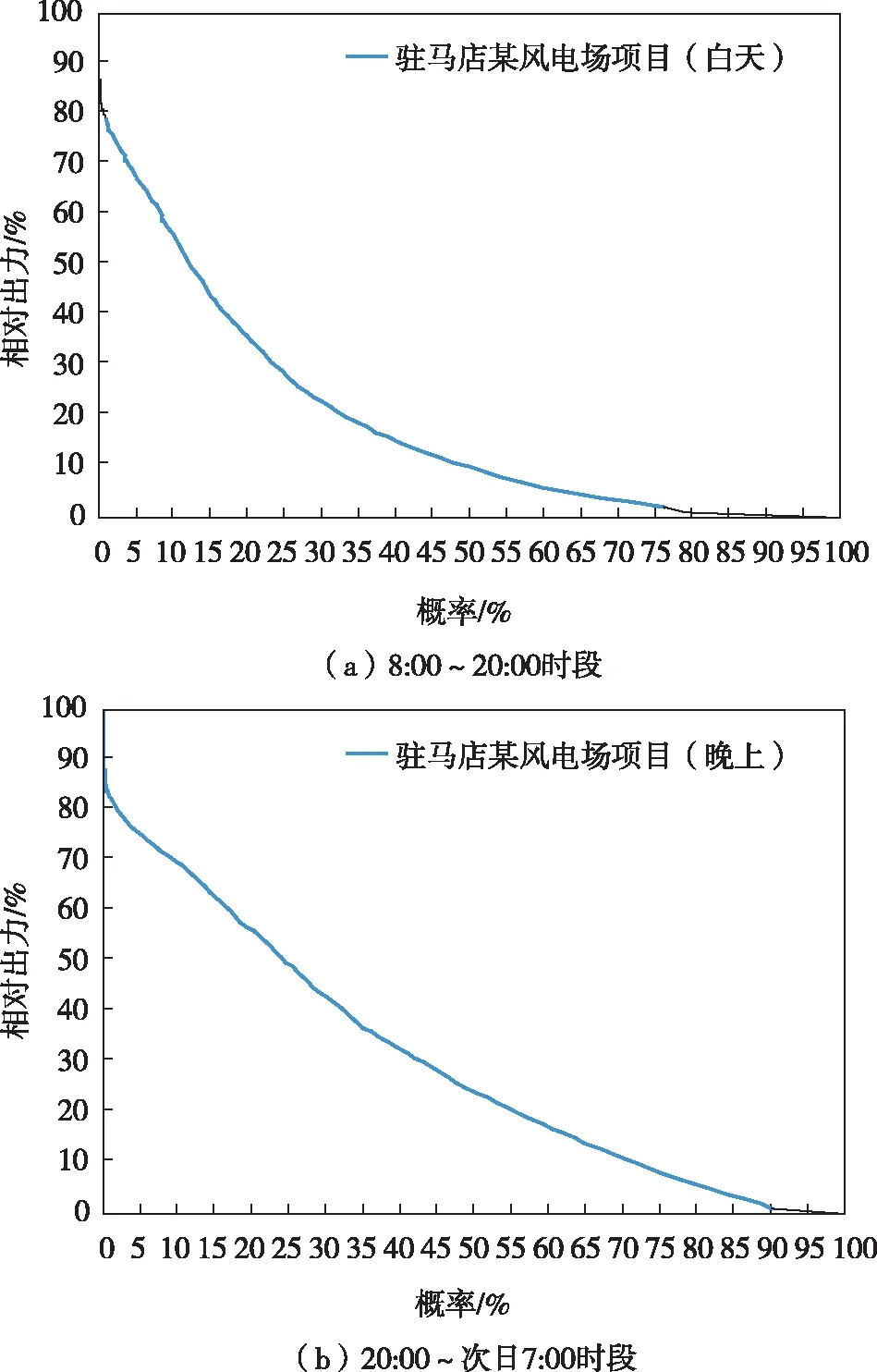
图6 驻马店市典型风电场全年昼夜相对出力概率曲线

图7为平顶山市典型风电场全年昼夜相对出力概率曲线，表7为平顶山市典型风电场昼夜相对出力概率。从图7及表7中可以看出平顶山市风资源昼夜的风电场有效出力差异较大，夜间95%概率下有效出力为75.2%，白天95%概率下有效出力为72.5%。随着概率值的减小，平顶山市风电场的有效出力明显下降，全年50%概率下有效出力为25.6%，白天有效出力仅为20.5%。

表7 平顶山市典型风电场昼夜相对出力概率 %

图5～图7表明河南省三区域风电场昼夜出力差异较大，表现为晚上出力明显大于白天出力，风电场有效出力与三个区域风资源分布存在明显关联。

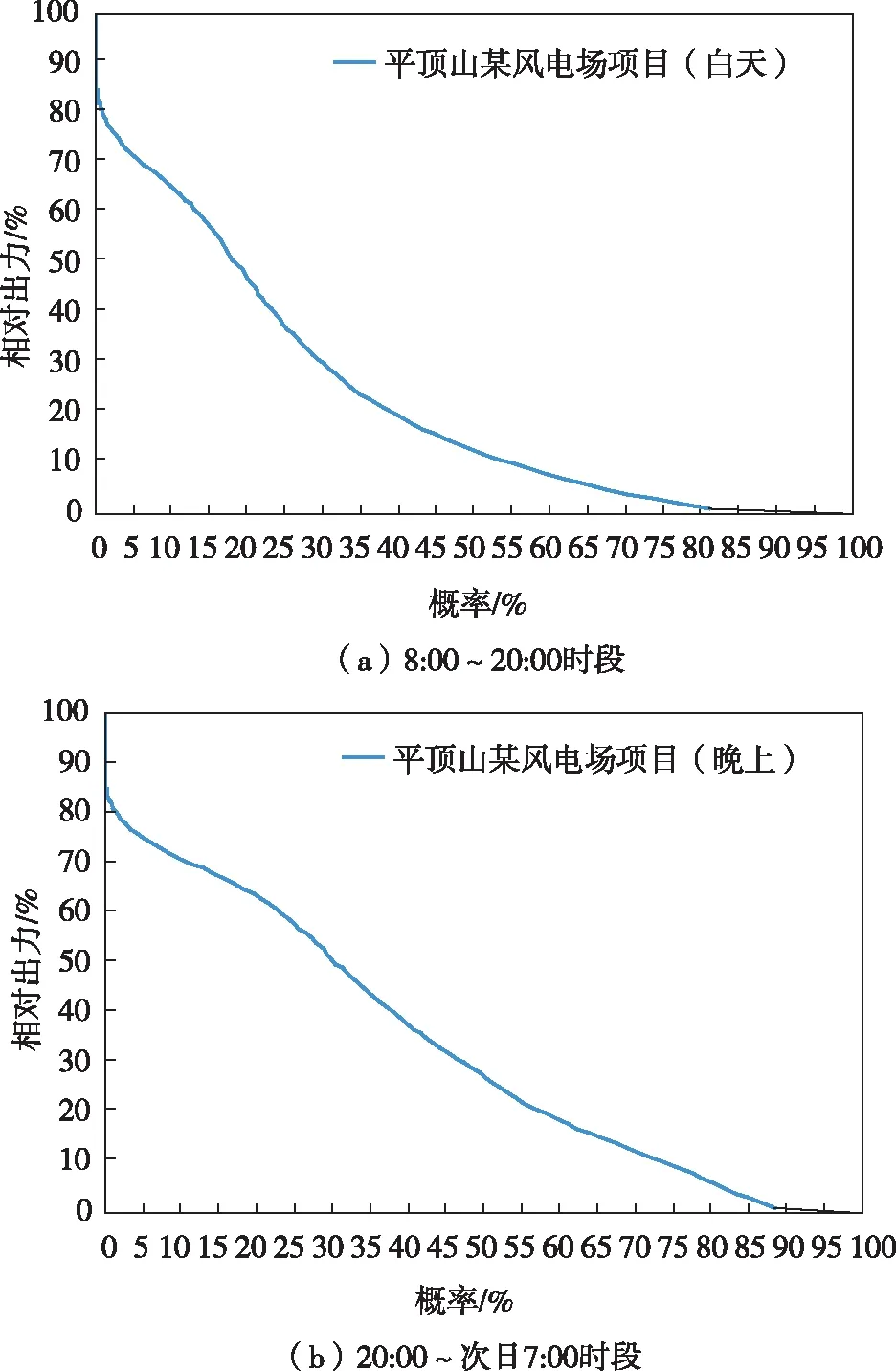
图7 平顶山市典型风电场全年昼夜相对出力概率曲线

4 结语

本文对考虑风电场不确定性方法的出力特性进行了研究，以测风塔实测数据长期代表性分析数据为基础，通过流体计算模型，提出基于风资源评估不确定分析方法的风电有效出力计算模型，并以河南省不同区域的三个规划风电场为研究对象进行分析。计算结果表明，该方法计算的风电场有效出力，能够降低因特定年份风速波动造成出力分析差异，为风电场接入系统技术参数选择、风电参与电力平衡计算等方面提供理论依据。