利用快中子散射截面定量评价砂泥岩储层含气饱和度的方法及应用
2022-04-26范继林梁国武王俊华
王 振,范继林,张 锋,3,梁国武,王俊华
(1.中海油田股份有限公司,河北 燕郊 065201; 2.中国石油大学(华东),山东 青岛 266580;3.深层油气重点实验室,山东 青岛 266580)
天然气是国家深地战略和国家绿色能源发展战略的重要基石。我国75%以上天然气来自复杂岩性和非常规油气藏,致密气成为天然气开发的一个主力勘探领域,主要包括陆相砂岩、海相碳酸盐岩等多种类型。致密气储层非均质性强,气、水关系复杂[1-2],气水层准确识别技术和有效储层预测技术尚不满足勘探开发要求。
目前,采用声波、电阻率、核磁等测井技术可以进行致密气储层含气识别与评价。张志虎等[3]利用密度和中子测井响应方程建立计算模型,在储层水电阻率不确定情况下定量求取含气饱和度。王大兴[4]利用声波测井资料进行致密砂岩储层含气评价,得到纵横波速度衰减和泊松比与储层孔隙度及含气饱和度呈近似负线性关系;尹帅等[5]研究在四川盆地须家河组以常规测井、元素俘获能谱测井(ECS)、核磁共振测井(NMR)及全波列测井资料进行评价,提高了预测精度。张筠等[6]开展核磁共振测井观测模式对比分析,以岩石弛豫特征和气水弛豫特征为基础,在四川盆地缝洞性碳酸盐岩储层进行气水识别。
作为核地球物理勘探中气体饱和度评估的重要方法,脉冲中子测井技术在含气饱和度评估中起着不可或缺的作用。Badruzzaman等[7]利用PNC及伽马计数比来确定密度和含气指示; Guo等[8]利用超长源距探测器定量评价孔隙度为3%~7%的泥砂岩储层的含气性;Bertoli[9]、Adrian[10]和Mamdouh[11]推出新型多探测器脉冲中子测井技术(MDPN),Zhou等[12]推出一种包含三个探测器的新型脉冲中子TMD-L测井技术,该脉冲中子测井仪通过长探测器伽马信息实现储层含气饱和度的评价。
基于甲烷、水和油对快中子散射能力的差异,本文提出一种利用快中子散射截面(FNXS)定量评价含气饱和度的方法。通过长探测器的非弹伽马射线表征FNXS,结合储层岩石体积物理模型,实现对储层含气饱和度的定量监测,建立含气储层饱和度的评价方法,为定量监测致密气藏中的天然气饱和度提供一种有效技术支持。
1 理论方法
快中子的探测效率极低,用次生伽马射线间接探测快中子是一种常用方法。脉冲中子测井技术中,D-T中子源可产生窄脉冲的快中子,向各个方向传播并与井眼和储层中的原子核相互作用。快中子进入地层后,在极短时间内与地层介质发生非弹性散射释放非弹伽马射线,同时发生弹性散射,中子逐渐慢化成为热中子,后被地层原子核俘获,释放俘获伽马射线。地层非弹性散射截面与密度呈正相关关系,即非弹性散射过程中产生的伽马射线越强,地层密度作用导致的伽马射线的衰减作用越强[12]。因此,将14 MeV的弹性散射截面作为快中子散射截面(FNXS)用以含气评价是一种合理的技术手段。
根据快中子散射理论[13],发生非弹性散射的快中子通量分布φf(r)如公式(1)所示:
(1)
式中,r为探测器源距,φ0为中子源强度。λs与FNXS分别为快中子散射自由程与快中子散射截面,满足互为倒数的关系。
利用中子伽马耦合场理论[14],非弹性散射伽马通量φin(R)如公式(2)所示:
(2)
式中,φin为非弹伽马射线通量,μm为质量衰减系数,ik为中子与每个元素一次碰撞中产生的伽马光子数,φf(r)为快中子通量分布,R为长探测器源距,Σin为地层的快中子非弹性散射截面,ρ为地层体积密度。
相对于地层快中子散射截面,快中子非弹性散射截面较小,可以将Σin视为定值。假定中子与每个元素一次碰撞中产生的伽马光子数ik不变,由公式(2)可知,由于不同岩性储层的属性参数(μm,ρ)存在差异,计算FNXS时需要考虑地层岩性参数的影响。因此,利用非弹性散射伽马通量表征FNXS满足以下公式:
FNXS=f(φin,Lith)
(3)
其中,Lith为地层岩性参数。公式(3)说明了地层FNXS的求取可以利用非弹伽马射线通量来表征,但会受到地层岩性的影响。因此,不同岩性地层需要建立不同的表征方法来满足FNXS计算的准确性。储层常见物质的快中子散射截面列于表1。

表1 储层常见物质的快中子散射截面
相比于储层骨架与孔隙油水的核物理参数,固体矿物质FNXS的大小与水和稠油的类似,气体的氢指数较低,热中子俘获截面、密度和FNXS存在较大差异。因此,含气储层中,利用FNXS可以将储层油气水三相流体转化为气液两相流体,为含气饱和度评价提供了一种新的方法。FNXS遵循岩石体积物理模型,在纯砂岩储层中,满足公式(4):
FNXS=FNXSmatrix(1-φ)+FNXSgasφSg+
FNXSoilφ(1-Sg)
(4)
由上式可以得到纯砂岩储层含气饱和度为:
(5)
在砂泥岩含气储层中,满足公式(6):
FNXS=FNXSmatrix(1-φ)(1-Vsh)+
FNXSsh(1-φ)Vsh+FNXSgasφSg+
FNXSoilφ(1-Sg)
(6)
则含泥质砂岩储层含气饱和度计算公式为:
Sg=(FNXS-FNXSmatrix(1-φ)(1-Vsh)+
FNXSsh(1-φ)Vsh-FNXSoilφ)/
(FNXSgasφ-FNXSoilφ)
(7)
式中,具有不同下标的FNXS表示不同储层组分的FNXS值(matrix为骨架,gas和g为甲烷,oil为油),φ为储层孔隙度,Vsh为泥质含量,S为饱和度。
2 蒙特卡罗数值模拟与FNXS表征
蒙特卡罗方法(MCNP)[15]可用于中子、光子、电子或耦合的中子、光子、电子传输输运过程,利用蒙特卡罗方法建立井筒-储层计算模型,模拟快中子输运过程,研究非弹性散射伽马计数与快中子散射截面关系,建立模拟数据与刻度井实验数据相结合的FNXS的表征方法,进而定量评价储层含气饱和度。
2.1 数值模型构建
MCNP数值计算模型示于图1。储层模型为高140 cm,直径140 cm的圆柱状套管井储层,井眼充满淡水,直径10.16 cm。水泥环由CaSiO3组成,密度为1.87 g/cm3,厚度2.54 cm;套管为不锈钢材质,厚度0.635 cm。储层孔隙度在0~30%范围内变化,含气饱和度为0、25%、50%、75%、100%。储层温度为323.15 K,压力为20 MPa,该地层温压条件下,甲烷、淡水和稠油的密度分别为0.12、1.00、0.95 g/cm3。

图1 仪器储层模型
三探测器脉冲中子测井仪用作储层含气饱和度监测器,源和每个探测器之间存在屏蔽装置。仪器外壳由17-4PH钢制成,厚度为0.5 cm。源为D-T脉冲中子源,产生高能中子(14 MeV)并向储层均匀发射。探测器材料为LaCl3晶体,三个探测器的源距分别为36、54、72 cm。三个探测器晶体的直径均为2.54 cm,长度分别为5.08、10.16、5.24 cm。
2.2 非弹性散射伽马计数响应
由于伽马射线计数数量级较大,选用伽马射线计数对数(lnN)进行研究。利用图1所示仪器地层模型,分别设置纯岩性砂岩、灰岩、白云岩和泥岩地层骨架,改变储层孔隙为0~30%,间隔5%,模拟纯含气与纯含水地层条件下,不同储层条件下的长源距探测器的伽马射线计数对数与FNXS的关系,形成快中子散射截面表征方法。图2展示了砂岩和泥岩(绿泥石)储层条件下,不同地层孔隙度、饱含气和饱含水储层FNXS关于长探测器lnN的变化关系。
由图2可知,同一岩性条件下,FNXS与lnN有着良好的线性负相关关系。利用长探测器伽马射线计数lnN可以实现FNXS的定量表征。砂泥岩条件下FNXS表征关系如下:

a——砂岩储层;b——泥岩储层
纯砂岩储层:FNXS=-3.34×lnN+30.04
(8)
纯泥岩储层: FNXS=-3.61×lnN+31.66
(9)
式中,FNXS为散射截面测量值,lnN为长探测器伽马计数对数。基于以上公式,通过测量的长探测器伽马信息,可以实时得到FNXS曲线,结合体积模型计算储层含气饱和度。
基于砂泥岩储层骨架物质组成,利用FNXS评价含气饱和度时需要进行地层岩性识别。在砂泥岩地层条件下,需要结合泥质含量对FNXS表征公式进行差值修正,满足实际地层岩性需求,以保证FNXS计算的准确性。
2.3 FNXS与含气饱和度响应关系
获取不同岩性地层下FNXS表征方法后,研究FNXS与含气饱和度的关系,实现储层含气饱和度的定量评价。利用图1所示仪器地层模型,在纯岩性地层条件下,将储层设置为充满油气的砂岩储层,改变孔隙度为0~30%,间隔为5%,同时改变含气饱和度为0~100%,间隔为25%。在不同的含气饱和条件下,模拟得到FNXS与储层孔隙度的变化示于图3。
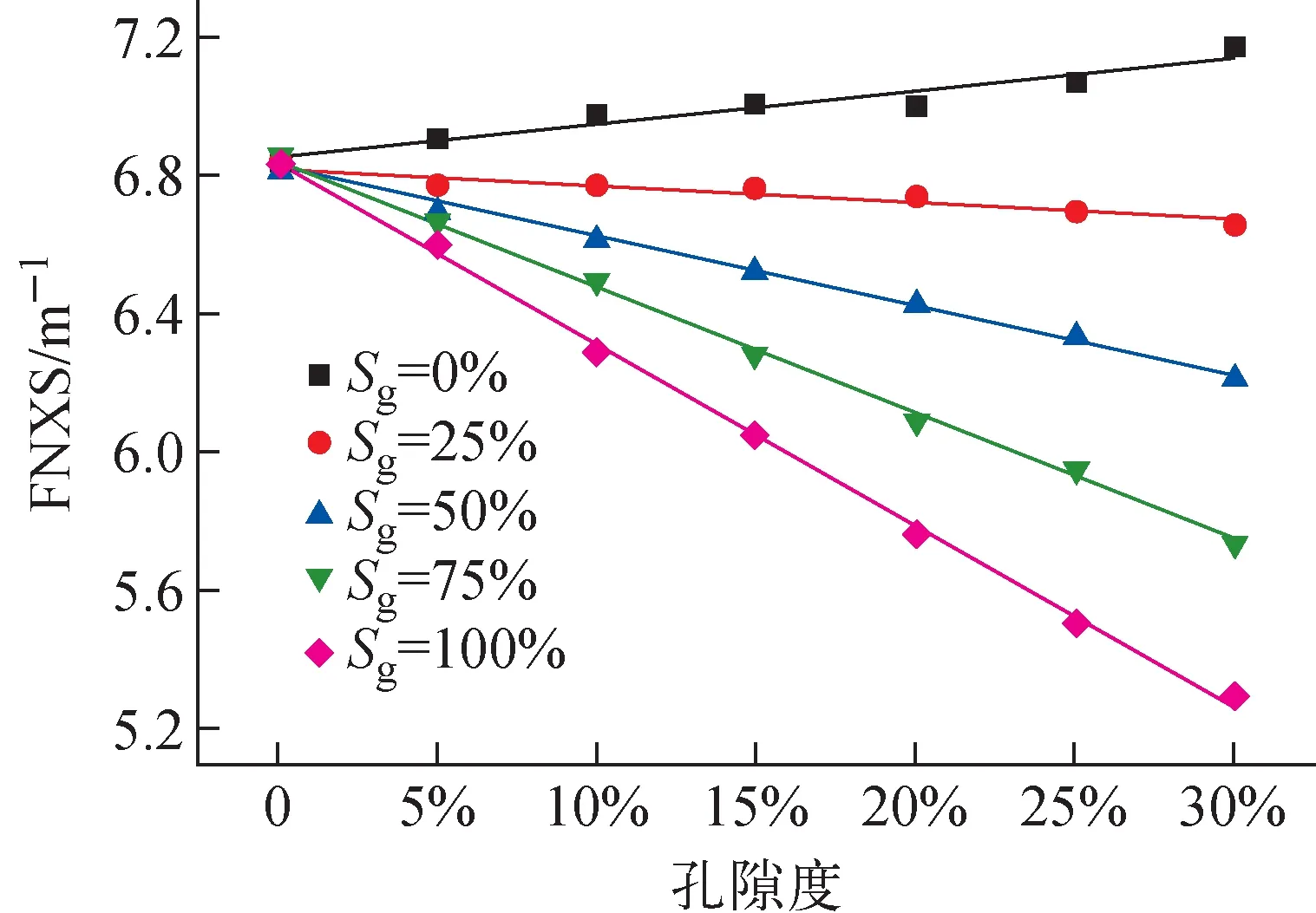
图3 FNXS关于储层孔隙度的变化
从不同含气饱和度条件下FNXS关于储层孔隙度的响应可以看出,在含气饱和度较低的情况下,FNXS随着孔隙度逐渐增加,而在含气饱和度较高的情况下,FNXS随着孔隙度逐渐减小。在油气混相储层中,当气体饱和度低时,油对快中子的慢化占主导地位;当气体饱和度高时,气对快中子的慢化占主导地位。不同含气饱和度条件下,FNXS关于孔隙度的变化关系差异明显,表明FNXS是一种良好的含气饱和度评价方法。
针对岩性较为复杂的储层,以含泥质砂岩为例,在储层泥质含量为0、10%、20%和30%条件下,改变孔隙度为0~30%,间隔为5%,同时改变含气饱和度为0~100%,间隔为25%。在不同的含气饱和条件下,含泥质砂岩储层FNXS与储层孔隙度的变化示于图4。

图4 泥质含量对FNXS测量的影响
由图4可以看出,与纯砂岩储层类似,在任意泥质含量储层条件下,含气饱和度较低时,FNXS随着孔隙度逐渐增加,含气饱和度较高时,FNXS随着孔隙度逐渐减小,但随着储层泥质含量增大,计算得到的FNXS相应升降低。储层FNXS主要受储层骨架、孔隙油水的影响,泥质的FNXS小于石英,相比于纯砂岩储层,尽管泥质与石英散射截面相差较小,但仍表现出由于泥质的存在导致地层整体FNXS降低的现象。因此,通过这一现象表明,在含泥质储层或复杂岩性储层,利用FNXS进行含气饱和度评价时,首先应对纯岩性的FNXS表征公式进行差值,获取适用于该含泥质储层或复杂岩性储层条件下的FNXS表征公式,是精准确定储层FNXS的前提。
2.4 含气饱和度计算精度模拟
利用FNXS进行储层含气饱和度求取过程中,对饱和度定量计算精度的研究十分重要。因此,基于砂岩地层储层的数值模拟模型,分别设置储层孔隙度为8%、10%、13%、16%、18%、21%、26%,同时对应的含气饱和度设置为73%、22%、36%、16%、91%、47%、62%。模拟获取长探测器计数对数lnN,通过公式(8)计算储层FNXS,结合岩石体积物理模型计算含气饱和度,并与含气饱和度设置值进行对比,获取上述条件下的含气饱和度计算精度,验证FNXS评价储层含气饱和度的有效性,结果列于表2。从表2可以看出,在任意孔隙度储层条件下,含气饱和度计算绝对误差控制在5%以内,表明利用FNXS进行储层含气饱和度的精度较高,验证了该方法的有效性。

表2 含气饱和度计算精度验证
3 现场实例验证
现场实例证明FNXS在致密储层条件下的含气饱和度评价的有效性。图5为X井1 760~1 800 m层段裸眼井资料与FNXS评价含气饱和度解释成果。该层段为致密砂泥岩储层,非储层段泥质含量较大,储层段以砂岩为主。储层整体孔隙度较低,约为10%~20%。除第一道深度道外,第2~8道均为裸眼井测井资料,第9道为长探测器伽马计数对数lnN测量值,第10道为FNXS曲线,第11道为含气饱和度。从X井计算的lnN曲线可以看出,含孔隙层段lnN为高值,FNXS曲线为低值,因此解释结果所示利用FNXS解释的含气饱和度约为50%,与裸眼井解释含水饱和度对应性良好。该层段已经射孔开采,产量较好,与解释结果吻合。

图5 X井FNXS评价含气饱和度解释成果
图6为Y井1 570~1 600 m层段利用FNXS进行含气饱和度评价的结果。该层段为致密砂泥岩储层,非储层段泥质含量较大,储层段以砂岩为主。储层整体孔隙度较低,1 580~1 584 m段孔隙度在10%以下,1 584~1 592 m段孔隙度接近20%。除第一道深度道外,第2~8道均为裸眼井测井资料,第9道为长探测器伽马计数对数lnN测量值,第10道为FNXS曲线,第11道为含气饱和度。从Y井lnN曲线可以看出,含孔隙层段lnN为高值,计算得到的FNXS曲线为低值,综合解释含孔隙储层段含气饱和度约50%,含气量较高,符合地区认识。

图6 Y井FNXS评价含气饱和度解释成果
4 结论
本文针对致密气储层的含气评价,基于甲烷、油和水对快中子散射能力的差异,将FNXS应用于致密砂岩储层的含气饱和度的定量监测,为致密气的定量评价提供了一种有效的方法。具体结论如下。
(1) 基于MCNP模拟手段,利用长探测器非弹伽马计数对数与FNXS呈负相关的特性,实现了纯岩性条件下FNXS的定量表征。
(2) 针对含泥质砂岩储层,利用差值实现了FNXS的表征,并利用含泥质岩石体积物理模型建立相应的含气饱和度计算模型,实现了含气饱和度的定量计算。
(3) 测井实例解释结果表明了该方法的解释结论与实际储层产量对应良好,验证了FNXS评价致密地层含气饱和度的有效性。
