复杂扰动下水下机器人的轨迹精确跟踪控制

陈浩华，赵红，王宁*,2，郭晨，鲁挺，王宁

1 大连海事大学 船舶电气工程学院，辽宁 大连 116026

2 哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001

0 引 言

水下机器人是一种可以按照预设指令或者操作者的意愿完成某项任务的智能水下航行器。其广泛用于民用和军事领域，如海上油气的勘探和开发，海洋环境的观测，鱼雷的排查等[1-3]。水下机器人的高精度轨迹跟踪控制是完成上述任务的前提，因而受到学者们的广泛关注[4]。然而，水下机器人是一个多自由度耦合、多变量的非线性系统，由于复杂的水下环境对其产生的干扰影响，如海浪、洋流和海洋生物的碰撞等，使得水下机器人的轨迹跟踪控制器的设计成为一个难点。控制器应该具有处理非线性和抗干扰的能力[5]。

滑模控制对系统中未建模部分不敏感，具备一定的抗干扰能力，因此被广泛用于水下机器人轨迹跟踪控制领域[6]。针对水下机器人的三维轨迹跟踪控制的问题，Qiao 等[7]提出了一种双闭环无抖振自适应滑模控制方法，解决了UUV 的三维目标轨迹跟踪控制问题。其设计了外环位置控制器和内环速度控制器，用饱和函数代替符号函数来克服外环的抖振。此外，设计了一个连续自适应项来代替传统滑模的不连续切换函数，并利用Lyapunov 稳定性理论证明了双环控制系统的全局渐近稳定。Rezazadegan 等[8]针对水下机器人三维轨迹跟踪控制的问题，提出了一种基于Lyapunov 直接法的自适应反步控制器。结果表明实际轨迹可以渐进收敛于期望轨迹，但是不能实现有限时间稳定。Guerrero 等[9]提出了一种自适应高阶滑模控制方法，在保留鲁棒控制的优点下，忽略扰动上界对系统的影响，并且将该算法应用到Leonard ROV 深度轨迹跟踪控制和偏航控制中，实验结果表明该控制策略可以有效抑制外界扰动和水动力学参数的不确定性。Qiao 等[10]针对时变外界干扰对水下机器人三维轨迹跟踪控制问题，提出了一种自适应非奇异积分终端滑模控制策略。消除传统滑模控制中的奇异问题，保证速度跟踪误差在有限时间内局部收敛到零，位置跟踪误差局部指数收敛到零。孙巧梅等[11]采用了反步滑模的控制策略，在外界干扰下，该控制策略得到了连续且平滑的控制输入，并且有效抑制了外界扰动。魏斯行等[12]在反步滑模控制的基础上，引入了一种生物启发神经动力学模型来解决平滑输出速度跳变的问题。仿真实验表明，对于缆控式水下机器人能够有效解决反步滑模造成的速度跳变。张伟等[13]引入了径向基函数神经网络和反步的方法来解决控制器运动参数在拐点处跳跃引起的跟踪冲击问题。同时，避免了单次反步控制中的奇异值问题。利用Lyapunov 稳定性理论分析了整个闭环控制系统的稳定性，但并不能实现对期望轨迹的精确跟踪。严浙平等[14]提出了一种双闭环终端滑模控制策略，将位置和姿态负反馈作为外环控制，并引入虚拟速度作为内环控制器的期望目标，采用终端滑模控制方法降低了抖振，使跟踪误差在有限时间内收敛，仿真实验表明该控制策略可以实现对空间轨迹的精确跟踪。但是设计过程较为复杂，计算量较大，不能广泛应用于水下机器人的轨迹跟踪控制。面对复杂的外界扰动，为进一步提高跟踪精度，Wang等[15-16]尝试使用观测器技术提高无人船的跟踪精度，及时补偿复杂的未知扰动，对姿态实现精准调节。

本文将针对水下机器人三维轨迹精确跟踪控制的问题，采用有限时间扰动观测器对外界复杂扰动进行观测，并结合非奇异终端滑模控制设计基于有限时间扰动观测器的非奇异终端滑模控制器（FDO-NTSMC）。其中所设计的FDO 可以精确观测外界时变干扰，降低扰动对系统的影响，提高系统的抗干扰能力，同时采用幂次趋近律降低NTSMC 产生的抖振。此外，将利用Lyapunov 函数及相关引理证明基于本文策略的水下机器人轨迹跟踪系统可以在有限时间内收敛。最后，通过仿真实验证明，在水下存在时变扰动及阶跃叠加扰动等复杂环境扰动时，本文FDO-NTSMC 策略不仅可以实现对水下机器人期望轨迹的精确跟踪，且比反步滑模控制策略（SMC）具有更好的控制性能。

1 预备知识和数学模型

1.1 预备知识

定理1[17]：考虑非线性系统

式 中：x=[x1,···,xn]T为 系 统n维 的 状 态 向 量；f(·)为 原点邻域上的非线性系统，且f(0) =0。若存在函数V(x,t)满足：

1）V(x,t)正 定，V˙(x,t)负定，则系统在原点处为渐进稳定；

2）V(x,t)正 定，V˙(x,t)半 负 定，除 原 点 之 外，V˙(x,t)不恒为零，则系统在原点处是渐进稳定；

3）V(x,t)正 定，V˙(x,t)半 负定，且当 ‖x‖→∞时，V(x,t)→∞，则系统在原点处是大范围渐进稳定。

引理1[18]：定义一正标量函数V(x)，若满足

式中， λ ＞0， 0 ＜θ ＜1。则系统式(1) 有限时间稳定，且其有限时间T满足如下不等式

式中，V(x(t0)) 为V(x(t))的初始值。

引理2[19]：考虑以下系统

式 中： βi＞0(i=0,1,···,n)，L＞0，为 常 数；n为 系统阶数。如果系统满足上述条件，则其有限时间稳定。

1.2 数学模型

水下机器人的运动状态需要依靠坐标系进行描述，如图1 所示，分别以大地为坐标原点建立惯性坐标系E-ξηζ，以水下机器人的重心为坐标原点建立附体坐标系O-xoyozo。

图1 坐标系Fig. 1 Coordinate system

根据Fossen 等[20]提出的潜水器动力学建模方法得到水下机器人六自由度数学模型。由于水下机器人在运动的过程中其横滚角变化较小，因此可以忽略其对水下机器人的影响，得到水下机器人五自由度数学模型。

式中：惯性坐标系下， η=[x,y,z,θ,ψ]T，x为水下机器人纵向位移，y为横向位移，z为垂向位移， θ为俯仰角， ψ为偏航角；附体坐标系下， υ=[u,v,w,q,r]T，u为纵向速度，v为横向速度，w为垂向速度，q为俯仰 角 速 度，r为 偏 航 角 速 度； τ=[τ1,τ2,τ3,τ4,τ5]T，τ1为 纵向控制力， τ2为 横向控制力， τ3为垂向控制力，τ4为俯仰角控制力矩，τ5为偏航角控制力矩；τδ=MJ-1(η)δ(t)为在对应方向上受到的外界干扰，其中，δ(t)=[δ1,δ2,δ3,δ4,δ5]T；M为质量与附加质量矩阵，且有M=MT＞0；C(υ)为科氏向心力矩阵，且有C(υ)=-CT(υ)；D(υ)为阻尼矩阵；g(η)为恢复力矩阵；J(η)为惯性坐标系与附体坐标系转换矩阵，具体描述如下：

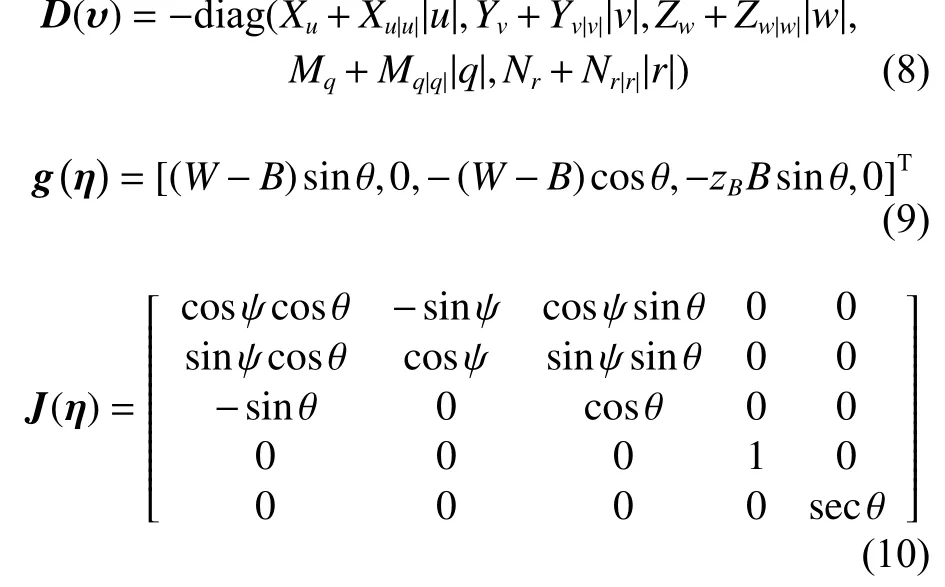
式中：m为水下机器人的质量；Iy，Iz为转动惯量；Xu˙，Yv˙，Zw˙，Mq˙，Nr˙分 别 为 横 向、纵 向、垂 向、俯 仰角和航向角5 个自由度的水动力导数；Xu，Yv，Zw，Mq，Nr分别为横向、纵向、垂向、俯仰角和航向角5 个 自 由 度 的 一 阶 阻 尼 系 数；Xu|u|，Yv|v|，Zw|w|，Mq|q|，Nr|r|分别为横向、纵向、垂向、俯仰角和航向角5 个自由度的二阶阻尼系数；W和B分别为水下机器人所受到的重力和浮力；zB为附体坐标系下浮心在z轴坐标，即浮心高度。

控制目标：依据水下机器人的数学模型式(5)建立期望轨迹下的数学模型，构造跟踪误差方程，并根据此方程设计控制器 τ。当存在外界多种复杂时变扰动时，基于该控制策略下的水下机器人轨迹跟踪系统不仅可以在有限时间内实现对期望轨迹的精确跟踪，而且可以得到一条较为光滑的控制输入曲线。

2 FDO-NTSMC 控制器设计

2.1 问题描述

期望轨迹下的数学模型，描述如下：

式中：ηd=[xd,yd,zd,θd,ψd]T为期望位置和航向角；

υd=[ud,vd,wd,qd,rd]T为期望速度和角速度；τd=[τd1,τd2,τd3,τd4,τd5]T为期望轨迹对应的控制输入。

为了便于说明控制器的设计过程，定义以下状态变量：

式中， ω =[ω1,ω2,ω3,ω4,ω5]T为实际期望位置和航向角， ωd=[ωd1,ωd2,ωd3,ωd4,ωd5]T为实际速度和角速度，其中 ω1～ω5分别为水下机器人在惯性坐标系下的纵向、横向、垂向速度与俯仰角及航向角角速度的实际值， ωd1～ ωd5为上述5 个变量对应的期望值。

结合状态变量方程，将式(5)改写为

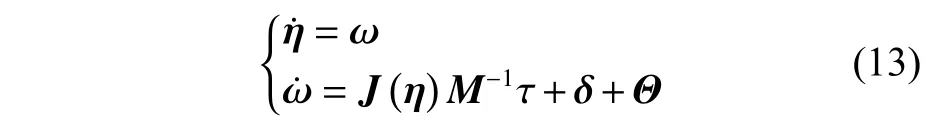
其中，

相同的，式(11)可改写为

其中，

结合式(13) 和式(14)，得到系统跟踪误差方程：

其中：

2.2 控制器设计

在外界存在多维度干扰的情况下，为使水下机器人实现对三维期望轨迹的精确跟踪，基于跟踪误差方程(15)设计了FDO-NTSMC 控制器。

第1 步：针对外界多维度时变扰动，设计有限时间扰动观测器进行补偿。

假设1：式(15)中外界扰动 δ满足

式中，Lδ＞0有界且为常数。

针对跟踪误差系统方程中的扰动，有限时间扰动观测器设计如下：

其中，

式中：z0为 速度误差的估计值，z1为外界扰动的观测值，z2为外界扰动一阶导数的估计值，其中zi∈R5x1(i=0,1,2) ；βi＞0(i=0,1,2)为 增 益 系 数，L=diag(l1,l2,l3,l4,l5)为有限时间扰动观测器参数；sigθ(x)=|x|θsign(x)。

第2 步：设计非奇异终端滑模面s：

式 中：k＞0， 为 常 数；p，q为 正 奇 数， 且 有q/p∈(1,2)。

对式(19)求导，并结合式(15)，得

式中，diag(·)表示对角矩阵。为保证求导后维度正确，将ω改写为diag(ω。

根据设计的滑模面式(20)，控制器可设计为

其中，等效控制项为

鲁棒控制项为

式中：选取幂次趋近律s˙=κ|s|αsign(s)，可以保证在有限时间内到达滑动面，其中，κ=diag(κ1,κ2,κ3,κ4,κ5)，κi＞0(i=1,2,3,4,5) 为 常 对 角 矩 阵； α为 常数，且0＜α＜1； sign(s)=[sign(s1),sign(s2),sign(s3),sign(s4),sign(s5)]T，sign(·)表示符号函数，并且有以下性质：

2.3 系统稳定性分析

定理2：针对假设1 下的多维度时变复杂扰动，设计的有限时间扰动观测器可以实现对扰动的观测，补偿扰动对系统的影响，提高鲁棒性。

证明：

对于所设计的有限时间扰动观测器式(17)，定义观测误差方程，即

对上式等号两端求导， 结合式(17)和式(18)，得

式(26)还可以写成

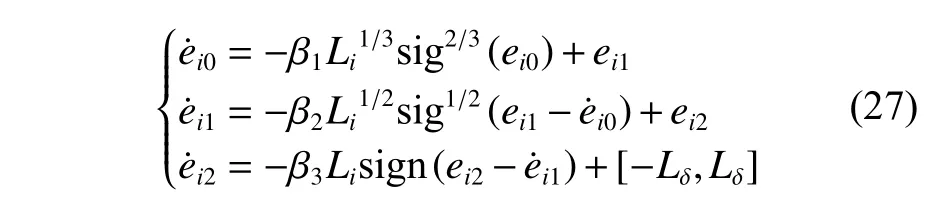
由引理2 可知，式(27)有限时间稳定，即所设计的有限时间扰动观测器可以在有限时间内对扰动进行观测。并且在有限时间内有

因此可以得到观测误差z1-δ ≡0。证毕。

定理3：考虑外界多维度时变干扰 δ影响下的水下机器人数学模型，在控制律 τ的作用下，系统可以在有限时间内驱动状态变量到达滑动面s(t)=0，使位姿跟踪误差变量在有限时间内收敛于零，即实际位姿向量 η和速度向量 υ跟踪上参考位姿向量 ηd和 期望速度向量 υd。

证明：

将式(21)代入式(20)，整理后得

结合定理1，上式可以写为

定义Lyapunov 函数：

对其求导，并将式(30)代入，得

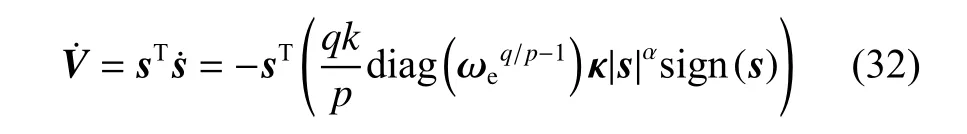
令

当ωei≠0(i=1,2,3,4,5)时 ， 由 于q/p-1 ＞0，k＞0， κ ＞0 且q，p为正奇数，可以得到Q为正定矩阵，即 λmin(Q)≥0。那么，式(32)可以改写为：

根据定理1，可知该系统渐进稳定。下面进一步证明系统有限时间稳定。令

结合式(31)与式(34)～式(35)，整理后得

由于0 ＜α ＜1， 得1 /2 ＜(α+1)/2 ＜1，根据引理1可知，系统有限时间收敛。

当ωei≠0(i=1,2,3,4,5)时，根据式(21)～式（23)和式(15)，有

由上式可得，当si＞0 时， ω˙ei＜0 ， ωei快速减小；当si＜0 时， ω˙ei＞0 ， ωei快 速 增大。因此，当ωei=0时，在有限时间内有s(t)=0。 即跟踪误差 ηe和速度跟踪误差 ωe在有限时间内到达滑模面[21]。

根据上述证明可知，本文所设计的FDONTSMC 可以使水下机器人在有限时间实现三维轨迹的精确跟踪，系统跟踪误差可以在有限时间内被镇定到零。

3 仿真实验研究

为了证明本文所设计控制器的优越性和有效性，借鉴文献[22]中水下机器人的动力学模型和水动力参数，在相同的初始条件下，与反步滑模BSMC 和非奇异终端滑模NTSMC 进行对比仿真实验。同时，为验证基于本文方法的暂态和稳态精度，采用绝对误差积分准则（integral absolute error，IAE）和时间乘绝对误差积分准则（integral time absolute error，ITAE）指标进行衡量[23-24]。表达式为：

式中，e(·)表示位姿跟踪误差，采用绝对误差积分准则的计算结果为fIAE，采用时间乘绝对误差积分准则的计算结果为fITAE。

其中，产生期望轨迹的控制输入为：τd=[50,30cos(0.1πt)2,20cos(0.1πt)2,-12cos(0.1πt)2，12cos(0.1πt)2]T。 选取水下机器人的初始位姿η(0)=[15,7.2,2.7,0,0]T，初始速度及角速度υ (0)=[0,0,0,0,0]T。假设外界多维度时变干扰为：δ=[0.3cos(0.2πt-π/3),0.4cos(0.4πt-π/4) ，0.6cos(0.6πt-π/6), 0.2cos(0.2πt-π/2), 0.3cos(0.4πt-π/3)]T，阶跃扰动为：δ2=[5,5,5,5,5]T。FDO-NTSMC 控制器关键参数取q=7，p=5，k=2 ， α=0.7， κ=diag(3.6,3.6,3.6,3.6,3.6)； 有 限 时 间 扰 动 观 测 器 参 数 取 β1=2.2，β2=2.6， β3=0.8，L=diag(30,30,30,30,30)。

1） 仿真实验工况1：水下存在如上扰动 δ时，基于本文算法与NTSMC 和BSMC 算法分别进行了水下机器人三维轨迹跟踪的仿真实验，仿真结果如图2～图8 所示。

由图2～图4 可以看出，水下存在扰动 δ时，虽然NTSMC 和BSMC 控制策略可令水下机器人完成对期望轨迹的跟踪，但却无法实现精确跟踪，即存在波动的跟踪误差，而FDO-NTSMC 控制策略可令轨迹跟踪误差为零。图5 所示的控制输入曲线表明，与BSMC 策略相比，FDO-NTSMC 具有更为平滑的控制输入，更利于执行器工作，且其中的有限时间扰动观测器可以对外界复杂扰动实现精确观测（图8），故可以及时补偿外界扰动对系统的干扰，提高系统的抗干扰能力。由图6～图7所示的速度与速度误差曲线可见，本文设计的控制器相较于NTSMC 更有优势。

图2 工况1 的跟踪轨迹Fig. 2 The tracking trajectory for condition 1

图3 工况1 的位姿状态曲线Fig. 3 Position states for condition 1

图4 工况1 的位姿跟踪误差曲线Fig. 4 Position errors for condition 1

图5 工况1 的控制输入曲线Fig. 5 Control input for condition 1

图6 工况1 的速度状态曲线Fig. 6 Speed states for condition 1

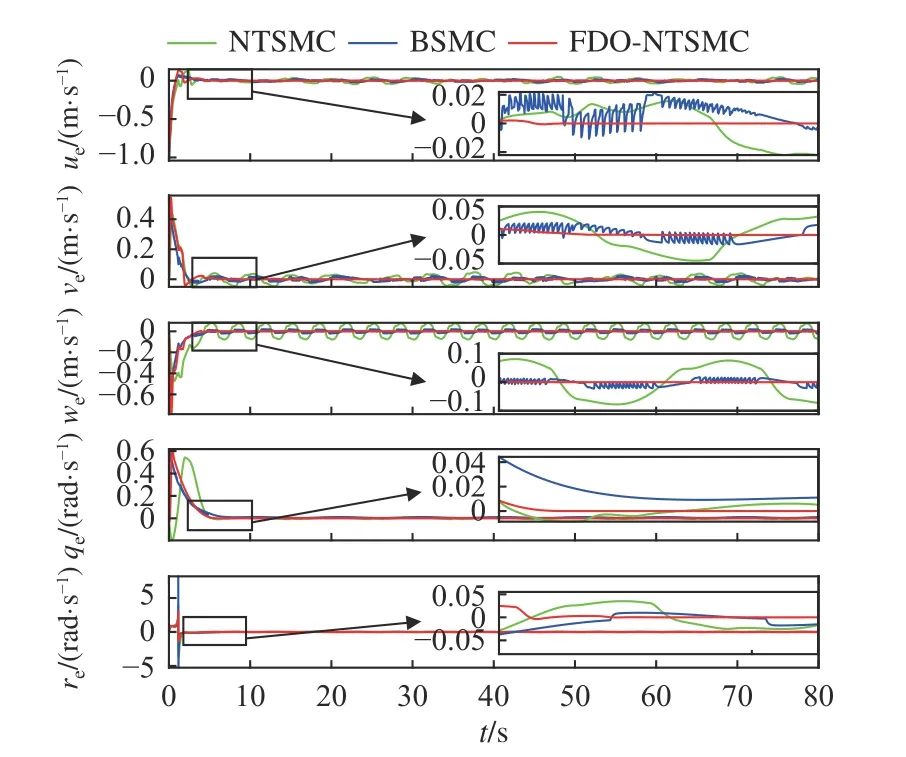
图7 工况1 的速度跟踪误差曲线Fig. 7 Velocity errors for condition 1

图8 工况1 的水下扰动及其观测曲线Fig. 8 Disturbance and observed values for condition 1

2） 仿真实验工况2：水下环境中除了存在如上扰动δ，于30～40 s 处再叠加一阶跃扰动。在相同的初始条件下，得到FDO-NTSMC，NTSMC 和BSMC 仿真实验结果，如图9～图15 所示。

图9 工况2 的跟踪轨迹Fig. 9 The tracking trajectory for condition 2

图10 工况2 的位姿状态曲线Fig. 10 Position states for condition 2

通过图9 可以看出，30～40 s 处叠加阶跃扰动后，NTSMC 与BSMC 控制策略均无法实现对参考轨迹的跟踪，而本文提出的FDO-NTSMC 仍能实现对参考轨迹的精确跟踪，这一点通过图11 位姿跟踪误差结果也得到了验证。通过图15 可以看出，在叠加阶跃扰动后，本文所设计的有限时间扰动观测器依然可以对叠加后的扰动实现精确的观测，以及时补偿阶跃扰动对系统的影响，故提高了轨迹跟踪系统的鲁棒性。

图11 工况2 的位姿跟踪误差曲线Fig. 11 Position errors for condition 2

图12 工况2 的控制输入曲线Fig. 12 Control input for condition 2

图13 工况2 的速度状态曲线Fig. 13 Speed states for condition 2

图14 工况2 的速度跟踪误差曲线Fig. 14 Velocity errors for condition 2

图15 工况2 的水下扰动及其观测曲线Fig. 15 Disturbance and observed values for condition 2

3） 仿真实验工况3：在仿真实验工况1 下控制输入曲线的结果中，由于初始时刻水下机器人轨迹跟踪误差较大且存在多维度时变干扰，故而需要较大的动力，导致控制输入曲线存在较大的阶跃突变。但这在实际的工程应用中不存在，执行器需要在安全范围内工作，因此对3 种方法下的控制输入进行合理限幅。得到以下实验结果，如图16～图22 所示。

图16 工况3 的跟踪轨迹Fig. 16 The tracking trajectory for condition 3

图17 工况3 的位姿状态曲线Fig. 17 Position states for condition 3

图18 工况3 的位姿跟踪误差曲线Fig. 18 Position errors for condition 3

图19 工况3 的控制输入曲线Fig. 19 Control input for condition 3

图20 工况3 的速度状态曲线Fig. 20 Speed states for condition 3

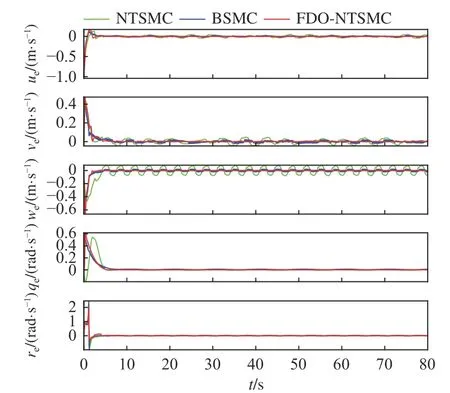
图21 工况3 的速度跟踪误差曲线Fig. 21 Velocity errors for condition 3

图22 工况3 的水下扰动及其观测曲线Fig. 22 Disturbance and observed values for condition 3

通过图19 可以看出在控制器限幅后，BSMC的控制输入曲线出现了较强的抖振，而本文所设计的控制方法与限幅前相同，为较为光滑的控制输入曲线。以上为基于3 种控制方法的水下机器人三维轨迹跟踪控制研究的定性分析。为了更加直观地分析本文控制方法的优势。以下采用绝对误差积分准则IAE 和时间乘绝对误差积分准则ITAE 指标对上述3 种工况的控制性能进行暂态和稳态精度的定量分析。数据结果如表1～表3所示。

表1 三种方法的性能比较Table 1 Performance comparison of three methods

表2 阶跃扰动下3 种方法性能比较Table 2 Performance comparison of three methods under step perturbation

表3 执行器限幅下3 种方法性能比较Table 3 Performance comparison of three methods under the condition of limiting amplitude of control input

通过对比3 种工况下的IAE 指标，BSMC 与FDO-NTSMC 均小于NTSMC，且本文提出的基于FDO-NTSMC 的控制方法略小于BSMC，具有较高的暂态精度。对比3 种工况下的ITAE 指标，结果表明FDO-NTSMC 的ITAE 性能指标远小于BSMC 和NTSMC，故而基于FDO-NTSMC 的控制方法可令水下机器人对期望三维参考轨迹实现高精度跟踪，即通过量化的方式进一步验证了本文控制策略的优越性，基于FDO-NTSMC 的控制方法具有较高的稳态精度[25]。

4 结 论

本文针对复杂多维度时变扰动下水下机器人三维轨迹精确跟踪问题，提出了基于有限时间扰动观测器的非奇异终端滑模FDO-NTSMC 控制策略。通过设计有限时间扰动观测器解决水下复杂时变扰动对水下机器人轨迹跟踪系统的干扰问题，并完成了理论验证。同时，为了降低非奇异终端滑模NTSMC 所产生的抖振，采用幂次趋近律代替以往文献[26]中使用的等速趋近律，保证了跟踪误差可以在有限时间内被镇定到零。最后，在相同的仿真实验条件下，与非奇异终端滑模NTSMC 和反步滑模BSMC 控制策略进行了对比实验研究，并使用IAE 和ITAE 性能指标对跟踪精度进行量化，仿真结果验证了本文所提策略的有效性与优越性。