广义岭估计在矩阵病态问题中的应用
2022-04-26王其腾吴风华
王其腾,吴风华
(华北理工大学 矿业工程学院,河北 唐山 063210)
测量数据的误差处理是测量工作中最重要的环节之一,其对测量精度产生直接影响[1]。最小二乘(LS)估计在测量数据呈现线性回归时,可以有效地对误差进行消除[2]。但是若测量数据不是线性回归,甚至呈现病态(即列向量之间存在严重的复共线型)时,LS估计处理的效果就很差[2-4]。故当设计矩阵呈现病态时,需要设法消除其对最终测量精度的影响。有偏估计的提出就是为了消除矩阵病态影响,目前常用的有偏估计方法有岭估计(Ridge Estimation)、广义岭估计(Generalized Ridge Estimate)、主成分估计(Principal Component Estimate)[5]。分别运用上述4种估计方法,利用MATLAB结合实际数据进行运算,验证了广义岭估计在处理设计矩阵病态问题中有较另外2种具有偏估计更好的处理能力。
1设计矩阵病态及其判定
病态矩阵在测量数据处理中极其常见,因为在测量过程中,测量数据基本呈现非线性回归,这样就导致了设计矩阵各列向量之间可能存在严重的复共线性,称之为病态矩阵[6]。当矩阵呈现病态时,其所对应的逆矩阵以及以该矩阵为系数的方程组的值都会因其微小的波动而产生较大的改变,对最终结果的运算带来很大难度。
复共线性的诊断与度量是病态矩阵判断的主要依据,目前比较常用的诊断方法有条件数法、特征分析法和方差膨胀因子法[7]。选择条件数法作为诊断依据。
方N的条件数定义为:
(1)
式(1)中:λmax,λmin分别为N的最大及最小特征值。
根据上式,可很直观地对N的特征值的离散程度进行判断,从而进一步对复共线性是否存在以及矩阵病态程度进行判断,最终对诊断模型病态性及病态程度进行判定。从以往大量的实际应用生产中进行经验总结,可以大致地对条件数P进行如下判定:
(1)若0 (2)若100≤P≤1 000,则可以确定其存在较高程度的复共线性; (3)若P>1 000,则其复共线性程度最强,病态最严重。 现有线性平差模型: (2) 式(2)中:设n为观测值个数,N=BTB满秩,同时t=rank(N),那么有X的最小二乘解[4] (3) 具有唯一性,并且其为最优的线性无偏估计解。但是在实际生产问题中,式(2)中N的行列式可能会很小,即det(N)≈0,数学中称这种设计矩阵为病态矩阵,其所对应的法方程为病态方程,其解非常不稳定[8]。岭估计、广义岭估计以及主成分估计的提出均是为了解决当设计矩阵病态时,如何获得更优解的问题。 岭估计是由最小二乘估计改进的一种有偏估计,其中参数X的岭估计为[9]: (4) 式(4)中:k>0为任意常数,称其为岭参数或偏参数。若k=0啊,则式(3)与式(4)相同。岭估计相较于最小二乘估计最重要的改善是通过加入岭参数K的概念来打破系数阵B的病态性,所以在进行岭估计运算时,岭参数K的确定就显得尤其重要。许多统计学家提出了不同的确定岭参数K的办法,但是却没有一种办法得到大家的公认,目前岭迹法和双h法是比较常用的方法[10]。该项研究选择双h法进行岭参数K的确定,公式如下: (5) 若将典则形式下的系数阵对角线上加上不同的参数k,将转换为广义岭估计。故参数X的广义岭估计为: (6) 上式中,G为对应与N=BTB的特征根λ的标准正交化特征向量有: GT(BTB)G=Λ=diag(λ1,…λt),K=diag(k,…kt) (7) 式(7)中:k,…kt为t个岭参数或称广义岭参数。 主成分估计是将病态矩阵的一些趋近于0的特征根所对应的成分从线性模型中剔除,对剩余的成分仍采用LS估计,最后根据关系X=GY确定X的估计。那么参数X的主成分估计为: (8) 当r=t时,式(8)与式(2)相同。 图1所示为数据处理设计方案。 图1 数据处理设计方案 在数据选择过程中,因普通且未经任何处理的数据并不能保证其具有病态效果,故选择文献[2]中所设计的方程系数阵,满足其病态要求,同时因其为病态的方程系数矩阵,与实际生产过程中所产生的病态数据所对应的系数阵基本相同,故其能代表普遍数据,满足实验要求。加入随机误差后的设计矩阵和观测向量为[3,11]: (9) (9) 根据算例数据利用MATLAB编程,计算N=BTB的条件数为P=20 836.718 116 457 6,存在严重病态。遂利用上述3种有偏估计的程序分别进行运算。因选择的数据为严重病态的数据,但为了展示效果,同时也运用最小二乘估计进行运算,运算结果只作为参考。 通过进行最小二乘估计以及上述3种有偏估计对算例数据进行运算,得到估计值如表1所示。 表1 不同估计方法估计结果 在实际工作中,无法通过参数估值来对估计方法消除矩阵病态的程度进行判定,所以对上述4种参数估值进行求均方误差(MSE)和2-范数(F)运算,最后通过MSE及F对效果进行判定,下面对2-范数的定义进行简单说明。 矩阵的2-范数,就是矩阵的转置共轭矩阵与矩阵的积的最大特征根的平方根值,是指空间上2个向量矩阵的直线距离[12]。表2所示为不同估计方法MSE、2-范数结果。 分别将参数估计值、均方误差及2-范数结果在图中进行对比,如图2、图3所示。 图2 4种估计方法估值对比 图3 4种估计方法MSE、2-范数对比 由于所选设计矩阵为严重病态,而最小二乘矩阵在处理矩阵病态问题中并不具备优势,故该研究中最小二乘估计仅作为参考,不参与最终的结果分析。 通过上述步骤可以发现,不同估计方法所得结果存在很大的差异,甚至在运用主成分估计进行运算时,x_3参数的符号也发生了变化,另外两种有偏估计相对于最小二乘估计虽然并没有发生符号的改变,但是其参数估计值也存在或大或小的差异。表明3种估计方法对矩阵病态的消除能力不尽相同。 在图3中,通过对3种有偏估计以及最小二乘估计的均方误差(MSE)和2-范数(F)进行分析,可以明显地发现。在均方误差(MSE)的对比中,岭估计与最小二乘估计的消除病态能力大致相同,而主成分估计和广义岭估计有较大的消除能力,尤其是广义岭估计的消除效果更为明显;在2-范数(F)的对比分析中,可以发现最小二乘估计、主成分估计、岭估计与广义岭估计的消除病态能力逐步升高。 故通过选择严重病态的算例数据,分别运用主成分估计(PCE)、岭估计(RE)与广义岭估计(GRE)对算例中数据的处理,通过MSE及F-2直观地分析出广义岭估计的消除矩阵病态的能力强于另外2种有偏估计方法。 (1)广义岭估计对典则形式下的系数阵对角线上加上了不同的广义零参数k,这就导致广义岭估计的消除能力强于只添加岭参数k的岭估计,而主成分估计可能是因其去除了数据中非主要成分的影响,导致消除能力下降。 (2)当数据呈现严重病态时,广义岭估计消除矩阵病态的能力是最强的,这就为处理矩阵病态数据时提供了更好的解决办法。2原理与方案设计
2.1 原理基础
2.2 设计方案
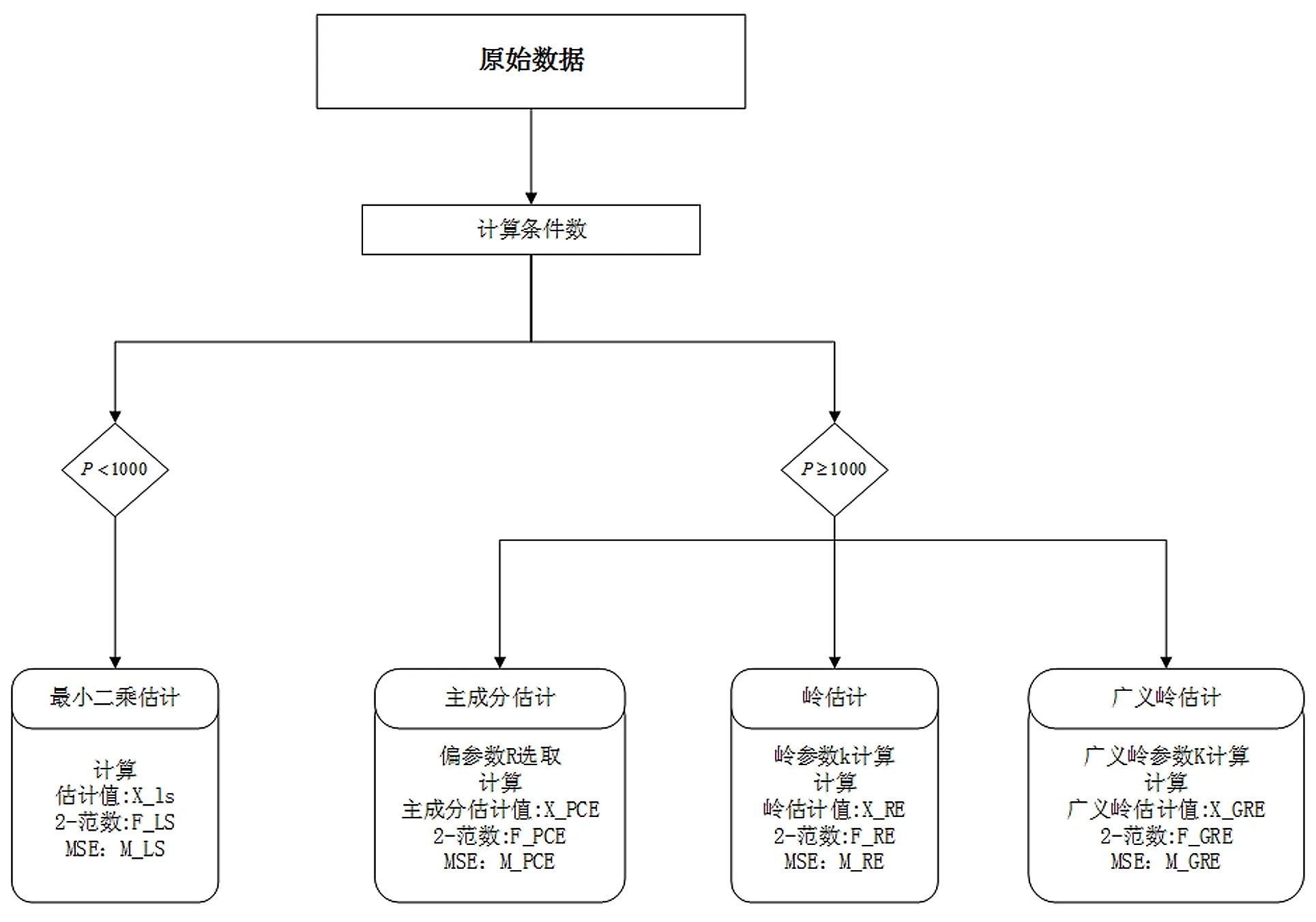
3算例计算
3.1 算例
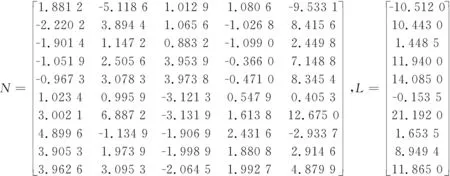


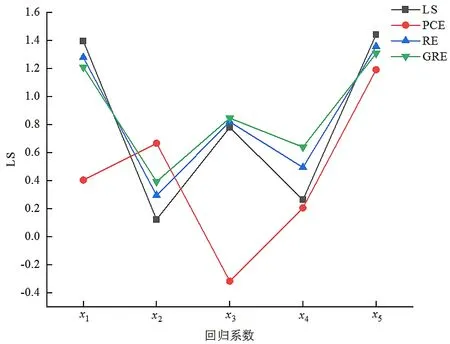
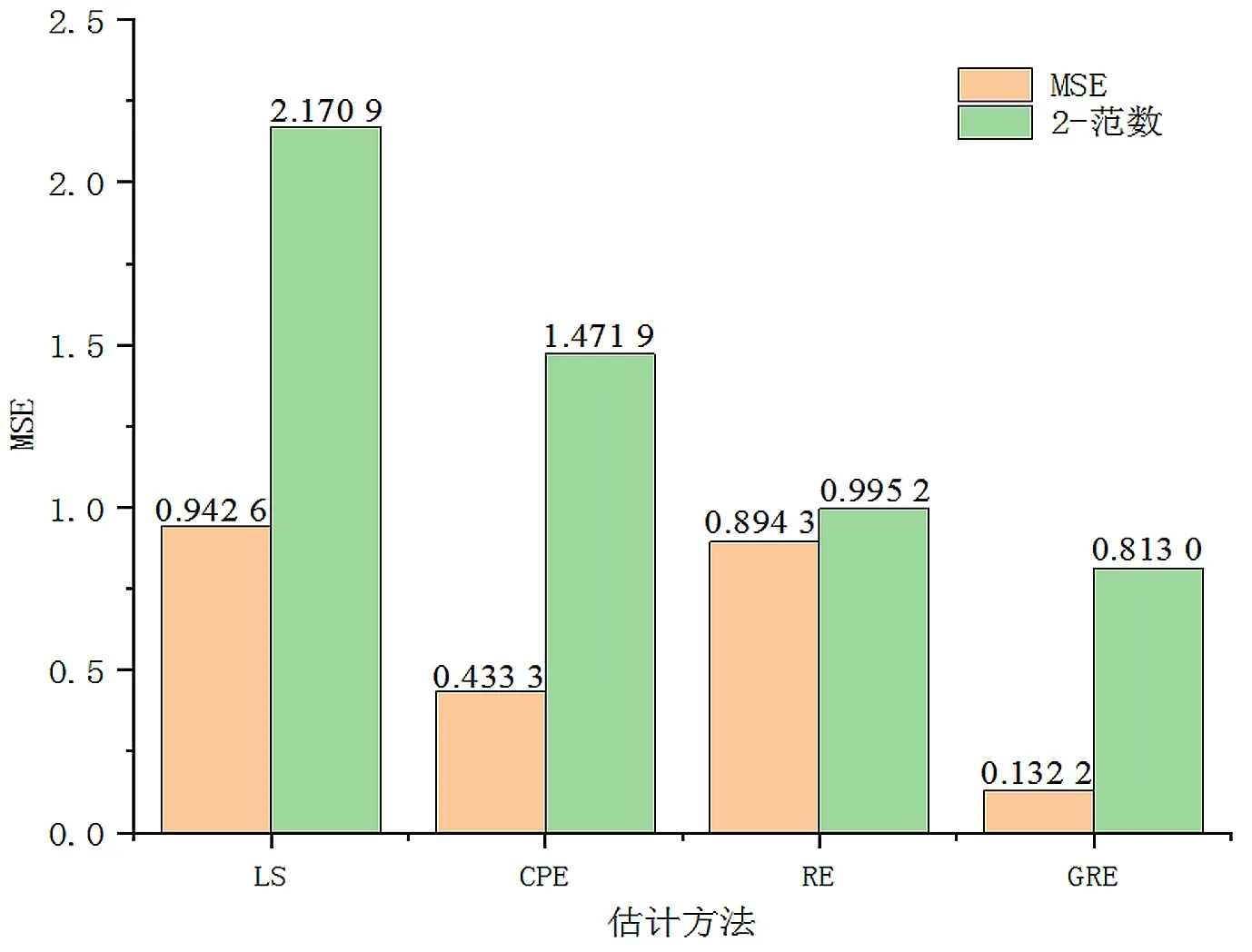
3.2 算例分析
4结论
