共面单脉冲拦截多目标问题

夏存言，张刚，耿云海

哈尔滨工业大学 卫星技术研究所，哈尔滨 150001

随着航天事业发展，在轨航天器之间的交互需求也随之增加，不论是非接触式的相互通信、观测等目的，还是接触式的轨道拦截或交会，均离不开航天器在轨轨道机动。轨道机动从目标约束条件不同可以分为轨道转移、轨道拦截和轨道交会3类。从航天器自身机动方式上又可以分为脉冲机动和连续推力机动。其中轨道转移问题往往不会对机动位置和机动时间做严格约束。但是轨道拦截问题则对终端时刻的位置有着严格的要求，轨道交会问题还同时有着严格的速度匹配要求。

在轨道转移、轨道拦截和轨道交会问题中，轨道转移任务通常只涉及到燃料或时间的优化问题，而轨道拦截和交会任务在现代航天中扮演着越来越重要的角色。不论是需要近距离飞掠或交会的近地小行星探测任务，或是需要近距离观测的大型航天器在轨服务任务及近距离捕捉的空间碎片清除任务，抑或是需要精确拦截的假想空间攻防对抗任务等，都需要轨道拦截策略作为理论研究基础。考虑轨道机动的形式为脉冲机动时，轨道拦截及交会问题即为经典的Lambert问题，对此也已经有很多学者提出了多种有效解决方法，并且在经典Lambert问题的基础上，考虑了长飞行时间的条件，即多圈Lambert问题；以及考虑实际飞行环境中的摄动力影响条件下的受摄Lambert问题。考虑到实际任务中虽然对于终端位置速度等条件有着较为严格的约束，但是对于脉冲时刻及飞行时长等其他条件往往并不会严格要求，所以此类任务通常还会涉及到对于燃料或时间的优化过程。当拦截器与待拦截航天器轨道共面时，还可以考虑当脉冲方向受限情况下的拦截优化问题。

虽然经典的脉冲式轨道拦截问题不论在解法上或者优化过程上都已经得到了较为成熟的发展，但是往往相关理论研究均建立在一次脉冲或多次脉冲对应单一目标的基础之上。然而随着现在航天任务的增多，任务对于低成本、高效率的需求更加迫切。在很多任务中，往往存在着飞掠、拦截或交会多个空间目标的需求。针对大规模目标的拦截或飞掠任务，单次脉冲拦截或飞掠多个目标可以提升任务效率。在实际工程背景下，航天器脉冲机动的次数有时也会有着比较严格的限制，例如，对于传统的固体助推火箭推进系统，难以在轨多次开关机，通常均为一次性推进使用。另外，目前大多数工程应用中，航天器轨道机动需要地面测控系统的支持；脉冲机动次数越多，需要的地面资源越多。

单脉冲拦截多目标这一理论问题，当脉冲时刻和飞行时间均自由时，在理论上存在单脉冲拦截二目标的可行解。而对于共面情况，理论上存在单脉冲拦截三目标的可行解。与传统的单脉冲对单目标不同，该问题增加了一项终端位置约束，使得即使在二体条件下，也无法推导出此问题的完整解析解。在2019年的国际轨道优化设计大赛(GTOC-X)中，“银河系移民”赛题里也包含着单脉冲拦截多目标这一子问题，这一子问题的求解也是竞赛取得高分的一个关键点。竞赛的冠军队伍结果中给出的解决方法是“打靶+优化”。其思路可以概括为先随机给定速度脉冲，然后通过数值积分得到其飞行轨迹，并在赛题给定的10万个备选目标中搜索出与其轨迹接近的目标集，之后再通过对脉冲矢量进行修正得到更精确的拦截解。由于备选目标数量庞大，该方法可以通过搜索有效地得到一系列可行解集。但针对空间中给定的二到三个目标，如何从理论上进行求解，目前并无相关研究报道。

结合前文所述，本文将通过理论推导和研究，将共面条件下的单脉冲拦截二、三目标问题化简总结为求解只包含两个自由变量的非线性方程组问题，并给出求解初值搜索方法，再通过牛顿迭代，得到共面条件下二维方程组的数值解。此外，对于二目标情况，其解不唯一，将通过数值优化得到燃料最优解。

1 问题描述

为表达简洁，问题描述以单脉冲拦截三目标为例，单脉冲拦截二目标的情况可视为在此基础上减少一个待拦截目标和对应终端约束。

考虑地球二体引力模型下飞行轨道共面的4个航天器，包括1个拦截器和3个待拦截航天器,,。需要注意的是，待拦截航天器的编号与拦截目标的编号并无直接对应关系，拦截目标编号以拦截顺序为依据，即若拦截顺序为→→，则目标2为航天器，目标3为航天器(见图1)。

问题中共涉及5个时刻，分别为整体任务的初始时刻、施加脉冲机动时刻、3个目标器的拦截时刻、、。在初始时刻，其初始位置点分别为0,,1,,2,,3,，对应的位置矢量分别为0,,1,,2,,3,。在时刻(≥)，拦截器施加脉冲机动Δ，使拦截器的飞行轨道由其初始轨道变为拦截轨道，并使其在,,(<<<)时刻分别与3个目标完成轨道拦截，如图1所示。求解此问题即为求解脉冲时刻，拦截时刻,,及脉冲矢量Δ。

不难分析，当目标数量为2时，由于共面条件的存在，未知量个数为5个(,,及速度脉冲在平面内的2个分量)，而终端约束方程为4个(即拦截器与目标的位置矢量在平面内2个分量分别相等)。未知量的个数多于约束方程的个数，所以理论上共面单脉冲拦截二目标问题存在无穷多组解，同时也为该问题在固定脉冲时刻或者某一目标的拦截时刻下的求解提供了条件。对应的，当目标数量为3时，未知量个数为6个，终端

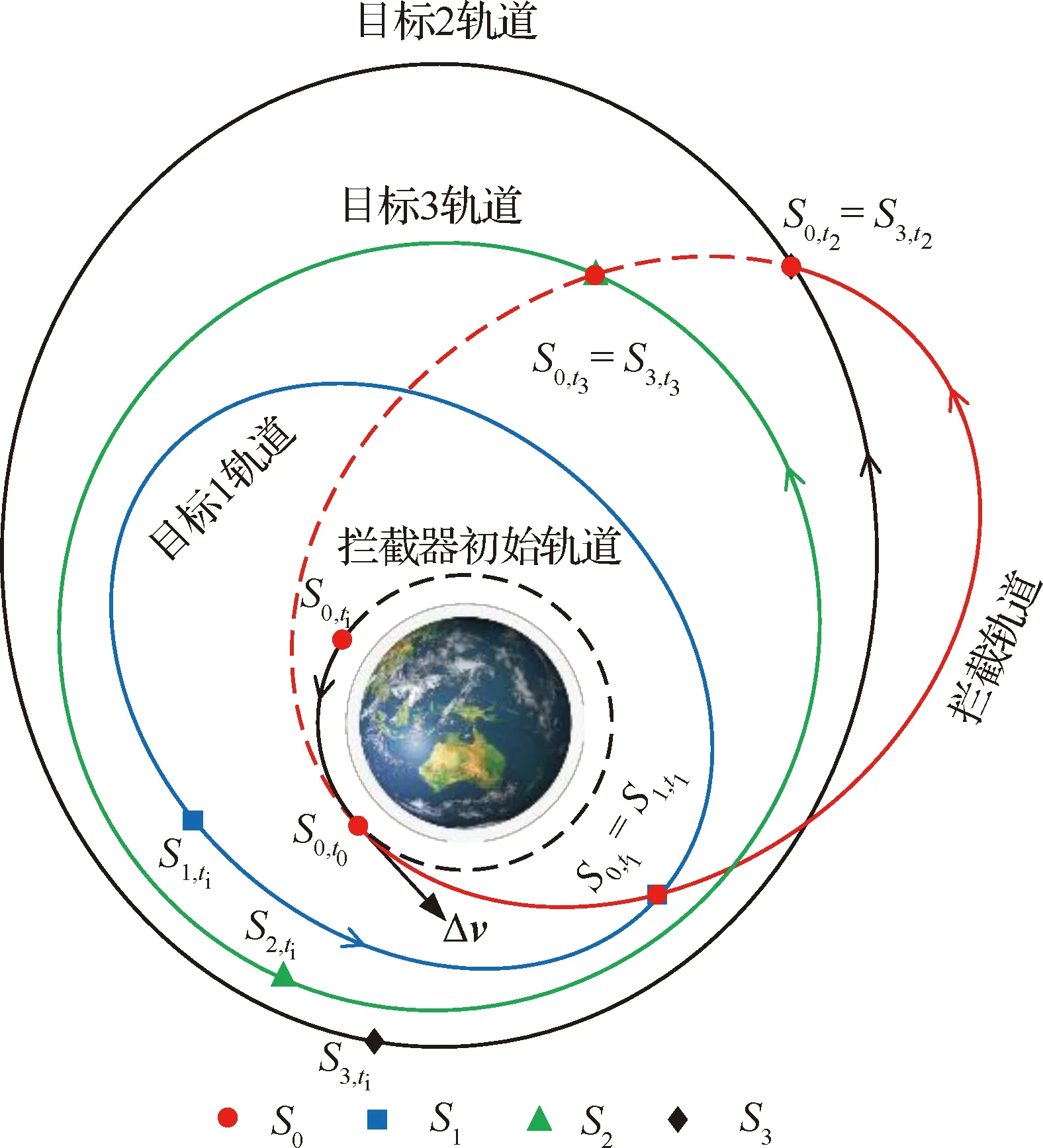
图1 单脉冲拦截二/三目标过程示意图Fig.1 Schematic diagram of two/three-target orbit interception problem with a single impulse

约束方程也为6个，即共面条件下单脉冲拦截三目标问题在给定的范围内，只有有限个数的可行解。

虽然该问题易于定性分析，但是不论是4个或6个方程构成的高度非线性的方程组，在求解时都有着很高的难度和复杂度，并且很难找到合理的初值。所以，如果可以通过轨道理论将自由变量和方程的个数减少，求解过程将得以极大简化。此过程将在之后的内容中具体推导和介绍。需要说明的是，文中所给出的理论方法均建立在二体引力模型下，当考虑J2摄动时，本文方法得到的结果仍可以保证拦截器与目标近距离飞掠。

2 单脉冲拦截二目标

2.1 终端约束非线性方程组

在二体引力模型下，航天器在其轨道某确定真近点角,(=0,1,2,3,4 and=0,1,2,3)处的位置矢量,可表示为

,=,,

(1)

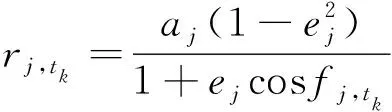
(2)

,=

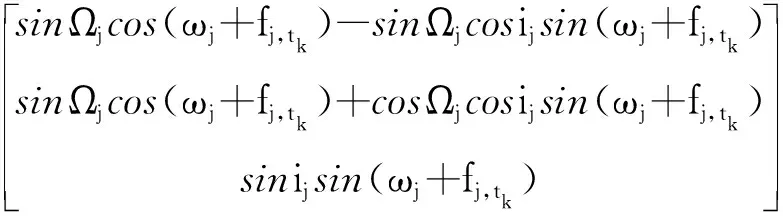
(3)

式中：,为位置矢量,的大小；,为地心惯性系下的位置矢量方向单位矢量；为半长轴；为偏心率；为真近点角；为轨道倾角；为升交点赤经；为近地点幅角。

通过Gibbs三矢量定轨方法可知，在共中心引力体的前提下，3个共面的位置矢量可以确定一条开普勒轨道。考虑到本问题中共面的条件天然满足，因此若,,已知，与之分别唯一对应的3个位置矢量0,,1,,2,即可唯一确定一条航天器飞行轨道，即本问题中的拦截轨道。由Gibbs方法可以推导出拦截器在拦截轨道上对应时刻的速度矢量表达式:

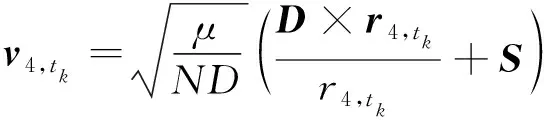
(4)

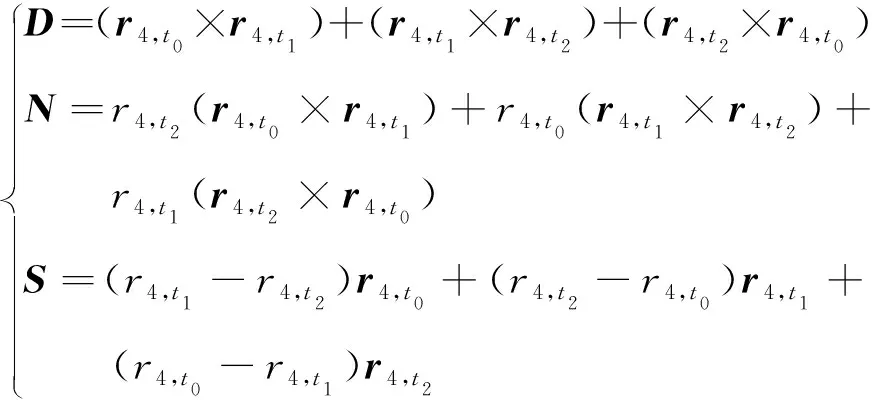
(5)

考虑到拦截所需的终端位置相等，式(5)中的相关矢量有着如下等式关系：

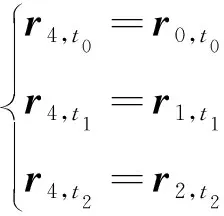
(6)

即式(4)中的所有变量均可表示为关于,,的函数。

通过状态矢量，可以表示出拦截轨道的相关轨道根数：

1) 半长袖

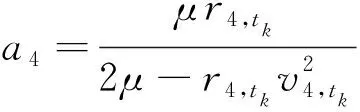
(7)

2) 偏心率矢量

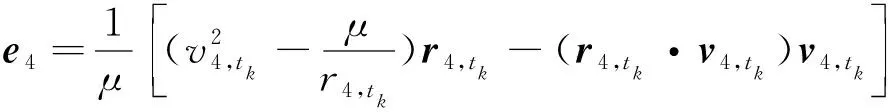
(8)

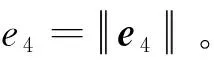
(9)

由真近点角与偏近点角、平近点角间的转换关系可得到对应位置处的平近点角表达式为

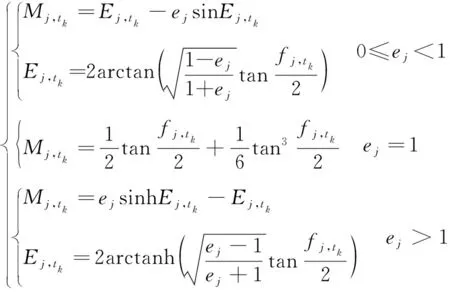
(10)

式中：=0,1,2,3,4且=0,1,2,3。

由开普勒方程建立关于目标1和目标2的终端时刻位置约束方程组：

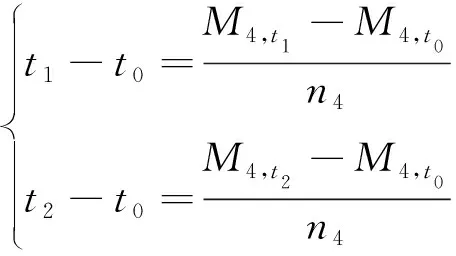
(11)

不难发现，在式(11)中，等号右侧各量均是关于、、的函数，即方程组的自由变量只有、、。所以关于共面单脉冲拦截二目标问题，可以通过Gibbs三矢量定轨方法将其转化为求解包含3个自由变量的二维非线性方程组，即式(11)的问题。但是由于自由变量个数多于方程个数，该方程组在理论上存在无穷多组解，这给此问题人为增加期望的约束条件提供了可能。

通过人为给定、、其中之一，问题便可转换为固定出发时刻或拦截目标之一时刻条件下的共面单脉冲拦截二目标问题。在2.2节中将具体介绍对于此问题的分析和求解过程。

2.2 给定t0、t1、t2之一的方程组求解

方程组(11)可以写为

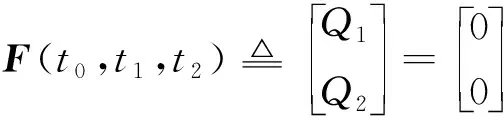
(12)

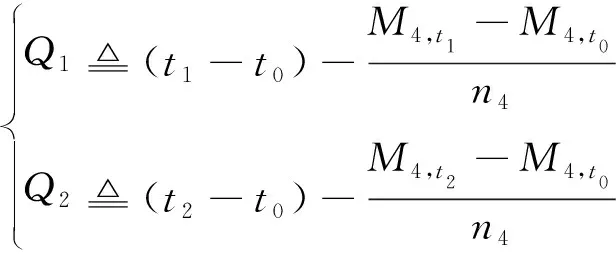
(13)

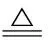
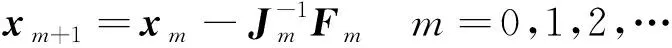
(14)

式中：为方程组的Jacobi矩阵，

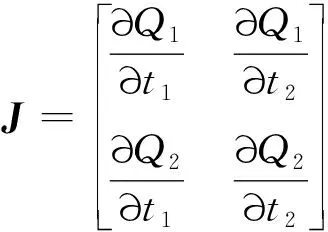
(15)

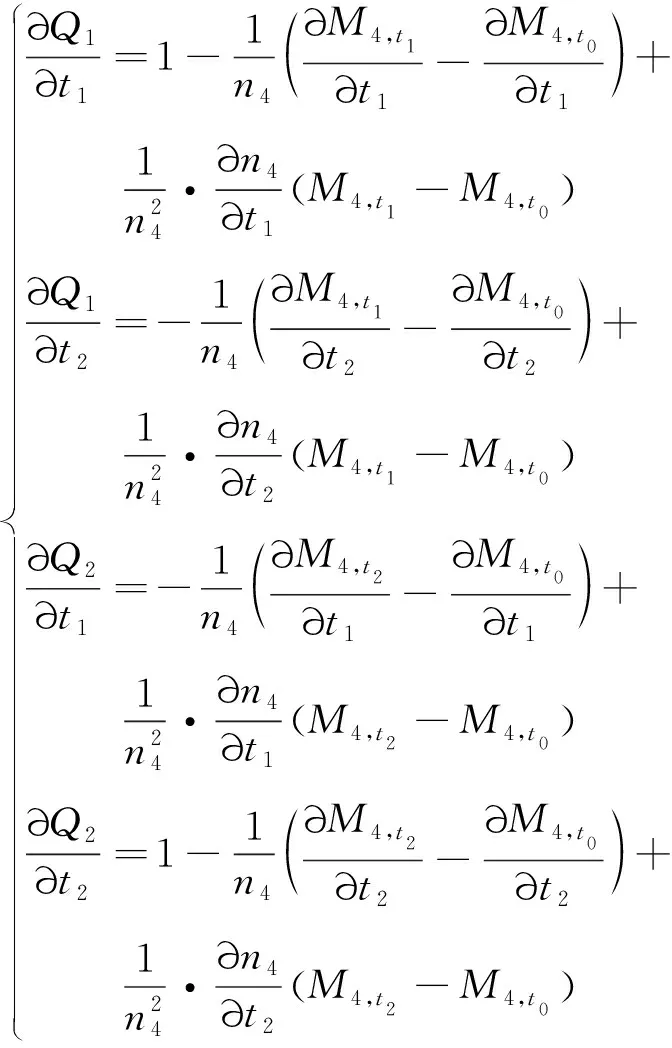
(16)

式(16)中涉及到的各偏导数实际上均可通过数学推导得到解析表示，由于过程较为繁琐，为避免冗繁，在此处不做详细推导。取而代之则可以通过数值方法得到近似偏导数矩阵。2.3节将给出牛顿迭代求解方程组的初值搜索方法。

另外，当3个时刻均自由时，此问题还可以对燃料进行优化求解。如限制脉冲时刻在拦截器一个轨道周期内条件下，传统方法大多由进化算法等全局优化+序列二次规划等局部优化寻得约束条件下的燃料最优解；传统方法的优化变量包括脉冲时刻、拦截两个目标的时刻及共面脉冲向量的2个分量(共5个变量)，终端约束条件是拦截2个目标的位置(共4个方程)。而本文首先针对给定脉冲时刻，求解二维方程组得到经过两目标的解，然后仅优化脉冲时刻，得到燃料最优解，可以使整个问题的维度降低。

2.3 迭代初值搜索

对于此问题而言，由于其非线性程度很高，很难通过理论分析推导给出合理的初值，所以需要借助数值搜索算法进行方程组迭代初值的获取。得益于已经将此问题的自由变量个数减少为2个，经典的等高线图，即PCP(Pork-Chop Plot)搜索算法可以有效地搜索合理的初值点。PCP法是一种在深空探测任务发射窗口搜索中十分重要的方法。通过将给定区间范围的两自由变量按照一定的步长网格化，对每一个网格点计算指标函数值，最后将数据通过等高线图的形式可视化，合理的初值点即可轻松获取。

PCP法对只有2个自由变量的初值搜索问题十分有效，因此同样适用于单脉冲拦截二目标问题。仍以固定脉冲时刻为例，则2个自由变量为、，令搜索的指标函数为拦截两个目标的时间误差之和，表示为

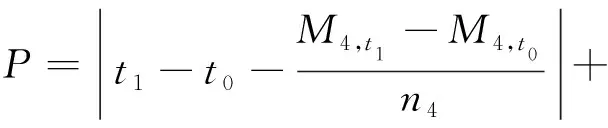
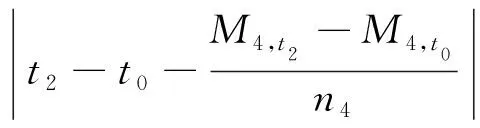
(17)

若足够小，则表示拦截目标1和目标2的时间误差均足够小，与其对应的[,]便可以认为是合理的初值点。

通常来说，传统意义上PCP法搜索初值点是通过人工在等高线图上进行选取。但为了求解计算的程序化，可以为PCP法增加一个筛选的过程，即在对每个网格点计算指标函数值后，若小于给定的容许值(例如500 s)，则该点即可被视为是一个合理的初值点。通过这种策略得到的初值点，大部分都可以在迭代后收敛得到精确的可行解，其余无法收敛至=0的初值点则会被舍弃。最终得到的解，便是在给定区间范围内的所有单脉冲拦截二目标的可行解。

3 单脉冲拦截三目标

与单脉冲拦截二目标不同，拦截三目标时，若仍选择Gibbs三矢量定轨法建立方程组，则易知方程维数和自由变量的个数均为3。虽然数量上只增加了一个，但是对于方程组求解的复杂度来说，其提升是巨大的。如Jacobi矩阵的待计算项将会由4项增至9项，且初值搜索由于自由变量个数增加了一个，导致网格点的数量会增加2～3个数量级。以上条件均表明关于共面单脉冲拦截三目标问题，三矢定轨确定拦截轨道的策略不再适用。所以，为了使该问题同样可以得到充分的简化以便于求解，一种通过Lambert解以减少自由变量个数的策略将在下文中介绍。

需要说明的是，与经典的三脉冲拦截三目标任务相比，单脉冲拦截三目标有着更为严苛的约束条件。对于三脉冲拦截三目标，自由变量包括三次脉冲的时刻、拦截3个目标的时刻、以及三次脉冲分量(共12个变量)，约束方程包括拦截3个目标时位置矢量(共6个约束条件)。对于单脉冲拦截三目标，优化变量和约束方程均为6个。因此，单脉冲拦截三目标问题并不存在优化空间，在一定的时间范围约束下，该问题是否存在解以及存在解的个数，只能通过数值计算得到。

3.1 终端约束非线性方程组

由于增加了1个待拦截目标，使得终端约束方程的数量增加，因此若仍期望使方程的数量为2，则需要令3个终端约束之一始终满足，而Lambert理论则恰好适用。当脉冲时刻以及拦截其中某一目标(以目标1为例)的时刻给定时，通过Lambert算法即可获得一条可以保证满足拦截目标1的拦截轨道，同时由于所有的初始轨道均天然满足共面条件，所以用Lambert算法得到的拦截轨道也必然处在同一平面内。换言之，拦截轨道可以由[,]唯一确定。

当拦截轨道的相关参数确定后，通过共面轨道的相关参数和几何关系，可以得到其与目标2、目标3的轨道交点处各自的真近点角，过程如下。

当两轨道共面时，设两轨道分别以A、B表示，则若二者有交点，交点处有=。由式(2) 可得

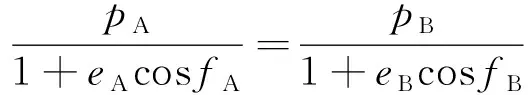
(18)

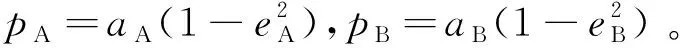
从真近点角的定义可知在交点处两条轨道上的真近点角满足如下关系：

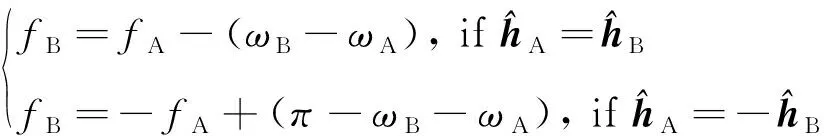
(19)

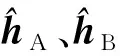
令

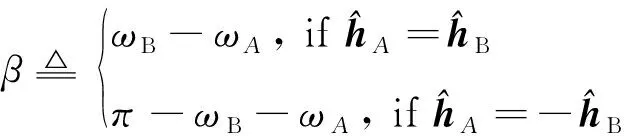
(20)

则结合式(19)，可将式(18)变换为

+cos+sin=0

(21)

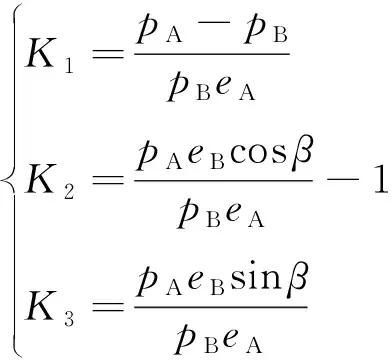
(22)

由三角函数关系求解方程(21)，并结合式(19) 即可求得及。通过以上分析，令拦截轨道为A轨道，目标2、目标3的轨道分别作为B轨道，则可以得到拦截轨道与目标2、3轨道交点处各真近点角4,,4,,2,,3,。通过式(10)转至平近点角，并建立相应的开普勒时间方程为

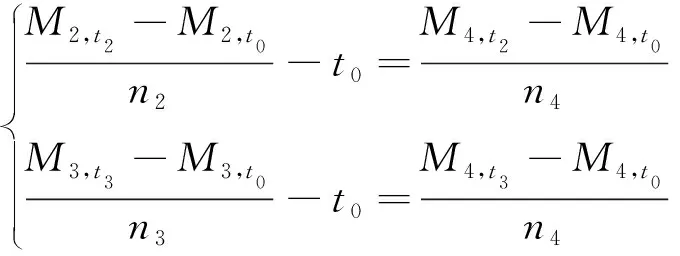
(23)

在方程组(23)中，所有变量都是关于,的函数。通过加入Lambert方法，将共面单脉冲拦截三目标问题也转化为求解只包含两个自由变量的非线性方程组的问题。与2.1节中单脉冲拦截二目标的不同之处在于，式(23)中的各变量虽然是关于,的函数，但是由于Lambert问题的求解算法并不是完全解析的，导致式(23)的方程组无法解析表示，从而无法推导出其解析形式的Jacobi矩阵，只能通过数值方法近似得到其Jacobi矩阵再进行牛顿迭代求解。

虽然求解过程只能使用数值方法，但是由于自由变量的个数为2，相比于3个自由变量的情况，综合考虑初值搜索和求解的复杂度，该方法仍然有着明显的优势。

3.2 方程组数值求解

方程组(23)可写为

(24)

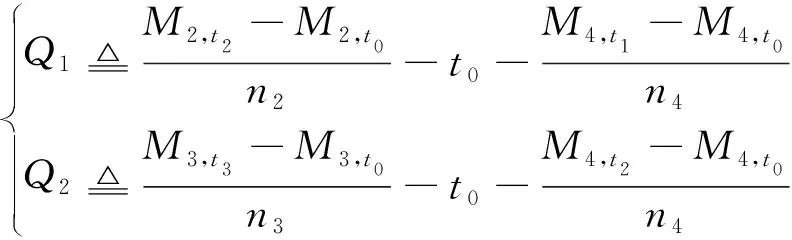
(25)

3.3 迭代初值搜索

对于单脉冲拦截三目标问题，由于3.1节中工作已经将问题的自由变量个数如拦截二目标一样减少为2。所以初值搜索仍然可以选择2.3节中介绍的Pork-Chop图法。只需将指标函数的形式改写为

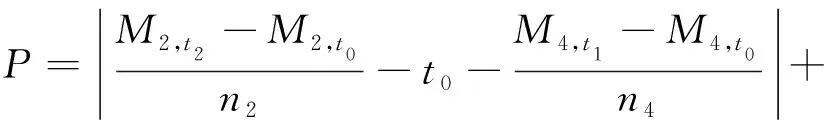
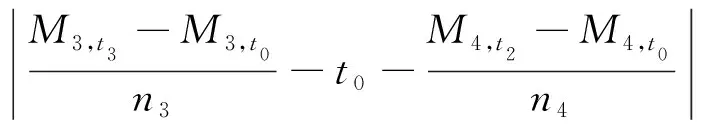
(26)

由式(26)为指标搜索得到的初值点即可代入迭代方程对方程组进行求解。值得注意的是，对于单脉冲拦截三目标问题，虽然通过引入Lambert理论将自由变量个数减少为2个，但是对于问题本身，其终端约束仍然比拦截二目标更强，以至于在较短的时间范围内(如拦截器初始轨道的一个轨道周期内出发，目标2的一个轨道周期内拦截)，有可能出现无法搜索到合理初值点的情况。所以，对于单脉冲拦截三目标问题，在初值搜索时，若难以寻得合理初值点，可以考虑在满足任务要求的前提下，将搜索区间适当扩大以寻求可行解。

4 仿真算例

4.1 单脉冲拦截二目标

针对单脉冲拦截二目标问题，初始拦截器及二目标轨道参数如表1所示。

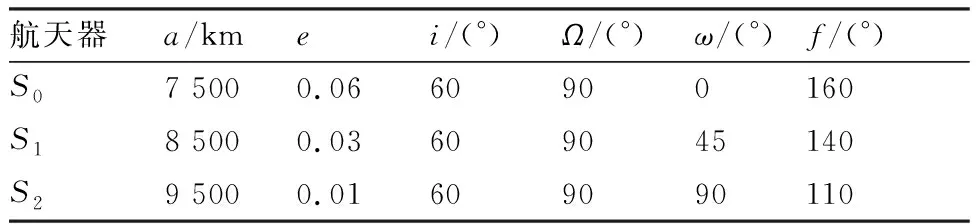
表1 拦截二目标问题初始轨道参数

以给定脉冲时刻为例，对拦截目标1和目标2的时间,进行搜索，值得注意的是，由于对于拦截顺序并没有约束，所以目标1既可以是，也可以是。以目标1为为例，令脉冲时刻=1 500 s，对于目标1和目标2的搜索的时间区间分别为(,]、(,],,分别为目标1、目标2的一个轨道周期。搜索时间步长为100 s。将初值搜索结果中>1 000 s的结果舍去，从而形成等高线图，结果见图2。

从图2中可以看出，当以为目标1时，脉冲时刻固定为1 500 s条件下，有着可以使指标函数足够接近0的点，而在这些点处对应的及则可以视为足够接近精确解，可作为求解方程组的初值点。

需要说明的是，在实际的仿真求解该问题的过程中，绘制等高线图的过程是不必要的，只需要通过程序选择指标函数<500 s的点作为初值集合即可。此处给出等高线图仅供读者便于理解此过程。

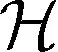
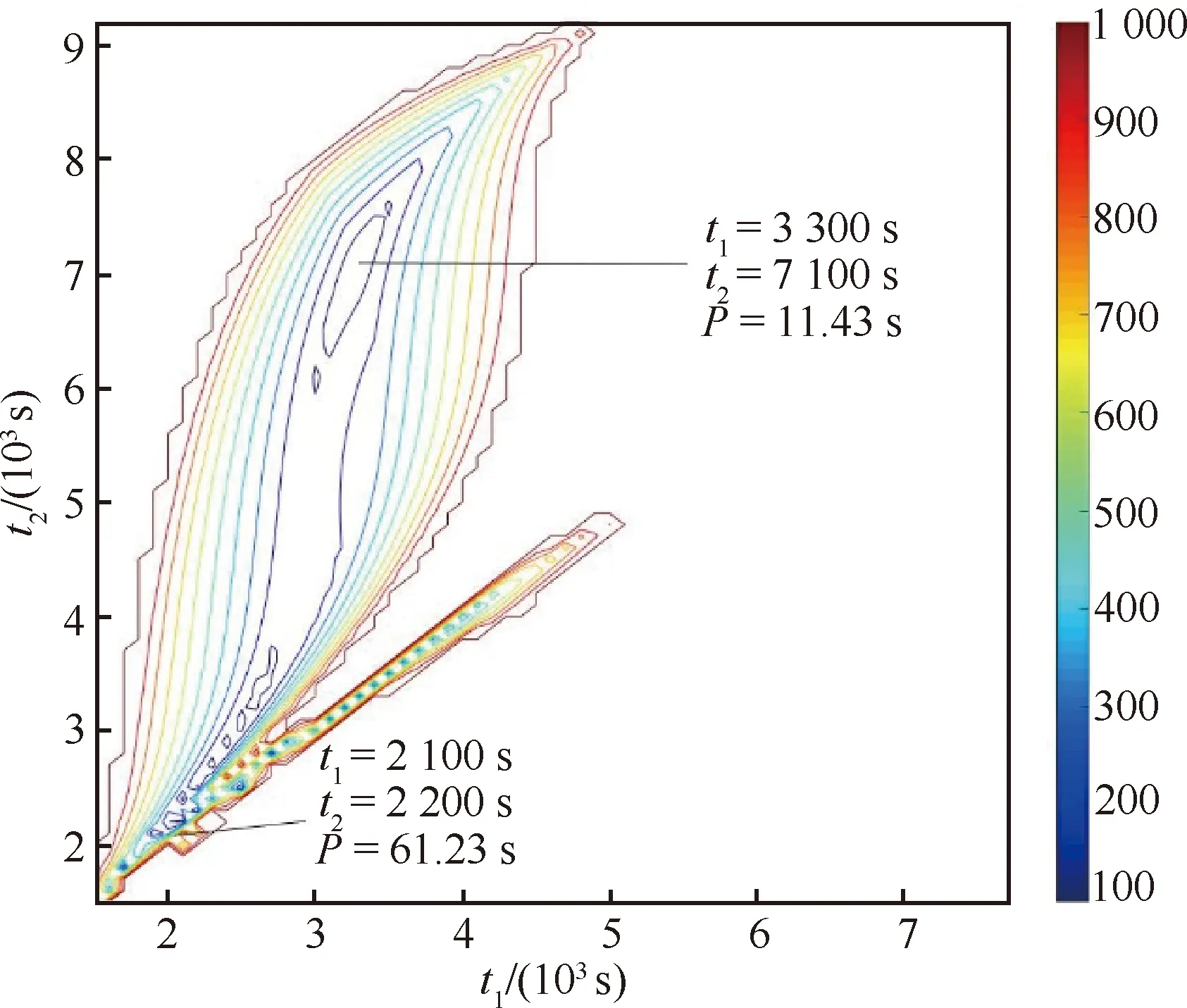
图2 S1为目标1条件下初值搜索等高线图Fig.2 Contour map of initial value search with S1 as target 1

表2中，1号解的结果是一条双曲线轨道，虽然速度增量远远超过实际应用可以接受的范围，但这也只是针对如表1的初始条件以及前文介绍的相关约束条件下的特殊情况，仍然可以说明本文对该问题的相关研究同样适用于拦截轨道为双曲线轨道的情况。2号解及3号解的速度增量则分别为3.777 km/s 及0.534 km/s。相应的拦截所需时间也依次增加，在实际工程应用时则可以根据任务需求，综合燃料及时间因素进行选择。

同时，可以看出在本文的条件设置下，该问题的解中没有拦截顺序为→→的情况，这说明在初值搜索时便没有使指标函数足够小的点，说明对于以为目标1的情况，在给定的时间约束条件下，没有可以实现单脉冲拦截二目标的解。

以表2中1～3号解中的速度增量最小的3号解为例，绘制航天器飞行轨迹如图3所示，可以看出拦截器在脉冲后与二目标实现了精准拦截。

表2 拦截二目标问题解集Table 2 Solutions of two-target interception problem

注:序号1～3为固定脉冲时刻=1 500 s条件下的解;序号“*”为燃料最优解

图3 最小速度增量解飞行轨迹Fig.3 Trajectories of the minimum-fuel solution

另外，考虑到单脉冲拦截二目标的脉冲时刻可以任意给定，所以在一定的时间区间约束下，可以对所需燃料进行优化，并得到对应的燃料最优解。例如在拦截器的一个轨道周期内施加速度脉冲并寻找燃料最优解，则可以通过将脉冲时刻按一定步长搜索，得到相应的最小脉冲随脉冲时刻变化曲线。针对表2所示初始参数，以10 s为步长，画出相应曲线如图4所示。

从图4可以看出，对于给定的初始轨道参数，单脉冲拦截二目标所需的最小速度增量随拦截器脉冲时刻变化在大部分情况下可认为是连续的，且可以从结果数据中得到近似最小速度增量解，在其附近减小步长即可搜索得到最小速度增量解，见表2中序号“*”。可以看出最小速度增量解所需速度增量为0.520 km/s，相比于本节设置的1 500 s脉冲时刻初始条件下求得的最小速度增量0.534 km/s所需燃料更少。

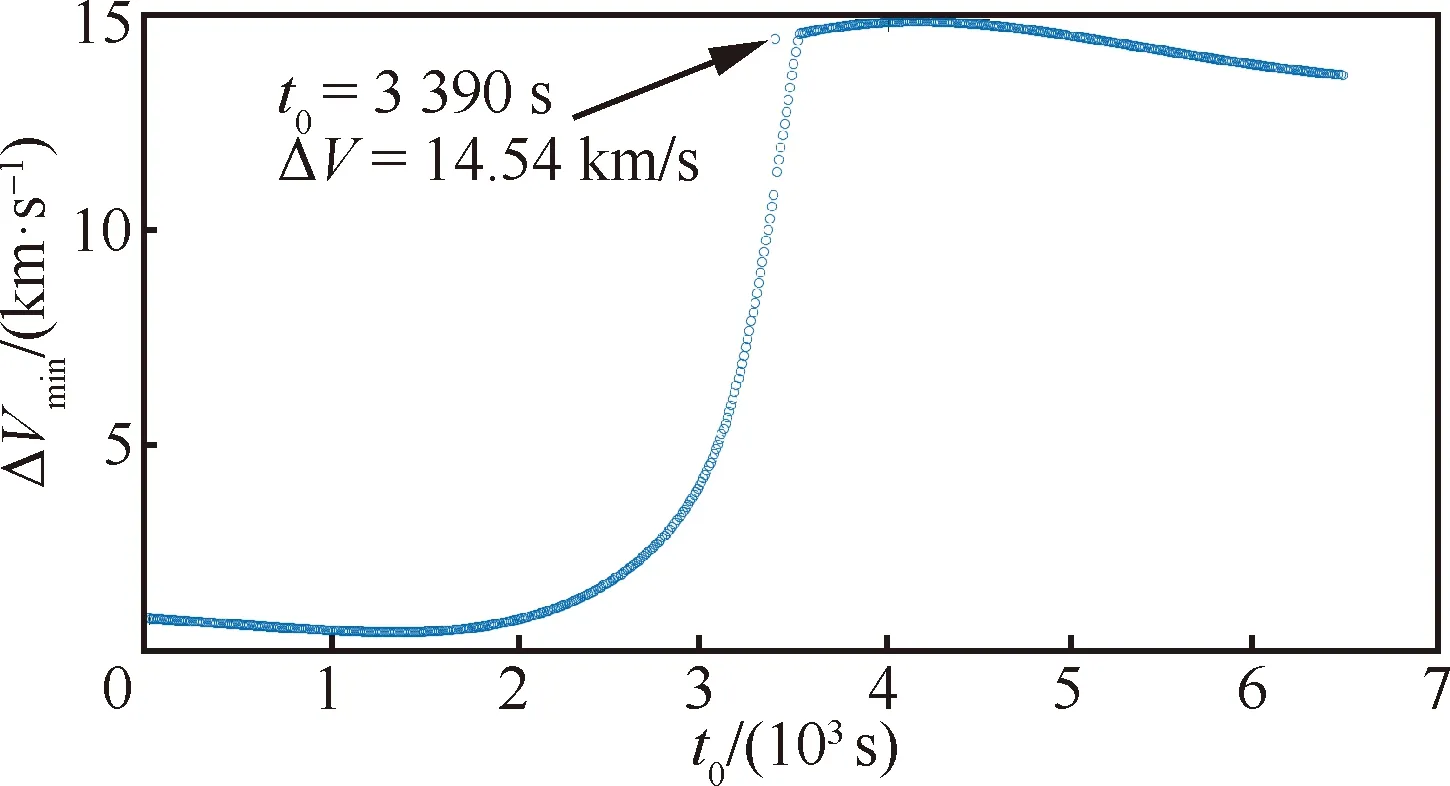
图4 最小速度增量随脉冲时刻变化曲线Fig.4 Minimum-fuel solution with different impulse times

另外，图4中=3 390 s时，最小脉冲出现“跳跃”的情况，是由于此时刻附近求解得到的拦截轨道偏心率趋近于1，从惯性系中观察，轨道的运行方向即将反向，拦截轨道的轨道倾角即将从60°跳变为120°(同时升交点赤经由90°跳变为270°)所致。

4.2 单脉冲拦截三目标

对于单脉冲拦截三目标问题，初始轨道参数如表3所示。

由于拦截顺序并不作约束，单脉冲拦截三目标问题的拦截顺序与拦截二目标相比选择性更多。考虑到理论求解方法一致，所以在此处仅以其中一种拦截顺序为例，拦截顺序为→→→。首先对此情况进行初值搜索，令脉冲时刻范围在的一个轨道周期之内，即∈[0,]，拦截的时刻在的一个轨道周期之内，即∈(,]。搜索步长100 s，舍去>1 000 s 的点，得到等高线图结果如图5所示。求解得到单脉冲拦截三目标结果见表4。

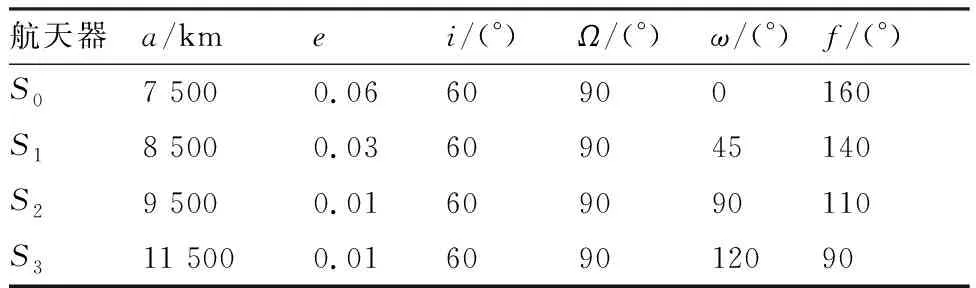
表3 拦截三目标问题初始轨道参数

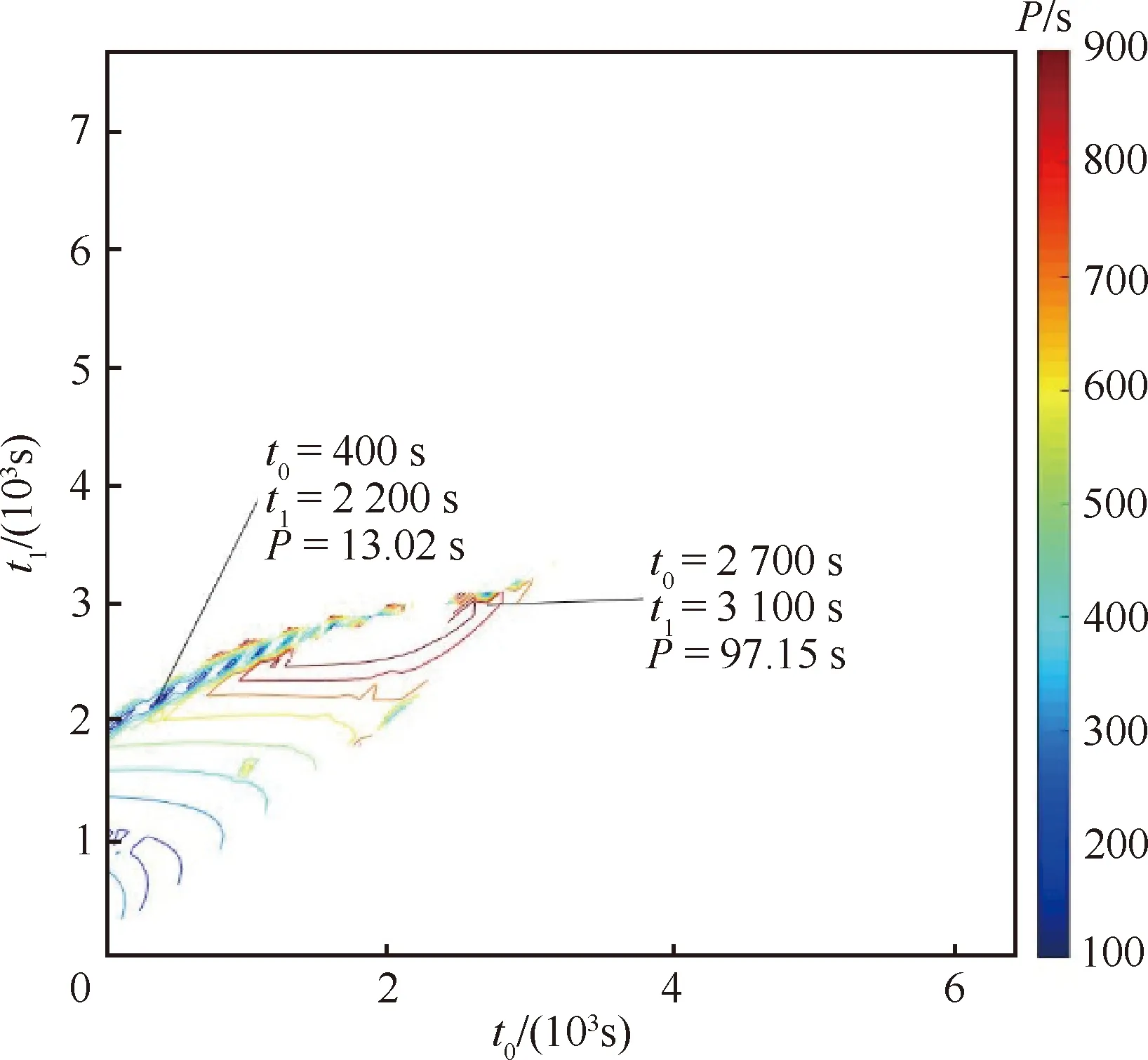
图5 拦截三目标问题初值搜索等高线图Fig.5 Contour map of initial value search of three-target interception problem

以表4中1号解为例，绘制航天器飞行轨迹如图6所示。从图中可以看出，拦截器成功通过一次脉冲实现了对3个目标的拦截。

表4 单脉冲拦截三目标问题解集Table 4 Solutions of three-target interception problem

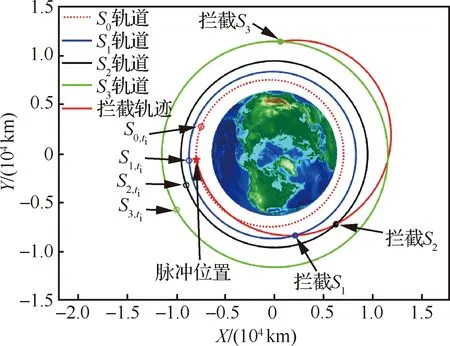
图6 拦截三目标问题飞行轨迹Fig.6 Trajectories of three-target interception problem

4.3 针对三目标拦截的单脉冲和三脉冲结果比较

由于三脉冲拦截三目标由于有着6个维度的自由变量空间，可通过全局优化算法(如遗传算法等)得到最优解。针对本文的特定初始轨道参数，给出单脉冲拦截三目标的可行解与三脉冲拦截三目标优化解的对比结果，结果见表5。结果表明，当拦截所有目标的任务总时长约束在的1或2倍轨道周期内时，遗传算法得到的燃料最优解与本文单脉冲拦截三目标的结果一致。但是当时间约束放宽至3或4倍时，遗传算法得到的优化解优于单脉冲拦截三目标的结果。

值得注意的是，单脉冲拦截三目标问题解的存在性与最优性与初始轨道直接相关，在某些初始条件下存在解，并且可能是较短时间约束下的最优解；但在某些初始条件下不存在解，或单脉冲解所需燃料大于多目标解。在实际工程应用中，可根据脉冲次数和脉冲大小等实际因素进行方案选择。

表5 针对拦截三目标的单脉冲和三脉冲结果对比Table 5 Comparison of single-impulse and three-impulse three-target interception results

5 结 论

本文通过分析固定脉冲或拦截某一目标时刻的情况，对共面单脉冲拦截二目标问题进行了求解。对于二目标的情况，其解不唯一，通过分析求解得到了燃料最优解。同时对于脉冲时刻及拦截时刻均自由条件下的共面单脉冲拦截三目标问题进行了分析和数值求解。在二体模型下，分别利用Gibbs方法、Lambert理论，将2个理论问题转化为仅含两个自由变量的非线性方程组的求解问题。之后分别通过解析推导、数值计算得到二者的雅各比矩阵，并通过牛顿迭代实现了问题的求解。初始猜测由等高线图法给出。采用提出的单脉冲多目标拦截方法，在二体模型下实现了二/三目标的精确拦截。数值结果表明，在一些初始条件和时间约束下，本文提出的单脉冲拦截三目标方法的解与三脉冲拦截三目标数值优化解相同。