基于压力插值/力等效混合的火箭结构流-固载荷转换方法
2022-04-26樊一达毛玉明舒忠平王吉飞张洋洋于哲峰
樊一达,毛玉明,舒忠平,王吉飞,张洋洋,于哲峰,*
1.上海交通大学 航空航天学院,上海 200240 2.上海宇航系统工程研究所,上海 201109 3.上海飞机设计研究院,上海 201210
运载火箭在飞行中受到的外载荷包括发动机的推力、飞行气动力、阵风载荷等。在计算运载火箭的动力学响应时,往往将火箭简化为一维梁模型,并将各种外载荷转换为各横截面上的轴力、弯矩等内力,由于这种转化结果比较粗略,在结构设计时需要预留较大的安全裕度。而为了应对不断增长火箭结构轻量化设计需求,应采用更为精细的三维结构有限元模型计算部件载荷,这对于结构优化、减重具有很大意义。此时就需要把气动载荷数据转换三维结构模型上,火箭气动模型与实际结构外形相同,其表面有许多凸起整流罩,而结构模型往往只建立主要承力结构,其表面形状较气动模型而言更为简单,并且气动模型与结构模型网格疏密程度也不同。这就产生了气动载荷转换为结构载荷的问题,即流-固载荷传递问题。
在过去的半个世纪中,国内外学者针对这种不匹配网格之间的数据传递问题提出了多种插值方法来解决,如反距离插值法(Inverse Distance Weighting Interpolation, IDW)、Kriging方法和径向基函数法(Radial Basis Function,RBS)等。Frank对多种插值方法进行了精度和计算效率的比较,结果表示径向基函数法的综合表现较好。吴宗敏和Buhmann从数学的角度分析了不同基函数的径向基函数特性。Harder和Duchon等先后提出了无限板样条(Infinite Plate Spline, IPS)、薄板样条法(Thin Plate Spline, TPS),也都是径向基函数中的一种,其中TPS法是航空宇航工程中最普遍使用的一种插值方法。
力等效是将一个集中载荷等效分配到若干点上的方法。王专利和徐建新等证明了该方法的可靠性。高尚君等提出了一种基于弹簧-悬臂梁模型最小变形能的气动载荷分配方法,解决了气动压力点与部分结构网格节点重合而导致的难以求解的问题。
压力插值法具有局部载荷等效程度高的优点,但要求结构模型外形与气动模型外形保持一致。而力等效法可以保证载荷转换区域总的合力和合力矩等效,并且当结构模型外形与气动模型不一致时仍然适用,但局部载荷未必等效。因此,本文针对简化后、无次要承力部件的结构模型外形与气动模型外形不一致的问题,提出一种压力插值与力等效混合使用的流-固载荷转换方法,即结构模型外形与气动模型外形一致的区域使用压力插值法,不一致区域用力等效法。本文先简要介绍样条插值法和力等效法的原理,然后阐述混合法的原理,最后给出某算例验证的结果。
1 载荷转换原理
1.1 TPS法原理
TPS法是一种三维插值方法,适用于曲面插值,由薄板受分布载荷引起弯曲小变形的模型推导得出,其微分方程为
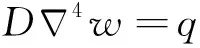
(1)
式中:为板的抗弯刚度,为板的变形。引入球坐标=sincos,=sinsin,=cos,式(1)的基本解设为
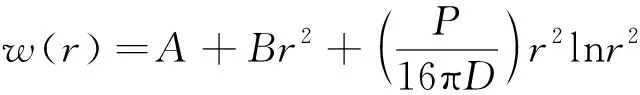
(2)
式中:和是待定系数;为集中载荷。对于作用在(,,)处的个集中载荷,=1,2,…,,板的总变形为基本解式(2)的叠加,可表示为
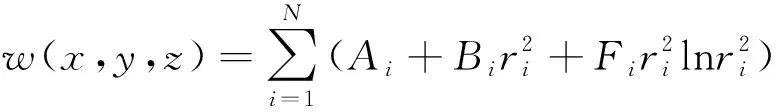
(3)
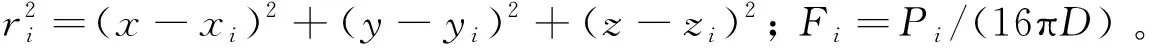

(4)

此时,式(4)的+4个未知量(,,,,,,…,)可由力系的平衡方程以及个已知插值点的位移 的方程求出,即
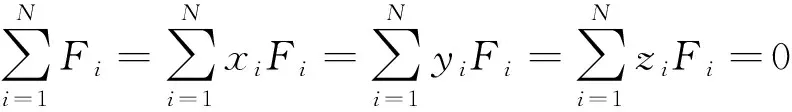
(5)
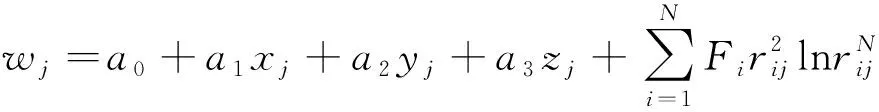
=1,2,…,
(6)
将式(5)和式(6)写为矩阵形式,得到含+4个未知数的线性方程为


(7)
求解式(7),可求出,,,,,…,,同时把待插值的坐标一起代入式(4)可得待插值点的解。
1.2 力等效法原理
力等效法是将一个集中载荷等效分配到若干点上的方法。其基本规则是离气动载荷点近的节点分配到的载荷多,远的分配到的少,且保证分配前后的合力、合力矩不变。本文采用基于弹簧-梁模型的方法进行力的等效转换,避免结构单元中心点位置与气动压力点位置相距过近时产生计算误差过大的问题。
首先假设在-平面内,载荷方向同升力方向。假设某点的气动力为,则合力、合力矩等效方程为
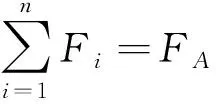
(8)

(9)
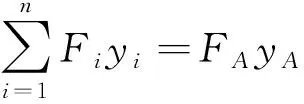
(10)
式中:为要等效的结构单元中心点数;、为结构单元中心点的坐标;、为气动压力点的坐标。
假设各个有限元节点和气动压力点之间有一根“悬臂梁”,在气动载荷点用一个弹簧约束其滑动,其他方向位移固定,设其自由端上的有限元节点分配到的载荷为,此时其变形能为
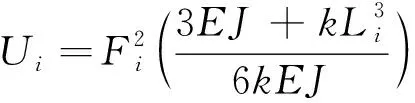
(11)
式中:为假想梁的长度;为假想梁的抗弯刚度;为弹簧弹性系数。
此时假想梁和弹簧的总变形能为
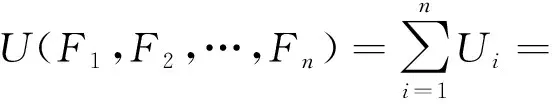

(12)
为使系统的变形能最小,可采用拉格朗日乘子法建立拉格朗日函数
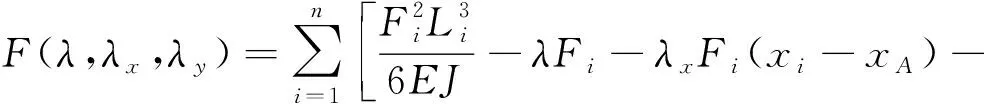
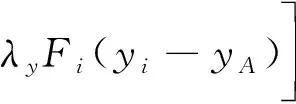
(13)
式中:,,为Lagrange乘子。
为方便计算,可令3=1,将式(13)分别对求偏导并令其为0,得
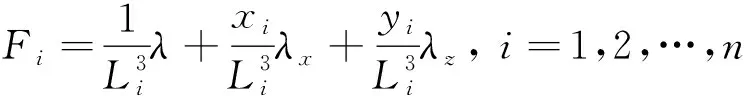
(14)
将式(14)代入式(8)~式(10),并令=(3)得到简化后的方程组为
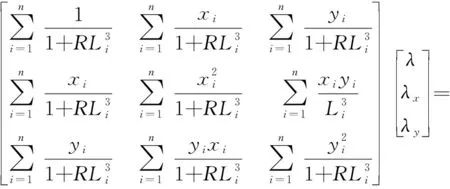
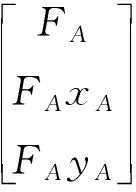
(15)
解出、、后,回代式(14)中即可得到各有限元节点所分配到的载荷。
2 混合法原理
火箭表面的凸起处通常是气动模型和结构模型外形不一致区域。某型运载火箭表面形状的局部如图1所示。因此考虑通过分析气动压力点距轴心的距离来判断气动压力点是否位于表面凸起处。
对于具有复杂表面的火箭结构,分别从火箭气动和结构模型中导出气动压力点信息与结构单元信息,对于每个气动压力点,沿轴向查找距其最近的2个结构单元中心点,分别对比这几个点到火箭轴心的距离,从而判断该气动压力点是否在结构模型表面上,实现气动外形与结构外形一致和不一致区域的划分。对于气动外形与结构外形一致的区域采用压力插值法,而对于外形不一致区域采用力等效法,最终结构模型的载荷为2种载荷的叠加。
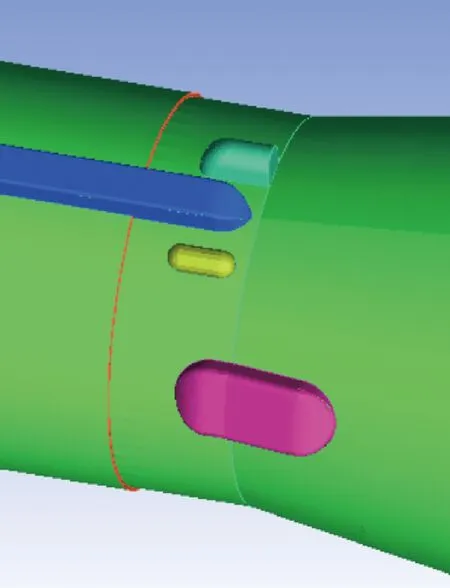
图1 火箭外形细节图Fig.1 Detail drawing of rocket shape
2.1 区分气动压力点
首先计算出每个气动压力点、结构单元中心点到火箭轴心的距离。由于火箭沿轴向直径会变化,因此查找每个气动压力点与沿轴向距该点最近的2个结构单元中心点,并且这2个结构单元中心点分别位于气动压力点左右两侧,采用点斜式建立上述2个结构单元中心点组成的直线方程,通过该方程求出气动压力点所在位置处的基准半径,如图2所示。比较气动压力点的基准半径与实际半径:
|-|>
(16)
式中:为判断一点是否在面内的临界值,本文中取0.005 m,相当于气动模型中的最小网格尺寸。
该研究参考AWL,采用语料库技术,以国内使用甚广的大学英语教材《新视野》为研究对象,计算此套教材的AWL覆盖率,试图回答以下四个具体问题:
如若满足式(16),则认为该气动压力点位于凸出区域,即该点与结构模型不一致,反之,则认为该点与结构模型外表面一致。

图2 识别不一致气动压力点的方法示意图Fig.2 Schematic diagram of identification method for inconsistent aerodynamic pressure points
2.2 区分结构单元中心点
将第1步中区分出的不一致区域的气动压力点投影到基准半径的圆环上,如图3所示,其中
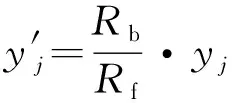
(17)

(18)
式中:、为面外气动压力点的坐标值;′、′为面外气动压力点投影到面内后的坐标值。
将距投影点最近的结构单元中心点作为不一致区域的结构单元中心点,其余点作为一致区域的结构单元中心点。
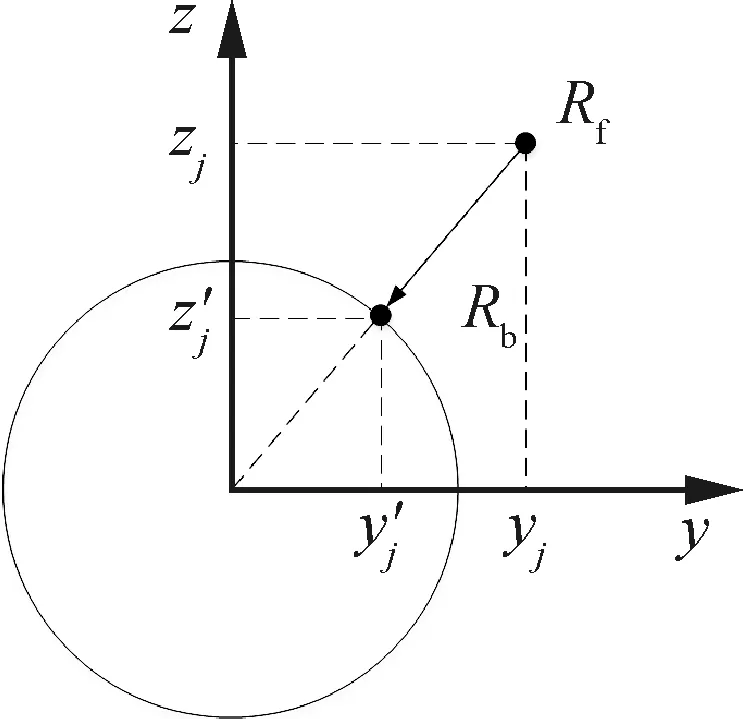
图3 面外气动压力点向面内投影过程Fig.3 Projection process from aerodynamic pressure point out of plane to rocket surface
2.3 用两种方法分别计算对应区域
首先使用TPS法对第1步中输出的一致区域的气动压力点与第2步输出的一致区域的结构单元中心点插值,得到一致区域的结构单元中心点的压力。
然后使用力等效法转换不一致区域的气动力。先将不一致区域气动压力点的压力乘单元面积转换为气动力,然后根据结构单元中心点的信息找到对应的结构网格节点,采用力等效法进行载荷转换,得到结构网格节点上所受到的力。
3 算 例
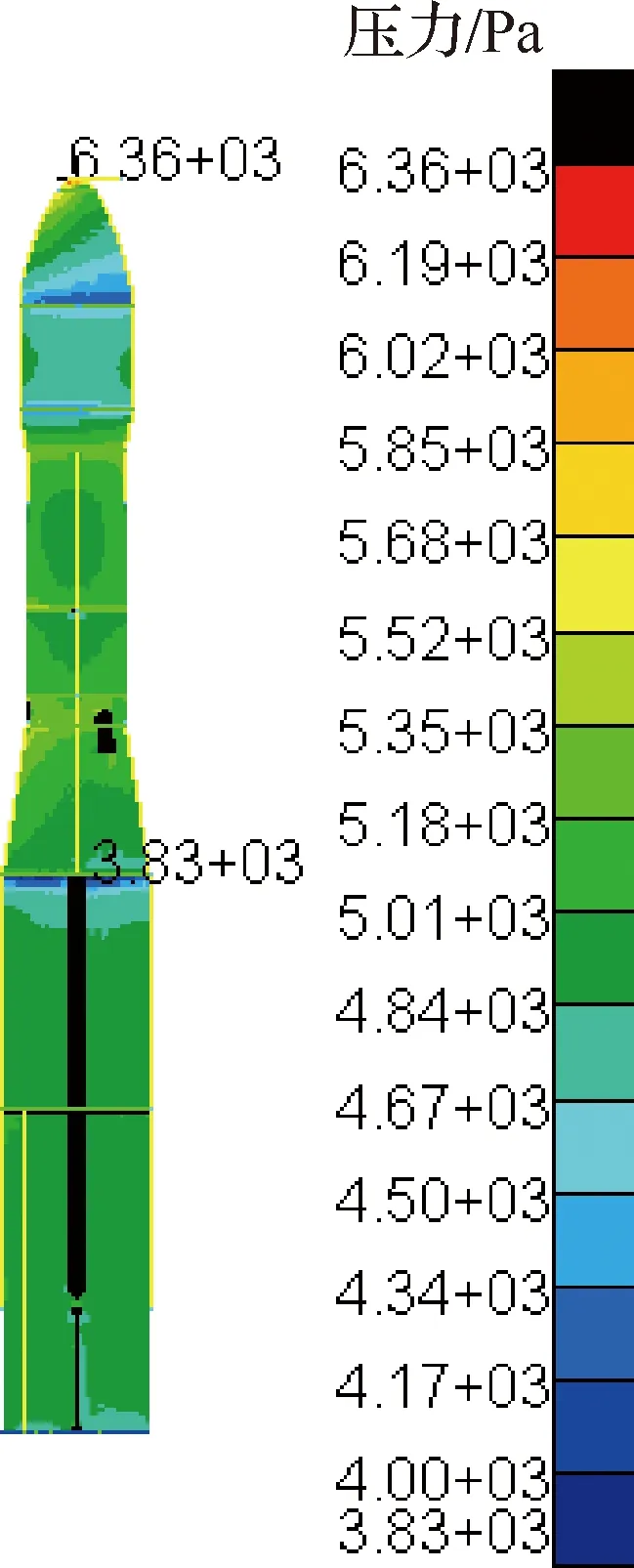
本文的算例为某型运载火箭,气动模型在FLUENT中建立,火箭外形及气动载荷压力分布如图4所示,表面气动压力点共614 209个。结构模型在PATRAN中建立,结构有限元模型网格如图5所示,表面结构单元共41 596个,结构网格节点共39 951个。

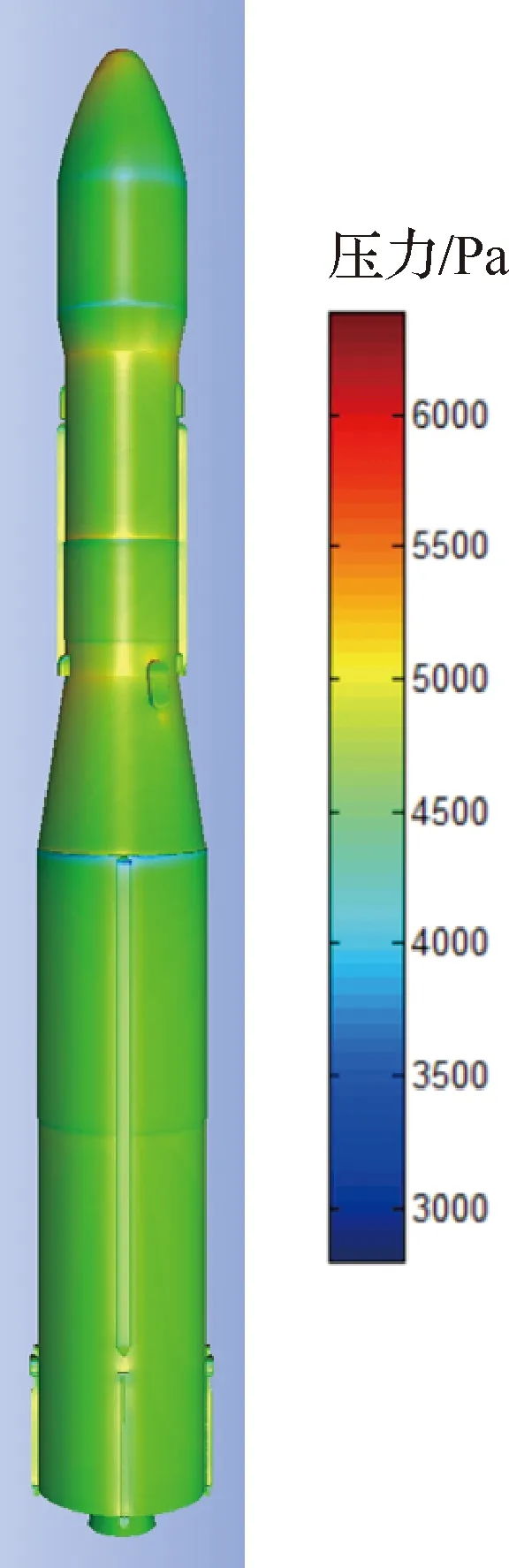
图4 火箭外形及气动压力分布图Fig.4 Launch vehicle shape and aerodynamic pressure distribution
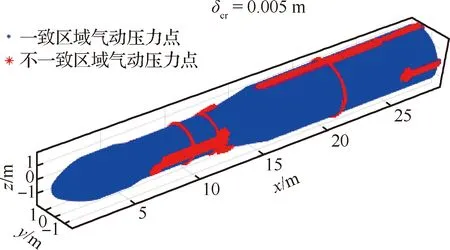
图6 气动压力点整体分布图Fig.6 Overall distribution of aerodynamic pressure points
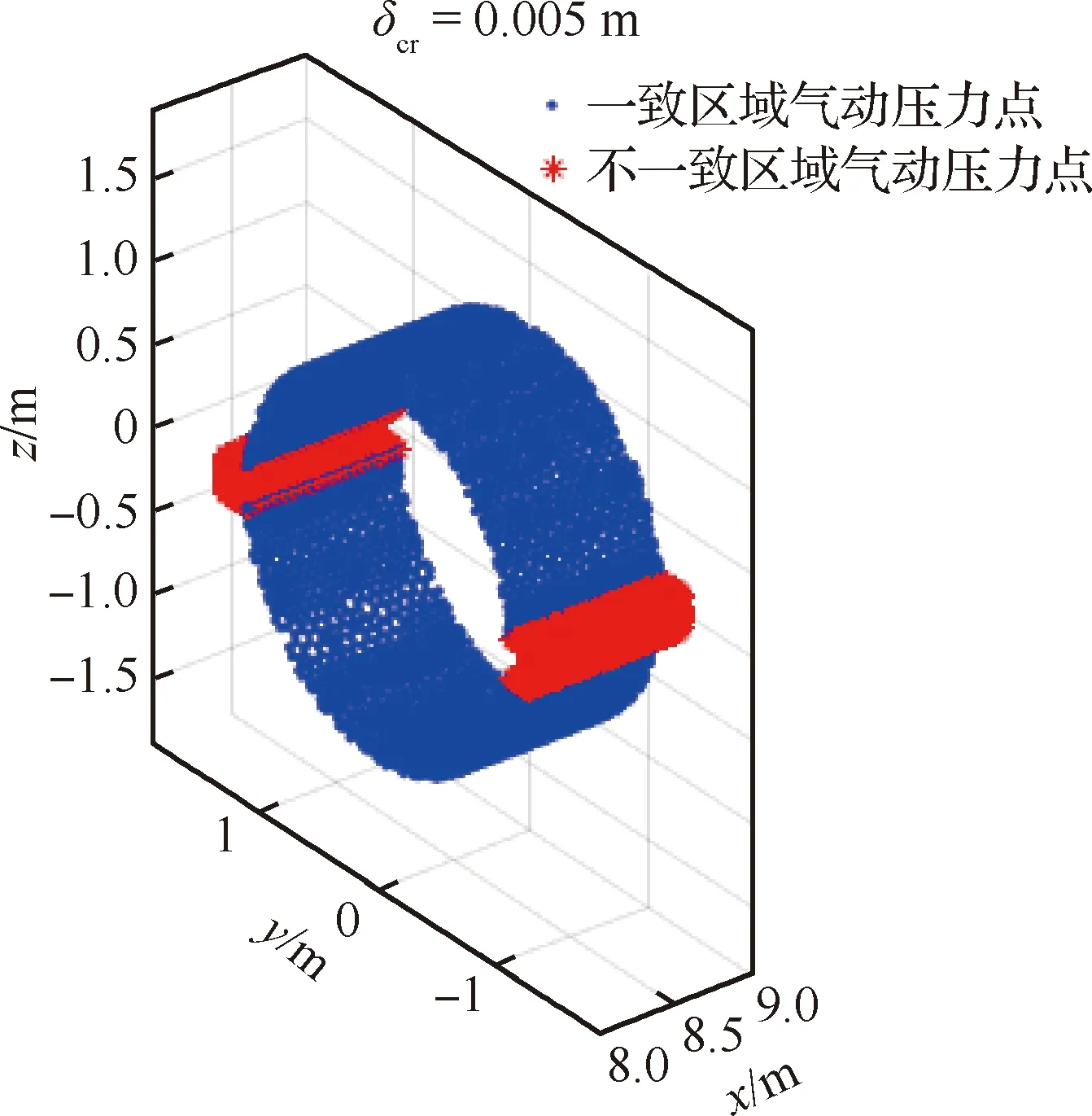
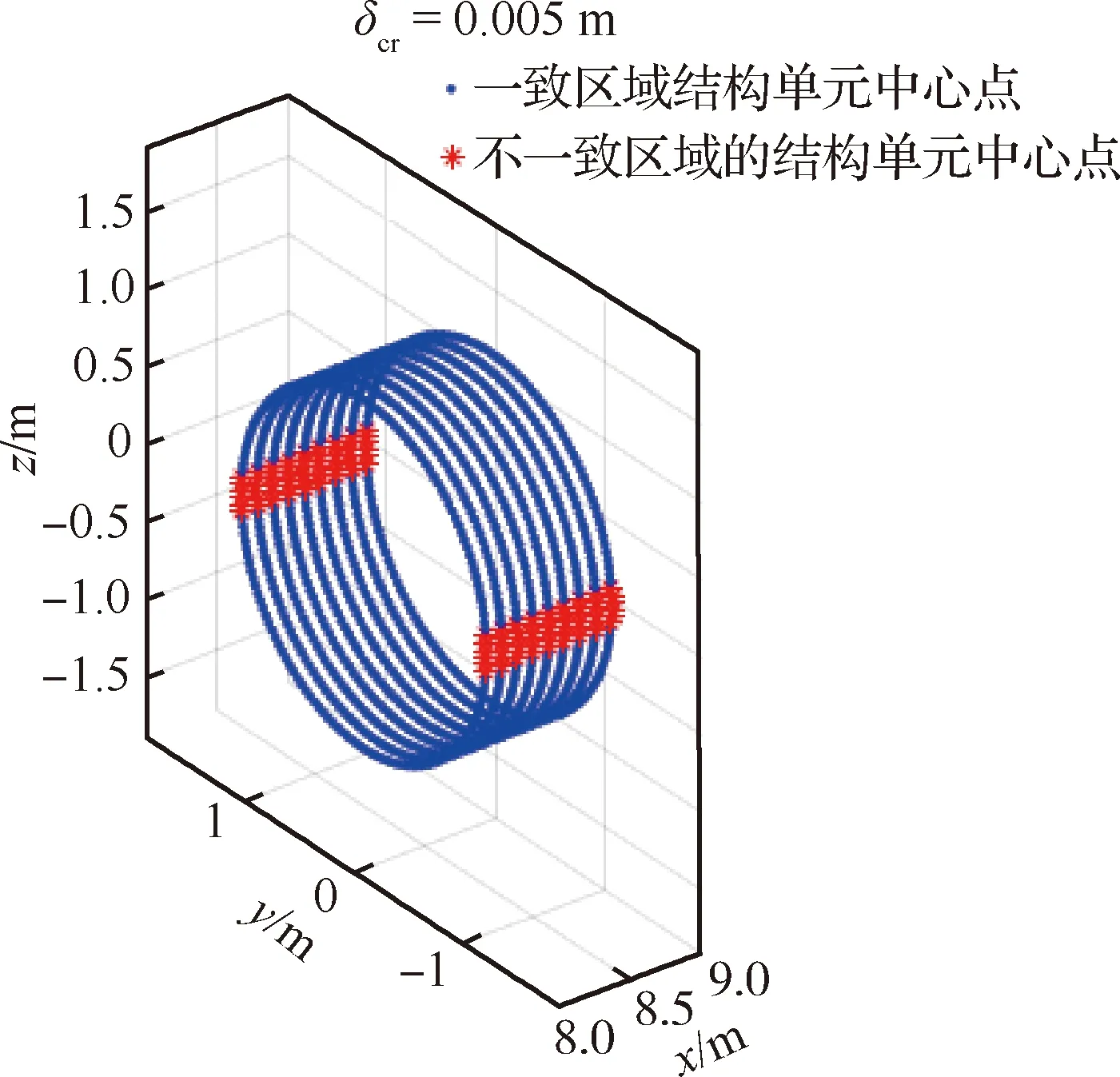
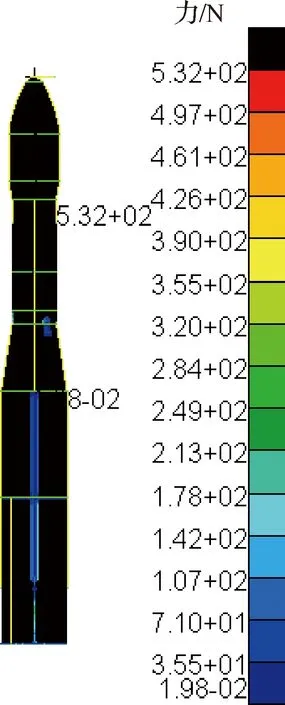
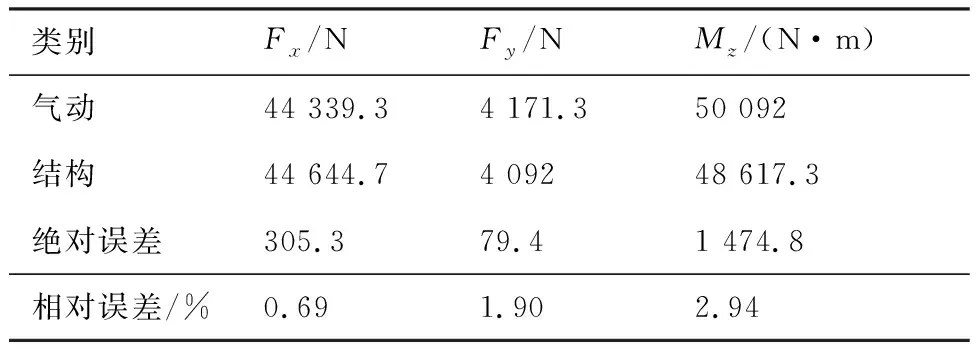
图7 气动压力点局部细节图(8 m 图8 结构单元中心点整体分布图Fig.8 Overall distribution of center points of structural elements 图9 结构单元中心点局部细节图(8 m 压力插值是在气动压力点与结构单元中心点之间进行转换,因此可直接使用TPS法转换外形一致区域的气动力,图10为外形一致区域的结构单元压力云图。而力等效法是在气动压力点与结构网格节点之间进行转换,所以要先获取3 211个结构单元的节点,共4 201个,再使用力等效法将气动压力点载荷转换到这些结构网格节点上,所得力的云图如图11所示。 最后对比载荷转换前后整体的合力和合力矩,如表1所示,各误差均小于3%,其中最严重的轴向载荷误差小于1%。该算例的计算结果表明,该方法可实现表面有凸起物的火箭的三维气动载荷直接向三维结构模型的等效转换,并且能够满足工程上的精度要求。 图10 一致区域施加的压力载荷分布Fig.10 Distribution of pressure loads in consistent areas 图11 不一致区域施加的节点力载荷分布Fig.11 Nodal force load distribution applied in inconsistent areas 表1 混合法所得合力、合力矩的误差 针对在运载火箭结构载荷精细化计算过程中遇到的气动模型与结构模型外形不匹配的问题,本文提出了一种基于压力插值法和力等效法的混合法,该混合法能自动识别出流体模型和结构模型外表面是否一致,从而针对不同的区域采用不同的方法进行载荷转换。 本方法适用于运载火箭或导弹三维有限元模型的流固载荷转换,并且具有转换精度高、转换过程自动化、工程适用性好的特点。 本文中选取了TPS法作为压力插值方法,实际上也可采用径向基函数法等其他方法,选择不同的方法可以得到不同的转换精度。此外,判断气动压力点是否在结构模型表面时所用临界值目前是人为设置的,该值会影响一致和不一致区域的划分,进而影响载荷转换精度,其自动确定方法也有待进一步研究。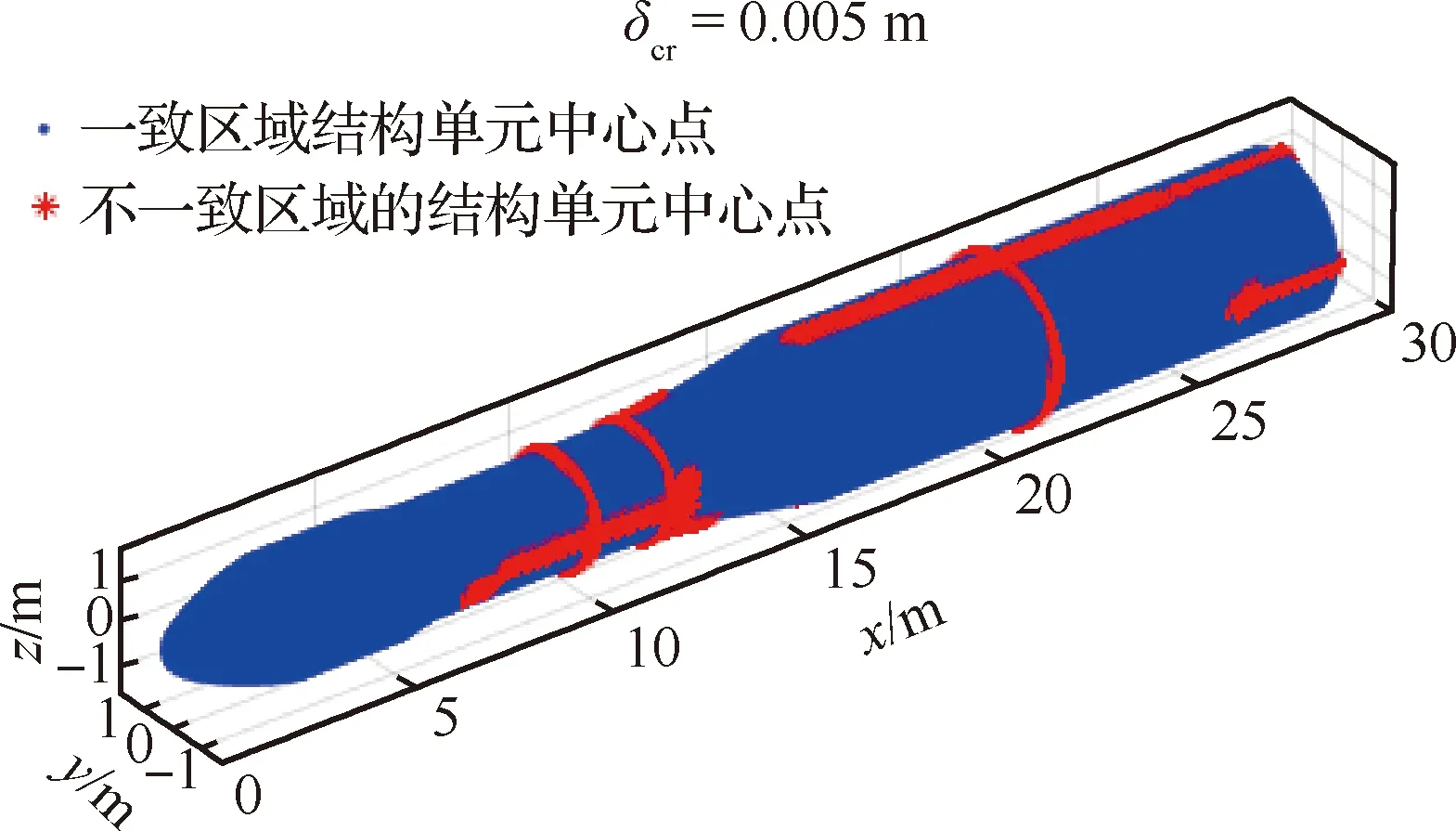
4 结 论
