应用维数分裂方法推广MUSCL和WENO格式的若干问题
2022-04-26刘君韩芳魏雁昕
刘君,韩芳,魏雁昕
大连理工大学 航天航空学院,大连 116024
2019年,在国家数值风洞工程基础研究课题的支持下,作者与国内研究高超声速边界层转捩问题的专家学者合作开展激波装配法在边界层转捩感受性问题中的应用研究,期望利用装配法消除采用捕捉法数值模拟感受性问题时在激波附近出现的虚假数值噪声,以发展全场一致的高精度数值算法。
为分析数值噪声产生的机理,选择应用广泛的五阶WENO格式作为高精度格式在有限差分框架下进行数值实验。在对数值实验结果进行分析时,发现在流场中除了激波过渡区容易出现非物理振荡外,高精度格式也可能放大因坐标变换而引起的几何诱导误差,至少在给出的曲线坐标系下的均匀流算例中,五阶WENO格式模拟的流场参数误差大于一阶迎风格式的数值模拟结果。文献调研发现,在曲线坐标系下的WENO格式确实存在会产生几何诱导误差的问题,需要构造与之相对应的消除算法,文献[8-9]的算例也验证了这一观点。几何诱导误差问题属于几何守恒律(Geometric Conservation Law,GCL)研究领域,有几何诱导误差产生即证明算法不满足几何守恒律。但是,本文作者于2020年1月参加“第二届计算流体力学中高精度方法及其应用研讨会”提出这一观点时却受到了质疑,“定性分析,构造WENO格式时使用的是积分运算,模板作用于控制体内物理量的均值,计算又是从守恒型Euler方程出发,怎么会不守恒?”
根据针对对象的不同,几何守恒律又可分为体积守恒律和面积守恒律,体积守恒律对应于运动及变形网格,面积守恒律对应于静止网格,本文所讨论问题皆基于静止网格。在有限体积法(Finite Volume Method,FVM)中,与网格相关的几何参数可以精确地求得,几何守恒律自动满足,而有限差分法(Finite Difference Method,FDM)则存在几何守恒律不能得到满足的情况。因此,关于WENO格式守恒性的讨论也可以变成对WENO格式是否属于有限体积法的讨论。“WENO格式是否属于有限体积法”是本文提出的第1个问题。
由于国内外计算流体力学(CFD)相关文献及教材对FVM的定义不同,因此本文讨论的特指对控制体采用高斯公式将体积分转换成面积通量积分的有限体积法,可称为“高斯积分型有限体积法”,为表述方便,以G-FVM表示。早期国内教材认为G-FVM和FDM存在明显差异,“对于较均匀的网格,如果坐标变换函数的计算能具有高精度,那么有限差分法可以通过多点格式或紧致格式获得高精度,但对于有限体积法很难获得二阶以上精度”。后来的教材采用了国外文献观点,认为“有限差分法和有限体积法的不同主要是对网格的几何处理方法不同,二者没有本质区别”;“在一般曲线坐标系中,对几何度量系数做适当处理后,守恒型流动方程组有限差分算法和物理空间里有限体积算法是等价的”。综合以上观点,在回答WENO格式是否属于有限体积法之前,需要先弄清楚第2个问题:G-FVM和FDM是否等价?
在数值实验及结果分析中发现从一维Euler方程出发介绍WENO格式时,如果模板作用于对流项通量,即便在非均匀网格上也不存在GCL问题。但是对于多维空间,即使是均匀正方形网格也会出现与几何参数相关的均值计算问题。由于WENO格式模板函数比较复杂,推导过程选择形式较为简单的MUSCL格式。
最早构造MUSCL格式时采用“Specific Volume”来体现网格的非均匀特性,但是国内CFD教材在介绍MUSCL格式时大部分采用直角坐标系下的均匀网格,这种情况下几何度量没有变化,“限制器的变量可以是守恒变量、原始变量、通量、特征变量等,但限制器的函数都是相同的”。即使空间一维,在非均匀网格上插值也要考虑距离的影响,定性分析空间多维曲线坐标系下的方程表达式,守恒变量和对流项通量中的几何度量系数存在量纲上的差异,由此引出第3个问题:如何使MUSCL格式和WENO格式守恒?
1 G-FVM和FDM是否等价
首先给出FDM和G-FVM的控制方程,FDM的控制方程在笛卡尔坐标系(,,,)下得到,以三维守恒型Euler方程为例:
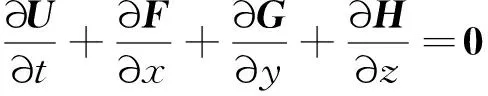
(1)
式中:为守恒变量;、、分别为、、方向的对流通量,其表达式为
=[,,,,]
=[,+,,,(+)]
=[,,+,,(+)]
=[,,,+,(+)]
其中:为密度;、、分别为、、方向的速度;为压力;为单位质量流体的总能,其计算式为
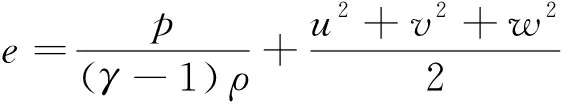
在计算具有复杂边界或外形的流场时,需要将控制方程由物理空间(,,,)变换到计算空间(,,,),变换后的守恒型控制方程为

(2)
当网格静止时,
=

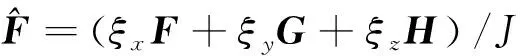
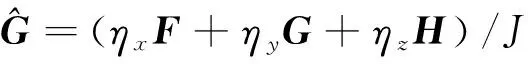

式中:为Jacobian行列式,有
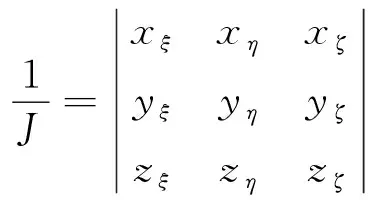
、、、、、、、、为度量系数,可通过以下公式求得:
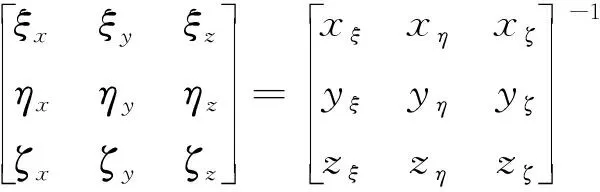
与FDM不同,G-FVM可以在曲线坐标系下直接应用,采用高斯公式把体积分变成面积分:
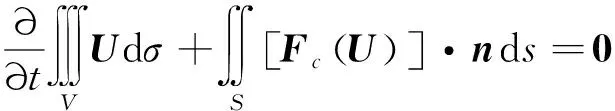
(3)
式中:是控制体体积;是控制体外表面;d表示微元体积;d表示外表面微元面积;=++表示外表面微元外法向单位矢量。对流项通量积分的函数可写为
()=++
(4)
为便于几何表达和简洁符号,采用图1所示二维空间模型,其可看做是三维网格在方向的等值面,灰色曲线表示建立FDM的网格点,黑色曲线构成G-FVM的控制体。
文献[12-13]讨论了G-FVM和FDM的不同,这里引用其主要观点:
1) FDM的数值解是网格节点处的物理量,可以采用Taylor级数写出修正方程,从而直接得到精度、相容性等格式特性;G-FVM得到的是控制体的平均值,分析格式特性需要采用其他数学手段。
2) 即使两种方法采用数值上相同的几何度量系数,其精度也有差异,控制体和积分面的几何参数对于G-FVM是精确的,用在FDM中必然是近似,根据物理空间(,,,)变换到计算空间(,,,)上的函数解析表达式计算出来的几何度量系数不能直接用于G-FVM。
3) G-FVM保持守恒性。对于均匀流动参数,采用各种精度的格式和任意形状的网格,围成封闭控制体所有面的通量积分之和为0,自动满足GCL。
除此之外,本文进一步补充如下论据:
4) FDM不需要封闭的控制体或积分面(对封闭性的理解见附录A)。在实际CFD数值模拟中,一般需要先通过CAD实体模型生成物面网格,进而形成流场计算所需的空间网格。对G-FVM来说,要求控制体的每个积分面满足封闭性,否则无法进行积分计算。例如,对图2所示物体表面存在细缝的情况,便需要通过几何修形将细缝“抹平”。而课题组近期研究工作表明FDM本质上不需要表面网格,只要找到物面点的位置信息就可以进行计算,不需要关心不同物面网格点之间的关系。
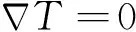
对于二阶精度的G-FVM,控制体梯度是利用相邻网格点参数重构出来的,不能保证为0,难以满足绝热壁条件。根据格心值和格心到壁面矢量重构得到的壁面温度分布不是常数,最多只能在一个点满足等温壁条件。
6) 高斯公式只能用到空间二维,把面积分转换成线积分进行计算,在空间一维中无法使用,因此,G-FVM不能退化到空间一维。
通过以上论述可知:G-FVM和FDM存在本质差异。

图1 二维曲线网格Fig.1 Two-dimensional curvilinear grid
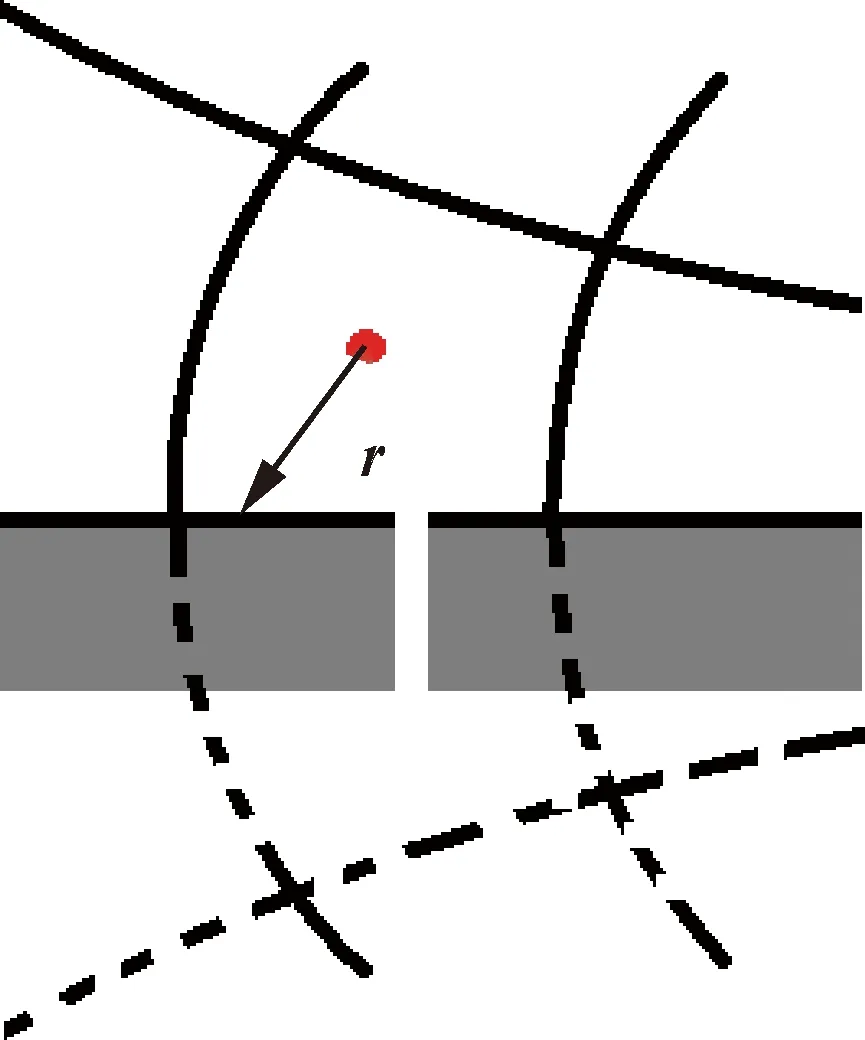
图2 物面附近网格示意图Fig.2 Schematic diagram of grid near surface
2 MUSCL和WENO格式是否属于G-FVM
按照G-FVM和FDM的特点,本文认为MUSCL类和WENO格式不属于G-FVM,下面通过G-FVM界面通量计算过程提供更多的论据。
以图3所示直角网格为研究对象,其中阴影部分为控制体,其流场参数的平均值为
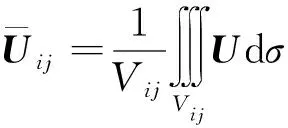
(5)

图3 均匀直角网格Fig.3 Uniform rectangular grid
应用高斯公式后通量积分变成围绕控制体的线积分,以图3中红色线段-12,为例,法向矢量=-,对流项通量为
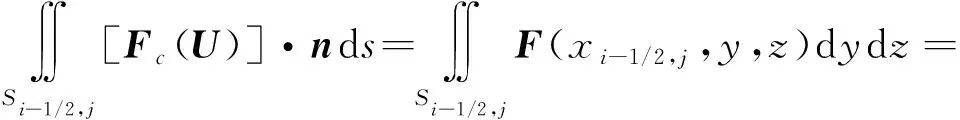

(6)
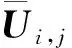
目前看到MUSCL和WENO格式的构造过程中只有线积分,从一维Euler方程出发,在半点界面处通量的通用形式为

(7)
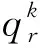
如果采用MUSCL和WENO格式计算式(6) 中G-FVM的界面通量,有两种途径:
1) 沿着方向,在参数重构中套用格式,因为在格式构造过程中没有考虑方向的变化,严格的说计算模板式(7)中的整点通量时,平均值应该采用式(8)计算:

(8)
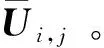
2) 同样沿着方向的积分中使用格式,计算整点通量也只能采用储存在-12,面心处的平均值:
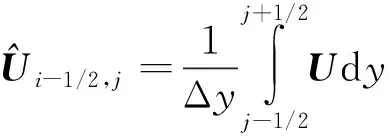
(9)

以上是在控制体左右界面的计算过程,对于上下界面还应有重新定义的平均值。通过以上分析可知:尽管式(8)和式(9)的界面都在-12,处,形式相似,但是数学本质不同:在MUSCL和WENO格式中,-12,是自变量的当地取值,在G-FVM中,-12,是参数,积分函数的自变量是d。这种数学差异导致MUSCL和WENO格式用于计算G-FVM界面通量均不够严谨。
Roe格式计算界面通量也使用了平均概念,最近Roe在文献[19]中也提到这一格式不属于FVM。因此,基于平均值构造的格式不能简单的归类于FVM。这类格式不能像FDM那样直接采用Taylor级数分析,属于FDM也不合适。MUSCL格式的原始文献采用“守恒差分格式(Conservative Difference Scheme)”和“积分格式(Integration Scheme)”表示,本文认为“积分格式”这一定义更能准确反映这类格式的特点。

图4 非结构网格中边界面通量计算示意图Fig.4 Schematic diagram of boundary surface flux calculation in unstructured grid
在非结构网格中应用MUSCL类格式,如图4 所示,在已知格心位置的守恒变量和梯度后,计算边界面通量时采用式(10)计算边界面上的守恒变量平均值L、R:
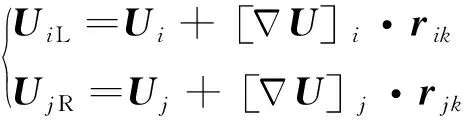
(10)
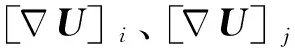
3 如何让MUSCL和WENO格式守恒
目前大部分高精度格式建立在均匀结构网格基础上,其中的模板函数公式在非均匀条件下需要增加几何权系数进行修正,以四阶中心差分格式为例进行说明。
在空间一维均匀网格上,方向导数对应的差分格式为
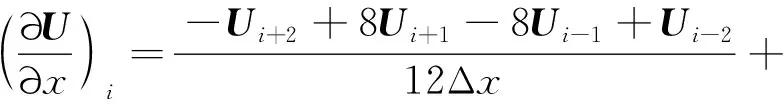
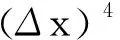
(11)
将守恒变量换成原始变量(,,)、对流项通量,式(11)同样成立,文献[16]关于限制器函数相同的结论成立。
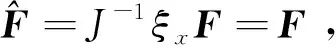
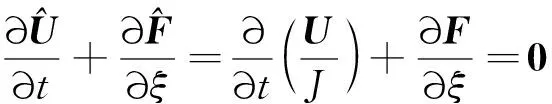
(12)
对式(12)的离散是在计算空间上进行的,理论上差分格式中的变量应该采用曲线坐标系下的相关参数。采用四阶中心差分格式离散对流通量项,得到

(13)
此时,式(13)仍保持四阶精度。但是如果采用式(11)直接离散守恒变量,得到

(14)


(15)

用GCL消除坐标变换引起的几何诱导误差,原则上不同的格式需要构建不同的GCL算法。根据相关研究文献,在高精度格式方面,SCMM(Symmetrical Conservative Metric Method)理论完善,算例验证能够消除WCNS类格式的几何诱导误差,从提供的验证算例看,借鉴SCMM构建的WENO类差分格式的GCL算法可以有效减少误差,但是误差曲线还是有明显变化。
另外一种消除几何诱导误差的算法是从离散等价方程出发应用差分格式,具体理论推导和算例验证可以参考文献[8-9],这里不再详述。
4 课题组研究成果
基于以上对G-FVM和FDM存在本质差异的认识,课题组开展如下研究,初步取得了一些成果:
1) 利用FDM不需要几何清理的特点,结合非结构网格有限差分法,建立了不生成表面网格就能进行流场计算的“扎染算法”,如图5所示。传统的笛卡尔有限体积法需要物面网格,即关联点和点形成通量积分,如果有微小缝隙就无法计算,但是FDM本身不关心点和点之间的关系,只要寻找实体模型表面点就能计算。
2) 认识到G-FVM构造高精度边界算法的困难。除了对现有边界算法进行改进外,本文课题组还在研究直接在边界点求解控制方程的全场统一算法,如图6所示。把无滑移物面条件=0(物面法向速度为0)作为约束加入到控制方程中,利用非结构网格有限差分法直接计算物面网格点参数,而传统CFD的内点计算只能计算
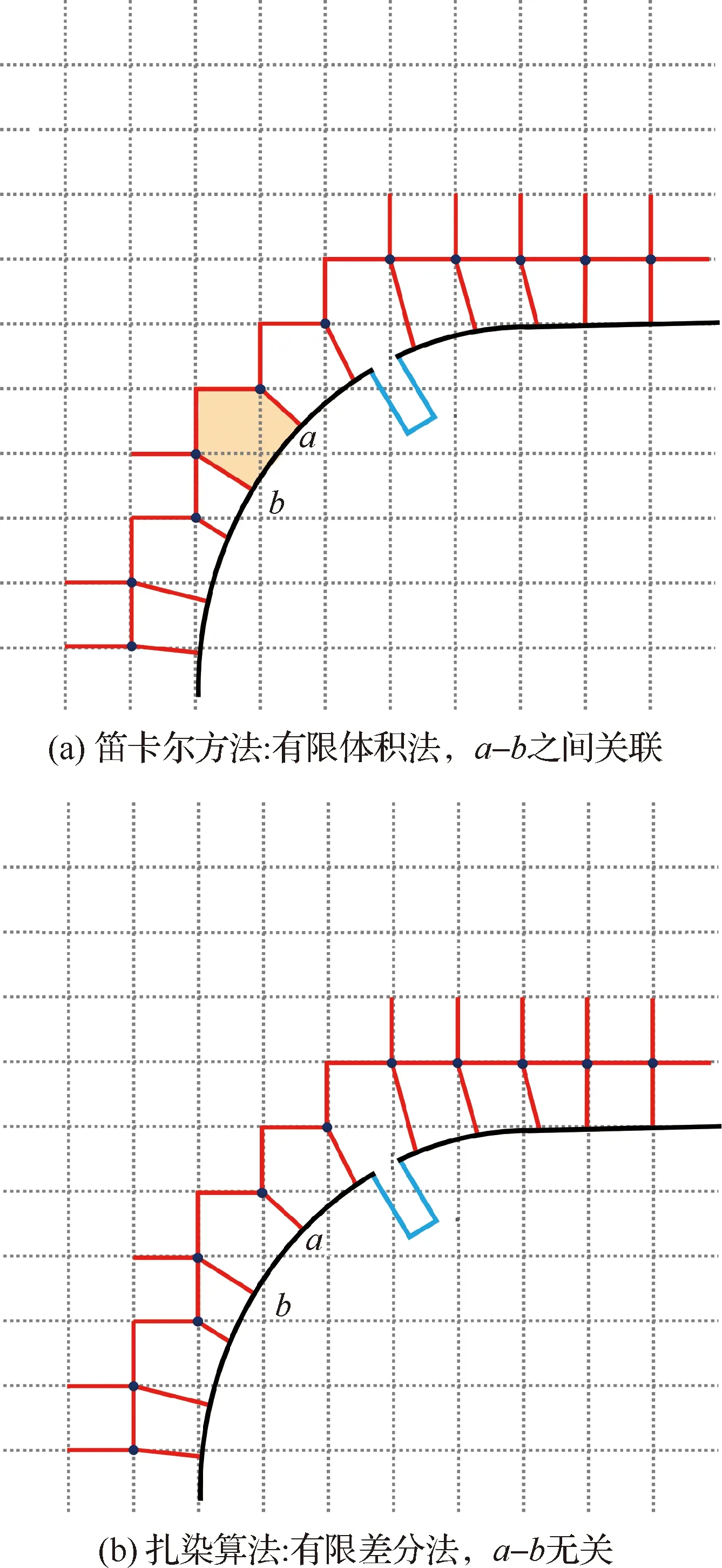
图5 扎染算法示意图Fig.5 Schematic diagram for tie-dye algorithm

图6 全场统一求解算法示意图Fig.6 Schematic diagram of whole-field unified algorithm
到第2层网格,需采用边界条件假设得到物面参数。图7为分别采用两种方法模拟Prandtl-Myer流动得到的物面附近密度等值线图,可以看出,全场统一求解算法的等值线更加光滑,定性分析更为合理。
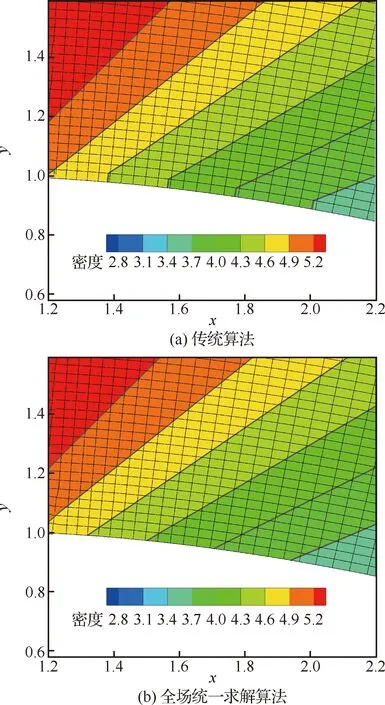
图7 不同方法得到的密度等值线Fig.7 Density contours for different methods
5 结 论
本文以3个问题为出发点,在对问题进行分析和讨论的过程中得出以下结论:
1) 有限差分法和高斯积分型有限体积法在网格需求方面存在差异。有限差分法计算不需要封闭的控制体或积分面,而高斯积分型有限体积法无法在不封闭的控制体上进行积分运算。
2) 有限差分法和高斯积分型有限体积法在边界条件处理方面存在差异。有限差分法在网格点上进行离散求解,第一类边界条件可以准确地添加到计算表达式中。高斯积分型有限体积法建立在多个积分面围成的控制体上,尽管在通量积分中可以严格满足第一类边界条件,但是梯度重构等计算过程会导致数值解不能满足施加边界条件的现象。
3) 与在多维非结构网格上直接构造的WENO格式不同,结构网格上的MUSCL格式和WENO格式存在应用于空间多维时出现的平均值多定义问题,不属于高斯积分型有限体积法。
4) 结构网格上的MUSCL格式和WENO格式不守恒。
致 谢
作者在构思过程中多次向南京航空航天大学朱君和中国空气动力研究与发展中心朱华君请教WENO格式方面的问题,在此表示感谢。
