GBM快速轨道产品及非差模糊度固定对其精度的改进

邓志国，王君刚,2，葛茂荣，3

1.德国地学中心大地测量，德国 波茨坦14473; 2.中国科学院上海天文台，上海 200030; 3.柏林工业大学，德国 柏林10553

GNSS在实时定位、导航、授时领域有重要的应用，也是对地观测的重要工具和地球监测的重要手段，在地表形变监测[1-2]、大气反演[3-4]、空间天气监测[5]等领域有着广泛的应用。精密卫星轨道钟差产品是GNSS服务的基础，是高精度GNSS应用的前提。也是用户获取国际大地参考框架(international terrestrial reference frame，ITRF)[6]的主要技术手段。

国际GNSS服务中心负责提供高精度的GNSS产品，为大地测量学和地球动力学服务[7]。其产品包括卫星轨道钟差、测站坐标、地球定向参数(Earth rotation parameters，ERP)、对流层延迟、电离层延迟等。IGS的数据分析中心包括欧洲定轨中心(CODE)、美国喷气动力实验室(JPL)、中国武汉大学(WHU)等，不同分析中心提供独立解算的产品，IGS对不同分析中心的产品进行综合处理生成IGS的官方产品。IGS及分析中心的产品主要有事后产品、(超)快速产品、实时产品等。德国地学中心(GFZ)作为IGS分析中心之一，提供高精度后处理的GPS和GLONASS轨道钟差产品(GFZ产品)[8]，以及多系统快速产品，即GBM(GFZ BeiDou multi-GNSS)产品。GBM产品从2014年开始提供快速精密轨道钟差，最初包含BDS-2和GPS卫星，在后期的完善中逐步加入了GLONASS、Galileo、QZSS和BDS-3，成为IGS分析中心中最为完备的多系统轨道钟差产品。GBM产品基于IGS全球观测站的24 h弧段数据进行处理，提供轨道、钟差、ERP和测站坐标等[9-10]。

GNSS数据处理的基本观测值是伪距和相位，高精度的相位观测值是GNSS高精度产品的保证，而模糊度固定技术能够显著提高产品解算精度。在GNSS的网解中，常用的模糊度固定方法是基于双差观测值或者双差模糊度[11-13]，即双差模糊度固定(double-differenced ambiguity fixing)。为提高精密单点定位技术(precise point positioning，PPP)[14]的精度和收敛速度，可以通过估计卫星端模糊度小数部分(uncalibrated phase delay，UPD)并播发给用户实现用户端的PPP模糊度固定(PPP ambiguity resolution，PPP-AR)[15-17]。对于GNSS网，同样可以采用估计UPD的方式实现非差模糊度固定(undifferenced ambiguity fixing)。理论上，双差模糊度固定和非差模糊度固定对于GNSS网解精度应该是等价的[18]，而后者效率更高[19-20]，但研究表明，非差模糊度固定的解算精度较双差固定有一定的提高，比如采用相同测站的非差模糊度固定比双差固定的轨道精度有10%的改善[19]，非差模糊度固定相比传统的独立双差模糊度固定对测站坐标的重复率有5%的提高[21]。对于非差模糊度固定表现好于双差模糊度固定的理解，文献[19]认为非差模糊度能够把不同弧段的模糊度连接起来，减少了自由度从而改善解的强度；文献[21]认为双差模糊度固定存在部分错误固定的模糊度，这些模糊度在非差的时候能够被正确地固定，而且剔除这些错误的固定后双差固定解的精度与非差固定解的精度相当。

本文给出了GBM快速产品的数据处理流程与策略，着重介绍了GBM产品非差模糊度固定的方法策略。分析了2015—2021年GBM轨道产品的精度，包括GPS卫星轨道与IGS最终产品的比较结果，多系统轨道的6 h预报精度，以及卫星激光测距(satellite laser ranging，SLR)的外符合精度验证。针对GBM产品2021年处理策略的升级，即采用非差模糊度固定取代双差模糊度固定，本文详细分析了轨道产品精度的相应改善。

1 GBM多系统解算模型与策略

1.1 多系统GNSS数据处理模型

(1)

(2)

式中，xs为卫星信号发射端在GCRS中的位置；xr为地面信号接收端在国际地球参考系统(international terrestrial reference system，ITRS)中的位置；Rt2c为GCRS与ITRS之间的转换矩阵。在时刻t信号在卫星发射端的位置xs(t)为

(3)

在精密定轨中，地面接收机的位置先验坐标通常是由IGS参考框架给出参考历元的坐标和速度。IGS参考框架是ITRF在GNSS技术中的实现，主要是在ITRF测站坐标上修正了接收机天线引起的系统性偏差。地面信号接收端在时刻t的位置xr(t)在ITRS可以表达为

xr(t)=xr,0+vr,0·(t-t0)+∑dx+dxr

(4)

式中，xr,0和vr,0分别为参考历元t0的测站坐标和速度；∑dx为测站的位置变化改正，主要包括固体潮、海潮、极潮、海洋极潮、大气潮等；dxr为测站坐标的参考位置到信号接收位置的矢量，主要包括接收机端的天线相位中心偏差(PCO&PCV)及天线参考位置(antenna reference point，ARP)到测站参考位置的矢量。

式(4)给出的是地面测站在基于参考时刻位置和速度实现的参考框架中的计算方法，比如ITRF和DTRF[22]，它们给出的测站坐标是以参考历元时刻的坐标、速度及震后形变函数(post-seismic deformation，PSD)表达的。对于瞬时历元地球参考框架，比如JTRF[23]，直接给出测站坐标任意时刻的值，因此不需要进行速度修正。本文主要针对的是高精度GNSS解算，比如精密轨道钟差确定。对于定位用户，根据实际应用和精度需求，式(4)中的部分改正并不需要。

最后，由于测站坐标通常是在ITRS中定义和表达，而精密定轨中的卫星轨道需要在GCRS中表达，因此ITRS与GCRS之间需要通过矩阵Rt2c进行转换，该矩阵主要包括岁差、章动、极移和地球自转改正对应的矩阵构成，在精密定轨中，需要求得该矩阵对极移(polar motion)和日长变化(length of day)的偏导，从而解算地球自转参数(Earth rotation parameter，ERP，包括极移和日长变化)。对于利用精密轨道进行定位或者钟差确定的应用，由于精密轨道通常是在ITRS给出，因此，不需要进行GCRS到ITRS之间的转换。

在GNSS高精度数据处理中，参数估计方法是重要的一部分。精密定轨处理通常采用事后处理模式，即整体最小二乘的批处理。经典精密定轨模型化、参数化等已有较为成熟的研究[24-26]，多系统的数据处理也有较多研究[27-29]。另一方面，虽然部分研究针对轨道高频更新需求探索了实时定轨的滤波解[30-31]，现有的大多IGS分析中心在事后、快速和超快速轨道都是采用批处理。

1.2 双差模糊度固定

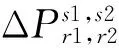
(5)

(6)

1.3 非差模糊度固定

已有研究表明接收机端和卫星端的相位硬件延迟br、bs、Br和Bs在较长时间内比较稳定，因此可以将一定时间段内的相位硬件延迟的小数部分UPD当作常数处理。在双差模糊度固定后，求解得到无电离层的非差模糊度与钟差等参数成功分离，使得UPD在网解构建成的模糊度域内具有了一致性。

(7)

式中，εWL为观测值噪音。对于一个GNSS网，使用所有卫星测站对的宽巷UPD观测值通过最小二乘方法可以解算每个测站和卫星的UPD

(8)

需要注意的是，式(8)是秩亏的，需要施加额外的基准条件进行求解。GBM产品的基准通过定义一个参考站宽巷UPD为零实现，该参考站根据观测值的可用性和质量进行择优选取。在判断宽巷模糊度的固定与否时以0.3周为阈值

(9)

现有的GNSS卫星和地面测量型接收机性能稳定，本文试验表明，GPS和Galileo卫星系统的固定率可以达到99%，BDS-2和BDS-3的宽巷模糊度固定率优于95%。

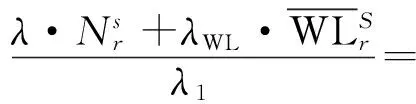
UPDNLs+UPDNLr+εNL

(10)

(11)

本文试验显示，GPS和Galileo卫星系统的窄巷模糊度固定率可以达到95%，BDS-2和BDS-3的窄巷模糊度固定率约为80%。在GBM的数据处理中，宽巷和窄巷UPD均作为单天常数进行估计。

2 试验与分析

本文介绍了GBM产品的日常处理策略与流程。GBM选用IGS核心站以及部分非核心站，根据观测值的可用性和质量，地面网会不定期进行适当调整。以2021年11月30日为例，图1给出了地面测站的分布图以及各个测站处理的GNSS系统。可以看到，虽然欧洲区域测站分布相对密集，且整体分布较为均匀，该天处理的153个测站均包括GPS观测值，对于GLONASS、Galileo、北斗及QZSS，对应的测站个数分别为149、129、98和50。除QZSS系统的测站主要分布在亚太地区外，其他系统的测站分布都比较均匀。

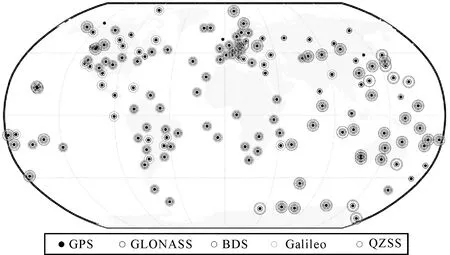
图1 GBM快速产品的地面测站分布及各测站处理的GNSS系统(以2021年11月30日为例)

图2给出了2015—2021 GBM产品包含的卫星个数。卫星个数从2015年的70颗左右，增长到2019年底的接近100颗，这段时间GPS、GLONASS和北斗卫星个数较为稳定，其中北斗主要是BDS-2的卫星，随着Galileo系统卫星的发射，GBM产品包含的Galileo卫星慢慢增加。2020年初开始，GBM产品包含BDS-3的卫星，处理的总卫星个数接近120，2020年中开始提供5系统约125颗卫星的产品。

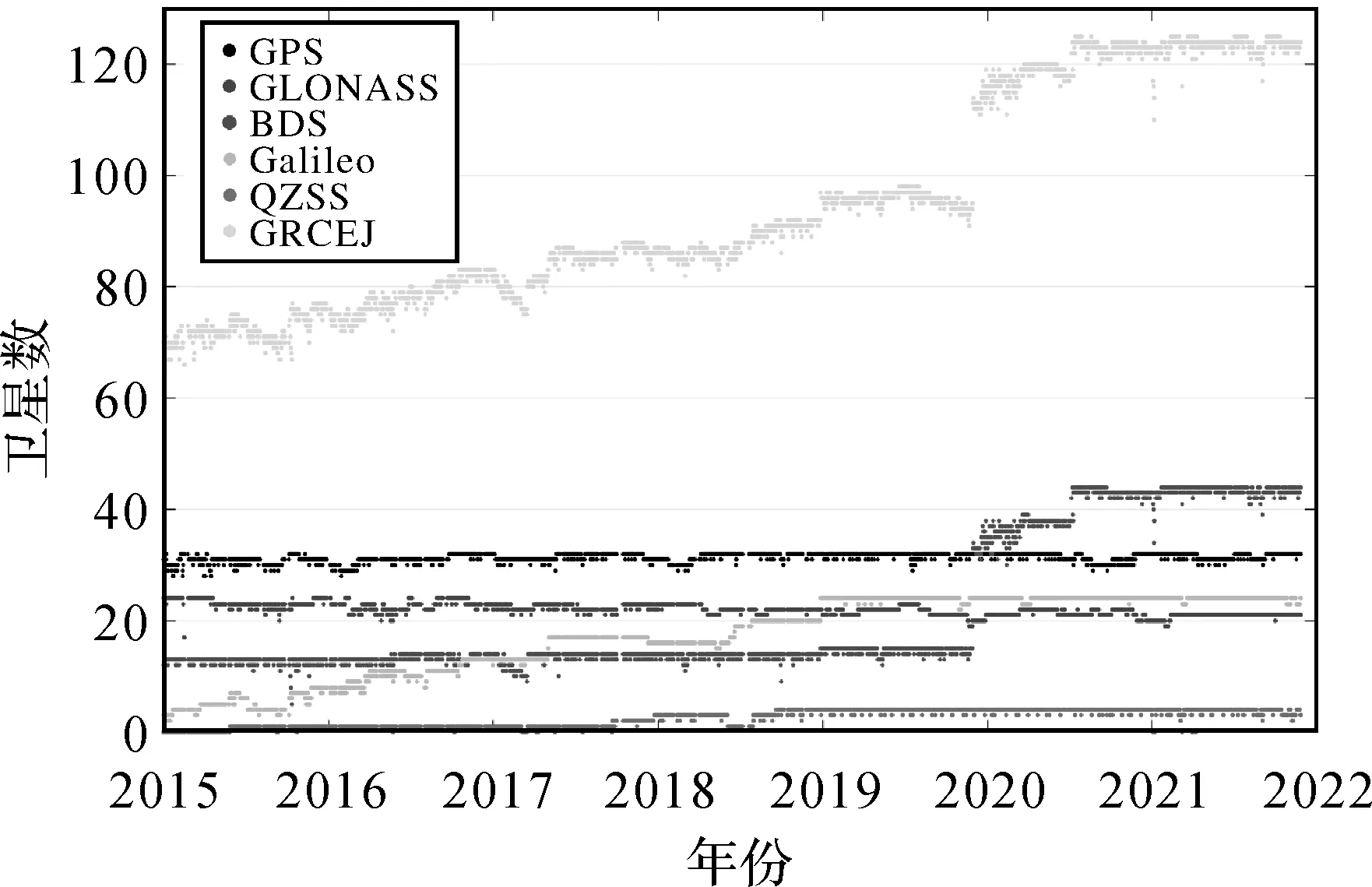
图2 2015—2021年GBM快速产品卫星个数

图3给出了GBM快速产品的处理流程，详细的数据处理策略在表1。作为IGS的日常分析中心，GBM的数据处理策略和采用的模型定期进行更新并且与IGS的数据处理标准保持一致，包括卫星光压模型、测站坐标、卫星和测站天线相位偏差等，表1展示了所采用的最新模型。GBM产品在精密定轨中采用5 min采样间隔的观测值，在轨道确定后进行钟差加密解算，此时将卫星轨道、测站坐标及模糊度参数固定，采用30 s的观测值计算卫星和接收机的钟差。

图3 GBM快速轨道钟差产品数据处理流程

表1 GBM快速产品的处理策略

对于模糊度固定，在2021年DOY 176之前采用的是双差模糊度固定，之后采用的是非差模糊度固定。需要注意的是，非差模糊度固定是在双差固定的基础上进行的，由于浮点解得到的非差模糊度与卫星和接收机钟差参数强耦合，并不直接具有可固定特性。在通过建立双差观测值消除钟差，固定双差模糊度处理后，求解得到的非差模糊度和钟差成功分离。此时的非差模糊度具有UPD整数特性，因此GBM产品先固定双差模糊度，再固定非差模糊度，从这个意义上，非差模糊度固定是传统双差模糊度固定的进一步处理。此外，模糊度固定只针对GPS、Galileo、北斗的IGSO和MEO卫星进行。GLONASS卫星由于采用了频分多址，不进行模糊度固定。

3 GBM轨道产品精度与非差模糊度的改善

GNSS卫星轨道质量可以通过内符合和外符合两种精度评估质量，其中内符合精度主要包括天边界连续性，重叠弧段吻合性及预报精度等，外符合精度主要包括其他外部产品的比较和卫星激光测距检核两种。此外，也可以通过精密定位对卫星轨道钟差产品进行质量评估。GBM的快速产品时24 h解算弧段且不存在重叠弧段，因此本文采用预报精度进行内符合精度评估。本节首先介绍GBM快速产品的轨道内符合精度，给出和IGS最终轨道比较的结果，然后通过卫星激光测距检核外符合精度，最后分析比较非差模糊度固定和双差模糊度固定对不同卫星系统的轨道精度影响。

3.1 轨道预报精度分析

首先给出轨道预报精度的分析。GBM产品的定轨弧段为24 h，将每天的轨道预报6 h后和第2天的前6 h定轨结果进行比较，计算如图4所示。

图4 预报轨道精度分析

图5给出了GBM快速轨道6 h的预报精度分析结果，包括GPS、GLONASS、Galileo及北斗的MEO和IGSO。针对每个单天定轨结果进行6 h的预报，将预报弧段与第2天的定轨结果进行比较，分别计算每颗卫星轨道残差在径向、法向、切向的均方根(root mean square，RMS)，及3个方向的均值(1D RMS)。3个分量的均值没有实际物理意义，相关统计主要是为了更好地阐述分析比较的结果。

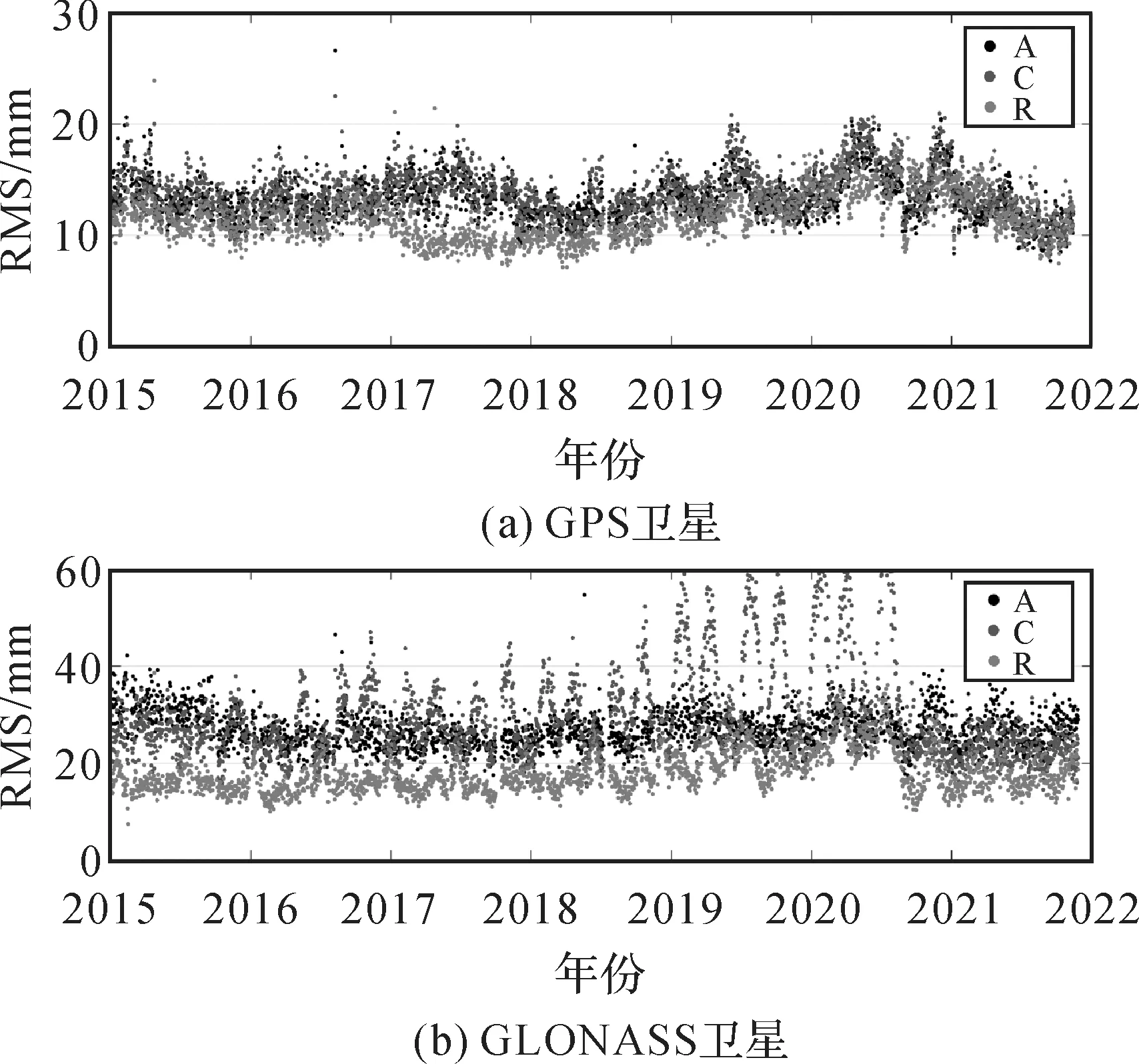
对每个GNSS系统，统计该系统所有卫星的中位数(图5)。图中每个系统在2015—2021内的均值在图例中给出。可以看出，4个系统中GPS的轨道预报精度最高，6 h的预报精度在切向、法向、径向分别为9.5、3.2、3.2 cm。Galileo和GLONASS的精度在数值统计上相当，一维RMS均值均为10～11 cm，3个分量中切向和径向精度较高，RMS值为5～6 cm。Galileo系统在2015—2016年内精度显著差于GLONASS，而2016年年底以后预报精度有了明显改善，精度提高到与GPS相当的水平，这是由于采用了BOX-WING的先验光压模型引起的。GLONASS精度相对比较稳定，但是2021年年中(模糊度固定由双差改为非差)开始可见显著改善，尤其是切向。对北斗的IGSO和MEO卫星，其精度显著差于其他3个系统，主要是由于北斗卫星系统星座复杂，其倾斜静止轨道(IGSO)卫星精度通常比中轨(MEO)卫星差，而且BDS-2卫星只有5颗IGSO和3～4颗MEO卫星，跟踪站也主要集中于亚太地区，因此定轨精度不理想。北斗系统的整体预报精度2020年初开始有着显著的提升，尤其是在径向，这是由于BDS-3卫星系统纳入解算(图2)，其MEO卫星精度显著好于BDS-2的解算精度，因此改善了整个北斗系统的统计结果。对于4个系统，轨道精度在2021年年中以后都有较为显著的改善，这是由于采用了非差模糊度固定的策略引起的，进一步的分析会在下面给出。

图5 GBM快速产品卫星轨道6 h预报精度

由于北斗系统的GEO和QZSS系统的定轨精度较差，因此将其结果单独统计(图6)。由图6可以看出，北斗GEO卫星的6 h轨道预报精度为米级，其中切向精度最差，约为3 m，径向精度约为1.5 m，法向约为0.8 m。北斗系统GEO卫星的定轨精度在2018年年底之后有显著的提升，尤其是在切向，RMS值从4 m改善到2 m以内，这是由于测站分布进行了优化。随着能够跟踪北斗卫星的测站增多，GBM根据各个测站的可用性和数据质量定期更新优化地面网。QZSS系统的6 h轨道预报精度在1.2 m左右，其中切向精度最差，约为1.7 m，法向精度最好，约为0.4 m，径向精度约为1.2 m。

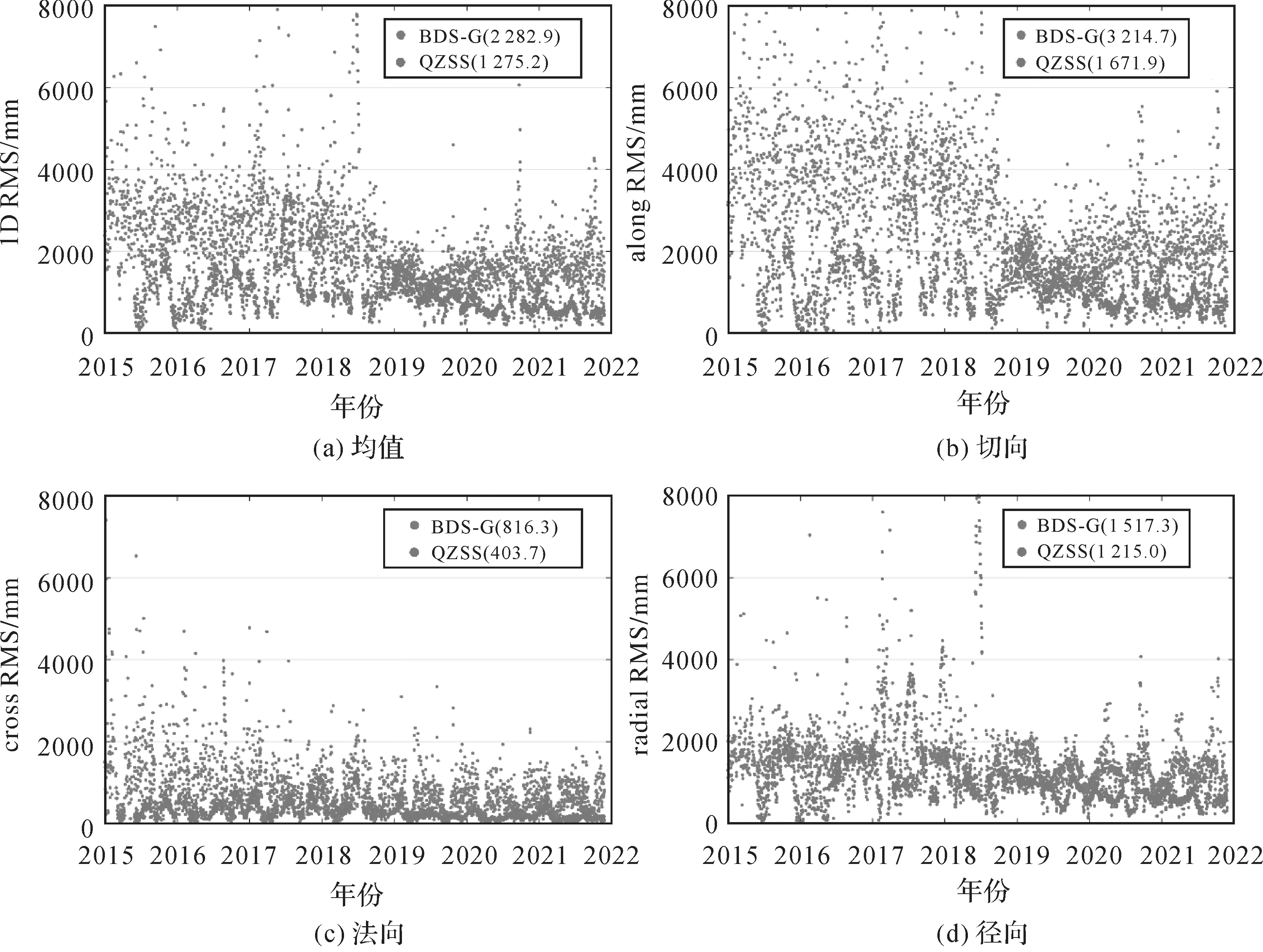
图6 GBM快速产品卫星轨道6 h预报精度

3.2 GPS卫星轨道与IGS产品比较

IGS轨道钟差综合的最终产品(final product)使用几个分析中心的最终产品作为输入，采用加权平均的方式计算得到，其精度为1～2 cm，因此比单一分析中心的最终产品有更好的可靠性和更高的精度。笔者采用IGS最终轨道产品作为参考，进一步评估GBM快速产品的GPS和GLONASS卫星轨道精度，其RMS值如图7所示。在作轨道比较的时候，对于切向、法向和径向每个分量，计算每天每个卫星轨道残差的RMS值，取所有卫星的中位数作为该天的RMS值。此外，轨道产品比较的时候不进行Helmert旋转变换。如图7所示，GBM快速产品的GPS轨道与IGS最终产品吻合度约为10～15 mm，3个分量中，径向精度最好，RMS平均值为11.7 mm，切向和法向精度略低于径向，RMS平均值分别为13.4、13.8 mm。对于GLONASS卫星，其与IGS综合轨道的吻合度显著低于GPS卫星，切向、法向、径向3个分量的RMS值分别为27、30和18 mm。

注:GPS和GLONASS纵坐标轴尺度不一样。

3.3 激光测距精度分析

卫星激光测距技术能够提供地面测站到卫星之间的高精度激光观测值，因此常用于GNSS卫星轨道的外符合精度验证。选取IGS MGEX工作组提供的2019—2021年SLR检核残差(https:∥igs.org/mgex/analysis/#slr-residuals)进行统计，结果在图8中给出。SLR统计时，对于每颗卫星，计算每天所有测站残差的均值(MEAN)和均方根误差(RMS)，对于2019—2021年期间的所有均值和均方根误差分别取均值，即为图8中的结果。由于该阶段内解算的GPS卫星未装备激光反射镜，因此没有GPS卫星的结果。对于不同卫星类型，取均值在图中给出。括号内给出该类型所有卫星的均值；其中C003为BDS-2 GEO卫星，C012为BDS-2 MEO卫星，超出上限的数字在图中给出。

图8 GBM快速轨道在2019—2021年的SLR检核结果

可以看到，Galileo FOC卫星的激光检核残差最小，所有卫星的均值为0，RMS为23 mm，而且各个卫星的精度相当，不存在特别差的卫星。对于Galileo的IOV(in-orbit validation)卫星，SLR检核结果比FOC略差，RMS值为25 mm，并且3颗IOV卫星均表现出约13 mm的系统性偏差。对于GLONASS系统，除R805卫星存在366 mm的系统偏差外，其他卫星的精度相当，所有GLONASS卫星的系统偏差(MEAN)和均方根的均值分别为16 mm和55 mm，如果扣除R805，剩余GLONASS卫星的系统偏差均值为0 mm，RMS均值为41 mm。对于北斗系统，BDS-3 MEO卫星的RMS均值为47 mm，但是4颗卫星均表现出较大的系统性偏差；BDS-2 IGSO卫星的RMS均值为47 mm，除C008外其他两颗卫星均无系统性偏差；BDS-2的MEO卫星C012呈现出-25 mm的系统性偏差，其RMS为35 mm；BDS-2的GEO卫星C003精度较差，RMS为219 mm。最后，QZSS的IGSO卫星(J001，J002，J004)RMS值为70～90 mm，均值为83 mm，GEO卫星(J003)RMS值为204 mm，所有的QZSS卫星均有较为明显的系统误差。

3.4 非差模糊度固定对卫星轨道精度的改善

从2021年年中开始，GBM产品的模糊度固定策略从双差固定切换到非差固定模式，轨道的内符合精度(即6 h的预报精度)也有着明显的改善。本小节将进一步比较非差模糊度固定对精密定轨的影响。本文选取了2021年DOY 001—DOY 150，在GBM日常处理产品(即双差固定解)的基础上，进一步进行非差模糊度固定解(处理流程如图3所示)，从而直接比较两种方法对于精密轨道的影响。由于IGS最终产品是不同分析中心的综合解，而各个分析中心现阶段都是基于双差模糊度固定，因此不再以IGS产品作为参考进行比较，只是给出轨道6 h的预报精度分析。需要强调的是，此处的双差和非差模糊度固定解采用的观测值、模型化、参数化均是严格一致的，具体处理细节参见表1，唯一的区别便是模糊度固定的方式。

图9给出了5个系统、6 h预报的卫星轨道精度，其中“DD”和”UD”分别表示双差和非差模糊度固定解。MEO卫星和GEO/IGSO卫星的轨道精度量级相差较大，由图9可以看出，对于GPS、Galileo、BDS-2和BDS-3的MEO卫星，采用非差模糊度固定都显著改善了轨道精度。对于GPS卫星，切向、法向、径向3个分量的改善率分别为12%、15%、9%，对于Galileo卫星，相应的改善率分别为13%、13%、11%，对于北斗MEO卫星、BDS-3的改善率要高于BDS-2的改善率，前者在3个分量的改善率为25%、21%、14%，后者为10%、6%、17%，究其原因，笔者认为主要是BDS-3的MEO卫星数量远大于BDS-2，模糊度固定对精度的提升更为显著，因此模糊度固定策略的升级更能提升相应的解算精度。虽然GLONASS没有进行模糊度固定，即GLONASS的数据处理策略完全相同，GLONASS卫星轨道预报精度有显著改善，在切向、法向、径向的改善率分别为15%、17%、18%。GLONASS轨道精度的改善可以通过不同系统之间的公共参数来解释：由于其他系统的轨道精度得到了改善，引起地球定向参数、测站坐标、接收机钟差及大气参数精度的提高，从而间接地改善了GLONASS卫星轨道的精度。关于非差模糊度对于这些不同系统公共参数的改善，将在后续研究中做进一步的分析与验证。

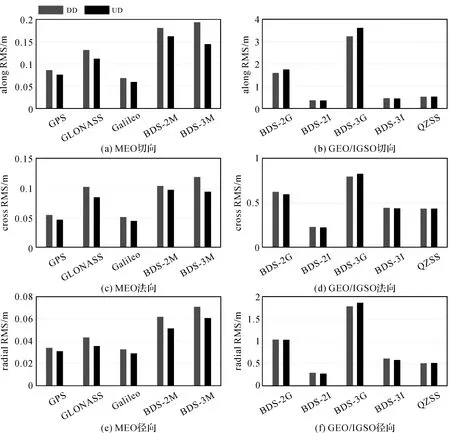
图9 GBM快速产品在2021年DOY 001—DOY 150期间轨道产品的6 h预报精度

对于北斗的IGSO和GEO卫星，以及QZSS的卫星，模糊度固定的作用相对有限。对于北斗的GEO卫星，BDS-2的精度在切向降低了10%，在法向改善了4%，在径向改善率1%，BDS-3的精度在3个方向均有降低，其中切向降低了12%，法向和径向降低了4%。由于GEO卫星的保持相对地面静止不动和轨道高度较大(36 000 km，MEO卫星约为20 000 km)的轨道特性，其地面跟踪网分布不均匀(集中在星下点附近的区域网)，卫星动力学模型不完善(缺乏足够的物理信息，以及额外的通信天线导致光压建模更加复杂)，因此GEO卫星精度一直是一个难点，现阶段的轨道精度大多在米级。另一方面，GEO并未参与到模糊度固定中，因此轨道精度的降低只能是由于公共参数等引起，详细的效果需要进一步研究。对于北斗的IGSO卫星，精度有轻微的改善，其中BDS-2卫星在切向和法向都改善了2%，在径向改善了6%，而BDS-3卫星在3个分量分别改善了4%、1%、6%。最后，QZSS卫星的精度几乎没有影响，只有在径向精度略有降低(1%)。

笔者认为，双差模糊度优于非差模糊度的原因为，在DD使用独立基线固定模糊度的情况下，双差模糊度是由同时来自2对卫星测站的4个观测值组成，这就使得双差模糊度本身在时间和空间上有了限制。而在非常模糊度固定时，是通过求解卫星和接收机端的UPD来实现的，这样就没有双差模糊度固定的时空限制，更为自由。试验数据显示，通过UD可以固定的模糊度个数比DD多大概10%，在法方程上增加的模糊度约束条件个数约30%。此外，在DD中大部分固定的双差模糊度是来自短基线，由于其时空相关性较高，对卫星轨道等全球参数误差并不敏感。非常模糊度固定可以最大程度地降低模糊度固定在时空上的相关性，提高对全球参数解算的精度。

4 结 论

本文给出了GBM快速产品的数据处理流程与策略。GBM产品采用全球分布的约150个多系统测站，处理包括GPS、GLONASS、Galileo、BDS-2、BDS-3及QZSS几个系统的数据。GBM产品传统的处理方法采用双差模糊度固定，于2021年年中采用了非差模糊度固定策略。本文分析了GBM多系统轨道产品在2015—2021年的精度。在轨道6 h预报结果的统计上，GPS卫星的精度约6 cm，其他系统为10～20 cm，其中Galileo系统2016年底开始精度提升到与GPS相当的水平。对于GPS卫星，GBM产品和IGS最终产品的吻合度在径向达到了11.7 mm，其他两个分量约为13 mm。此外，通过卫星激光测距的分析，Galileo卫星轨道精度约为23 mm，GLONASS卫星为41 mm，BDS-3的MEO卫星为47 mm。由于采用了非差模糊度固定，GPS、GLONASS、Galileo、BDS-2、BDS-3的MEO卫星定轨精度都有明显的提升，改善幅度约为9%～15%、15%～18%、11%～13%、6%～17%和14%～25%。下一步的研究将深入量化非差模糊度固定对GNSS精密定轨的影响，系统分析对其他参数的影响，并且从原理角度阐述非差模糊度固定相对双差固定的优势。