微间隙持续放电下电缆接头温度-应力分布及界面开裂规律研究

王成江，郭鸣锐，张 扬，曾洪平，张 婧，祝梦雅

（三峡大学 电气与新能源学院，湖北 宜昌 443002）

0 引言

高压电缆接头为多层固体复合介质绝缘结构，是电缆系统的薄弱环节，据统计，由接头附件造成的电缆故障约占运行总故障比例的64%[1-4]。除因生产工艺导致的缺陷外，电缆接头在现场安装过程中若出现划痕、磕碰或硅脂涂抹不均匀等不当操作，极易导致电缆绝缘材料破损和结构的不均匀发热膨胀，也会在接头附件与电缆本体交界面处形成气隙缺陷[5]。缺陷的存在会导致局部电场畸变并引发间隙放电，放电产生的局部高温和应力集中现象会加速电缆绝缘的老化，导致电缆附件的绝缘介质击穿、烧毁甚至炸裂，严重影响电网的安全运行[6-9]。

目前，有关缺陷对电缆接头电场与温度场的影响研究较多。文献[10-11]研究了多种典型缺陷对电缆接头电场强度分布的影响。文献[12-16]通过建立电热耦合模型，对缺陷电缆接头电场与温度场的分布特性进行研究。而关于缺陷对电缆接头结构损伤的研究较少，且主要集中在应力分析上。文献[17]提出了一种基于等效热源的介质管件放电热应力场的计算方法，并对电缆接头绝缘介质中出现电弧放电时的温度及热应力分布进行了研究。文献[18]研究电缆接头在不同内部缺陷下的电-热-力规律，并结合材料断裂的临界应力准则，得出导致电缆接头爆炸的阈值。文献[19]研究电缆接头在正常运行和绝缘材料中含有杂质缺陷时电场、温度场和热应力的分布规律，并对这种典型缺陷下复合材料热应力分布的二次畸变情况进行了分析。上述文献的研究重点都集中在电场、温度场上，对应力场的分析只考虑热应力，而忽略了气体压力和机械力的影响，且目前对因气隙缺陷持续放电产生的热与应力集中效应而造成的电缆接头界面开裂现象仍然缺少研究。掌握气隙持续放电下电缆接头温度、应力及界面开裂的变化规律对于进一步认识故障现象，从而指导电缆接头的制作与安装具有重要的理论意义。

本文以110 kV单芯高压电缆接头为原型，建立三维仿真模型，分析间隙等效放电功率、气隙压强、气隙厚度及气隙位置对接头温度、应力及界面开裂程度的影响。

1 电缆接头建模与计算

1.1 电缆接头模型的建立

由于目前检测设备无法实测出运行中电缆接头的应力分布情况，且间隙放电受多种因素影响具有随机性与不可控性，本文采用有限元软件，通过仿真的方式进行研究。

XLPE电缆因结构简单、质量轻、耐热好、负载能力强、耐化学腐蚀、机械强度高等优良性能而被广泛应用。本文参考YJLW03-Z64/110 kV型电缆及其预制式中间接头的结构与参数，并结合电缆接头运行中最常出现界面气隙的位置，分别在应力锥-硅橡胶界面、硅橡胶-主绝缘界面和半导电带-连接管界面3处典型位置添加界面气隙。由于气隙的形状具有随机性，为方便计算，将仿真中的气隙形状设置为环形。在电缆接头制作中，需排查界面处是否有明显缺陷，从而保证在电缆运行中复合界面处不会有较大气隙的出现，因此本文建立厚度为1～2 mm、长度为10 mm的环状微气隙，其电缆接头模型如图1所示。

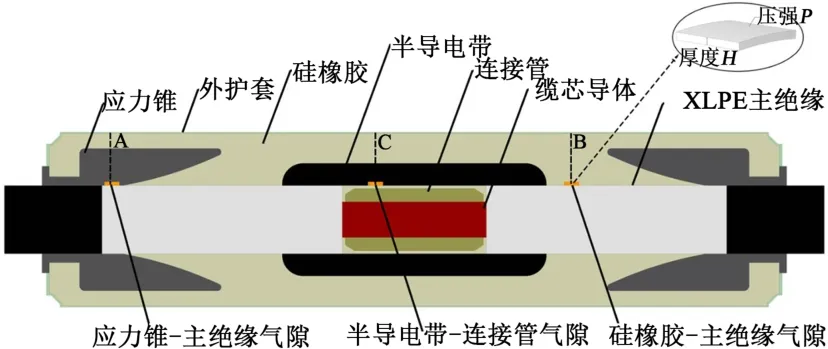
图1 电缆接头模型Fig.1 Cable joint model

1.2 计算原理

本文引入一种与放电热效应等效的热源，即间隙等效放电功率来衡量间隙放电的强弱程度。因为电缆绝缘间隙放电与介质阻挡放电（DBD）具有相似性，可以用来计算电力电缆中的放电能量[20]。

图2为工频DBD模型和等效电路。图2中，Cd1和Cd2是绝缘介质的等效电容，Cg是间隙的等效电容。因为当间隙被击穿时，间隙的电压保持稳定，所以间隙可以等效于齐纳二极管。DBD间隙的放电能量可按式（1）计算。

图2 DBD模型及其等效电路Fig.2 DBD model and equivalent circuit

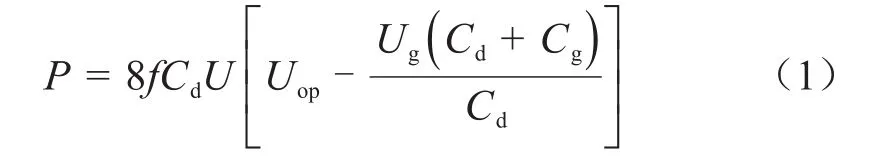
式（1）中：f是频率；Cd是绝缘介质的电容，等于Cd1和Cd2之和；Uop是电极之间电压的峰值；Ug是DBD的间隙电压。当间隙发生故障时，可通过测量外部电路的伏安特性来计算间隙电压。因为气隙位置和气隙面的粗糙程度不同，间隙电压不同，所以间隙放电能量也不同。

考虑电缆表面是通过对流与辐射的形式与外界进行换热，则电缆接头温度场的表达式如式（2）～（4）所示[21]。

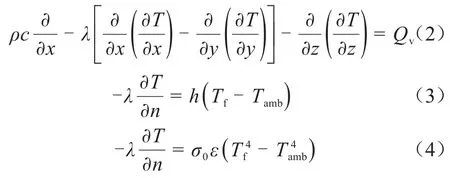
式（2）～（4）中：ρ为材料密度；c为材料比热容；T为待求温度变量；λ为材料热导率；Qv为热源密度；h为表面对流换热系数；Tf为接头表面温度；Tamb为环境温度；σ0为斯蒂芬-玻尔兹曼常数，其值为5.67×10-8；ε为表面发射率。

忽略由电磁力对应力场的影响，电缆接头结构的应力场表达式为式（5）～（9）所示。

式（5）～（9）中：ρ为材料密度；u为位移；s为应力张量；s0为应力张量初始值；Fv为体积力；ε为应变张量；ε0为应变张量初始值；εth为应力应变张量；E为弹性模量；v为泊松比；α为热膨胀系数；T和Tref分别为温度和参考温度。

假设气隙内部为理想气体，其压强可由状态方程求出，如式（10）所示。

式（10）中：P为气体压强；V为气体体积；n为气体物质的量；R为通用气体常数，其值为8.314 41 J/(mol·K)；T为气体温度，本文取参考温度为30℃。

1.3 网格剖分及边界条件设定

本文以有限元仿真软件ANSYS Workbench为研究工具，由于涉及气体与固体的热力学分析，采用Fluent模块与Mechanical模块流固耦合的方式进行仿真计算。在SpaceClaim模块中建立存在界面气隙的电缆接头三维仿真模型，通过Mesh模块对电缆接头模型进行网格剖分。为提高仿真计算准确性，使用四面体单元的非线性网格划分法，对电缆接头模型各部件交界面及气隙附近的网格进行加密处理，并假设电缆接头附件与电缆本体之间无相对滑动，设置其界面接触方式为Rough，接触算法采用Normal Lagrange法，此种方法可以将接触压力作为一个自由度来满足接触兼容性，可在最大程度上消除接触穿透，保证仿真计算准确性。为保证仿真的计算效率，在边界条件设定中，作出如下假设[22]：

（1）电缆接头各结构的材料特性参数是常数，不随温度的变化而发生变化，仿真中所用材料的物性参数如表1～2所示；

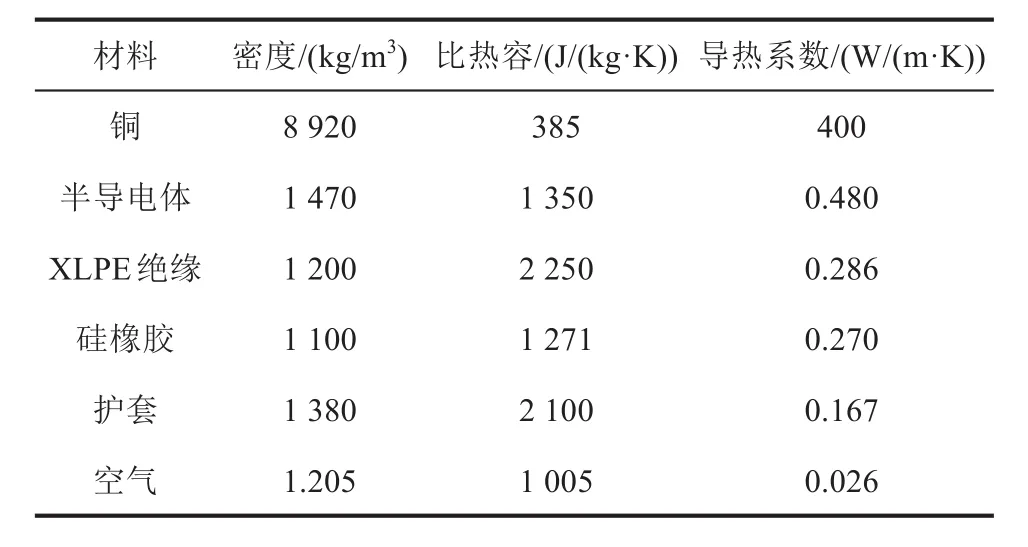
表1 用于温度场计算的材料物性参数Tab.1 Material property parameters used for temperature field calculation

表2 用于应力场计算的材料物性参数Tab.2 Material property parameters used for stress field calculation

（2）忽略接头内部金属损耗和介质损耗产生的热，认为电缆温升的原因是通电缆芯产生的焦耳热；

（3）因气隙体积微小，假设间隙放电产生的热量均匀分布在气隙内。

本文取电缆载流量为1 000 A，并将其转换为热源的形式施加于缆芯；电缆与外界的对流换热系数h为5.6 m2·K；接头表面发射率ε为0.6；外界温度为30℃；电缆接头附件与电缆XLPE主绝缘结合界面的初始面压为0.25 MPa[23]。

2 仿真结果分析

电缆接头气隙缺陷的存在使局部温度与应力场发生畸变，在高温和力的作用下绝缘材料发生不同程度的形变，导致复合界面发生开裂现象，因此研究接头温度与应力的变化规律对研究界面开裂具有指导意义。

图3为电缆接头正常运行和存在气隙且间隙放电功率为1 W，并达到热平衡时硅橡胶-主绝缘气隙缺陷电缆接头的温度与应力分布情况。

图3 电缆接头硅橡胶-主绝缘微间隙时的局部温度-应力分布Fig.3 Local temperature-stress distribution of cable joint with silicone rubber-main insulation micro-gap

从图3可以看出，当接头内部不存在气隙（正常运行）时，硅橡胶界面处温度在65℃左右，绝缘材料中应力分布均匀，最大值约为0.21 MPa。而当界面处存在间隙时，局部温度明显上升，气隙周围最高温度可达104℃，相比正常运行时升高了39℃；绝缘材料中应力分布也变得极不均匀，在间隙面处出现应力集中现象，最大应力值达到0.255 MPa，相比正常运行情况下增大了0.043 MPa。

2.1 温度变化规律分析

2.1.1 间隙等效放电功率对气隙温度的影响

保持气隙尺寸不变，气隙初始压强为0.1 MPa，3处气隙最高温度随间隙等效放电功率的变化趋势如图4所示。从图4可以看出，当间隙内不存在放电时，半导电带-连接管气隙温度最高为80.28℃，而应力锥-主绝缘气隙和硅橡胶-主绝缘气隙位置温度分别为63.31℃和68.92℃，随间隙等效放电功率的增加，气隙最高温度随之升高。其中半导电带-连接管气隙的温度升高增幅最慢；当间隙放电功率增大到5.0 W时，半导电带-连接管气隙温度升高至187.85℃；而硅橡胶-主绝缘气隙的温升速度最快，相同条件下，温度升高至378.75℃，增幅接近前者的两倍。造成这种现象的原因是连接管金属材料拥有良好的导热性能，当间隙不存在放电时，热量可通过连接管传导入气隙中，造成其初始温度高于其他气隙位置；而间隙内发生放电，温度又急剧升高时，热量又可以通过连接管传导入缆芯中，导致其温度上升较慢。气隙内间隙放电能量越大，温度越集中，局部热膨胀和不规则形变程度均会增大，使界面产生开裂现象。电缆接头若长时间处于较高的温度下，会造成绝缘介质热侵蚀，加速绝缘老化，增加电缆绝缘故障风险。

图4 气隙最高温度随间隙放电功率变化Fig.4 The maximum air gap temperature varies with the gap discharge power

2.1.2 气隙厚度对气隙温度的影响

在上述模型基础上，保持气隙初始压强为0.1 MPa，改变气隙厚度，分别记录间隙等效放电功率为0.1 W和1.0 W时，3处位置的气隙最高温度随厚度的变化规律，如图5所示。从图5可以看出，随气隙厚度的增加，3处气隙的最高温度均呈下降趋势，且间隙放电功率越大，气隙温度变化受厚度的影响也相对明显。当间隙放电功率为0.1 W时，气隙厚度由1.0 mm增加到2.0 mm，3处气隙温度变化均不超过1℃，变化幅度很小，其中应力锥-主绝缘气隙的温度变化最大，下降了0.41℃。而间隙放电功率为1.0 W时，相同条件下应力锥-主绝缘气隙最高温度由139.42℃下降到136.14℃，下降幅度为间隙放电功率0.1 W时的8倍。造成这种现象的原因是散热量与气隙表面积和温度有关，当达到热平衡时，气隙内部生热量等于散热量。放电能量一定时，气隙厚度越小，其散热面积越小，能量越集中，温度也越高。当气隙增加一定厚度，即散热面积增大时，根据热平衡条件，其间隙放电能量越大，温度变化量也越大。

图5 气隙最高温度随气隙厚度变化Fig.5 The maximum temperature of air gap varies with the air gap thickness

2.2 应力变化规律分析

2.2.1 间隙等效放电功率对接头应力的影响

保持气隙尺寸不变，气隙初始压强为0.1 MPa，考虑放电温升对气隙压力的影响，气隙面应力最大值随间隙等效放电功率变化如图6所示。

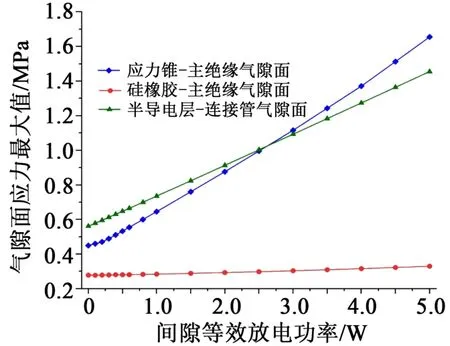
图6 气隙面最大应力随放电功率变化Fig.6 The maximum stress of the gap wall varies with the discharge power

从图6可以看出，随间隙放电功率的增加，气隙面应力最大值均呈上升趋势，其中应力锥-主绝缘气隙面应力增幅最快，当间隙放电功率增加到5.0 W时，其应力最大值为1.655 MPa。而硅橡胶-主绝缘气隙面应力最大值增大较为缓慢，相同条件下的增幅约为0.05 MPa。

造成以上现象的原因是间隙放电不仅会引起热应力的增大，也会造成气隙压强的升高，而气隙面应力是接头附件与电缆间的初始紧握力、热应力以及气隙压力共同作用的结果，热应力与气隙压力作用方向不同，二者有相互抵消的效果。电缆附件不同材料的弹性模量与热膨胀系数不同，相较于半导电材料，硅橡胶弹性模量小，热膨胀系数大，气体压力对其形变的作用效果相对明显，从而抵消部分因热膨胀产生的应力，所以硅橡胶-主绝缘气隙处应力随间隙放电能量增长速度较慢。而半导电材料的弹性模量与热膨胀系数均较大，由气体压力产生的形变效果较弱，而由温度造成的热膨胀效果较明显，使间隙放电热效应在应力增大中起主要作用，所以应力锥-主绝缘和半导电带-连接管气隙处的应力值随间隙放电功率的增加呈快速增大的趋势。由前文研究可知，间隙放电热效应会在局部产生高温，使橡胶材料的抗张强度大幅减小，在受到较大应力时更易形成微孔或裂纹，且电缆接头处于强电场作用下，带电粒子在裂纹中更容易获得加速，也会造成缺陷附近分子链断裂，加速绝缘老化[24]，甚至引起绝缘材料破裂而导致击穿事故的发生。

为观察不同间隙放电功率下接头附件应力分布的变化情况，沿图1中A、B、C路径每隔1 mm取一观测点，记录路径上的应力值并绘制于图7。

图7 不同间隙放电功率下气隙局部应力的分布Fig.7 The local stress distribution of air gap under different gap discharge power

从图7可以看出：①间隙放电对气隙局部应力分布的影响非常明显，以硅橡胶-主绝缘气隙缺陷接头为例，当气隙内不存在放电时，观测路径上的应力分布曲线呈先增大后减小的趋势，并在距离气隙8 mm处达到最大值，而随间隙放电功率的增加，气隙附近应力不断增大，最终达到检测路径上的最大值，应力分布曲线也变为单调下降趋势。②应力变化在硅橡胶材料中的衰减速度远大于半导电体材料。当间隙放电功率由0 W增加到4 W时，硅橡胶-主绝缘气隙缺陷接头的应力分布曲线在检测终点处的应力差值为0.014 MPa，而相同条件下应力锥-主绝缘气隙缺陷接头的应力曲线差值达到0.307 MPa，为前者的21.47倍。

2.2.2 气隙压强对接头应力的影响

缺陷电缆接头气隙形成的原因不同，其内部压强也存在差异。例如在接头制作时因划伤、磕碰等外力因素形成的气隙，由于受到挤压作用，气隙压强通常等于或大于标准大气压，即0.1 MPa。而由受热不均形成的气隙，由于此处本无气体，其气隙压强通常小于标准大气压。且当气隙内部发生放电时，气体温升会引起热膨胀，甚至高温对周围绝缘介质的烧蚀而产生有机蒸汽，也会使气隙压强发生改变。本文定义当气隙压强小于标准大气压时为负压，大于标准大气压时为正压。保持气隙尺寸不变，间隙等效放电功率为0.1 W，改变气隙初始压强，得到气隙面应力最大值变化曲线如图8所示。

图8 气隙面最大应力随气压变化Fig.8 The maximum stress of the gap wall varies with the air pressure

从图8可以看出，当气隙为负压时，3处气隙面的应力最大值均高于标准气压下的应力值，说明气隙负压有增大局部应力的效果。随气隙压强的增加，3处气隙面应力值均呈先减小后增大趋势；当气隙压强为0.30 MPa时，应力锥-主绝缘气隙面和硅橡胶-主绝缘气隙面的应力最大值达到最小，分别为0.326 MPa、0.072 MPa，相比气隙压强为0.10 MPa时分别下降了32.2%和73.1%；当气隙压强为0.35 MPa时，半导电层-连接管气隙面的应力最大值达到最小，为0.448 MPa，相比气隙压强为0.1 MPa时下降了42.9%。可以看出气隙压强变化对硅橡胶处应力的影响要明显高于半导电材料处。

为观察在气隙初始压强改变下应力分布的变化情况，按图7所用方法绘制图9。从图9可以看出：①当气隙压强为0.05 MPa时，3处观测路径上的应力值均高于标准气压下的值，但应力沿径向的变化趋势是一致的，证实了气隙负压对局部应力的增大作用。②气隙压强变化对硅橡胶材料处的应力分布影响要远大于半导电体材料处。以硅橡胶-主绝缘和应力锥-主绝缘气隙缺陷接头为例，当达到应力最小值所对应的气压值时，硅橡胶-主绝缘气隙附近应力值最小，应力分布曲线发生改变而趋于平缓，而应力锥-主绝缘气隙处应力分布曲线只是大小上发生变化（注：电缆接头中的应力锥为半导体材料）。③与图7对比可得，气隙压强引起的应力变化曲线在检测路径终点处的差值较小，而间隙放电引起的应力变化曲线在检测路径终点处依然有较大差值，所以相比于气隙压强改变，间隙放电对电缆接头应力畸变的影响范围更大。

图9 不同气隙压强下局部应力分布Fig.9 The local stress distribution under different air gap pressures

2.2.3 气隙厚度对应力的影响

保持气隙初始压强为0.1 MPa，改变气隙厚度，分别记录间隙放电功率为0.1 W和1.0 W时，气隙面应力最大值的变化情况，如图10所示。从图10可以看出，当间隙放电功率为0.1 W时，气隙面应力最大值随气隙厚度的增加呈增大趋势，其中应力锥-主绝缘气隙面的应力增幅最大，气隙厚度由1.0 mm增加到2.0 mm，其应力最大值由0.443 MPa增大到0.468 MPa，增幅为0.025 MPa。而间隙放电功率为1.0 W时，气隙面应力最大值随气隙厚度的增加呈减小趋势，以应力锥-主绝缘气隙为例，相同条件下其应力最大值由0.675 MPa减小到0.639 MPa，变化量为0.036 MPa。这是因为间隙放电功率较小时，改变气隙厚度对温度的影响很小，可以推断在小间隙放电能量时，厚度增加导致形变量增大是气隙面应力增大的主要原因。而间隙放电功率较大时，随气隙厚度的增加，气隙温度变化较为明显，成为应力增大的主要因素。

图10 气隙面最大应力随气隙厚度的变化Fig.10 The maximum stress of the gap wall varies with air gap thickness

2.3 界面开裂规律分析

由前文研究可知，气隙缺陷内发生持续放电会引起局部温度及应力集中现象，导致绝缘材料发生不同程度的形变，使接头复合界面出现开裂现象，从而使电缆接头的电-热-应力场发生二次畸变，可能引发更严重的放电现象和绝缘事故。

为探究间隙放电功率和气隙压强对电缆接头界面开裂的影响，定义电缆接头的界面开裂量为复合界面上绝缘材料远离界面法向的位移值，界面收缩量为靠近界面法向的位移值。由于XLPE材料弹性模量很大且热膨胀系数小，可以忽略其形变效果而只研究硅橡胶和半导体材料的位移变化。保持气隙厚度为2 mm，气隙初始压强为0.1 MPa，得到接头界面开裂量随间隙放电功率的变化如图11所示。保持气隙厚度为2 mm，间隙放电功率为0.1 W，得到接头界面开裂量随气隙压强的变化如图12所示。

图11 间隙放电功率对界面开裂的影响Fig.11 The effect of gap discharge power on the interface cracking

图12 气隙压强对界面开裂的影响Fig.12 The effect of air gap pressure on the interface cracking

由图11可以看出：①随间隙放电功率的增加，气隙厚度呈收缩趋势，且收缩量逐渐增大。这是因为绝缘材料因热膨胀产生的收缩形变效果要大于气隙压强增大而产生的膨胀形变效果，且热膨胀始终朝向靠近界面的方向，因此当间隙放电功率增加时，气隙呈收缩趋势。其中硅橡胶-主绝缘气隙随放电功率增大而收缩的速度最快，当间隙放电功率为1.0 W时，缺陷处界面的最大收缩量为0.826 mm，达到缺陷初始厚度的43.1%，而间隙放电功率达到4.0 W时，气隙缺陷处最大收缩量已达到2 mm。②电缆接头发生间隙放电后，会在距原气隙一段距离发生界面开裂现象，即界面处的绝缘材料产生远离界面的位移，这会导致新气隙的出现。新气隙的位置和大小与原气隙的材料相关，相同条件下硅橡胶材料处产生的新气隙厚度更大，与原气隙的距离更远。且随间隙放电功率的增加，接头界面的开裂程度也逐渐增大。以硅橡胶-主绝缘气隙界面为例，因间隙放电产生的新气隙出现在距原气隙位置约50 mm处，且关于原气隙呈左右对称。当间隙放电功率为1.0 W时，新气隙的厚度最大值约为原气隙厚度的6.4%，放电功率为5.0 W时，新气隙厚度达到原气隙厚度的12.25%，相比前者增大近一倍。而对于半导电带-连接管气隙界面，新气隙出现在距原气隙约50 mm处。当放电功率为5.0 W时，新气隙厚度最大值为原气隙厚度的7.1%，远小于相同条件下硅橡胶材料处产生的新气隙厚度。造成这种现象的原因是间隙放电功率越大，温度和应力的集中效果越明显，绝缘材料的不规则形变程度越大，而硅橡胶材料的弹性模量要远小于半导电材料，受到相同应力作用下其形变量更大，因此界面开裂现象更明显。

由图12可以看出：①气隙负压使气隙呈收缩的趋势，并在原气隙一段距离处产生新气隙。以硅橡胶-主绝缘气隙界面为例，当气隙初始压强为0.05 MPa时，原气隙的最大收缩量为0.976 mm，相较于标准气压时厚度减小了72.9%，且在距原有气隙约10 mm处有新气隙产生，最大厚度约为原气隙的18.8%。②当气隙压强大于标准大气压时，原气隙呈扩张趋势，并导致缺陷两侧的界面出现开裂现象，且随气隙压强升高，界面开裂量逐渐增大，引起原气隙的不断扩张。同样以硅橡胶-主绝缘气隙缺陷界面为例，当气隙压强为标准大气压时，气隙处界面的最大收缩量为0.564 mm，气隙两侧界面无明显开裂现象，而气隙初始压强为0.5 MPa时，缺陷处界面的最大扩张量为1.529 mm，达到缺陷初始厚度的76.45%，缺陷两侧界面的最大开裂量为0.991 mm，为缺陷初始厚度的49.5%。

3 结论

（1）随着间隙放电功率的增加，气隙温度迅速升高，相同放电功率下，温度随气隙厚度的减小而呈上升趋势，且放电功率越大，厚度的影响作用越明显。

（2）随放电功率增大，气隙面应力值呈单调上升趋势，其增幅大小与其所处位置的材料相关，硅橡胶-主绝缘气隙的应力变化较小，而半导电带-连接管气隙处的应力会迅速增大。随气隙压强增大，气隙面应力呈先下降后上升的趋势，气隙负压有增大局部应力效果，而气隙正压在一定区间内有减小局部应力的作用。

（3）间隙放电导致界面气隙呈收缩趋势，并在原气隙附近出现界面开裂现象，从而产生新气隙，且放电能量越高，新气隙的厚度越大。

（4）气隙负压对气隙和界面的作用效果与间隙放电时相似。而气隙正压导致原有气隙两侧界面出现开裂现象，气隙压强越高，气隙在厚度与面积上的扩张程度越大。

综合各项仿真结果，本文认为界面气隙缺陷会引起局部温度与应力分布的改变，并导致接头复合界面出现二次开裂现象，且随放电过程的积累而逐渐恶化，对绝缘材料造成危害。因此在电缆接头制作过程中应确保电缆本体与应力锥相接触的外半导电带端口切割平整，在复合界面处均匀涂抹硅脂，保证电缆在运行中各状态的对称性，避免因不均匀受力和受热而产生气隙。