盾构参数对复合地层损失率和地表沉降的影响
2022-04-25李宇健黄戡孙逸玮
李宇健,黄戡,孙逸玮
(长沙理工大学 土木工程学院,湖南 长沙410114)
在城市中进行地下空间的开发和施工时,需要着重考虑对地面沉降的控制。盾构法以开挖速度快、施工流程管理高效、地层适应性高等特点,在城市地铁建设中被广泛应用。盾构掘进过程中,由于地层参数条件在空间上的变化、地层变形与时间的相关性、施工参数的调整等因素,难以做到对沉降的精确预测。目前的研究方法主要有:经验公式法[1]、理论解析法[2-3]、修正经验公式法[4-5]、数值模拟法[6-7]、模型试验法[8-9]和人工智能神经网络法[10-11]。其中,经验公式法以Peck[1]公式为代表,Peck 于1969 年系统地提出地层损失的概念,认为开挖过程中产生的地表沉降是在不排水条件下产生的,是引起地层变形的首要原因。Peck 假定地表沉降槽的体积与地层损失相等,并给出公式计算地表沉降和地层损失率。数值模拟法在模型贴合实际条件的情况下能够反映土层性质,模拟施工过程,给出了土层深部的位移结果。郑刚等人[12]利用数值模拟软件,对隧道施工过程进行分析,通过分析实际地面沉降和盾构参数,模拟地面沉降和盾构参数的关系,推导出盾构参数相互之间的配合关系,以及各盾构参数对地表沉降的影响程度,但并未进一步研究盾构参数的变化对地层损失和地表沉降槽的影响。与此同时,关于在复合地层条件下盾构参数敏感度研究较少,而在复合地层条件下盾构掘进参数又非常多变。因此,本研究拟通过已有的施工沉降监测,利用Peck 公式反推盾构施工在该类地层条件下的地层损失率,模拟在复合地层条件下通过改变主要盾构参数,推断出盾构掘进各主要参数对地表沉降、地表沉降槽宽度和地层损失率的影响程度,并分析盾构穿越复合地层条件下地层变化对盾构参数的影响。
1 隧道引起的地层损失率
Peck 提出不排水条件下横向地面沉降估算公式为:


式中:S(x)为计算x点的地面竖向沉降;x为计算点到隧道中心的水平距离;Smax为隧道中心点上方最大地面竖向沉降;Vloss为隧道施工引起的单位长地层损失;i为地面沉降槽宽度,i=hk[13],k为地面沉降槽宽度系数,其主要由土性决定,h为隧道轴线埋深;η为地层损失率;R为隧道开挖半径。
联立式(2)~(3):

Peck公式的验证由式(1)得:

参考Burland[14]两边同时取对数:

如果实测数据符合Peck 公式,则式(6)为x2的线性方程,斜率为m= -1/( )2i2,此时对应的地面沉降槽宽度i为:

2 数值模拟
2.1 工程概况
长沙地铁6号线湖南商学院站至白鸽咀站区间的右线工程。该区间位于桐梓坡路下,沿道路敷设,道路宽度为46 m,双向6车道,现状地面高程起伏较大。该区间下穿桐梓坡西路,建筑物距离该区间净距均在20 m 以上,区间隧道对建筑物影响小。该区间左、右线为分修的2条单线隧道。区间左、右线隧道平面曲线最小半径为450 m,最大半径为600 m。隧道纵断面均为单坡,其中,坡度为25.5‰,竖曲线半径为3 000、5 000 m。线路轨面埋深16.8~21.2 m,轨面设计标高为39.234~19.593 m,隧道覆土11.8~16.2 m,隧道外径为6 200 mm,内径为5 500 mm。
2.2 建立数值模拟几何模型
有限元模型采用Midas gts nx软件建模,如图1所示。模型尺寸长50 m×宽50 m×深50 m。模型四周和底面边界x轴、y轴方向均无法位移,隧道主要穿越强风化板岩与中风化板岩,如图2所示。主要研究的部分为隧道穿越中风化板岩阶段,同时,弱化了边界效应对计算的影响。土体本构模型采用修正摩尔库伦本构模型,各地层参数设置见表1~2。采用Peck 公式反算法计算地层损失率,假定不排水,只考虑盾构开挖对土体造成的短期影响,不考虑盾构停机时间问题和长期固结。隧道管片部分采用板单元弹性本构模型,计算宽度1.5 m,厚度0.35 m,材料为强度等级C50混凝土,其弹性模量3.450×107kPa。由于盾构隧道管片通常采用错缝拼装的方式来提高管片的整体刚度,导致各拼接断面螺栓位置不同,故按照修正惯用法简化计算(管片接头处弯曲刚度的降低等效为等刚度均质管片环整体弯曲刚度的降低,并引入管片刚度有效率,再根据管片类型、接头类型和拼装方式等确定),针对本工程模拟计算采用的刚度有效率为0.7[15],管片材料弹性模量为2.415×107kPa,容重取25 kN/m3。布置横截面为D491 监测面,其位置在x轴正向第7排节点处。

图1 数值模型网格Fig.1 Grid of the numerical model

表1 各主要土层的物理力学指标Table 1 Physical and mechanical indexes of main soil strata

表2 各主要岩层的物理力学指标Table 2 Physical and mechanical indexes of main rock strata

图2 数值模拟监测面地质剖面(单位:mm)Fig.2 Geological profile of simulation monitoring surface(unit:mm)
2.3 开挖模拟
采用开挖模拟盾构掘进方式是以一环管片完整施工为一个阶段,然后一个阶段接一个阶段的完成向前掘进。掘进时,土舱压力F1通过均布压力的形式施加在前方掌子面上,掘进推力F2与土舱压力F1的差值作为盾构机壳体与周围土体之间的摩擦力F3,同步注浆(同步注浆压力F4)与管片的施工同时进行。
数值模拟设置不同的工况条件见表3,各盾构参数取值均符合设计范围值,以研究不同掘进参数对盾构隧道地表沉降与地层损失率的影响。

表3 数值模拟工况设置Table 3 Numerical simulation condition settings
3 数据的处理与分析
3.1 实际数据与模拟数据的处理与对比分析
有学者研究认为,土体开始固结的时间大约为盾尾通过后2 d,即取盾尾通过后第2 天测量的地面沉降量作为施工阶段不固结沉降量[4],监测值如图3 所示。从图3 中可以看出,盾尾通过D491监测面的3 d 前,地表轻微隆起,而在盾尾通过监测面的第2天出现增长速率较快地沉降,之后沉降增长速率减缓。速率较快的0~2 d造成地层损失的土体不固结沉降,之后缓慢沉降为土的固结沉降。故采用盾尾通过监测面后第2天的沉降量作为施工阶段沉降量,如图4所示。提取盾尾通过监测面的第2 天数据与Peck 公式进行拟合,如图5 所示,Peck 公式拟合结果表明:本次拟合的确定系数R²=0.827,可以判断实际检测数据的曲线图符合Peck曲线变化规律。

图3 盾尾通过D491监测面后的地面沉降与时间关系曲线Fig.3 Surface subsidence-time curve after the shield tail passes through D491 monitoring face

图4 盾尾通过D491监测面后的横向地面沉降曲线Fig.4 Transverse surface subsidence curves after the shield tail passes through D491 monitoring face.

图5 D491监测面2 d后的横向地面沉降曲线与Peck曲线拟合Fig.5 Transverse surface subsidence curve and Peck fitting curve in two days after the shield tail passes through D491monitoring face
通过整理监测面第2 天的地面沉降监测数据,利用Peck公式反推算法,绘制得到ln(S(x)/Smax)与x2的函数关系图,并做线性拟合,如图6 所示。其中,x为隧道中轴线的距离。线性拟合结果为曲线斜率m=-0.005 15,拟合确定系数R²=0.993。表明:该工程实测数据符合Peck 公式反推算法的适用条件,可以进行地层损失率的计算。根据式(7)代入m的值,得到i=9.853 m,再将i值代入式(4),得到η=1.22%;H/D=2.42;沉降槽宽度系数k=0.656 9,得到的k值相较于Peck[1]提出的k=0.5(H/D)1-n(n=0.8~1)计算出的k值(0.500 0~0.596 7)大。韩煊等人[16-18]提出的k=1-0.02φ,φ为土体的内摩擦角,(°)。计算得到开挖面上方土体内摩擦角平均值φ=17.085,从而得到k=0.658 3,更加适用于本工程工况k值的预估计算。

图6 实测数据Peck公式反算法回归分析Fig.6 The measured data of Peck formula method regression analysis
由于地表沉降槽的取值宽度为5i[19],数值模拟结果数据的提取节点数固定,导致地表沉降槽宽度取值与5i不匹配,故采用Peck 公式拟合处理方式来处理地表沉降值的结果。为了对应盾尾通过监测面2 d 且沉降增加幅度减小,取开挖面距离监测面8 环后的地面沉降值如图7 所示,进行地层损失率的计算,计算结果如图8所示。Peck公式拟合曲线地表沉降槽宽度为i=8.249 m,拟合确定系数R²=0.997,将i代入式(7)得η=0.857%。从图8中可以看出,工况一数值模拟虽然在沉降值的数值大小上与实际监测有差别,但沉降槽宽度的计算结果相近,考虑到实际施工过程的复杂性与地层条件的多样性,数值模拟可以在一定程度上反映沉降与地层损失率二者的变化规律。

图7 工况一开挖通过D491监测面后的横向地面沉降曲线Fig.7 TTransverse surface subsidence curves after the shield tail passes through D491 monitoring face under Case 1

图8 工况一开挖通过D491监测面8环后的横向地面沉降值与Peck曲线拟合Fig.8 Transverse surface subsidence values and Peck fitting curve in 8 rings later the shield tail passes through D491 moni toring face under Case 1
3.2 各工况模拟数据的处理与分析
用与工况一相同的方法,处理其他工况的数据,得到沉降槽宽度与地层损失率见表4。由表4可知,对比工况一、工况二、工况三,可得:在其他参数相同条件下,掘进推力增大时,沉降槽宽度减小,沉降值增大,地层损失率增大。这些变化符合高斯沉降曲线在覆跨比H/D与工程地质条件不变(即地面沉降槽宽度系数k不变)的情况下,沉降槽宽度随沉降值的增大而减小。对比工况一、工况六、工况七,在其他参数相同条件下,土舱压力增大时,沉降槽宽度减小和沉降值增大,虽不明显,但仍然符合工况一、工况二、工况三的变化规律。对比工况一、工况四、工况五,其他参数保持不变,在注浆压力增大时,沉降槽宽度减小,沉降值减小,地层损失率也减小。表明:注浆压力的增大,浆液可快速填补盾尾间隙,向周围土体施加法线外方向的力,并使管片发挥支护效果具有积极作用。

表4 各模拟工况D491监测面地面沉降参数Table 4 D491 monitoring surface subsidence parameters under each simulated condition
对比掘进推力对地表隧道中轴点的沉降影响,如图9(a)所示,掘进推力在300~600 kPa 过程中,沉降值S随着盾构掘进推力F2的增大,即摩擦力F3的增大而增大,并且通过对比300~455 kPa 与455~600 kPa 发现,沉降变化速率ΔS也随着掘进推力F2的增大而增大。其主要原因是:①摩擦力的增大导致对周围土体的扰动变大。②对比刀盘驶入、盾尾脱出、盾尾脱出4 环后和盾尾脱出8 环后,发现盾尾脱出后同步注浆与管片无法提供盾构机壳体施加给周围土体一样的作用力,土体出现的瞬时沉降更明显。表明:在盾构机穿越较硬地层后,到达较软地层时,需要严格控制掘进推力。
盾尾同步注浆压力增大,地表沉降值S减小,但注浆压力的影响程度不大,沉降值的变化在盾构掘进阶段之间的差别如图9(b)所示,主要起到快速填充盾尾处管片与土体之间空隙的作用。
盾构土舱压力F1增大,地表沉降值S增大,增幅不明显,如图9(c)所示。分析产生差异的主要原因有:①本工程设计的盾构掘进参数中,土舱压力的范围值贴合该工程的地质条件,使得土舱压力始终在较为合理的范围内波动,不会对前方土体造成过大的扰动。②本工程使用的盾构机在计算机控制器的基础上,建立了土舱内土渣保压、膨润土保压和结合地层气密性气压保压的联合保压系统。通过计算机精确控制,及时调整土舱内的压力,保障开挖面的支撑稳定,使土舱压力偏差值小。③本研究主要针对盾尾脱出后土体不排水沉降,土舱压力主要影响开挖面稳定,因而不是主要影响因素。
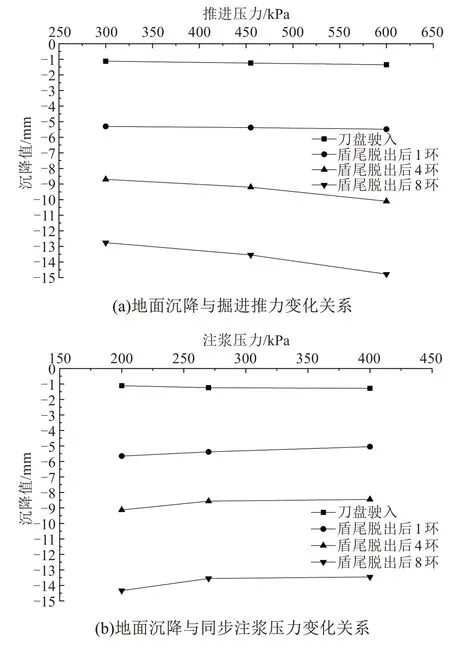

图9 各阶段地面沉降随盾构参数变化Fig.9 Variation of surface subsidence with shield tunneling parameters in each stage
3.3 盾构机穿越上软下硬地层时盾构参数分析
隧道的地质情况如图10 所示。从图10 可以看出,盾构机在85 环至105 环开挖部分中风化板岩占比较大。随着盾构地掘进,盾构参数的变化如图11 所示,其中,87~100 环掘进时间见表5。从图11(a)和表5 可以看出,掘进压力减小幅度约为80 kPa,主要是由于前方的土体强度较高,千斤顶需要配合刀盘转动,降低掘进速度,完成对较高强度土体的切削。从图11(b)和表5 可以看出,同步注浆压力在开挖至87 环后增幅约为100 kPa,并且在开挖至100环之前都维持了较高的平均值,是因为掘进速度变慢而导致注浆压力变大。从图11(c)中可以看出,盾构开挖至87 环后土舱压力出现了增长,由160 kPa增长至180 kPa,这是由于前方开挖面的土体密度增大,而土舱压力为平衡前方水土压力进行了一定调整,随后开挖面后方的土体逐渐变为强风化板岩,土舱压力也就下降。

图10 盾构隧道与地层位置关系Fig.10 Relationship between shield tunnel and stratum position

图11 盾构参数随盾构掘进变化Fig.11 Changes of shield parameters with shield tunneling

表5 87~100环掘进时间Table 5 Driving time of rings 87~100
由表4还可知,与工况一实际参数设置相差越大的工况,其模拟结果沉降值也相差越大。例如:在90~100 环中,工况四设置的同步注浆压力为400 kPa,比工况五设置的同步注浆压力值200 kPa更接近工况一设置的平均值360 kPa,沉降值相差也更小。掘进推力对地表沉降影响更大,在85~100 环的开挖部分如果不能及时调整掘进推力,将造成更严重的沉降影响。
4 结论
以长沙地铁6号线湖南商学院站至白鸽咀站盾构区间,穿越上软下硬地层时,盾构机的施工参数和监测横断面的实测数据为依据。针对盾构机在正常掘进过程中掘进推力、同步注浆压力和土舱压力3个参数对周围土体的地层损失率和地表沉降的影响进行分析,得出以下结论为:
1)长沙地铁6 号线湖南商学院站至白鸽咀站盾构区间的覆跨比H/D为2.42,沉降槽宽度系数k=0.656 9,地层损失率约为1.22%。
2)根据该工程土压平衡式盾构机掘进参数,以控制地层损失率和地表沉降值作为分析目标,分析3个主要的盾构参数,得出对地层损失率和地表沉降值的影响程度,从大到小的顺序依次是:掘进推力、同步注浆压力、土舱压力。其中,同步注浆压力的大小变化与地层损失率、地表沉降值的大小变化成反比。
3)根据该工程施工台账记录的盾构掘进参数进行分析,当盾构穿越上软下硬地层时,盾构机掘进速度的变化是影响盾构参数变化的直接原因。当开挖面后方土体强度、密度增大时,土舱压力也会增大,掘进速度减慢,掘进推力减小,同步注浆压力增大。当开挖面后方土体强度、密度减小时,土舱压力减小,掘进速度加快,掘进推力增大,同步注浆压力减小。故在盾构穿越复合地层的过程中需要时刻注意地层变化,及时调整盾构掘进参数,将沉降量与地层损失率控制在设计范围内。
