基于CFD 气囊—导管架系统拖航水阻力分析

王佐强，章仲怡，景雪娇，唐友刚*

（1.中海油能源发展股份有限公司清洁能源安装分公司，天津 300452；2.天津大学建筑工程学院，天津 300350）

气囊助浮拆除导管架后，气囊—导管架系统需湿拖到码头，拖航阻力的计算对于确保气囊—导管架系统的拖航安全十分重要。目前，国内针对船舶及海洋结构物海上拖航阻力计算已经开展了较多研究工作。杨西阳[1]分析了拖航过程不同阻力的成因，但是其分析主要适用于船型结构。中国船级社天津分社研究了钻井平台的拖航阻力，总结出了海上钻井平台的拖航阻力计算公式[2-3]，船级社颁布的拖航阻力计算方法和钻井平台拖航阻力计算方法，主要适应于船型结构拖航。上海打捞局沈浦根[4-5]在其多年实践经验的基础上，参考国内外文献及船级社规范，总结出了拖航阻力估算公式，该计算方法考虑了结构迎水面的形状、附着物等对于阻力的影响，但是该阻力估算方法研究的基础还是海上船型结构的拖航阻力。 基于CFD（Computational Fluid Dynamics）计算大型海洋结构拖航阻力，是近几年发展的新方法，曾祥堃等[6]基于CFD 方法，计算大型沉井结构，刘为民等[7]计算半潜式钻井船拖航阻力，但是其结构特点仍然是以摩擦阻力为主。船型结构的拖航阻力方法已基本成熟，于常宝等[8]分析了FPSO（Floating Production Storage and Offloading）的拖航阻力。李伟峰等[9]基于港口规范计算波浪载荷，计算钻井平台拖航过程波流及风引起的拖航阻力，该结构拖航水阻力主要是船型结构的阻力。张立等[10]通过试验研究，分析拖航过程工程船舶不同阻力的成因，分析了波浪、风、海流阻力的比重。目前的研究现状表明，钻井装置及FPSO 拖航过程中的阻力主要成因是船型结构与海水的摩擦，目前对于导管架一类杆状结构的拖航阻力计算方法研究较少。

本文提出的采用气囊助浮拆除导管架是一种创新技术，国内外尚无先例，针对该系统拖航阻力的计算也未见报道。本文针对绑扎气囊的导管架系统，采用CFD 方法和船级社颁布的钻井装置拖航阻力计算公式，分别计算得到气囊—导管架系统的拖航阻力。比较两种方法的计算结果，可以看出基于CFD 方法计算复杂形状结构拖航阻力的可行性，该计算方法对于气囊助浮拆除导管架，起到了技术支撑作用，对于此类结构的拖航阻力计算，也是一种新的探索和尝试。

1 CFD 计算导管架系统阻力的基本理论

1.1 理论方程

CFD 方法是在满足能量守恒、质量守恒、动量守恒方程的前提下，对流体流动进行的数值模拟方法。基于该模拟方法，可以得到流场内不同位置的压力、速度等物理量随时间和空间的分布规律。CFD 方法的基本理论由如下方程构成。

流场内流体运动满足流体质量守恒方程如下。

式中，ρ 为流体密度；t 为时间；vx、vy及vz分别为X、Y、Z 方向流体速度。此外，求解过程还需要满足动量守恒的条件，流场内水质点X、Y、Z方向的动量方程如下。

式中，u 为速度分量，ux、uy及uz分别为X、Y、Z 方向的速度；τ 为剪切力；fx、fy及fz分别为X、Y、Z 方向的力。CFD 方法通过特定的算法建立起流场内不同点上物理量之间的代数方程组，求解方程组得到流场内不同流体质点的速度和压力数值解。

1.2 离散方法

在进行CFD 方法模拟计算之前，需要对计算的流体域进行离散化处理。离散化是指将流域中的连续流体划分为若干子区域（称为流体单元），确定每个单元的中心后生成计算网格。

本文对N-S 方程及VOF 输运方程均使用有限体积法（Finite Volume Method，FVM） 进行离散。有限体积法将计算域离散为一系列的小单元，从而将计算出的流场信息存储在网格单元的中心，再根据单元中心数据进行插值，就可以得到单元面上的值。根据高斯理论，将单元表面的值相加即可得到单元体的体积积分。有限体积法导出的离散方程可以保证具有守恒特性，而且离散方程系数的物理意义明确，是目前流体流动问题数值计算中应用最广泛的一种方法。

上述有限体积法将N-S 控制方程转化为了代数方程组，但是求解时还需要选择不同的求解方式。本文选用FLUENT 求解器，应用CFD 的传统离散算法PISO（Pressure Implicit Split Operator）。PISO算法通常用于瞬态计算，计算时，为了计算结果的稳定，通常规定其库朗数不可大于1。PISO 算法的优势是允许使用较大的时间步长进行计算，因而在允许使用大时间步长的计算中可以缩短计算时间，且可以处理网格畸变较大的问题。

2 CFD 计算拖航阻力

2.1 气囊—导管架系统参数

本文海上拖航的目标结构物是渤海湾废弃的海洋导管架结构，气囊绑扎在导管架上，帮助导管架漂浮在海面上实施拖航。导管架结构的主要参数见表1。

表1 目标导管架的主要结构参数

导管架自身的重量为782.8 t，高度为19.6 m，海域水深为7.8 m，导管架漂浮状态吃水为5.5 m，结构浮心坐标为（0.24，0，-1.45）。绑扎气囊提供助浮力，气囊直径为2.0 m，长度为14.8 m，共24个气囊，气囊的主要参数见表2。

表2 气囊的主要参数

导管架浮起前，气囊助浮单元与导管架左右两侧绑扎位置为高程范围-9.1～5.1 m，前后两侧绑扎位置为高程范围-8.9～4.9 m，气囊分为6 组与导管架相连，连接位置如图1 和图2 所示。

图1 气囊配置示意图

图2 连接气囊的导管架结构示意图

2.2 CFD 建模

采用CFD 软件，基于三维湍流模型进行拖航阻力数值模拟。本文模拟导管架拖航阻力时，结构处于气—液两相的环境中，因此选用气—液两相流体的模型。对自由液面的模拟和跟踪采用VOF（Volume of Fluid）方法，引入体积分数，通过计算每个网格单元的流体体积分数构造运动界面，进而确定水表面位置。为了更好地模拟流场中层流的状态，在导管架周围添加边界层网格。为了模拟气囊—导管架系统在波浪中的拖航状态，采用软件中的明渠流进行数值造波，构造波浪数字水池。为了完成对N-S 方程的有效求解，需要引入湍流模型。本文主要采用海洋工程领域CFD 应用最为广泛的剪切应力传输（Shear Stress Transfer，SST） k-ω 湍流模型进行求解。该模型计算效率高，准确度好，结合了标准k-ω 和k-ε 模型的优点。为了保证CFD计算结果的准确性，计算时需要考虑收敛条件判断数（Courant Friedrichs Lewy，CFL），保证CFL ＜1。采用压力隐式分裂算子（Pressure-Implicit with Splitting of Operators，PISO）格式建立了离散方程，进行非稳态模拟。计算选取的时间步长与非定常模拟有关，时间步长值中的错误可能会使输出模拟状态不佳。在该仿真中，时间步长为0.01 s，符合国际拖曳水池会议（International Towing Tank Conference，ITTC）准则。计算总时间取为30 s。

建立气囊—导管架系统CFD 模型如图3 所示。导管架平台模型分为3 层，气囊位于最下面一层，共绑扎有气囊24 个。

图3 气囊—导管架平台模型示意图

建立流域模型如图4 所示。流域长450 m，宽200 m，深20 m。模拟拖航时的状态，气囊—导管架吃水为5.5 m，流域流速为0.6 m/s，拖航方向为迎流向。

图4 计算流域与边界条件示意图

对长方体计算流域的6 个面进行边界条件定义：（1）右边界面：速度入口边界条件，流体从此边界均匀流入；（2）左边界面：自由出流边界条件，流体从此边界自由流出；（3）上边界面：对称边界条件，此边界上垂直方向分量为0；（4）下边界面：壁面边界条件，流体从壁面无滑移流过；（5）前、后边界面：对称边界条件，此边界上垂直流向分量为0；（6）导管架表面：壁面边界条件，流体从壁面无滑移绕过。

计算采用Fluent 软件VOF 模型的Open Channel Flow 选项，设定相数为2，使用Open Channel Wave BC 造波，构造随机波浪采用JONSWAP 波浪谱，波高为1.0 m，波浪平均周期为4 s。

模型采用非结构化网格。为了更好地模拟自由液面和波浪，更好地模拟导管架拖航运动过程中产生的流体漩涡，提高模拟的精度，对靠近导管架、自由液面和水体区域的网格进行加密处理。模型最终网格单元数为8 695 632，节点数为1 478 078。

2.3 网格无关性验证

为了对拖航速度为2.06 m/s（4 kn）的工况进行网格无关性验证，本文将模型做不同精细程度的网格划分，3 个不同精细程度的模型网格数量分别为6.64×106、8.69×106和9.62× 106。海水阻力的时间历程曲线如图5 所示。模拟都是在相同的硬件环境中进行的，并考虑了30 s 的运动总时间成本。

图5 不同网格数量下的模拟结果对比

选取受阻力波动较为稳定的时间段10～20 s 为稳定段，计算其平均拖航阻力作为拖航阻力的模拟结果。3 个不同数量网格模型的拖航阻力结果如表3 所示。

表3 3 个不同数量网格模型的拖航阻力结果

由图5 及表3 可以看出，3 种网格模型的计算结果具有很好的一致性，计算结果差异小于0.1%，说明计算对于网格密度变化的敏感性很小，验证了计算结果的网格无关性。由于精细模型的网格数量过大，过于消耗计算资源，考虑到计算时间成本问题，本文之后的计算均采用6.64×106网格数的网格模型，既保证了计算结果的准确性，又节约了计算资源。

2.4 拖航阻力计算结果

针对拖航速度分别为2.06 m/s、2.57 m/s、3.09 m/s（4 kn、5 kn、6 kn）的各工况计算拖航阻力。由于非线性的影响，CFD 方法计算模拟过程是非稳态的，气囊—导管架所受拖航阻力大小随时间发生变化，在计算过程中观察阻力的计算结果，直到阻力的大小保持基本稳定后停止计算，模拟得到如图6中不同拖航速度下结构物所受海水阻力的时间历程曲线。

图6 气囊—导管架系统拖航水阻力

从水阻力的时间历程曲线可以看出，在模拟时间10～20 s 内，导管架所受海水阻力波动较为稳定，因此取模拟时间10～20 s 为稳定段。取稳定段的平均阻力大小作为拖航过程中的海水阻力结果，得到表4 中CFD 方法拖航水阻力计算结果。

表4 CFD 方法计算结果

由表4 可知，拖航水阻力组成项中，海水阻力为拖航阻力的控制因素，该阻力由平台拖航时水线以下结构物的构型和拖航速度共同决定。气囊—导管架系统的涡量图如图7 和图8 所示。

图7 气囊附近涡量图

图8 导管架桩腿涡量图

可以看出，在拖航过程中，气囊周围和导管架桩腿附近产生了大量漩涡，尤其在气囊周围的流体中，由于气囊的扰动和流体的黏性，产生的漩涡更多，这些涡量的产生，是引起拖航水阻力的重要原因，这些涡量随拖航速度的增加而大幅增加，CFD方法可以很好地模拟这些涡量的产生，从而可以得到合理的拖航阻力计算结果。

3 海上钻井装置的拖航阻力估算方法

计算气囊—导管架系统的拖航阻力的公式如下。

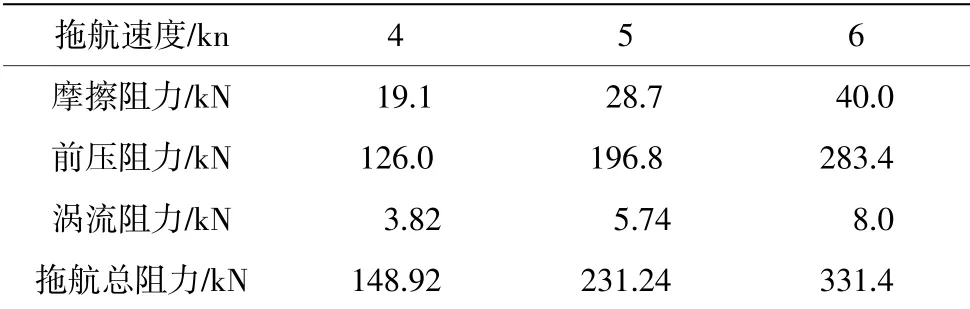
表5 钻井装置水中阻力估算方法计算结果

4 计算结果对比分析

采用船级社颁布的钻井装置拖航阻力方法、海上拖航指南和CFD 方法计算拖航阻力结果总结见表6。

由表6 可知，CFD 方法得到各个航速下的拖航阻力，均大于海上钻井装置拖航阻力估算方法及海上拖航指南计算得到的拖航阻力。对于本次气囊—导管架系统拖航，气囊部分浸没水中深度为3 m，吃水为5.5 m，导管架6 个桩腿外伸出气囊以下2.5 m，外伸6 个桩腿的拖航阻力在公式中没有考虑；此外，按照钻井装置拖航水阻力公式和海上拖航指南计算结果，摩擦阻力所占比重很大，而非线性漩涡阻力仅为摩擦阻力的20%，这在船型结构拖航阻力中是合理的，而对于本文的气囊—导管架系统水阻力计算则不合理，从图7 和图8 可以看出，漩涡引起的阻力比例大于20%，这是钻井装置拖航阻力公式和海上拖航指南计算水阻力偏小的重要原因。

表6 3 种方法计算结果对比

5 结 论

本文针对气囊—导管架系统拖航，创新提出了CFD 方法计算拖航阻力，建立气囊—导管架系统的CFD 模型，考虑波浪和流共同作用计算拖航阻力，并且与通用钻井装置拖航阻力公式计算结果进行比较，得出主要研究结论如下。

（1）钻井装置拖航阻力计算公式，更适合于船型一类结构物的拖航阻力计算，对于气囊—导管架系统的拖航阻力计算结果不合理。

（2）气囊—导管架一类杆状结构的组合体与船型结构的阻力区别在于，船型结构阻力主要是摩擦力，而气囊—导管架一类结构拖航阻力主要由非线性拖曳力和漩涡引起，尤其气囊周围的漩涡阻力，是引起拖航阻力的重要原因。采用CFD 方法对拖航过程进行模拟，能很好地模拟出流体的漩涡阻力，因此，本文提出的CFD 计算方法是一种较为准确的仿真方法。

（3）CFD 方法计算导管架结构的拖航阻力是一种可行的方法，可以较为全面地考虑杆状结构的拖航阻力因素，包括拖曳阻力和漩涡阻力，该方法是一种计算杆状组合结构拖航阻力的有效方法。本文研究结果表明，基于CFD 方法计算气囊—导管架系统的拖航阻力是一种有效方法，建立的分析模型可以很好地模拟气囊—导管架系统的水阻力特性。