GNSS 测量法在长距离跨海高程传递中的应用
2022-04-25董斌斌刘远海周建营陈国恒
董斌斌,刘远海,周建营,陈国恒
(广东省国土资源测绘院,广东 广州 510500)
内陆跨河水准测量中的全球导航卫星系统(Global Navigation Satellite System,GNSS) 测量法主要是基于高程异常的变化率进行高程传递,基本方法是使用GNSS 接收机和水准仪分别测定两岸点位的大地高差和对应点位的水准高差,然后求出两岸的高程异常和两岸高差[1]。相对而言,该方法实施方便,且受外业观测条件影响相对较小,可延伸用于长距离的跨海高程传递。我国早在20 世纪90年代就有专家提出了利用全球定位系统(Global Positioning System,GPS)水准结合重力大地水准面进行长距离跨海高程传递测量的方法,将国家高程基准传递到距离陆地约30 km 的洋山岛上,传递后的两段高程差与三等水准测量结果相近[2],也有不同的学者基于GNSS 测量法,分别在跨海隧道、跨河/海大桥和岛礁测绘等工程中实现了跨海高程传递[3-6]。然而,如何在该方法中选择合适的布点方案及分析手段,更高效地建立陆岛或远岛礁间的高精度高程联系,却是目前广东省全面构建陆海一体现代基准体系亟须解决的问题。为此,本文结合广东省岛礁的地形地貌特点,利用GNSS 测量法分别在离大陆约8.2 km 和12.6 km 的岛礁上实现了高程基准传递,与原精密三角高程法比较,GNSS 测量法能达到规范规定的精度,为长距离的跨海高程传递提供了方法参考。
1 原理与方法
1.1 常规方法
《国家一、二等水准测量规范》[1]规定,GNSS 测量法采用GNSS 观测与水准测量,求取跨海两岸各点间的大地高差与正常高差。其中GNSS 观测等级根据跨海长度而定,水准测量则采用二等及以上水准测量。高差计算如图1 所示。
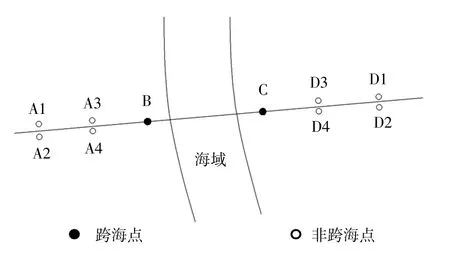
图1 高差计算示意图
A、B 两点间的高程异常变化率的计算公式如下。
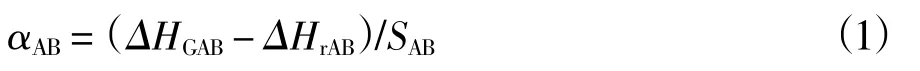
式中,αAB为AB 方向的高程异常变化率,单位:m/km;SAB为A、B 点间的平距,单位:km;ΔHGAB为A、B 点间的大地高差,单位:m;ΔHrAB为A、B点间的正常高差,单位:m。
根据公式(1)由每一个非跨海点与最近跨海点计算出一个α 值,最后将海域两岸得到的不同的αAB与αCD取平均值作为跨海段的高程异常变化率αBC。海域两岸得到的不同的α 值(αAB、αCD)较差应满足表1 的规定[1]。

表1 高程异常变化率规定表
高程异常差按式(2)计算。

式中,ΔξAB为A、B 点间的高程异常差,单位:m。
跨海线路BC 之间的跨海水准高差计算公式如下。

式中,各符号意义同A、B 之间。
1.2 高差拟合法
当跨海距离尚未达到省、市级别的地区范围时,局部区域高程异常具有相关性,可通过跨海两岸的GNSS 水准点间的高程异常变化,并采用简单模型对跨海区域进行高差拟合[7-8]。目前常用的拟合模型有直线、二次曲线、三次曲线、平面模型和曲面模型等[9-10]。当只考虑沿跨海方向高程异常的变化时,可采用直线或曲线拟合的方法。首先是建立跨海坐标系[11],如图2 所示,以非跨海点作为坐标原点o′,以跨海点连线的延长线方向作为x′,过原点o′且与x′轴垂直方向为y′。当跨海点与非跨海点沿x′轴分布时,则可忽略y′轴方向高程异常的变化。
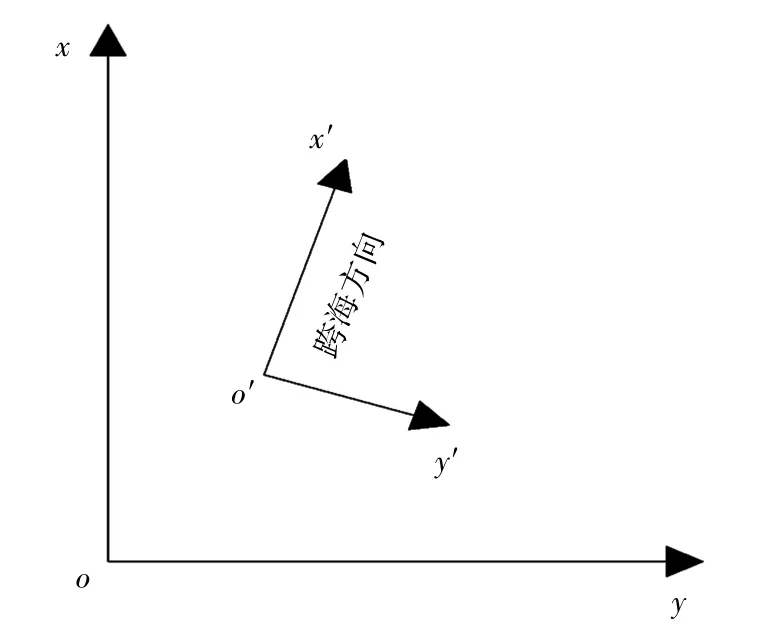
图2 跨海独立坐标系示意图
三次曲线GNSS 高程拟合的计算公式如下[12]。

式中,α0、α1、α2、α3为拟合系数。由于在GNSS跨海高程传递中,只能获得同岸点位的正常高差值,因此将式(4)改为高差拟合模型,根据图1 的点位分布,计算公式如下。

式中,若只考虑等式右侧第1 项,则计算退化为直线拟合模型,若只考虑前2 项,则退化为二次曲线拟合模型。α1、α2、α3计算公式如下。

式中,ΔξAB、ΔξBC、ΔξCD为A 和B、B 和C、C和D 各两点间的高程异常差,进行三次曲线拟合需要不少于3 段高差。
当跨海区域分布多个高差段时,也可采用平面模型和曲面模型进行高差拟合。平面拟合计算公式如下。

式中,αx、αy为x、y 两个方向的拟合系数,进行平面拟合需要不少于2 段高差。
截至2016底,黑龙江省已建成运行的秸秆直燃发电项目32个,总装机容量约为610MW,占全国总装机容量的11%左右。
曲面拟合计算公式如下。
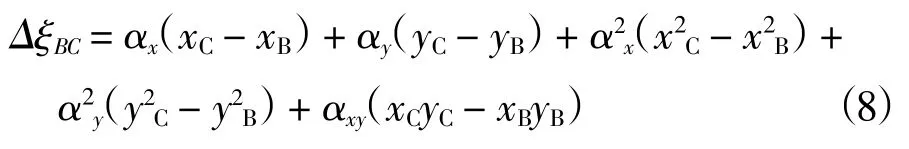
式中,αx、αy、α2x、α2y、αxy为x、y 两个方向的拟合系数,进行曲面拟合需要不少于5 段高差。
2 实例分析
2.1 试验场布设
本次试验区位于江门市台山川岛镇,点位布设示意见图3。

图3 试验场布设示意图
试验场有2 个跨海段,跨海段1(B013—B016)距离约8.2 km,按2 个方案进行非跨海点的选埋。方案1:在两跨海点B013 和B016 的延长线上选埋B009 和B010、B023 和B024 两组非跨海点,且每组点间距与跨海距离按规范要求保证大致对称和相等。方案2:在B013 和B016 延长线上选埋B011和B012、B021 和B022 两组非跨海点,每组点与跨海点的间距约为1/2 跨海距离。跨海段2(B014—B017)距离约12.6 km,同样按2 个方案进行非跨海点的选埋,B005 和B006、B007 和B008、B027 和B028 的布设方式同跨海段1 的模式,B025和B026 由于地形限制,点位与跨海点B017 的距离约为1/14 跨海距离。
2.2 常规方法分析
本次试验在跨海段1 和跨海段2 所在区域完成了GNSS 观测和二等水准测量。GNSS 数据采集使用12 台天宝R8S 接收机以网连式的形式分组观测共16 个点位,其中以B013、B014、B016、B017共4 个跨海点连续固定观测,每组观测时长96 h,接收GNSS 卫星信号,数据处理采用4 星系统分别解算与联合平差[13],解算各项指标均满足规范要求,并以4 个跨海点作起算基准进行平差计算,获得高精度的点位大地高,其点位精度均优于1.5 mm。各项高差段计算结果见表2 和表3。
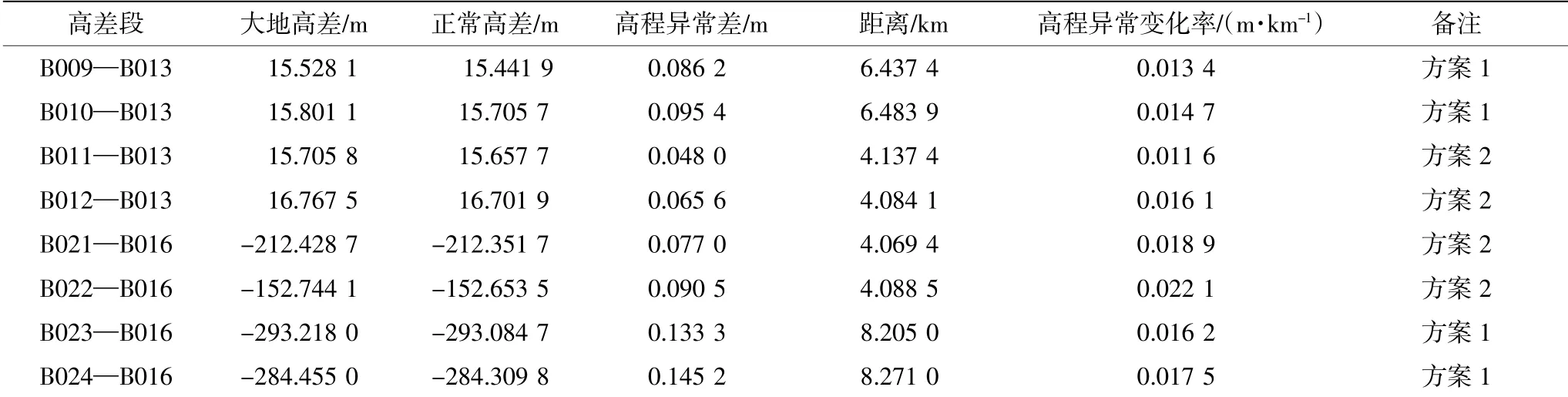
表2 跨海段1 高差计算结果统计表
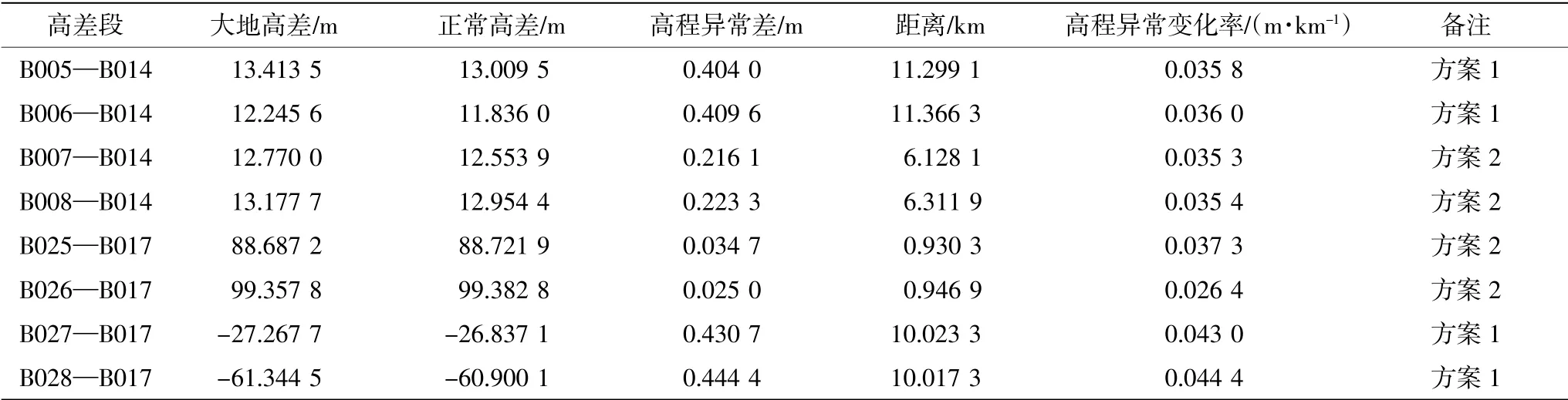
表3 跨海段2 高差计算结果统计表
由表2 可以计算得出,跨海段1(B013—B016)用方案1 测量的平均值为0.015 5,正常高差值为-7.657 3 m;用方案2 测量的平均值为0.017 2,正常高差值为-7.671 2 m。此外,还可以进一步计算得出,方案1 和方案2 在同岸或不同岸两种情况下,跨海段1 中的高程异常变化率较差值。计算结果以及对应的规定限差[1]见表4。
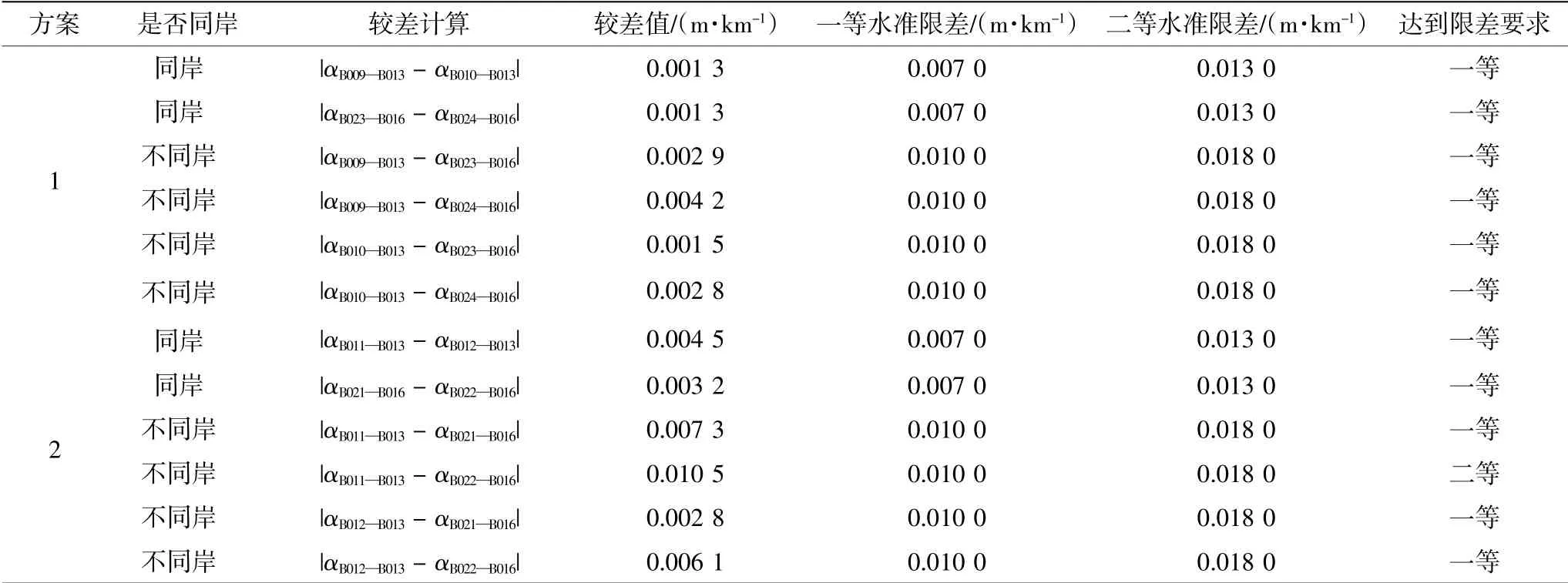
表4 跨海段1 高程异常变化率较差值
类似地,由表3 可以计算得出,跨海段2(B014—B017)用方案1 测量的平均值为0.039 8,正常高差值为168.410 7 m。方案2 中两岸的非跨海点距离不相等,导致了不同岸的值较差均大于二等水准限差(0.018 0)要求,取平均计算获得值为0.033 6,则跨海段2(B014—B017)的正常高差值为168.489 0 m。此外,还可以进一步计算得出,两种方案在同岸或不同岸两种情况下,跨海段2 中的高程异常变化率较差值。计算结果以及对应的规定限差[1]见表5。而各高差段与现有的精密三角高程测量成果[14-16]比较以及对应的规定限差[1,17]见表6。
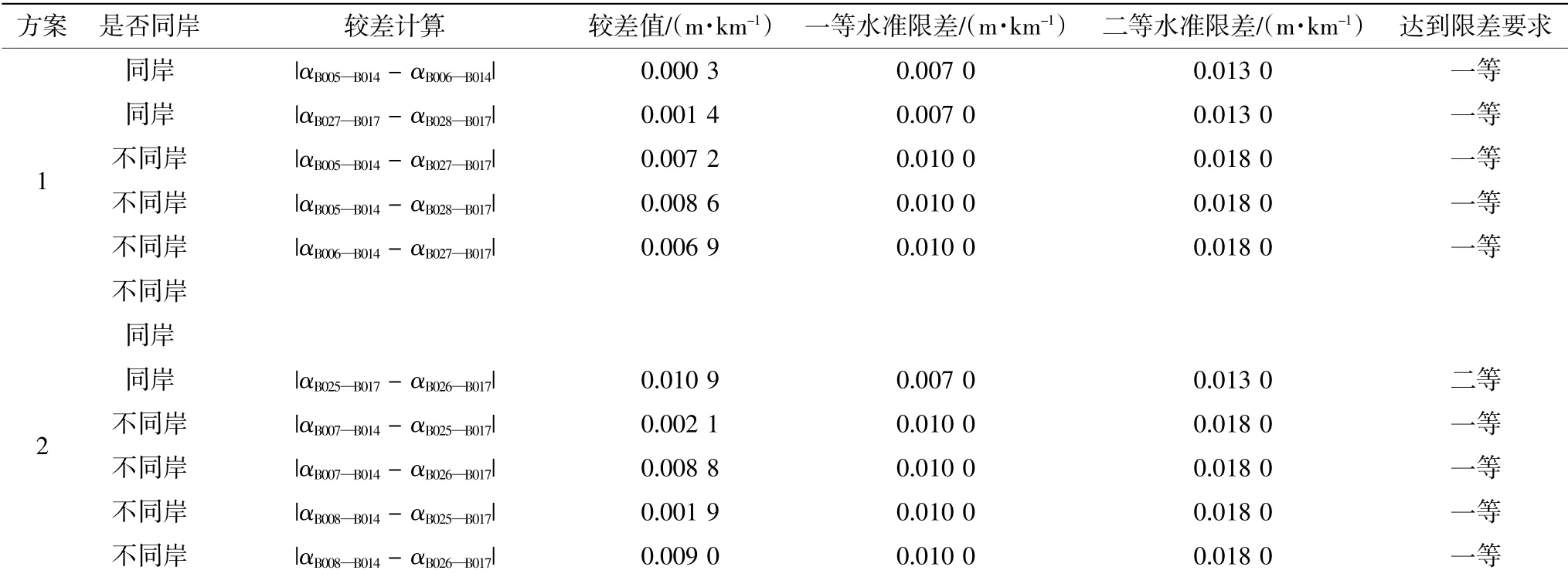
表5 跨海段2 高程异常变化率较差值

表6 高差对比表
由表6 可得,跨海段1 现有的精密三角高程法得到的高差值与方案1 的较差为13.7 mm,能满足二等水准检测限差(6,R 为检测测段长度,单位:km)的要求,与方案2 的较差仅为0.2 mm,能满足一等水准检测限差(3)的要求[1]。跨海段2 现有的精密三角高程法与方案1 的较差为32.3 mm,与方案2 的较差为46.0 mm,均不满足一等和二等水准检测限差要求,但满足三等(20)和四等(30)水准检测限差要求[14]。因此,对于规范中采用的基于高程异常的GNSS 测量法而言,在约8.2 km 的跨海段1 采用跨海点和非跨海点间距大致相等(方案1)或间距不相等但对称(方案2)的形式,计算得到的高程异常变化率较差值均可满足二等的要求,高差值与精密三角高程法相比能满足二等检测限差要求,该跨海段方案1 和方案2 的精度相当。在约12.6 km 的跨海段2 采用跨海点和非跨海点间距大致相等(方案1)或间距不相等且不对称(方案2)的形式,计算得到的高程异常变化率较差值虽可满足二等的要求,但高差值只能满足三等水准检测限差要求,该跨海段方案1的布点形式精度优于方案2。
2.3 高差拟合法分析
根据本次试验场的布点方式,采用直线或曲线拟合时,尽量选择沿x′轴线性分布的点位,以减少y′轴方向高程异常的变化影响。因此,跨海段1 选择B009、B011、B013、B016、B021、B023 共5 段高差,其中B013—B016 为待求高差,其余4 段为内符合段。跨海段2 选择B006、B008、B014、B017、B025、B027 共5 段高差,其中B014—B017为待求高差,其余4 段为内符合段。分别采取直线拟合、二次曲线拟合和三次曲线拟合进行计算。高差拟合和各已知测段的内符合精度统计,以及各测段的二等水准限差(即二等水准的测段高差不符值4,k 为测段距离,单位:km)、三等水准限差(即三等水准的测段高差不符值12)、四等水准限差(即四等水准的测段高差不符值20),如图4 和图5 所示。
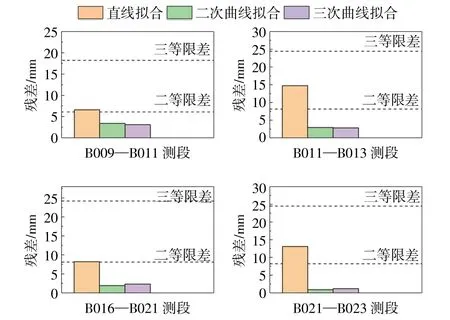
图4 跨海段1 直线和曲线拟合内符合精度统计图
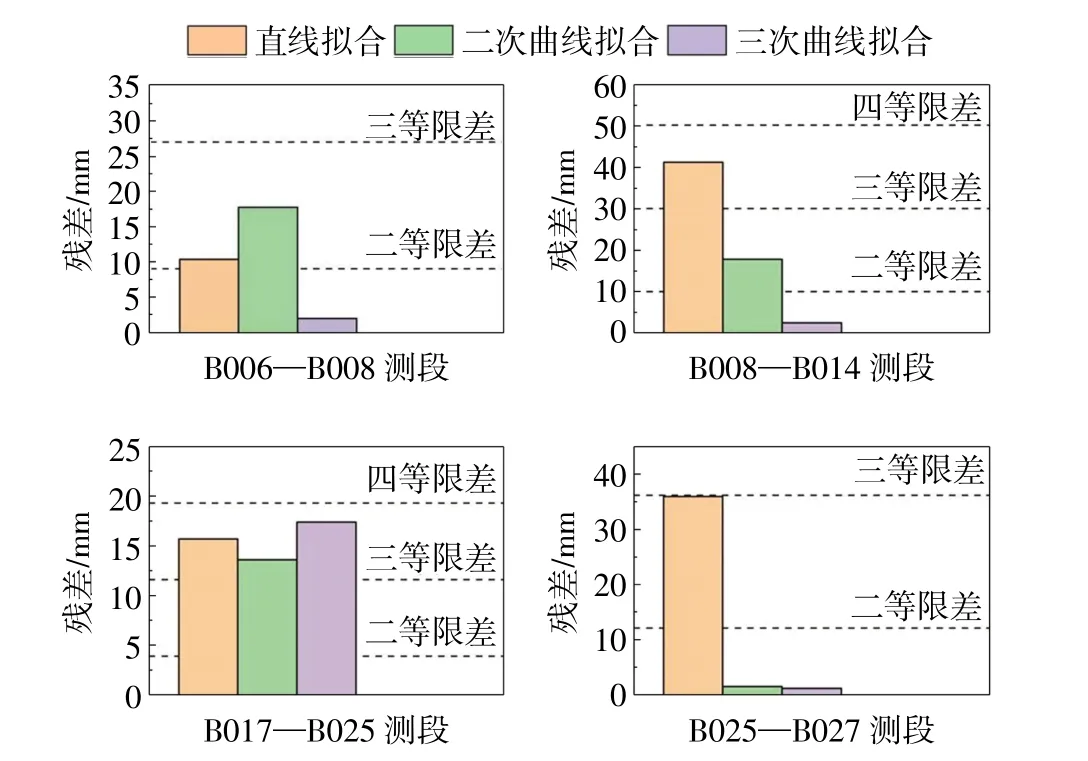
图5 跨海段2 直线和曲线拟合内符合精度统计图
由图4 可知,对于跨海段1,三次曲线拟合的内符合精度最优;由图5 可知,对于跨海段2,整体上三次曲线拟合内符合精度最优。
对于平面拟合和曲面拟合,可充分利用已有2个跨海段共18 段高差进行计算。高差拟合和各已知测段的内符合精度统计如图6 所示。
由图6 可知,整体上曲面拟合内符合精度略优于平面拟合。
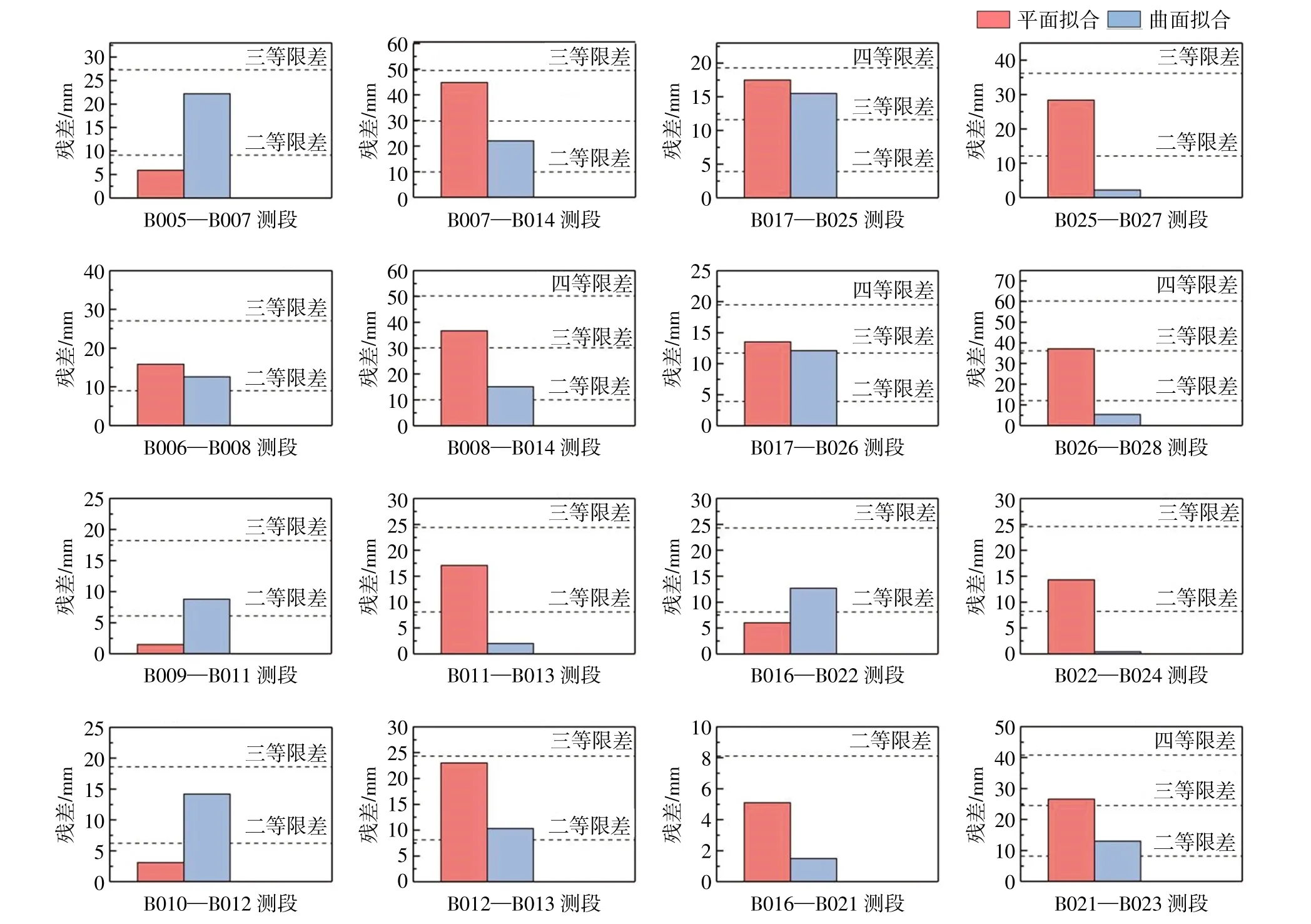
图6 跨海区域平面和曲面拟合内符合精度统计图
将拟合得到的跨海段1 和跨海段2 的拟合高差值与现有精密三角高程法结果作比对,见表7 和表8。
由表7 和表8 可得,跨海段1 和跨海段2 采用不同的拟合方法,所得高差值与原有精密三角高程法相比均满足三等水准检测限差要求(20),其中跨海段1 的直线和曲线拟合方法能满足二等水准检测限差要求(6)。值得注意的是,在线性拟合方法中,跨海段2 中内符合精度最高的三次曲线拟合高差值与原高差值的较差反而最大,其较差为-44.9 mm,且相较于其他结果有约6~8 cm 的高差差异,可能原因是B017—B025 测段间距太短引起的拟合突变。在平面拟合和曲面拟合中,跨海段1 的平面拟合高差值与原高差值较差更小,跨海段2 的曲面拟合高差值与原高差值较差更小。总体来看,采用高差拟合的方法能满足三等水准测量的精度要求,其中跨海段1 采用线性拟合的方法能达到二等水准测量的精度要求。

表7 高差拟合结果与精密三角高差法高差值统计表 单位:m

表8 高差拟合结果与精密三角高差法较差比对表 单位:mm
3 结 论
本次试验采用基于高程异常的GNSS 测量法,在陆地至上下川岛区域开展跨海段1(8.2 km)和跨海段2(12.6 km)的跨海高程传递,并与现有精密三角高程法结果进行比较,得到以下结论。
(1)采用常规的计算手段,在8.2 km 跨度的跨海段1 中,计算得到的高差值与现有高差值相比能达到二等水准测量精度。在12.6 km 跨度的跨海段2 中能达到三等水准测量精度。
(2)采用高差拟合的计算手段,拟合得到的2个跨海段高差值均能达到三等水准测量精度,其中对于10 km 以下的跨海段1 而言,采用线性拟合的方法能达到二等水准测量精度。
(3)GNSS 测量法可作为建立陆与岛、岛与岛间高程基准联系的高效手段,弥补了精密三角高程法受环境因素限制的不足,能为自然资源监测调查、海岸带地理信息工程、无人岛权属调查、深度基准建设以及应急测绘等项目提供高程服务。下一步将研究采用不同高精度重力场模型的移去—恢复法进行高差异常拟合,进一步提高该方法的跨海高程传递精度。
