基于SWAN 模式的波浪能发电装置输入能量计算方法研究

常 皓，王项南，张金凤，夏海南

（1.国家海洋技术中心，天津 300112；2.天津大学水利工程仿真与安全国家重点实验室，天津 300072）

近年来，随着传统能源的逐渐枯竭和海洋战略地位的日益凸显，具有清洁、可再生特点的海洋能的开发利用受到了世界各国政府的高度重视。2021年12 月，国务院批复同意了《“十四五”海洋经济发展规划》，提出了“优化海洋经济空间布局，加快构建现代海洋产业体系”的目标，其中“着力提升海洋科技自主创新能力，协调推进海洋资源保护与开发”成了我国重点规划内容之一，也是加快建设海洋强国的重要举措[1]。

波浪能是由海面吸收了风能后生成的波浪中所蕴含的一系列动能和势能的总称[2]，有着较高的能量密度，且相比于其他传统能源分布范围更广，因此是目前海洋能开发的主流方向之一。20 世纪以来，人类对波浪能的开发利用更是有了飞速的进展。国内外各种波浪能发电装置的研发也不断创新、层出不穷，出现了振荡水柱式、浮子式、蚌式、鹰式、摆式、鸭式等各种形式的装置[3]，但目前为止还没有一种装置在各方面均显示出绝对的优势。虽然各种装置在结构设计和发电原理上有所不同，但其功率特性、转换效率、可靠性等诸多因素仍然是当前波浪能发电装置研发、测试和改进的重点[4]。

在当下的评价体系中，针对波浪能发电装置进行一系列的测试与评价工作时，除了需要有效准确测试并计算装置输出端的电能外，输入能量的计算也同等重要，国际通用的测试标准中主要通过现场观测[5]来获取波浪参数，从而计算输入的波浪能，该方法不仅需要耗费极大的人力、物力和财力，而且可能由于观测工具误差、人为操作失误等原因导致现场观测存在一定误差，同时，现场环境的多变性也会影响现场观测数据的真实从而导致输入能量计算错误[6]。此外，国内外学者如张松等[7]、宗芳伊等[8]、SAKET A 等[9]、VICINANZA D 等[10]通过波浪数值模拟的方法获取高空间和时间分辨率的波浪参数，从而在勘测评估中计算当地的波浪能储备量。但往往得到的是大尺度、长期性的波浪能分布状况，仅适合进行发电装置的选点与波浪能评估工作，针对特定测试海域与时间范围内的待评价波浪能装置，无法对其输入波浪能进行精确计算。

本文基于该需求，研究了基于SWAN（Simulating Waves Nearshore）模式的波浪能发电装置输入能量计算方法，同时通过比较模型中不同参数对模拟结果的影响，并根据实测结果针对“长山号”发电装置选取了最佳模型设置，最终得到了装置所在位置的波浪参数并计算出输入波功率。

1 SWAN 海浪模式

第三代海浪模式SWAN 通过运用基于能量守恒原理的动谱平衡方程与线性随机表面重力波理论来构造数学波浪模型，该模式最先由荷兰的代尔夫特理工大学研发，经过多年的版本迭代后已经成为国际上常用的模拟风浪、涌浪及混合浪等的数值模型。此外，由于该模式能够同时考虑风输入、底摩阻、浅水变形、白浪耗散等多种因素，因此被广泛应用于河口、海岸等水域的波浪场模拟研究中。

1.1 基本控制方程

SWAN 模型采用波作用能量密度谱N（σ，θ）平衡方程来描述风生成浪的过程及波浪在近海区域的生长演化，平衡方程如式（1）所示。

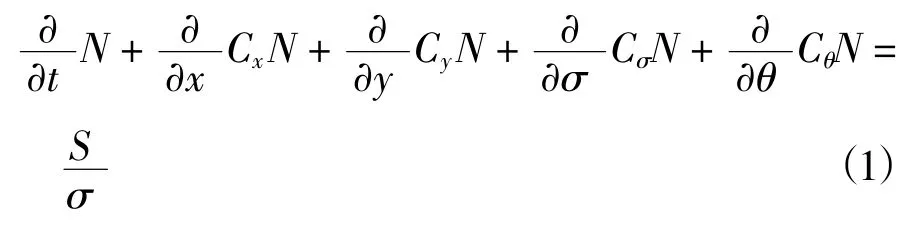
式中，Cx、Cy、Cσ和Cθ分别为风浪在位于地理空间的x、y 方向和σ、θ 空间上的传播速度；等式左侧各项分别表示谱密度由于水深变化和潮流作用引起的波谱密度在时间尺度与各个空间方向中的变化速率；等式右侧是该控制方程的源项，S（σ，θ）除包括风成浪的能量输入项外，还考虑了波浪传播过程中波浪能的耗散项，例如底摩擦、白浪耗散、水深变化、波浪破碎，以及波与波之间的非线性相互作用等相关因素[11]。

1.2 驱动风场

本文采用由CCMP（Cross Calibrated Multi-Platform）提供的海上10 m 的经向和纬向再分析风场数据作为SWAN 模型的驱动条件，其中CCMP 融合了多种卫星提供的风场数据与实测资料，该再分析风场涵盖了近乎全球范围（78.375°S—78.375°N，0.125°E—59.875°E，分辨率为0.25°），且所提供风场数据的时间间隔为6 h，相比于NCEP（National Centers for Environmental Prediction）、ERA（ECMWF Re-Analysis）等风场数据有更高的精确度，并且已经广泛应用在海洋、大气等领域的研究中[12-13]。

1.3 计算区域与参数设置

本文所研究的“长山号”500 kW 波浪能发电装置于2021 年4 月布放在广东省珠海市大万山岛海域，发电装置位置为（21°55.260′N，113°42.918′E），所在地水深约20 m。因此，本文计算区域设为中国南海，计算范围设为（11.5°N—25.5°N，105.5°E—120°E），模型东部和南部为开边界海域，大区域水深采用全球陆地海洋地形（ETOPO1）提供的分辨率为1′的大尺度水深数据，小区域水深同时参考了海图与实测数据，范围为（21.6°N—22.8°N，113.4°E—114.4°E）。

模型计算采用非结构化网格并在大万山岛海域加密，网格空间步长由开边界的15 km 逐渐过渡到装置所在附近的100 m 左右。SWAN 模型设置计算的时间步长为5 min，输出数据为每30 min 一次，输出参数包括：有效波高Hs、平均周期T1、谱峰周期Tp与平均波向Dir。初次模拟时将模型中底摩阻、波浪破碎指数、白浪耗散、三波四波相互作用等参数设为默认值，同时为研究各个参数对模拟结果的影响，采用控制变量法将模拟结果与仪器实测值进行对比，得到最适应该模型的SWAN 参数方案。

2 结果验证与优化

2.1 实测数据来源

国家海洋技术中心于2021 年5 月8 日至6 月8日对“长山号”波浪能发电装置进行了现场的波浪参数测试与电能测试，本次波浪测试采用的仪器为1 台波浪骑士浮标（以下简称波浪骑士）和2 台浪龙声学多普勒波浪流速剖面仪（以下简称浪龙），综合考虑测试海域的水深地形变化、波浪环境状况与测试对装置运行的影响，测试装置的位置分布如图1 所示。

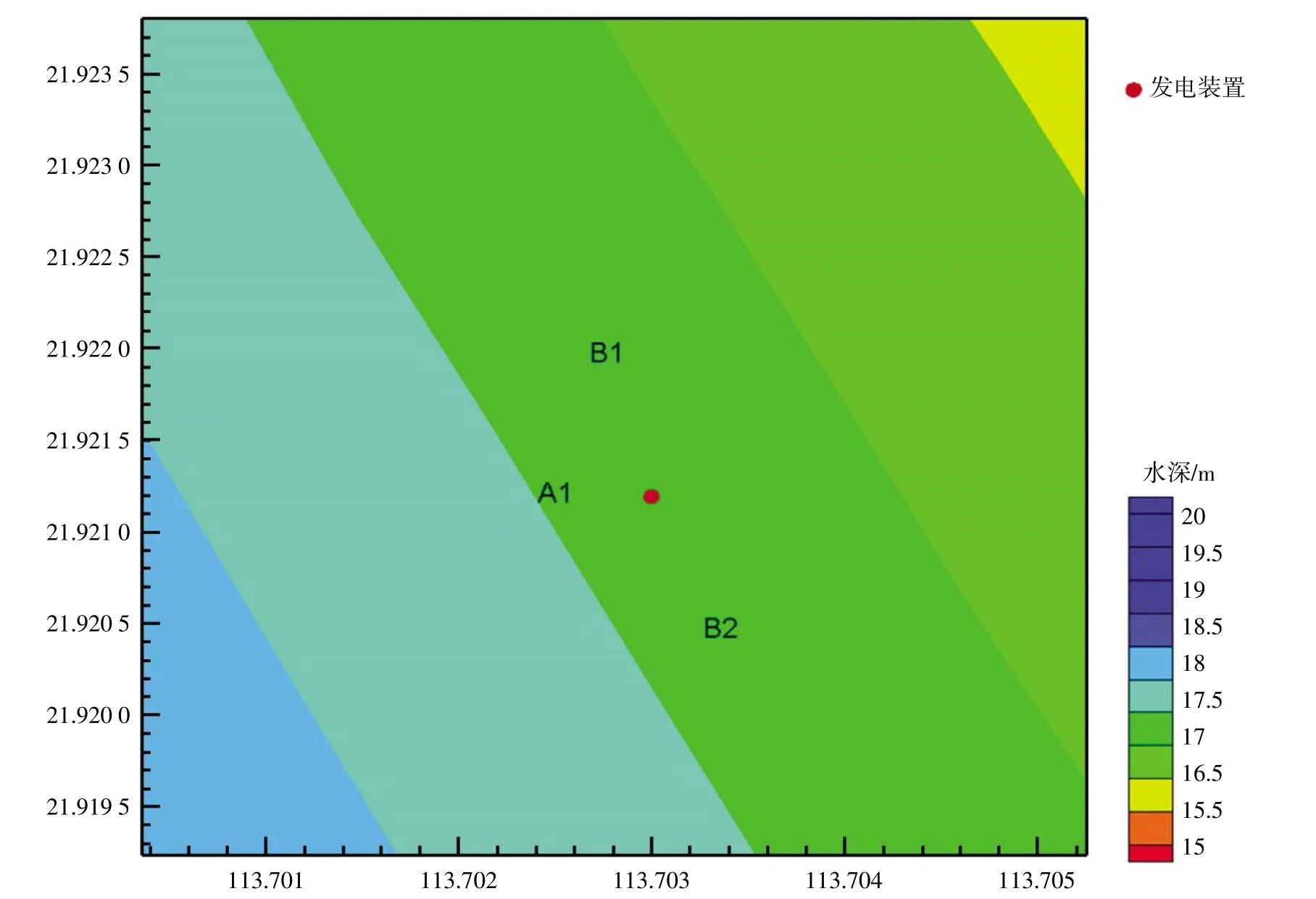
图1 装置与测点布置图

其中A1 为波浪骑士，布置在装置西侧100 m左右，且与来流方向基本平行以排除对流场的影响，B1、B2 为浪龙，分别放置在装置的东南与西北侧200 m 处以保持同一水深梯度。

在测试结束后，对装置进行回收并处理数据，将现场实测数据输出的波浪参数与模型同步为30 min。

2.2 模拟结果对比

由于研究测点区域距离地形边界足够远，因此采用冷启动方式直接引入CCMP 风场驱动模型，同时考虑到风浪生成对波浪模型的影响，在模拟时设置三天的预热时间以便风浪进行充分成长。

经过前期对比，由于3 台测试仪器的布置距离相对靠近，因此选择测点A1 波浪骑士所在位置的模拟与测试数据进行对比分析，并参考2 台浪龙的结果筛去不合格数据。在SWAN 模型的默认参数下，31 d 海试期间的模拟结果与实测值对比如图2和图3 所示，其中图2 表示有效波高的对比结果，图3 表示平均周期的对比结果。

图2 默认参数有效波高对比图

图3 默认参数平均周期对比图

由此可见，在采用CCMP 风场驱动，SWAN 模型保持默认参数的情况下，相比实测数据，模拟得到的有效波高与平均波周期数据均出现了偏小的情况，两者虽然变化趋势较为接近但差值明显。因此需要对模型的参数进行调整使得模拟结果更接近真实值。

2.3 参数优化

2.3.1 底摩阻对模拟结果的影响

底摩阻定义为当波浪自外海的深水区域向内海浅水区传播时，受到的近海底部介质产生的阻力作用。各国学者多年研究发现该过程中能量耗散主要包括3 个方面：底摩阻能量损失、渗流能量损失和泥面波能量损失。SWAN 中分别有经验性的JONSWAP 模式（默认）、拖曳模式COLLINS 和涡粘模式MADSEN 等底摩阻模式。

为研究不同底摩阻模式对SWAN 模型模拟结果的影响，本文选取了2021 年5 月18 日至5 月25日的风场数据进行波浪参数的模拟测试对比，波高与周期的对比结果如图4 所示。

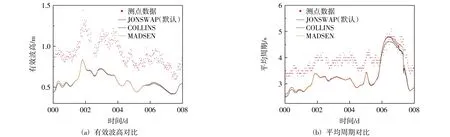
图4 底摩阻对模拟结果的影响

通过对比可知，3 种底摩阻模式的波高模拟值结果差别不明显，周期数据同样也仅在第6 天开始有显著差别。此外，通过调整各模式的底摩擦系数，可以发现虽然波高模拟值随底摩阻系数的减少而增大，但变化幅度有限，且3 种模式与实测结果仍有不小差距，优化后的模拟结果仍不太理想。

2.3.2 破碎指数对模拟结果的影响

众所周知，波浪由较深海域向浅水区传播时会引起相关的波浪变形，这种波浪变形积累到一定程度便会发生波浪破碎现象，波浪能在破碎过程中也会发生耗散。海底的地形条件是影响波浪破碎的重要指标之一，在模型中主要表现为破碎指数的不同。

波浪破碎能量耗散的公式如下。

式中，Sds，br为波浪破碎产生的能量耗散，E 为能量密度，且两者都是相对频率σ 与波向θ 的函数；Dtot代表单位面积上由于波浪破碎产生的能量耗散率；Etot代表波浪含有的总能量。

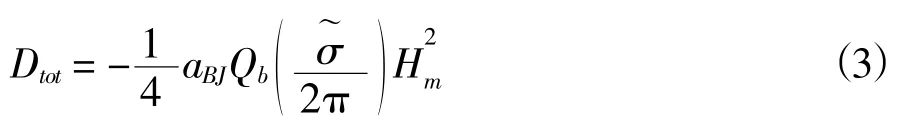
式中，αBJ为定常数1；Qb为波浪破碎因数；为平均频率。

式中，Hm为最大波高；d 为水深；r 为破碎指数。

参考KAMINSKY G M 等[14]的实验，除了SWAN的默认值0.73 外，本文还设置了从0.4～1.6，梯度为0.6 的3 组破碎指数进行模拟实验，波高与周期的对比结果如图5 所示。

图5 破碎指数对模拟结果的影响

从图中可以看出，在本次模拟的广东省珠海市大万山岛海域地形下，SWAN 模型对于破碎指数不敏感，即波浪破碎对于最终模拟的结果影响不大，不同方案下测点波高与周期相对于默认值均无较大差异。

2.3.3 非线性相互作用

SWAN 模式下不同波数间的非线性相互作用主要分为三波相互作用与四波相互作用两种，其分别在浅水区域和深水区域占有较高比重。本次研究海域为深水区域，因此，默认情况下模型中开启四波相互作用，另单设三波相互作用的情况与其对比，波高与周期的对比结果如图6 所示。

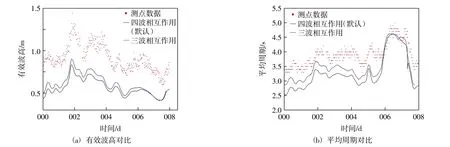
图6 非线性相互作用对模拟结果的影响

由于三波相互作用下，能量从低频向高频转移，因此出现了模拟结果偏高的情况，虽然模型在三波相互作用下的波高与周期均有一定程度增长，但相比实测值仍明显偏小。经过计算，四波相互作用下模拟波高与周期相对实测值的相关系数分别为0.880 和0.895；三波相互作用下则是0.891 与0.874，与四波对比没有明显改善，相对实测数据仍有较大差距，而且此次海测期间装置所在海域为深水区，因此本阶段继续选用四波相互作用。

2.3.4 风能输入与白浪耗散

SWAN 模式中风能输入分为线性增长项与指数增长项，其中线性增长项对波浪成长模拟结果的影响较小，而指数增长项主要有Komen 方案（默认）、Janssen 方案、Westhuysen 方案等，前两种方案目前运用较为主流。白浪耗散指的是当海浪发生破碎时，在破碎波波峰处产生的白色泡沫现象，因此，针对不同的风能输入方案也诞生了各自的白浪耗散形式[15]。

本文主要研究Komen 方案、Janssen 方案的风能指数增长项与其对应的白浪耗散模式。

（1）Komen 方案

Komen 方案下白浪耗散公式如式（5）和式（6）所示。

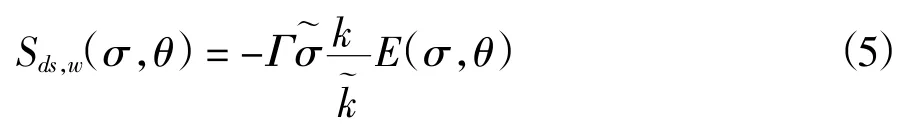
式中，Sds，w为白浪耗散造成的能量损失；σ~表示平均频率；表示平均波数；Γ 表示随波系数。

式中，Cds、δ、p 为可调参数；~为总波陡；为Pierson-Moskowitz 谱的s~值。

研究公式中参数变量Cds对模型的影响，默认值为2.36×10-5。为研究不同其取值对SWAN 模型模拟结果的影响，从1 × 10-6到2.36× 10-5选取了多组数值进行对比分析，调整该参数后的波高周期对比结果如图7 所示。

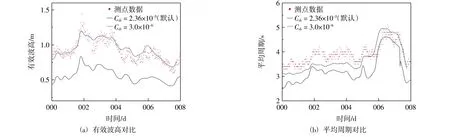
图7 Komen 方案模拟结果对比

可以看到随着破碎参数Cds的减少，有效波高和平均周期的数值模拟结果都有不同幅度的增长，且逐渐接近实测数据。通过参数对比实验，结果表明取Cds=3×10-6时模拟结果较为理想，并在变化趋势上与实测数据的一致性得到了显著提升。

（2） Janssen 方案

Janssen 方案下白浪耗散公式和Komen 方案中式（5）和式（6）相同，可调参数如下。

研究其中参数变量Cds1对模型的影响，其默认值为4.5，从0.5 到4.5（默认值）选取了多组取值进行对比分析。调整该参数的结果如图8 所示。

图8 Janssen 方案模拟结果对比

可以看到随着参数Cds1的减少，有效波高和平均周期的数值模拟结果都有不同幅度的增长，且逐渐接近实测数据。通过参数对比实验，结果表明Cds1=1.0 时，模拟结果较为理想。

（3）两方案对比分析

两种风输入指数增长和白浪耗散模式下，均通过参数对比实验取得了较理想的参数方案。为了定量分析两种方案对有效波高与平均周期模拟的影响，选取平均绝对误差MAE、平均相对误差MER均方根误差RMSE、相关系数r 来对比分析两方案与实测值之间的误差，两种方案下有效波高与平均周期的误差分别如表1 和表2 所示。、

表1 两种方案有效波高误差对比

表2 两种方案平均周期误差对比

通过对比，可以发现Janssen 方案的最佳参数设置下，模拟得到的有效波高与平均周期的误差相对较小且相关性更强，更符合现场实测的数值。

2.4 优化结果

运用改进后的参数方案进行波浪模拟计算，即底摩阻、破碎指数、非线性相互作用采用模型默认值，风能输入与白浪耗散项采用优化后的Janssen方案，针对波浪骑士31 d 测试期间有效波高与平均周期优化后的模拟结果与实测值对比如图9 和图10所示。

图9 优化方案有效波高对比图

图10 优化方案平均周期对比图

从图中可以看出，相较于模型默认设置，优化后的参数方案有效波高与周期模拟结果均有显著增长，图形与实测值的拟合程度也较好。表3 和表4也证明各项误差值对比优化前均有明显改进，相关性也得到了进一步加强，因此可以采用优化参数方案对大万山岛海域进行波浪数值模拟。

表3 优化前后有效波高误差对比

表4 优化前后平均周期误差对比

3 输入能量计算

3.1 波浪能公式

由于本次测试“长山号”所在海域为深水波（即水深大于二分之一波长时的波浪），采用简化后的波浪能功率密度公式如下。

式中，Pn为时间t 内的波浪能功率密度；ρ 为海水密度；Hs、Te分别为时间t 内的有效波高及对应的能量周期。

时间间隔t 内输入波功率Jn如下。

周期变换时参考黄必桂等[16]提出的经验公式如下。

式中，T1为平均周期。

3.2 输入波功率

从SWAN 数值模型中提取装置所在位置的波浪参数并将其代入式（8），可以得出每半个小时间隔的输入波功率，并将其整理为如图11 所示的波功率曲线。

图11 “长山号”输入波功率曲线

由此可以得到测试期间装置输入的平均波功率如下。

式中，N 为测试期间的时间间隔数。

4 结 论

本文基于SWAN 波浪模式，采用CCMP 风场驱动模型，构建了“长山号”波浪能发电装置所在广东省珠海市大万山岛海域的数值波浪场，将模拟结果与现场实测数据进行对比，结果表明优化后的SWAN 模型与测试结果具有较好的一致性，能较为合理地模拟海试期间大万山岛海域波浪场的有效波高与平均周期。

同时，通过控制变量法研究了SWAN 模式中各参数方案对模拟结果的影响，对比发现底摩阻、波浪破碎指数对波高与周期的影响有限，三波相互作用由于能使波能从低频向高频转移，因此出现了模拟结果偏高的情况，而结果对于风能输入与白浪耗散项更为敏感，最终通过误差分析发现Janssen 方案下，参数Cds1取1.0 时模拟结果较为理想。

最后，将模拟的有效波高与平均周期代入波浪能功率密度公式，计算得到了波功率曲线，并得到了海试期间的平均输入波功率。

下一步工作将根据“长山号”波浪能发电装置海试期间的电能测试数据，处理得到装置的输入能量，从而进行功率特性的分析并计算得到装置的能量转换效率，以便进一步对波浪能发电装置进行评价工作。