恒定流速下三角型沟槽隔水管减阻性能的仿真分析
2022-04-25何霞杨成宇王国荣钟林蒋雯婧
何霞,杨成宇,王国荣,钟林,蒋雯婧
恒定流速下三角型沟槽隔水管减阻性能的仿真分析
何霞a,b,杨成宇a,b,王国荣a,b,钟林a,b,蒋雯婧a,b
(西南石油大学 a.机电工程学院 b.能源装备研究院,成都 610500)
为了提高隔水管的使用寿命和保障深水钻井的安全性,在只考虑同一流速下的海流力、不同沟槽的布置对隔水管受力影响的工况下,利用织构减阻的原理,将三角型沟槽织构引入隔水管表面来起到降低隔水管绕流阻力的作用。采用大涡数值模拟,建立三角沟槽织构隔水管力学模型,在恒定流速下开展三角型沟槽深度和宽度几何参数对隔水管升阻力系数、速度场分布、压力系数分布、涡量分布影响规律的仿真分析,并与光滑隔水管的速度场分布、压力系数分布、速度矢量场分布进行对比。在南海恒定平均流速0.3 m/s的模拟工况下,当三角型沟槽织构沟槽个数为32时,沟槽织构隔水管的升阻力系数均小于光滑隔水管,起到了减阻抑升的作用,且在深度为0.14 mm、宽度为1.96 mm的条件下,隔水管的阻力系数降低了65.02%,升力系数均方根降低了78.3%,减阻效果最佳。建立了一套恒定流速下三角型沟槽隔水管绕流减阻优化设计与评价的新方法,为利用三角型沟槽织构改善隔水管的疲劳失效、提升其使用寿命提供了理论参考。
隔水管;三角型沟槽;涡激振动;大涡数值模拟;抑振减阻
随着海洋油气开发技术的提高,油气资源的勘采进入了更深的海域,高流速引起的漩涡泄放会加剧隔水管振动[1],加剧了隔水管的疲劳损伤。涡激振动抑制方法可以从三方面入手,分别是:通过改变质量、隔水管结构设计等方式重新设计隔水管参数;增加系统阻尼来提高隔水管系统的稳定性;添加附加抑制装置以减小振动。用于抑制海洋工程管柱涡激振动的方法,根据Zdravkovich[2]所做的研究可分为:管柱上表面突起物,可使得来流分离,扰乱尾部涡旋的线条装、螺旋列板、半球体凸面等;附加装置,如可将来流分离为许多小漩涡的多孔覆盖物、控制杆、轴向板条等;近尾流稳定装置,如导流板、分离盘、飘带等。
徐志辉[3]研究了国内螺旋列板,此装置的抑制原理是通过可改变沿管纵向的波流分离角,使得旋涡的强度被削弱,升力会降低,从而有效地弱化尾流涡旋,减小立管涡激振动响应[4]。但是螺旋列板材料的选择会因为密度增加管柱重量,并且安装成本较高,需要对其进行防腐处理[5]。许天羽等[6]运用CFD研究了导流板形横剖面立管对涡激振动的抑制,结果显示,导流板两侧角度选取的不同会产生不同的涡激抑制效果。赵恩金等[7]研究了导流板对海底管线涡激振动的影响,发现安装导流板会使管线分离点前移,并随着导流板的增高,周期性作用在管线上的竖直向下力逐渐增大。王晓龙等[8]研究了不同弦厚比、不同流速、不同直径立管的导流板对抑制涡激振动的影响规律,说明了导流板可以随来流方向旋转,在涡激振动的抑制方面高达80%,但是导流板结构设计和制作复杂,正常工作周期比螺旋列板更短,安装成本高。Roshko[9]在钝体尾流的研究文献中提出利用分离盘装置稳定管柱尾迹、抑制旋涡脱落。许博涵等[10]用风洞试验测试了柔性分离盘,结果显示,加装分离盘的长度为隔水管直径的0.5~2.5倍时,最大减阻效率可达30%。1987年Lesag等[11]通过在钝体上游放置控制杆减少其所受的拖曳力和横向力。Sakamoto等[12]研究了在圆柱系统内加控制杆来对流体力进行控制。Lee等[13]通过试验添加控制杆对圆柱所受拖曳力及其流场变化,添加控制杆使得圆柱的拖曳力系数最大可以减少29%,通过合理布置附属管线达到最大的减阻效果。通过对上述传统的涡激振动抑制装置调研发现其有效率的抑制涡激振动,针对不同的装置有各自的优缺点,但是传统的涡激振动抑制装置普遍具有安装难度大、结构更加复杂且成本较高的缺陷,不能适应各方向来流的海洋工况。
目前湍流边界层减阻的研究已经引起了国内外学者的高度重视。NASA兰利研究所发现顺流向微小的沟槽表面具有降低壁面摩阻的作用。学者们对此进行了不懈的探究,1999—2005年Yamagishi等[14-16]先后研究了在光滑圆柱表面周向布置不同深度的半圆沟槽、相同数量的深度半圆沟槽和三角沟槽及不同数量的三角形沟槽的流场情况,得出当沟槽数目为32时有较佳的减阻效果,且该三角形沟槽在特定雷诺数下具有高达30%的减阻效果。2004年Lim等[17]在光滑圆柱体表面布置了O型圆环,达到了控制尾流区旋涡脱落的目的,使得布置了O型圆环的圆柱受到的阻力减小。2013年Quintavalla等[18]通过试验研究了布置不同形状的沟槽的光滑圆柱的绕流情况,结果显示,沟槽使得临界雷诺数下降,具有较好的减阻效果。2018年王伟等[19]通过非定常数值研究方法对脊状结构表面圆柱的流场情况进行了研究,结果显示,在特定雷诺数下,阻力系数最大减少32.56%,升力系数最大减少65.41%。
传统的织构减阻常以平板为载体,将仿生织构运用到曲面(隔水管)的研究在国内开展得较少。故本文提出把三角型沟槽织构引入隔水管表面来降低绕流阻力的新方法,采用了大涡数值模拟方法,对25组布置有不同宽度与深度的三角沟槽的隔水管的流场进行分析,并与光滑隔水管流场参数进行对比,论证三角型沟槽对隔水管的减阻效果,为利用三角型沟槽织构改善隔水管的疲劳失效、提升其使用寿命提供理论参考。
1 数值计算方法
1.1 隔水管模型简化及三角沟槽建立
本文只考虑海流力、不同沟槽的布置及同一海洋流速对隔水管受力的影响。采用有限元法方法对隔水管进行分析,并假设:(1)隔水管单元体材料特性、几何特性均保持不变;(2)将隔水管上下端面简化为铰支约束的固定连接;(3)隔水管为刚性体,在自重和外力的作用下不发生形变,且不考虑隔水管内部钻柱及钻井液对其影响[20]。建立三角沟槽隔水管简化模型,如图1所示,其中沟槽数量为32,隔水管直径为=40 mm,展向长度=130 mm[21]。
隔水管所受雷诺数为2×104~8×105,由边界层公式(1)[22]计算得到边界层厚度为0.1~1 mm,式(1)中为边界层厚度,为隔水管展向长度,Re为展向长度为的隔水管所受的雷诺数,故选取5个深度(0.14、0.28、0.42、0.56、0.7 mm),并根据沟槽的间隙选择5个宽度(0.98、1.96、2.86、3.38、3.92 mm),如图2—3所示,并对以上参数进行正交数值仿真计算。试样代号如表1所示。
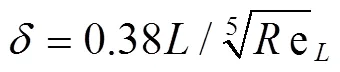
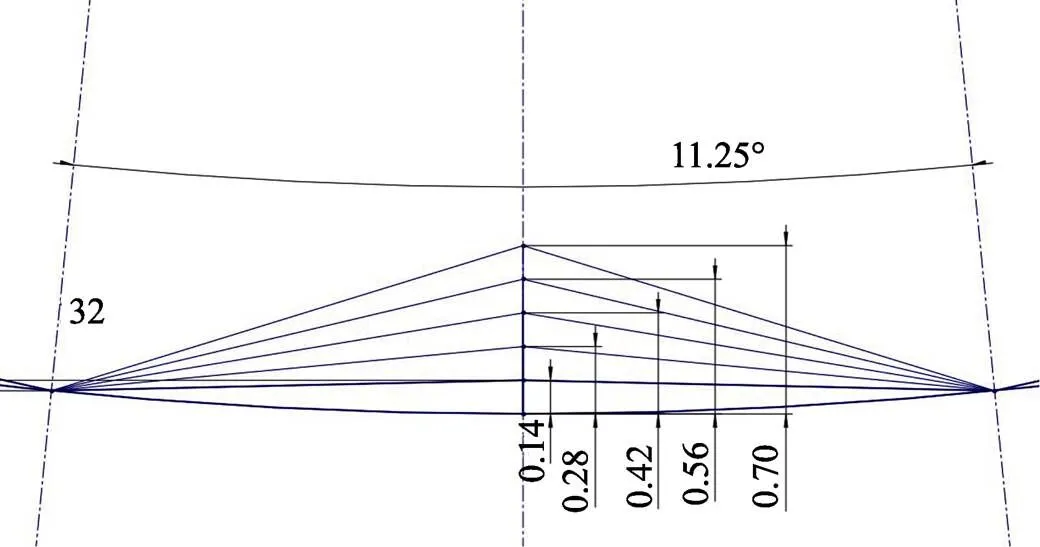
图2 三角沟槽深度的布置
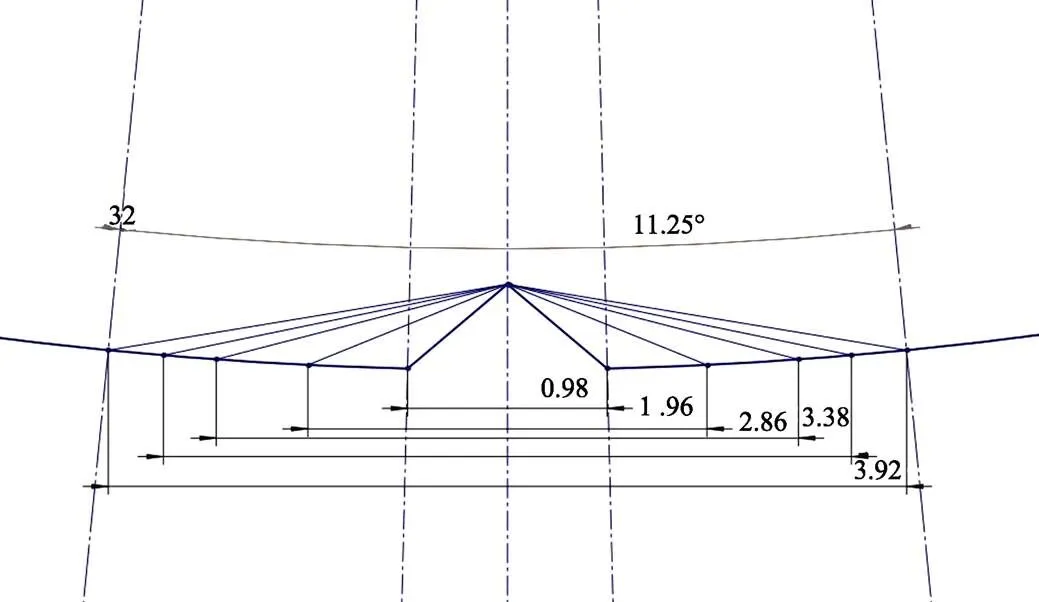
图3 三角沟槽宽度的布置
表1 不同宽度高度的正交计算
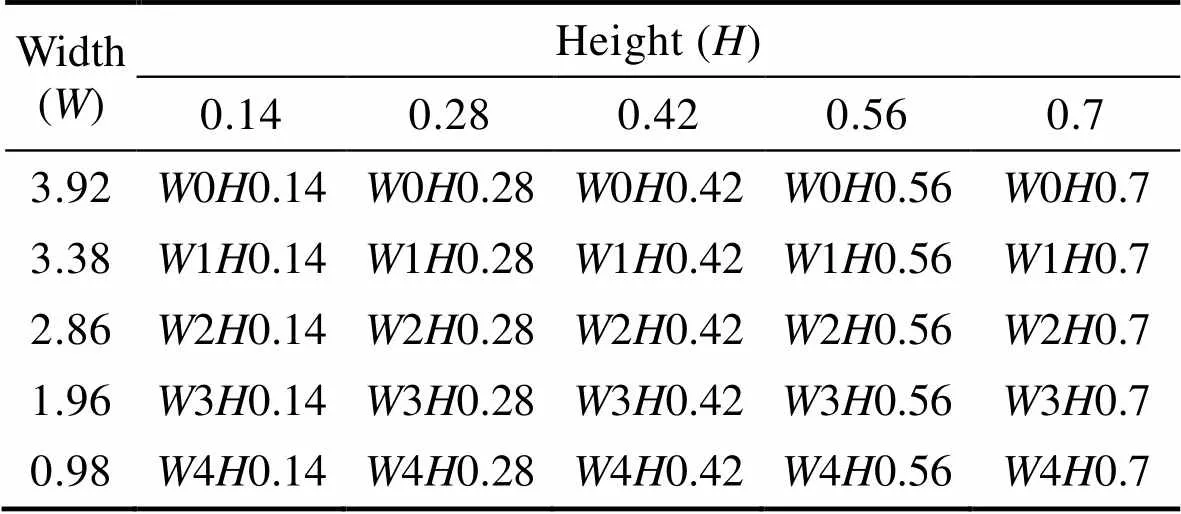
Tab.1 Orthogonal calculation of different width and height
1.2 控制方程与湍流模型
大涡数值模拟控制方程与Smagorinsky涡黏模型见公式(2)—(7)[23]。
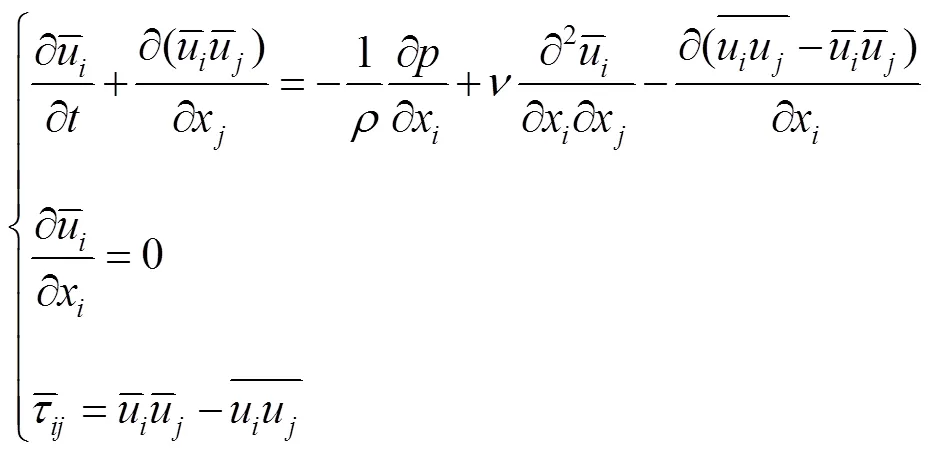
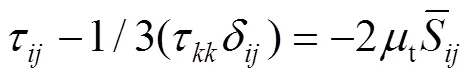
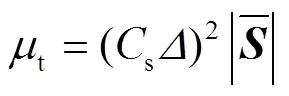
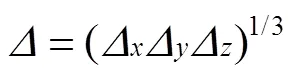
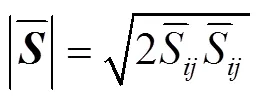
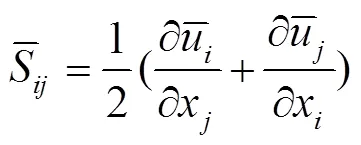
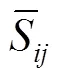
1.3 网格划分及边界条件
针对三角沟槽隔水管计算域,为保证本文大涡数值模拟方法的精确可靠性,计算域采用全局六面体网格,如图4—5所示,通过Fluent仿真软件,设置模拟时间为流体质点经过3~5倍计算域长度所需的时间。本模型中圆柱壁面边界层加密设置为40层,沿壁面法线方向与圆柱壁面相邻的块区域的边界层生长率为1.12,使得该网格满足壁面无量纲高度因子+=1,展示模型为20.42。

图4 W2H0.42三角沟槽全局网格

图5 W2H0.42三角沟槽隔水管近壁面网格
根据几何相似和雷诺相似的原理,在雷诺数相等的情况下,将数值带入公式(8),式中为流速,为密度(1 000 kg/m3),0为特征长度(此处对应隔水管的外径0),为动力黏度(=1.01×10‒3pa·s),0为南海海域平均流速(0=0.3 m/s)[17],0为附加浮力块的隔水管外径(0=0.7 m),通过计算得到雷诺数为2.1×105。本文光滑隔水管模型=40 mm,故在仿真计算中进口速度设置为=5 m/s。
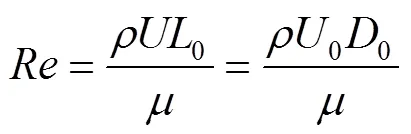
隔水管是柔性管柱,在海洋工况中承受梯度洋流,近海平面处流速较大且伴随有风浪冲击,流体冲击圆柱后无边界的自由扩散。故为了模拟海洋工况,设定左侧进口边界面(Inlet)为速度入口,速度方向沿着X轴,并在Z轴方向存在重力,使得流体自然流动;右侧出口边界(Outlet)面为自由出流,为压力出口且压力为0;除了左右两侧边界的其余四周边界面(Symmetry)均设定为对称壁面边界,且圆柱壁面(Wall)设定为固壁无滑移的边界条件,如图6所示,具体边界条件如表2所示。
表2 边界条件

Tab.2 Boundary conditions
2 沟槽隔水管的流场分析
2.1 升阻力系数
升阻力系数主要反映在该工况下沟槽隔水管瞬时受力行为特征,其表达式见式(9)—(10)[24]。
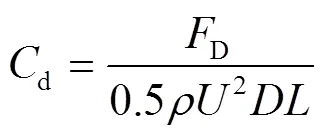
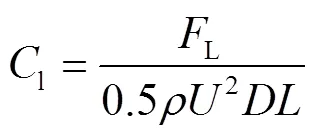
式中:d表示阻力,N;l表示升力,N;为海流密度,kg/m3;为圆柱体外径,m;为圆柱体展向长度,m。
如图7a所示,雷诺数=2.1×105时,光滑隔水管阻力系数为1.155,升力系数均方根为0.397[25]。在图7b—f中,所有沟槽隔水管的升阻力系数均小于光滑隔水管,说明三角沟槽织构对隔水管起到了减阻抑升的效果。在同一沟槽深度下,随着沟槽宽度的减小,阻力系数均存在先降后升的变化趋势;升力系数均方根在沟槽深度0.28 mm前后,分别呈现出先降后升、一直升高的变化趋势。由此可以说明,随着沟槽深度、宽度的增加,减阻效果降低,在沟槽深度为0.14 mm且宽度为0.98~1.96 mm时存在升阻力最小值,而减阻抑升效果最佳的点就在上述区间内。在25组数据中,沟槽30.14组的阻力系数为0.404、升力系数均方根为0.086,其减阻效率为65.02%,抑升效率为78.3%,减阻效果最佳;通过计算得到该组斯托鲁哈尔数=0.301,符合斯托哈尔数在粗糙圆柱面上的数值(0.1~0.47)[26],说明模拟结果是可靠的。在图7e和图7f中,有30.7、40.56、40.7 3个案例在计算过程中产生回流,最终导致计算终止。
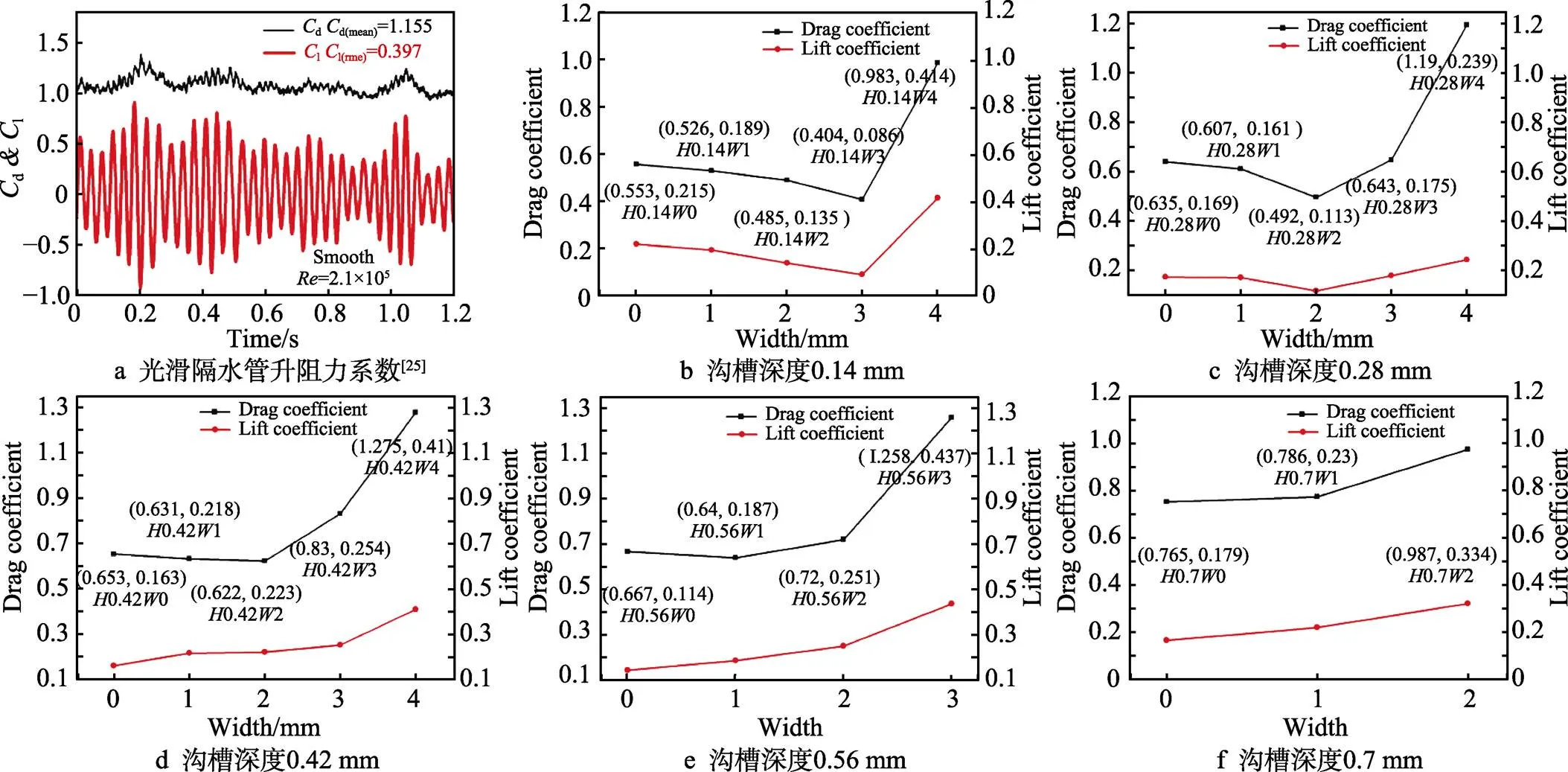
图7 光滑隔水管升阻力系数及沟槽隔水管升阻力系数的变化规律
2.2 速度与压力分布
由沟槽隔水管的升阻力系数分析可得,沟槽深度为0.14 mm时,减阻效果最显著,故对该深度下的沟槽隔水管进行速度场分析。从图8a—e可以看出,在同一沟槽深度0.14 mm下,随着沟槽宽度的减小,沟槽隔水管的尾流区域从沟槽壁面处分离时,位置逐渐向前移动,尾流区域沿来流法线方向上的宽度逐渐增大,且沿着来流方向的中心线上下交替排列,形成了规则、周期性的涡街排列,当宽度减少至0.42 mm后,尾流区域开始形成面积大而紊乱的速度分布区域。理论上阻力系数越小,克服阻力所损失的能量越少,对应的速度最大值应该增加[27]。从上文中的升阻力系数变化规律可知,前4组沟槽的升阻力系数依次逐渐减少。在图8中,前4组沟槽中沟槽壁面分离位置处向外的速度变化逐渐缓慢,能量损失逐渐减少,与升阻力系数的变化规律吻合,证明同一深度下沟槽隔水管的速度分布规律满足该原理。
由于第2组沟槽中,5组数据中20.28的升阻力系数最小,故比较同一宽度2.86 mm下不同沟槽深度的速度场分布情况。如图9a—e所示,随着沟槽深度的增加,尾流区域沿着来流的法线方向上的宽度逐渐增加,尾流区域从沟槽壁面分离时位置同样是逐渐向前移动,当深度增加至0.42 mm后,尾流区域开始形成面积大而紊乱的速度分布区域。由上文中升阻力系数变化规律可知,图9中5组沟槽的升阻力系数依次增大,在尾流区域没有出现紊乱的前2组沟槽速度分布的变化规律与升阻力变化规律吻合,也符合阻力系数越小,克服阻力所损失的能量越少的原理。
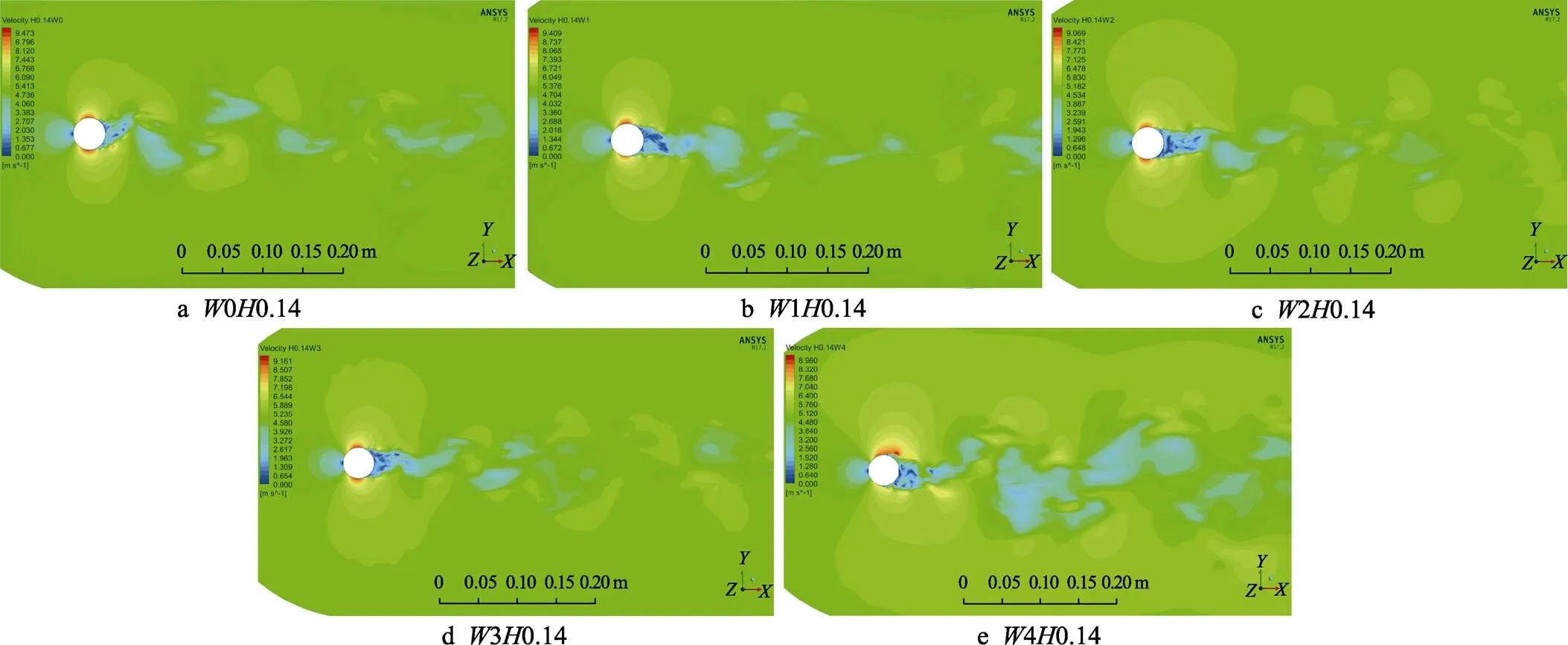
图8 沟槽深度为0.14 mm时不同宽度的速度分布云图
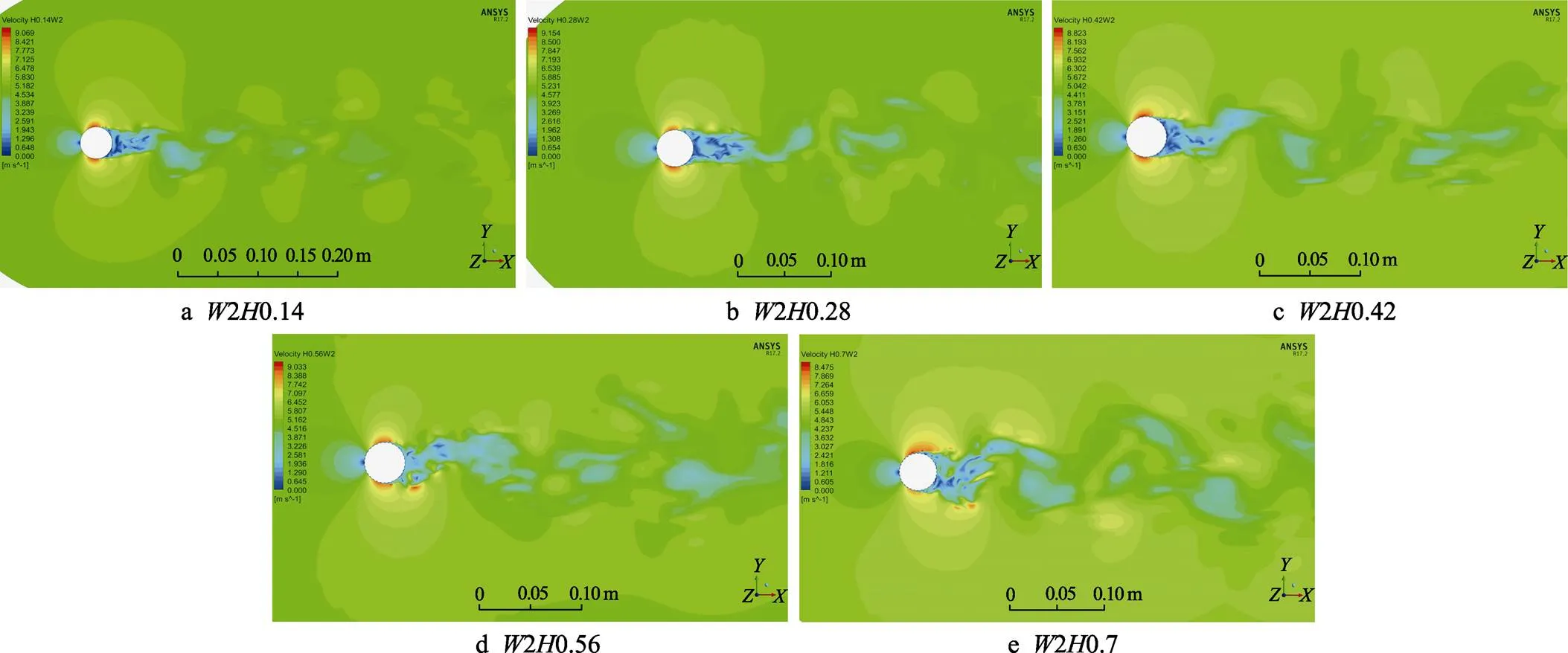
图9 沟槽宽度为2.86 mm时不同深度的速度分布云图
通过对不同宽度、深度的沟槽隔水管速度场分布分析可知,在上述沟槽深度、宽度的范围内,随着沟槽深度的减小、宽度的增加,尾流区域沿方向的宽度逐渐增加,尾流区域处的漩涡形成的涡街排列会更有规则性、周期性,减阻效果会更加明显。由于流体会在近壁面产生较大的速度梯度,当靠近壁面的速度在法线上的梯度为0时,会出现流动分离,且分离点越靠前,尾流区域越大[28],随着沟槽深度的增加、宽度的减小,沟槽织构会使流动分离点逐渐靠前。当沟槽深度大于0.42 mm、宽度小于0.98 mm时,尾流区域从沟槽壁面分离时的位置过于靠前,导致尾流区域将会出现大面积紊乱的速度分布区域,对隔水管的减阻起到负作用。
沟槽隔水管阻力减小的直接流场因素就是力的分布,压差产生的阻力是圆柱绕流流场中阻力产生的主要原因[29]。如图10所示,随着沟槽宽度的减小,前4组沟槽隔水管后方尾流区域的压力(压力分布云图上可通过颜色的深浅判断压力的变化规律)逐渐减小,前后的压差逐渐增大,阻力随之逐渐减小,而40.14组沟槽隔水管后方的压力急增,其前后的压差也急剧减少,阻力随之增加,与上文中同一深度0.14 mm、不同宽度的沟槽隔水管阻力系数的变化规律一致。
同样,探究同一宽度2.86 mm下不同沟槽深度的流场分布情况。由图11的压力云图分布可知,随着沟槽深度的增加,沟槽隔水管后方的尾流区域的压力逐渐减小,由最初的中压区域逐渐转变为尾流场的低压区压力分布,隔水管前后的压差也逐渐增大,阻力随之减小,与上文中同一宽度2.86 mm、不同深度的沟槽隔水管阻力系数的变化规律一致。图10—11所示压力分布云图中的压力均为静压。
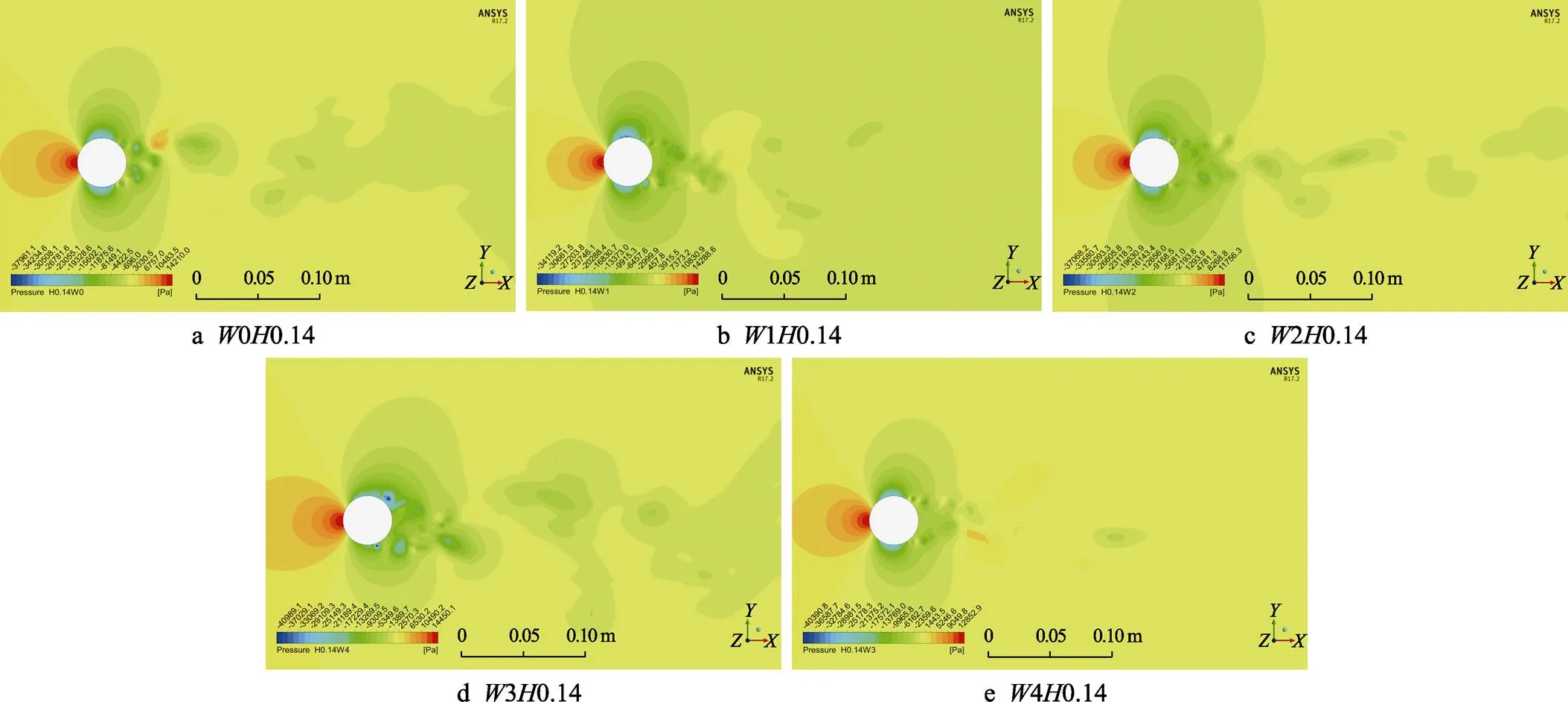
图10 沟槽深度为0.14 mm时不同宽度的压力分布云图
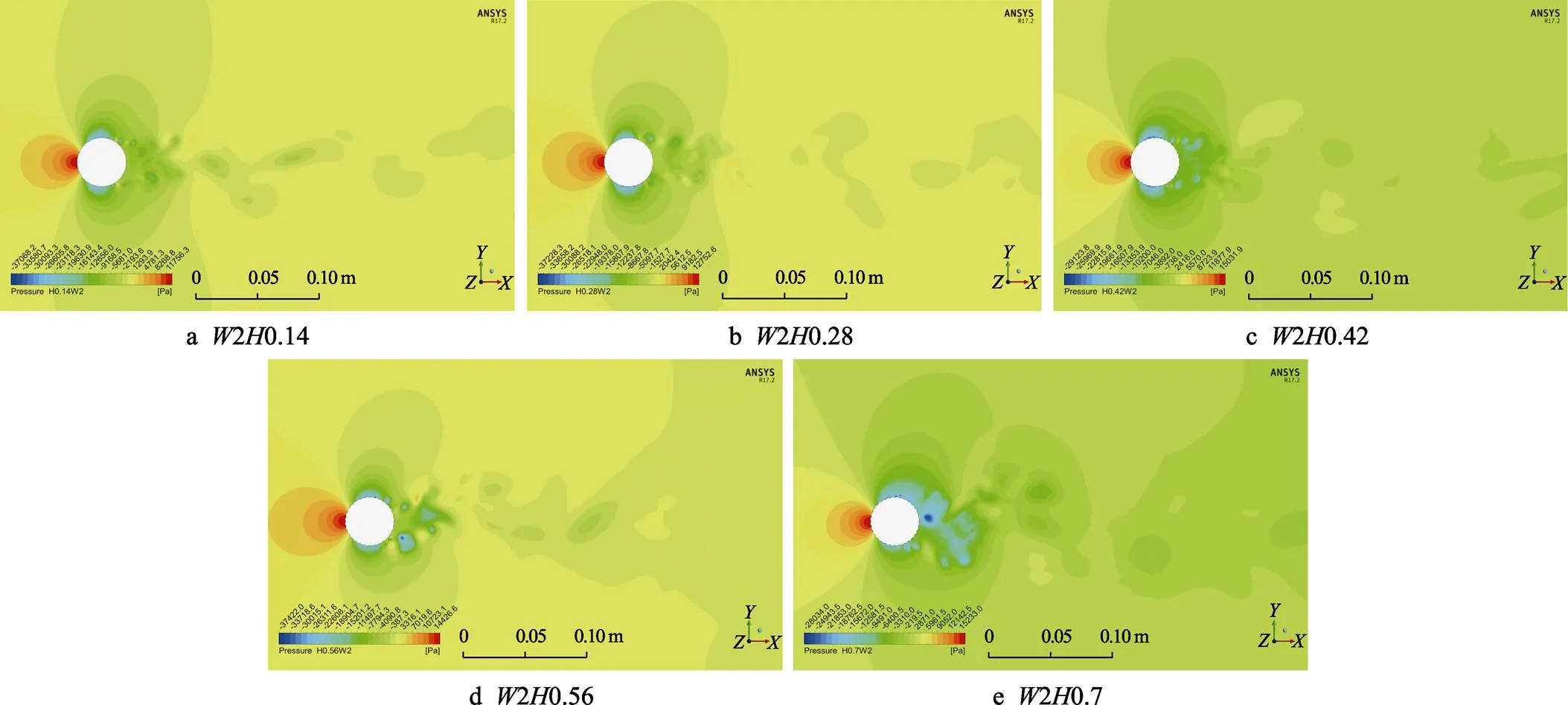
图11 沟槽宽度为2.86 mm时不同深度的速度分布云图
2.3 涡量分布规律
图12为第1组沟槽隔水管在=2.1×105时,=0时,圆柱中心截面上的涡量分布云图,从图中可以看出,沟槽尾流区域上下两侧涡量较大,形成交替脱落的漩涡,随着沟槽宽度的减小,漩涡脱落的频率增加,涡振漩涡强度增加且随着流体质点的流动逐渐减弱。由此可以看出,布置有沟槽结构的隔水管能够有效改变其尾流的漩涡脱落频率,改变沟槽隔水管的振荡频率,降低涡激振动对隔水管的疲劳损坏。
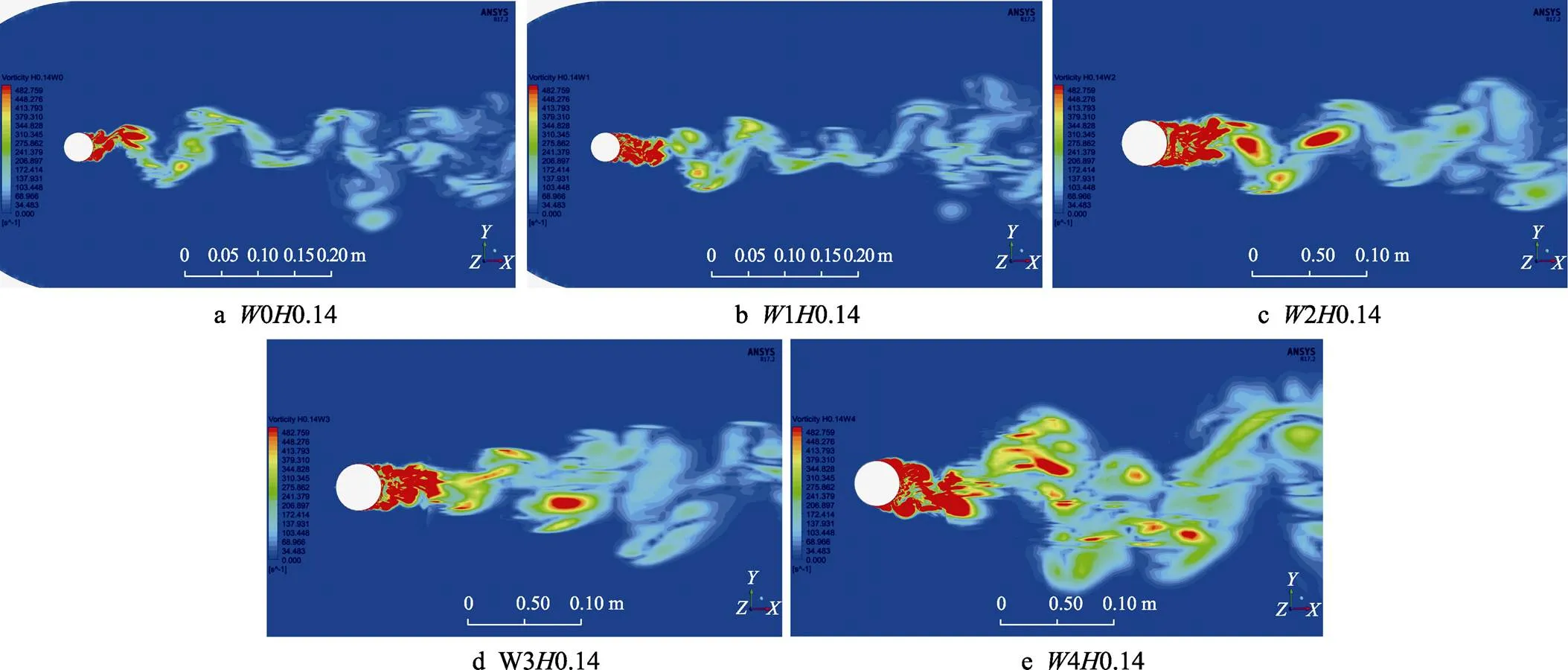
图12 深度为0.14 mm时不同宽度的沟槽隔水管涡量分布云图
3 三角沟槽减阻效果的评价
对不同参数的沟槽隔水管的分析可以得出,在此25组的织构布置中,30.14是减阻抑升性能最佳的沟槽布置,下面将对光滑隔水管和30.14的流场各物理量进行分析,进一步判断沟槽的布置对哪些因素造成了影响。
从图13可以看出,在隔水管上布置了沟槽的结构体速度的最大值更大、压力值更小,说明动能向压力能的转换量减小,尾流近壁面速度存在接近于0的点,速度为0的区域是由于漩涡的脱落造成大涡破碎成小涡,从而将动量传递和消耗;光滑隔水管的尾流区域呈现放射状的放大趋势,而沟槽隔水管的尾流区域呈现收缩状,也可以看出沟槽隔水管尾迹区域的宽度明显减小,且沟槽隔水管速度回流的区域沿着流体质点运动方向向后移动,速度分离点向后移动了约23°,说明该沟槽结构能够控制尾流区域达到延缓流动分离的目的。
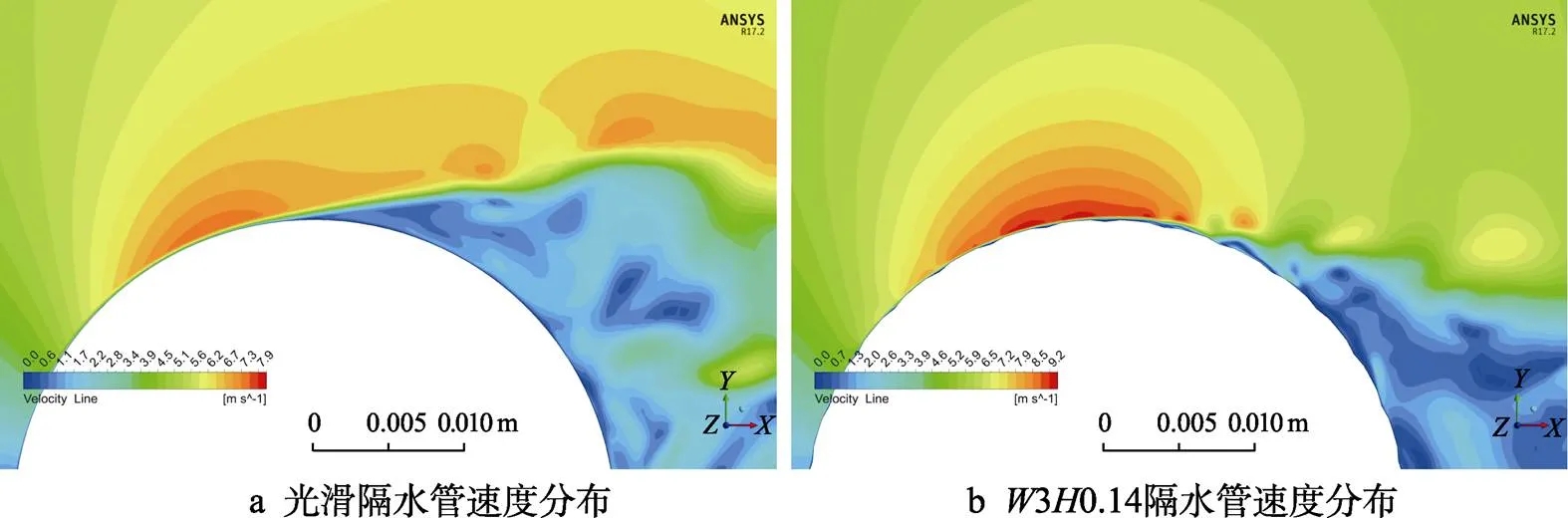
图13 速度分布对比图
图14可以从颜色数值大小的分布来分析,首先光滑隔水管的最小压力系数为‒2.5,沟槽隔水管的最小压力系数为‒4,最小压力值出现在隔水管两侧的上下端面,说明沟槽隔水管两侧速度更大,保留的动能更多;光滑隔水管的较小压力数值为‒2.2~ ‒0.8,大面积地出现在尾流区域,而沟槽隔水管的尾流区的较小压力数值为‒1.6~0。在尾流区域沟槽隔水管的压力明显大于光滑隔水管,使得沟槽隔水管的前后压差远远小于光滑隔水管,压差阻力是造成隔水管横向振动和变形大位移的主要原因,压差阻力越小,横向振动越小,隔水管变形也越小。
在图15所示的速度矢量图中加入速度流线,流线代表流体质点在隔水管中心面=0的轨迹,光滑隔水管上红色矩形框内的速度近似为0,光滑隔水管的分离点在90°左右;而沟槽隔水管在90°之后的壁面上发生了明显的分离再附现象,漩涡产生的位置明显向后移动,而分离点也向后移动,且前者流线的流向是放开向外,沿着隔水管壁面呈放大的趋势,后者的流线沿着隔水管90°切线方向向=0的中心线偏移,呈现收口的趋势,说明尾流区域沟槽隔水管的速度小于光滑隔水管。
综上可知,在速度分布上沟槽隔水管的最大速度更大,压力最小值更小,沟槽隔水管尾流区的再附现象和二次分离点沿着流动方向向后延伸,三角沟槽壁面增加了边界层的扰动,使得沟槽凹槽内形成了旋转的漩涡。该漩涡方向与流体流动方向相反,沟槽凸起处呈现较低的流速,将流动分离点延后,使沟槽隔水管的尾流区域更小,压差阻力也更小,使得整体的升力阻力得到控制,起到了抑升减阻的效果。
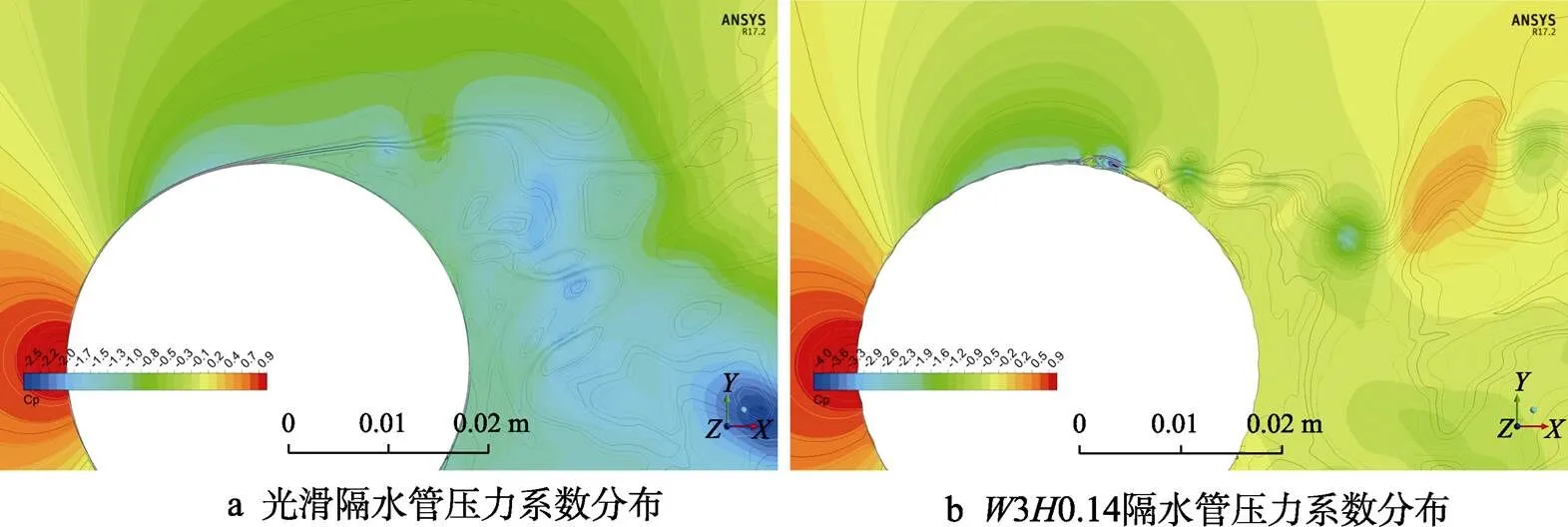
图14 压力系数分布对比图
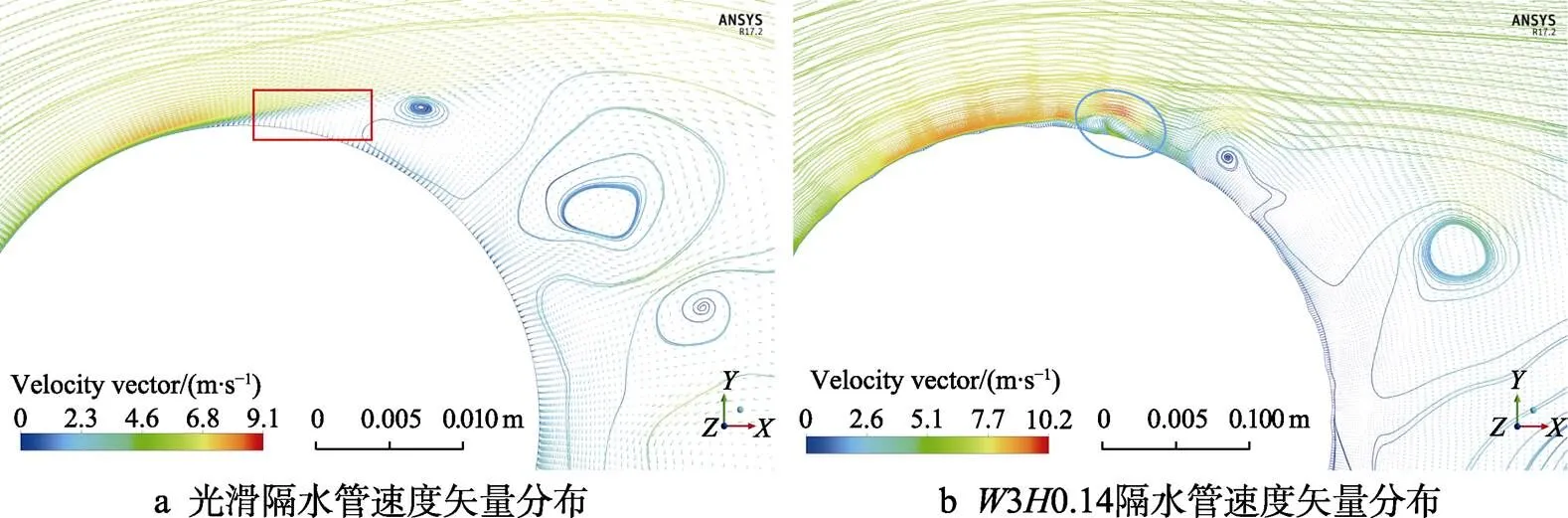
图15 隔水管速度矢量对比图
4 结论
1)建立了三角沟槽织构隔水管大涡数值模拟模型,整体模型采用全局六面体网格,并进行了网格无关性验证,使得该网格满足壁面无量纲高度因子+=1,保证网格的精度,为利用三角型沟槽织构改善隔水管的疲劳失效、提升其使用寿命提供了理论参考。
2)采用大涡数值模拟方法,开展了5种深度和5种宽度沟槽布置的隔水管升阻力系数数值计算,得到了在=2.1×105时,随着沟槽深度的增加,阻力系数逐渐增大。在选取的25组数据中,30.14在升阻力系数的大小上表现最好,并随着沟槽宽度的减小,升阻力系数呈现先减小再增大的趋势。与光滑隔水管的升阻力系数数值对比,其阻力系数降低了65.02%,升力系数均方根值降低了78.3%,这种沟槽的布置大大减小了隔水管上所受的阻力与升力。
3)光滑隔水管与30.14沟槽隔水管的对比结果显示,在30.14沟槽隔水管的布置时,速度场变大,隔水管尾流区的压力显著增大,前后压差减小导致压差阻力减小。对比光滑隔水管,沟槽隔水管的分离点靠后,尾流区域的宽度大大减小,进一步证实了沟槽织构布置在隔水管上起到了减阻抑升的可行性。
[1] 梁健, 刘成文, 李兆敏. 带整流罩隔水管流场特性的大涡模拟研究[J]. 力学季刊, 2020, 41(1): 197-205.
LIANG Jian, LIU Cheng-wen, LI Zhao-min. Large Eddy Simulation Study on Flow Field Characteristics of Risers with Fairings[J]. Chinese Quarterly of Mechanics, 2020, 41(1): 197-205.
[2] ZDRAVKOVICH M M. Review and Classification of Various Aerodynamic and Hydrodynamic Means for Suppressing Vortex Shedding[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1981, 7(2): 145-189.
[3] 徐志辉. 螺旋列板在海底管道上的国产化应用[J]. 化工设计通讯, 2017, 43(4): 167-168.
XU Zhi-hui. Localization of Spiral Plate in Submarine Pipeline[J]. Chemical Engineering Design Communications, 2017, 43(4): 167-168.
[4] 杨加栋, 张晓灵, 杜宝银, 等. 螺旋列板——深水立管涡激振动抑制装置[J]. 海洋技术, 2010, 29(4): 88-92, 116.
YANG Jia-dong, ZHANG Xiao-ling, DU Bao-yin, et al. Helical Stakes—Vortex Induced Vibration Suppression Devices of Deepwater Risers[J]. Ocean Technology, 2010, 29(4): 88-92, 116.
[5] 郑斌, 袁巨龙, 赵萍, 等. 变曲率沟槽精密球研磨加工优化实验研究[J]. 表面技术, 2017, 46(2): 214-219.
ZHENG Bin, YUAN Ju-long, ZHAO Ping, et al. Experiment of Optimized Grinding of Precision Ball with Variable-radius Groove[J]. Surface Technology, 2017, 46(2): 214-219.
[6] 许天羽, 郑婷婷, 胡建新. 基于CFD的导流板形海洋立管涡激抑制研究[J]. 浙江海洋学院学报(自然科学版), 2011, 30(6): 533-537.
XU Tian-yu, ZHENG Ting-ting, HU Jian-xin. Study on Vortex Suppression of Guide-Vane Style Riser in Ocean Current Based CFD[J]. Journal of Zhejiang Ocean University (Natural Science), 2011, 30(6): 533-537.
[7] 赵恩金, 拾兵, 曹坤. 导流板对海底管线涡激振动的影响[J]. 哈尔滨工程大学学报, 2016, 37(3): 320-325.
ZHAO En-jin, SHI Bing, CAO Kun. Influence of Reflectors on Vortex-Induced Vibration of Subsea Pipelines[J]. Journal of Harbin Engineering University, 2016, 37(3): 320-325.
[8] 王晓龙, 王刻强, 胡成. 导流板涡激振动抑制模拟分析[J]. 辽宁化工, 2019, 48(11): 1115-1118.
WANG Xiao-long, WANG Ke-qiang, HU Cheng. Simulation Analysis on Vortex-Induced Vibration Suppression of Guide Plate[J]. Liaoning Chemical Industry, 2019, 48(11): 1115-1118.
[9] ROSHKO A. On the Wake and Drag of Bluff Bodies[J]. Journal of the Aeronautical Sciences, 1955, 22(2): 124-132.
[10] 许博涵, 王嘉松, 梁盛平. 柔性分离盘抑制圆柱涡激振动的风洞试验[J]. 水动力学研究与进展(A辑), 2017, 32(4): 470-476.
XU Bo-han, WANG Jia-song, LIANG Sheng-ping. Wind Tunnel Experiment of VIV Control on Circular Cylinder with Flexible Splitter Plate[J]. Chinese Journal of Hydrodynamics, 2017, 32(4): 470-476.
[11] LESAGE F, GARTSHORE I S. A Method of Reducing Drag and Fluctuating Side Force on Bluff Bodies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1987, 25(2): 229-245.
[12] SAKAMOTO H, HANIU H. Optimum Suppression of Fluid Forces Acting on a Circular Cylinder[J]. Journal of Fluids Engineering, 1994, 116(2): 221-227.
[13] LEE S J, LEE S I, PARK C W. Reducing the Drag on a Circular Cylinder by Upstream Installation of a Small Control Rod[J]. Fluid Dynamics Research, 2004, 34(4): 233-250.
[14] YAMAGISHI Y, OKI M. Effect of the Number of Grooves on Flow Characteristics around a Circular Cylinderwith Triangular Grooves[J]. Journal of Visualization, 2005, 8(1): 57-64.
[15] SATO R, KOGANEI N, YAMAGISHI Y, et al. Effect of Groove Shape on Fluid Flow around a Circular Cylinder with Grooves[J]. Journal of the Visualization Society of Japan, 2008, 28-1(2): 1029.
[16] OKI M, AOKI K, NAKAYAMA Y. Effect of Grooves’ Depth for Flow Characteristics around a Circular Cylinder with Grooves[J]. Transactions of the Japan Society of Mechanical Engineers Series B, 1999, 65(631): 870-875.
[17] LIM H C, LEE S J. Flow Control of a Circular Cylinder with O-Rings[J]. Fluid Dynamics Research, 2004, 35(2): 107-122.
[18] QUINTAVALLA S J, ANGILELLA A J, SMITS A J. Drag Reduction on Grooved Cylinders in the Critical Reynolds Number Regime[J]. Experimental Thermal and Fluid Science, 2013, 48: 15-18.
[19] 王伟, 宋保维, 毛昭勇, 等. 脊状结构表面圆柱绕流的流体特性研究[J]. 华中科技大学学报(自然科学版), 2018, 46(9): 107-111.
WANG Wei, SONG Bao-wei, MAO Zhao-yong, et al. Study on Hydrodynamic Characteristics of Flow around a Cylinder with Ridged Surface Structure[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2018, 46(9): 107-111.
[20] 刘清友, 周守为, 姜伟, 等. 基于钻井工况和海洋环境耦合作用下的隔水管动力学模型[J]. 天然气工业, 2013, 33(12): 6-12.
LIU Qing-you, ZHOU Shou-wei, JIANG Wei, et al. A Dynamic Model of Marine Risers/Pipes under the Drilling Operation Condition and Sea Environment[J]. Natural Gas Industry, 2013, 33(12): 6-12.
[21] 蒋雯婧, 钱权, 王国荣. V型沟槽表面隔水管减阻的大涡数值模拟研究[C]//第十届全国流体力学学术会议. 杭州: 中国力学学会, 2018: 355.
JIANG Wen-jing, QIAN Quan, WANG Guo-rong. Large Eddy Numerical Simulation Research on Drag Reduction of V-Groove Surface riser[C]//Abstracts of Papers of the Tenth National Symposium on Fluid Mechanics. Hangzhou: Chinese society of mechanics, 2018: 355.
[22] 宫武旗, 李新宏, 黄淑娟. 沟槽壁面减阻机理实验研究[J]. 工程热物理学报, 2002, 23(5): 579-582.
GONG Wu-qi, LI Xin-hong, HUANG Shu-juan. Experiment Study on the Mechanism of Riblets Drag Reduction[J]. Journal of Engineering Thermophysics, 2002, 23(5): 579-582.
[23] 李启. 含运动边界钝体绕流风场的大涡模拟数值算法[D]. 北京: 北京交通大学, 2014.
LI Qi. A Numerical Method for Large-Eddy Simulation of the Wind Field around a Bluff Body with Moving Boudaries[D]. Beijing: Beijing Jiaotong University, 2014.
[24] 陈进娥, 何顺利, 刘广峰. 我国海洋石油勘探开发装备现状及发展趋势[J]. 油气藏评价与开发, 2012, 2(6): 67-71.
CHEN Jin-e, HE Shun-li, LIU Guang-feng. Current Situation and Development Trends of China Offshore Oil Exploration and Development Equipments[J]. Reservoir Evaluation and Development, 2012, 2(6): 67-71.
[25] 钱权. 典型沟槽表面隔水管减阻性能研究[D]. 成都: 西南石油大学, 2018.
QIAN Quan. Research on Drag Reduction Performance of Riser on Typical Grooved Surface[D]. Chengdu: Southwest Petroleum University, 2018.
[26] Strouhal V. Uber Eine Besondere Art Der Tonerregung[J]. Annalen Der Physic, 1878, 6: 216-251.
[27] 何霞, 蒋雯婧, 王国荣, 等. 基于大涡数值模拟的海洋隔水管绕流分析[J]. 水动力学研究与进展(A辑), 2020, 35(1): 106-112.
HE Xia, JIANG Wen-jing, WANG Guo-rong, et al. Flow around Analysis of Riser Based on Large Eddy Numerical Simulation[J]. Chinese Journal of Hydrodynamics, 2020, 35(1): 106-112.
[28] 田启龙, 黄熙龙, 王嘉松. 附加附属管的隔水管涡激振动离散涡模拟[J]. 水动力学研究与进展(A辑), 2016, 31(5): 633-640.
TIAN Qi-long, HUANG Xi-long, WANG Jia-song. Vortex- Induced Vibration of the Riser with Affiliated Pipes Based on Discrete Vortex Method[J]. Chinese Journal of Hydrodynamics, 2016, 31(5): 633-640.
[29] 邓欣, 朱赛健, 李保军, 等. 隔水管尾流误差补偿技术研究[J]. 国外电子测量技术, 2016, 35(8): 42-44, 50.
DENG Xin, ZHU Sai-jian, LI Bao-jun, et al. Research of Error Compensation for Riser Wake[J]. Foreign Electronic Measurement Technology, 2016, 35(8): 42-44, 50.
Simulation Analysis of the Drag Reduction Performance of Triangular Groove Riser under Constant Flow Velocity
a,b,a,b,a,b,a,b,a,b
(a. College of Electromechanical Engineering, b. Energy Equipment Research Institute, Southwest Petroleum University, Chengdu 610500, China)
In order to improve the service life of the riser and ensure the safety of deep-water drilling, under the condition that only the marine current force at the same velocity and the influence of different groove arrangement on the stress of the riser are considered, the triangular groove texture is introduced into the riser surface to reduce the flow resistance of the riser by using the principle of texture drag reduction. Using large eddy numerical simulation, the mechanical model of triangular groove textured riser is established. The effects of geometric parameters of triangular groove depth and width on riser lift resistance coefficient, velocity field distribution, pressure coefficient distribution and vorticity distribution are simulated and analyzed at constant velocity. The velocity vector field distribution is compared.The results show that under the simulated condition of constant average velocity of 0.3 m/s in the South China Sea, when the number of triangular groove texture grooves is 32, the rise resistance coefficient of grooved texture riser is less than that of smooth riser, which plays the role of reducing resistance and restraining rise. When the depth is 0.14 mm and the width is 1.96 mm, the resistance coefficient of riser is reduced by 65.02% and the root mean square of lift coefficient is reduced by 78.3%. The drag reduction effect is the best. Based on this, a new method for optimal design and evaluation of flow drag reduction around triangular grooved riser at constant flow velocity is established, which provides a theoretical reference for improving the fatigue failure and service life of riser by using triangular grooved texture.
riser; triangular groove; vortex-induced vibration; large eddy numerical simulation; vibration suppression and drag reduction
TH117
A
1001-3660(2022)04-0157-10
10.16490/j.cnki.issn.1001-3660.2022.04.015
2021-03-23;
2021-10-21
2021-03-23;
2021-10-21
何霞(1976—),女,博士,副教授,主要研究方向为油气装备润滑减磨。
HE Xia (1976—), Female, Doctor, Associate professor, Research focus: lubrication and wear reduction of oil and gas equipment.
王国荣(1977—),男,博士,教授,主要研究方向为天然气水合物开采工艺及能源装备。
WANG Guo-rong (1977—), Male, Doctor, Professor, Research focus: natural gas hydrate mining technology and energy equipment.
何霞, 杨成宇, 王国荣, 等. 恒定流速下三角型沟槽隔水管减阻性能的仿真分析[J]. 表面技术, 2022, 51(4): 157-166.
HE Xia, YANG Cheng-yu, WANG Guo-rong, et al. Simulation Analysis of the Drag Reduction Performance of Triangular Groove Riser under Constant Flow Velocity[J]. Surface Technology, 2022, 51(4): 157-166.
责任编辑:万长清
