公共卫生事件下个人防护用品储备指标数及最优储备量研究

荣一臻

（湘潭大学 公共管理学院，湖南 湘潭 411105）

一、问题的提出

突发性的公共卫生事件是全球都在面临的共同挑战，长期以来各国都在积极寻求应对突发公共卫生事件的办法。个人防护用品（Personal Protective Equipment）以下简称PPE是突发公共卫生事件爆发时最重要的应急物资。国家和政府合理的PPE储备是有效响应和应对公共卫生事件的有力保证。一个国家或者地区PPE的合理储备，可以为当地突发性公共卫生事件的迅速传播提供有效阻断。然而，面对同时在全国乃至全世界范围内暴发的突发性公共卫生事件，不同省、市、县级地区所需的PPE数量也不完全相同，这也给PPE的合理储备造成了一定程度的困难。而造成这种需求差别的最直接的影响因素是一个省、市、县级地区的医务从业人员人数、经济发展程度和地区总人口数①。一个地区医务从业人员数量越多，在公共卫生事件爆发时，所需的PPE数量就越多，需要救治的人数也随地区人口数量变化，人口密度的变大，传播的速度和范围可能越广②。若是在没有及时有效的PPE供给情况下，公共卫生事件传播的不利影响及其相互叠加和放大的影响就越强，PPE供给的紧迫性和重要性也就越大③。那么加快建成省级的医疗物资储备体系，以适度的规模、合理的结构、科学的管理和高效的运作，确保在发生重大公共卫生事件后，人们能够获得极为关键的医疗救治和必要的应急物资正分重要①。

近年来，为了解决应急物资实物储备的弊端，国内外学者已开始了大量研究。如董骏峰为了稳步提升应急物资的满意度,并且在一定范围内减少运输和仓储成本,通过构建物资储备数学模型,结合NSGA-II算法和动态KNN算法对该模型进行最优值求解,并最终获得了最佳的应急物资储备计划④。蒲宇建立了基于改进的模糊Petri网的应急能力评估模型，并以某市级救灾物资仓库为例进行了案例分析，提出相应的对策和建议，从新的视角对救灾物资储备库应急能力评估提供了充分的理论依据⑤。寅峰等设计了效用替代率贪婪算法，并对算法进行了性能分析。通过数值算例，引入替代率从而提高物资储备的利用率，使物资储备在满足需求时利用率尽可能大⑥。林琪等基于蒙特卡洛仿真的求解算法，建立了考虑关联关系的应急物资储备决策模型，分析了模型最优解的特征，综合考虑应急物资与储备决策的关系和替代关系，确保在保证供应的前提下减少应急物资储备量⑦。

由于公共卫生事件暴发时具有传播范围广、传播速度快的特殊性，不同地区的传染面积不同，相对应的人口数量所需应急物资的数量必然存在差异，因此不同地区储备库储备的PPE数量也应不同。如何结合不同地区的实际情况，达到PPE的最优储备量，上述文献并未涉及这些问题。为此，笔者通过定义用于描述每个省、市、县级地区储备库所需的“PPE储备指标”，区分应在不同省市级储备点存储多少PPE，并根据紧急情况构建相应的储存量模型和PPE储备指标。

二、PPE储备指标数的提出

(一)PPE储备指标概念

根据Thomas L.Saaty的研究，用解决复杂组织和分析结构化的技术工具——AHP，通过量化决策标准权重的方法将问题分解层次结构，使其可以以独立方式进行分析和比较。构建此逻辑层次结构后，决策者可以通过对每个选定标准进行成对比较来系统地评估备选方案⑧。作为支持决策理论的主要数学模型之一，AHP的应用可以用来确定项目组合中的优先级的选择，为层次结构的每个元素得到一个可用于评估的数字权重和更直观的资源分配优先级别。考虑到防疫物资储备需要考虑的因素众多，笔者借鉴我国学者刘宗熹、赵启兰的理论，首次提出针对防汛物资的“应急物资储备指数”这一概念，通过描述每个物资储备点的应急物资储备的相对规模，减少了物资储备的随机性，有效解决了储备区中每个物资储备点的物资储备与当地灾害不匹配的问题⑨。

本文借鉴其他学者的研究思路及方法，结合突发公共卫生事件的传播特点和PPE物资的储备特性，有针对性地对X省的14个地州市的数据进行处理，为合理确定PPE的存储量,本文提出了“PPE储备指数”这一概念。本概念的提出通过AHP的应用，描述X省各市、县级PPE储备数量的相对大小的指标。该指数由各、市县级的经济、人口和医护从业人员数量三个因素决定。若得出指标数越大则意味着该市、县级的储备量相对于其他市、县级储备量越大。

(二)PPE储备指标数的作用

PPE储备指标数就是用来确定每个市（州）、县（市）的PPE战略储存点的应存量。PPE战略储存点应具有能在突发性的公共卫生事件暴发时，第一时间向该储存点覆盖的市（州）、县（市）及时输送足够量的PPE，以满足民众和医护人员基本防护需求。PPE储备指标数能够确保在不增加财政负担的前提下，弥补现有公共卫生应急物资的不足，形成一套重大突发公共卫生事件发生时可以统一调度的公共卫生应急物资保障体系。

三、模型的建构

根据突发性公共卫生事件的暴发特性，各地区的PPE需求量是由地区实际人口数量决定的,根据人均需求量就可以计算出总的需求量⑩。

(一)模型参数

Qi储备点的储备指数；δ为各地州市的PPE需求量；R公共卫生事件爆发下的为各地州市传播范围；T为各地州市的人口密度；d为PPE人均需求量；Di为各14个地州市的战略储备点的PPE最优储备量；φi为各战略储备点的传播系数。

(二)储备指标数模型的建构

根据突发公共卫生事件爆发的特点，PPE的战略储备指标由当地的经济、人口和医护从业员数量三个因素决定。将各储备站点的储备指标进行计算比较，若是得出的储备指数越大则表明该战略储存点的PPE应存量则越大，具体表示如下：

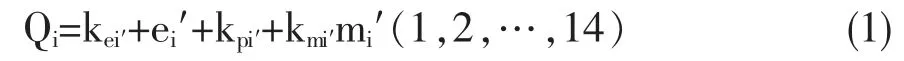
其中，ei′为第i个PPE的战略储存点的经济发展指数；pi′为第i个PPE的战略储存点的总人口指数；mi′为第i个PPE的战略储存点的医务从业人数指数。Kei′i、Kpi′i、Kmi′i表示三者的权重，由AHP计算方法得到Kei′i=0.202，Kpi′i=0.554，Kmi′i=0.244。对战略储存点的应存量影响最大的是人口，因此在经济、人口和医务从业人员三者的权重中，人口所占权重数最大。

针对公共卫生事件爆发时期不同地区遭受到的传染情况我们可知，即使在同一个省，不同市、县受感染的程度也不一样。一般来说，该市的经济发展的越好，公共卫生事件的传染速度也就越快，那么PPE战略储存点需要储备的物资也就越多，储备指数相应的也会越大。构建X省14个地州市的经济发展指标数时，选取了14个地州市2020年的GDP为评价标准，资料来源于《中国统计年鉴（2020）》⑩。计算模型为：

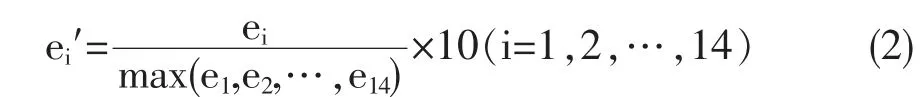
其中，ei为第i个战略储存点的GDP数值,ei′为第i个战略储存点的经济发展指标数。突发公共卫生事件爆发时，除经济发展指数外还有另一个重要的因素影响公共卫生事件传播速度的快慢，即当地的人口数。同一省的不同市，因人口总数不一样，人口密度也不一样，造成的传播速度也不一样。一般来说，人口越多，公共卫生事件传播速度越快，PPE战略储存点需要储备的物资也就越多。储备指数也会越大。构建X省14个地州市的人口指数时，选取了14个地州市2020年的总人口数为评价标准，资料来源于《湖南统计年鉴（2020）》⑫。计算模型为：

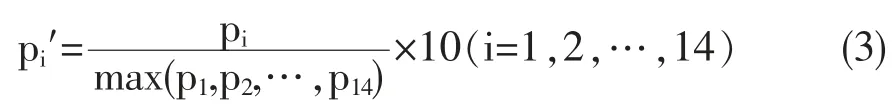
其中，pi为第i个战略储存点的人口总数，pi′为第i个战略储存点的人口发展指数。除了经济发展指数和人口指数会影响突发公共卫生事件在一个地方的传播速度以外，当地的医务从业者人数会直接影响PPE的消耗速度。一个地区医务从业人数越多，为全力遏制公共卫生事件的传播速度，所需要用的PPE数量也越多，PPE储备指数也越大。构建X省14个地州市的医务从业人员发展指数时，选取了各个地州市2020年的医务从业人员人数为评价标准，资料来源于《湖南统计年鉴（2020）》⑫。计算模型为：

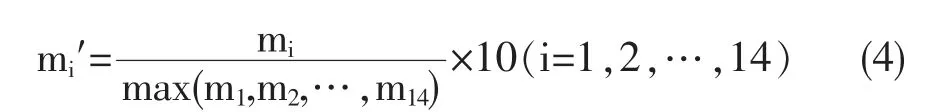
其中，mi为第i个战略储存点的医务人员总数，mi′为第i个战略储存点的医务从业人员发展指标数。

(四)最优储备量模型的建构

1.X省14个地州市PPE的需求量确定。每一个地州市的总PPE需求量由地区内公共卫生事件的传播范围、各地州市的人口密度和PPE的人均需求量决定。计算公式如下：

其中，模型参数δ为各地州市的PPE需求量；R为X省各地州市在以本次COVID-19为例的公共卫生事件中的传播范围；T为各地州市的人口密度；d为PPE人均需求量。

2.X省14个地州市的PPE最优储备量的确定。针对某一地级市的储存点用i表示，最优储备量模型公式为:

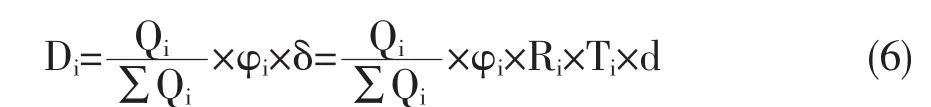
其中模型参数Di为各14个地州市的战略储备点的PPE最优储备量；Qi为各战略储备点的PPE储备指标数；φi为各战略储备点的传播系数。

传播系数φ的确定。本文是通过2020年国内学者赵序茅等在《基于大数据回溯新冠肺炎的扩散趋势及中国对疫情的控制研究》中利用大数据回溯COVID-19在我国扩散期间的总体趋势和传染系数⑬，通过建模计算得出实际的传播趋势和真实传播系数：φ1=0.57、φ2=2.33、φ3=0.42、φ4=0.79、φ5=1.51、φ6=0.37、φ7=0.77、φ8=0.98、φ9=0.07、φ10=0.38、φ11=0.73、φ12=0.04、φ13=0.34、φ14=0.46。真实的传播系数用来描述类似于COVID-19这类突发性公共卫生事件的综合强度、计算此类事件的传播趋势有重要作用。

四、实例分析

(一)PPE储备指标数的计算

本文以X省14个市州、县（市）为实例，通过上述的分析，PPE储备指数的计算公式如(6)所示，得出14个战略储存点的PPE储备指标数见表1。由表1可以看出，14个市州、县（市）的储备指标数表现出明显的差异。人口数越多的地级市，例如b、h和n市属于X省内人口总数位居前三的地级市，储备指标数明显大于其他地级市。

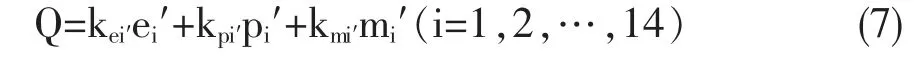
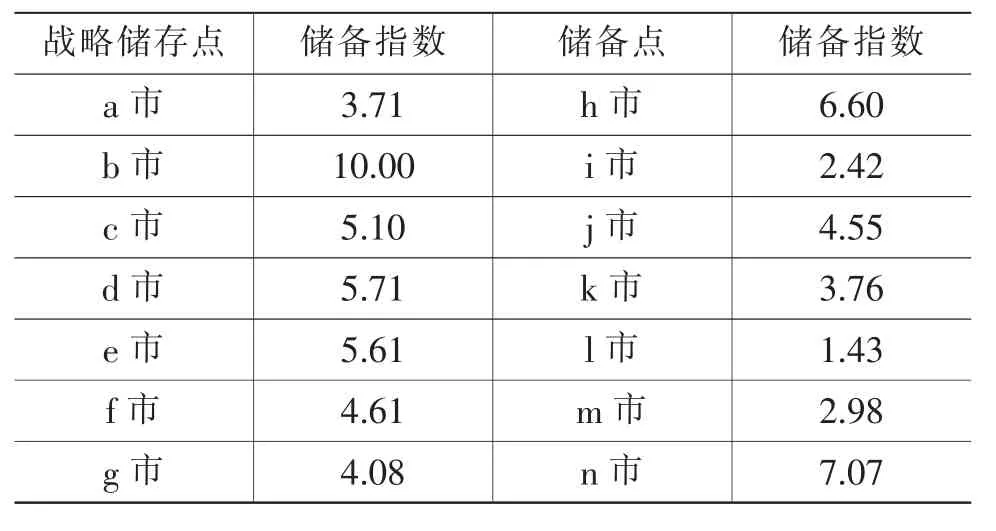
表1 战略储存点PPE储备指标数

(二)PPE储备指标数三维粒子图展示

依据储备指数的运算结果生成以下三个三维粒子图。影响储备指标数的三个变量经济发展指数(ei′)、人口指数(pi′)和医疗从业人员指数(mi′)，分别通过x轴和y轴和z轴体现。

从三维粒子图的展示中我们可以看出，X省14个地州市储备指数的整体趋势。如图(a)整体概览图所示，右边色条表示PPE的储备量。我们可以发现在X省的14个地州市中，b市为显眼的深灰色，在三维粒子图上的位置也远高于其他地级市，紧跟其后的是h市和e市。

将图(a)整体概览图拆分为两个独立的图表(b)和(c)可以更直观地发现，经济越发达的地区、医疗从业人员越多的地区、人口数越多的地区，储备量也就越大。例如，l市的人口和医疗从业人员人数为X省最少，经济发展水平也相对较慢，在三维粒子图上的位置也接近中心轴；而b市作为X省省会城市，经济发展水平、人口数和医疗从业人员人数都位居X省第一，储备量也最大。我们可以得出结论，ei′,pi′,mi′三个变量与Qi成正比。而三维粒子图对于揭示PPE的储备量与经济、人口和医疗从业人员这三个变量之间呈现怎样的分布趋势也有很直观的帮助。

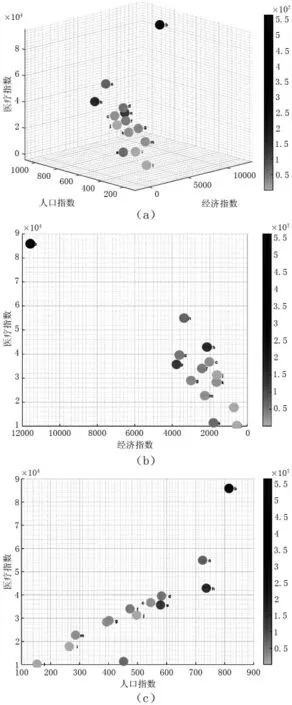
图1 X省各地级市PPE储备量三维粒子图

(三)PPE的最优储备数量计算

根据上述提到的PPE储备指标模型，计算14个市州、县（市）PPE的储备数量，将a-n市等依次编号为1-14,结合式(6),则:Q1=3.71、Q2=10、Q3=5.1、Q4=5.71、Q5=5.61、Q6=4.61、Q7=4.08、Q8=6.60、Q9=2.42、Q10=4.55、Q11=3.76、Q12=1.43、Q13=2.98、Q14=7.07。

以a市、b市、c市、d市、e市这五个地级市为例计算受灾范围R，取X省工信厅在COVID-19爆发时评估的全省122个县市区新冠肺炎疫情风险等级中高风险县市区的面积总和R，a市为7549km2、b市3947km2、c市3470km2、d市3599km2、e市4537km2；通过计算这5个地级市的面积和总人口数得出人口密度T，a市为0.037万人/km2、b市0.068万人/km2、c市0.028万人/km2、d市0.031万人/km2、e市0.038万人/km2。参照X省a市工业和信息化局公开的PPE采购清单中的指导意见，针对医用外科口罩这一PPE的人均需求量为128只/人。根据公式计算得出PPE类别中适用范围最大的医用外科口罩最优储备数量为（单位：只）：

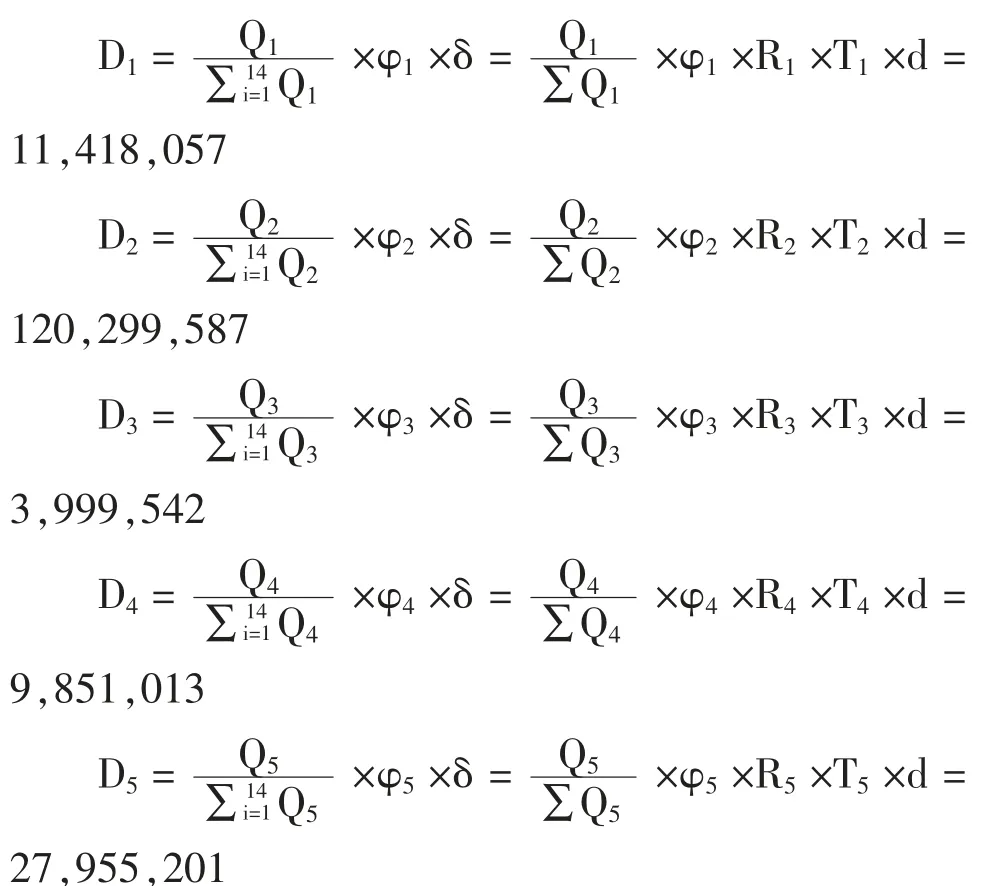
以此类推，计算出14个地州市的最优储备量如表2。

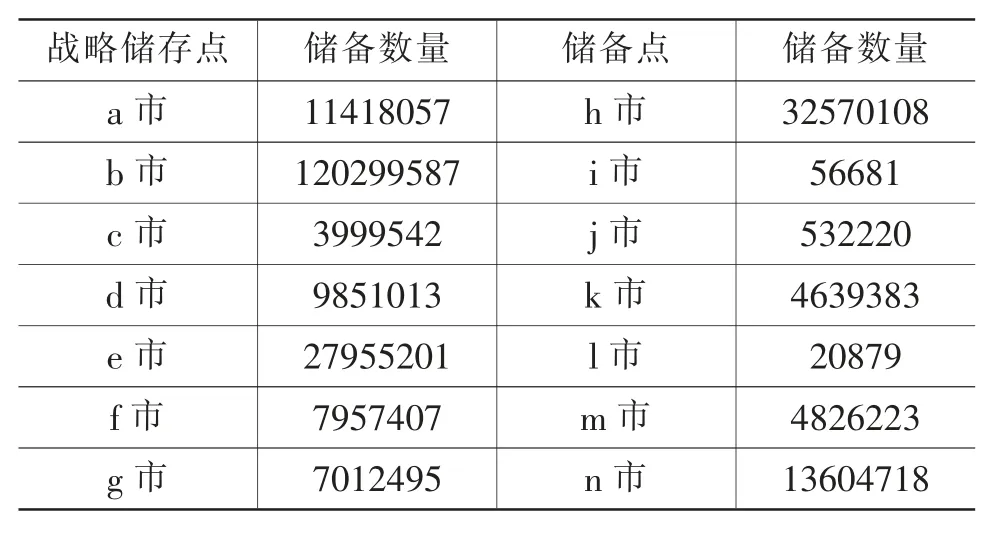
表2 医用外科口罩最优储备数量 （单位：只）

从表2中得出的计算结果我们可以看出，在全X省范围内，以医用外科口罩为例的PPE中，储备数量最多的防疫物资战略储备点为人口密度最大，经济发展水平最好的省会b市。另外一点值得我们注意的是，由于本文是基于COVID-19作为研究突发性的公共卫生事件的对象，Y省作为在本次COVID-19中感染情况最严重的地区，e市作为X省的所有地级市中最靠近Y省的地级市，受其影响，PPE储备数量也在X省的其他地级市中呈现出偏多的情况。

五、结束语

本文以X省PPE的最优储备量为研究对象，结合实证研究和AHP层次分析法，分解影响PPE使用需求的因素，构建PPE需求的计算模型，并引入了实例验证模型。

本文选择了X省的14个市州、县（市）作为研究对象，通过定义每个战略储存点所需的PPE储备的相对大小的PPE储备指标数，考虑不同地区的经济发展，人口数量和突发性公共卫生事件传播程度影响下的受灾人口所需的PPE数量等因素，建立了PPE的储备指标数模型。针对不同地区的受感染人口所需的PPE数量存在差异、战略储存点的储备等级不同的问题，计算出的结果对决策者求解各市州、县（市）的储备种类和数量有参考意义。与此同时，考虑到构建的战略储备点的储备指标模型可以作为PPE需求量计算依据，帮助PPE物资进行合理的储备和分配，从而可以降低成本，避免浪费。

注释：

①张海波.应急管理的全过程均衡:一个新议题[J].中国行政管理,2020(03):123-130.

②张红.我国应急物资储备制度的完善[J].中国行政管理,2009(03):44-47.

③Carias,C.,Rainisch,G.,Shankar,M.,Adhikari,B.B.,Swerdlow,D.L.,Bower,W.A.,Koonin,L.M.,2015.Potential Demand for Respirators and Surgical Masks During a Hypothetical Influenza Pandemic in the United States.Clinic

④董骏峰,肖娇,梁昌勇,王彬有.基于模块化的多层级储备库应急物资储备模型[J].中国安全科学学报,2018,28(11):182-188.

⑤蒲宇.救灾物资储备库应急能力评价研究[D].合肥工业大学,2019.

⑥徐寅峰,张敏娇,余海燕,鱼敏.基于效用替代率的物资储备量模型与算法[J].系统工程理论与实践,2011,31(02):270-275.

⑦林琪,赵秋红,倪冬梅.考虑关联与替代关系的应急物资储备量模型[J].管理科学学报,2018,21(08):112-126.

⑧Saaty,T.L.(2008).?Relative Measurement and its Generalization in Decision Making:Why Pairwise Comparisons are Central in Mathematics for the Measurement of Intangible Factors-The Analytic Hierarchy/Network Process.Madrid:Review of the Royal Spanish Academy of Sciences,Series A,Mathematics.

⑨刘宗熹,赵启兰.应急物资储备指数及储备量探讨[J].物流技术,2009,28(07):124-126.

⑩皮武良.基于博弈理论的国家医疗应急储备机制探究[J].财会通讯,2020(18):150-153.

⑪中华人民共和国统计局.中国统计年鉴[M].北京:中国统计出版社,2020.

⑫湖南省统计局.湖南统计年鉴[M].北京:中国统计出版社,2020

⑬赵序茅,李欣海,聂常虹.基于大数据回溯新冠肺炎的扩散趋势及中国对疫情的控制研究[J].中国科学院院刊,2020,35(3):248-255.