基于Fisher判别分析的塑料拖鞋XRF光谱鉴别

孙家政，姜 红，朱晓晗，务瑞杰，满 吉

(1.中国人民公安大学 侦查学院，北京 100038；2.北京华仪宏盛技术有限公司，北京 100123)

0 前言

随着人们生活水平的不断提升，人们对生活的品质和对日常用品舒适度的要求也在日益增加。拖鞋作为生活中的必需品，家庭中的每位成员普遍穿戴，尤其是在夏季，穿着拖鞋外出的人也屡见不鲜。在各类刑事案件现场中，侦查人员往往都能够在案发现场收集到拖鞋物证。通过对获取到的塑料拖鞋物证进行鉴别，能够为案件侦破提供有价值的线索，为刑事诉讼案件提供有力的证据[1-2]。

塑料拖鞋的成分主要有乙烯-醋酸乙烯酯共聚物(EVA)和聚氯乙烯(PVC)，由于EVA与PVC为可回收利用材料，故可作为原材料多次进行生产；然而，在二次生产的过程中会产生有害的物质[3]，如Pb、Cd等重金属元素。为适应市场的需求、提高产品质量，在塑料拖鞋的生产制作过程中会添加增塑剂和填料等，以增加产品的舒适度，延长使用寿命[4]。目前，检验塑料类材料的方法主要有红外分光光度分析法[5]、X射线荧光光谱法(XRF)[6]、拉曼光谱法[7]、差分拉曼光谱法[8]等。笔者采用XRF，使用典则(Fisher)判别分析法对X射线荧光光谱数据建立判别函数[9]，以期快速、准确且无损地对塑料拖鞋类物证进行检验。

1 实验部分

1.1 实验仪器及参数设置

X射线荧光光谱仪，X-MET8000Smart，电压为40 kV，电流为60 mA，Rh阳极靶，检测时间为60 s，北京华仪宏盛技术有限公司。

1.2 实验样品

不同来源的塑料拖鞋31个(样品表略)。

1.3 实验方法

用剪刀从鞋底部位裁剪1 cm×1 cm的小方片作为样品，将31个塑料拖鞋样品分别用酒精棉签进行擦拭、晾干后待测，将样品放于仪器探头下进行检测，并记录数据，数据在IBM SPSS Statistics统计分析软件中处理完成。

1.4 Fisher判别分析

Fisher判别分析是对数据降维处理的一种判别分析方法[10]。该方法是将样本点投影到一个固定方向，使得在该方向上样本的投影能尽量分开，表现为同类样本尽可能的紧凑，异类样本尽可能的分散(见图1)。由图1可以看出：两类样本点(圆形、三角形)在y=WTx方向上达到了显著的区分(W为样本投影向量)。

Fisher算法步骤为：

(1)

(2)

SW=S1+S2

(3)

Sb=(m1-m2)(m1-m2)T

(4)

(5)

式中：mi为各类样本的均值向量；Ni为类Wi的样本个数；X为样本点向量；Si为样本类内离散矩阵；SW为总类内离散矩阵;Sb为样本类间离散矩阵。

2 结果与讨论

2.1 X射线荧光光谱的分析结果

对31个样品进行XRF检测，检测结果见表1。PVC材质中含有Cl元素，而EVA材质中不含Cl元素。根据X射线荧光光谱仪在样品中是否检出Cl元素，将样品分为2类。然后按照样品中是否加入了助剂硫酸钡(BaSO4)，即是否检测出Ba元素，可进一步将样品分成4组。Pb盐作为塑料稳定剂，不仅价格低廉，而且可以提高塑料拖鞋的稳定性能。Cd染料作为一种十分稳定的无机染料，其同时具备良好的耐热性，在塑料拖鞋的染色中广泛使用[12]。故Pb元素和Cd元素在塑料拖鞋生产过程中必不可少，按照Pb、Cd元素的存在情况，最终将31个样品分成了10组(见表2)。

表1 样品XRF结果

对同一组中的样品，可以根据Ca与Fe元素含量的比值(w(Ca)/w(Fe))进一步区分。例如：同时含有Cl、Ba、Cd、Pb元素的样品(表2中的第1组)，其w(Ca)/w(Fe)分别为：3.09、600.38、54.57、107.64、29.65、19.45、26.42。即使是同一厂家出产的拖鞋，不同系列样品中的元素含量也存在一定的差异，也可根据其w(Ca)/w(Fe)的不同进行区分。

表2 31个样品分类结果

2.2 Fisher判别分析结果

表3为Fisher判别函数摘要表。由表3可以看出：前2个判别函数的特征值为24.182和12.696，累计比率为92.1%，反映出第一、第二判别函数的均方差的表示效果好，并且其正则相关系数也相对较大，即可建立二维的直角坐标系[12]。对判别函数的判别能力进行分析评价，当显著性值低于0.05时，该判别函数显著性水平高，相应的判别能力也较强[13]。对于第一、第二判别函数，显著性值分别为0与0.001，均明显小于0.05；其余判别函数对应的显著性值大于0.05，不具有统计学意义[14-16]，最终选取前两个判别函数进行Fisher判别函数的构建。

表3 判别函数摘要

表4为Fisher判别函数系数表。

表4 Fisher判别函数系数

由表4可列出第一、第二判别函数y1、y2分别为：

y1=0.369x1+0.583x2-0.001x4+0.001x5+

0.152x6+0.001x7-15.155

(6)

y2=0.519x1+0.515x2-4.39x3-0.001x4+

0.025x6+0.001x7-15.253

(7)

式中：x1为Cl；x2为Ca；x3为Ti；x4为Fe；x5为Zn；x6为Cd；x7为Ba。

建立直角坐标系(见图2)，根据元素的原始变量(x1～x8)可确定样本的坐标分布图。计算出样本的组质心在(-15.155，-15.253，-7.333，-95.464，-86.985，-10.890，-38.455，-32.054，-26.100，-17.579)区域上，这10组样本的组质心在分布图的位置见表5。从图2可以看出样本的组质心在Fisher判别函数联合分布图中的散布情况，31个样本相聚于10个类别的组质心密集分布[17]，效果较为理想。

表5 组质心分布

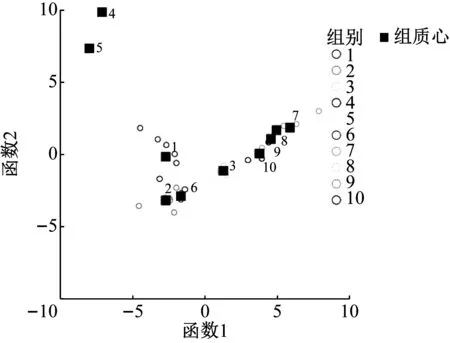
图2 判别函数联合分布图

3 结语

利用XRF，快速高效地对塑料拖鞋样本进行了检验，该方法无损检材且结果准确可靠。根据检测出样本中无机元素含量的不同，可将31个塑料拖鞋样本分成10组，对同组中的样品根据w(Ca)/w(Fe)的不同加以区别。通过建立Fisher判别分析，选取了判别效果相对较强的第一、第二判别函数，最后建立了Fisher判别函数分布图，分类效果较好，该方法可为犯罪现场塑料拖鞋物证的检验鉴别提供一定的参考价值。