铁路新活载双孔重载加载方法探讨
2022-04-24王雨权
王雨权
(中国铁路设计集团有限公司,天津 300308)
铁路列车活载是铁路列车对结构工程静态作用的概化表达形式,对于铁路桥涵结构的设计影响巨大[1-5]。随着铁路事业的快速发展,我国制定了多种活载类型,如ZK、ZC、ZH、ZKH,分别使用于高速铁路、城际铁路、客货共线铁路、重载铁路等[6-10],同时,随着海外铁路项目的推进,还需要研究制定适合海外需求的各种活载[11-13]。
目前ZK、ZC、ZH、ZKH等活载的标准图式,可以归类为图1的形式,不同的距离和载荷数据代表不同活载。
如图1中S1=S5=0.8 m,S2=S3=S4=1.6 m。集中荷载大小F1=F2=F3=F4=200 kN,线荷载大小F01=F02=64 kN/m,则该图即可表示为ZK标准活载图式。如F1=F2=F3=F4=150 kN,F01=F02=48 kN/m,则该图示即可表示ZC标准活载图式。如取其他值,则表示其他活载类型。
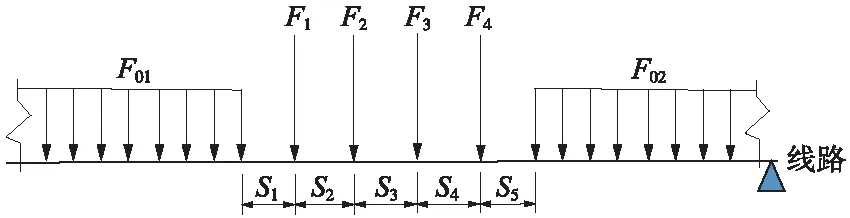
图1 新活载通用图示
列车活载的大小直接影响梁、墩台及桩基的设计。为此,我国在大规模铁路桥梁建设过程中,进行了活载对桥梁建设影响的各种研究[14-18]。
对于一个特定的列车活载,在墩台和基础设计中,前辈们根据检算内容的不同,提炼出几种控制性工况,如单孔轻载、单孔重载、双孔轻载、双孔重载等控制性工况[19-20]。
单孔轻载、单孔重载物理意义比较简单,求解时只需根据单孔梁的影响线,把集中荷载部分放在影响线的最大、最小处即可求得。但对于双孔重载和双孔轻载则稍微复杂,因双孔重载和双孔轻载对于一个简支梁组合来说,是一个共轭关系,因此这两个工况的求解过程的本质是一样的。
下文推导公式即按照图1中的符号表示。单孔重载和单孔轻载的表达式比较简单,限于篇幅,仅重点介绍双孔重载计算。
1 现有方法合理性探讨
1.1 现有方法合理性初探
现有设计手册均以“中-活载”为研究对象。以图2为例,双孔重载的布置应该使得R2+R3最大,这就需要解决一个加载点计算问题。
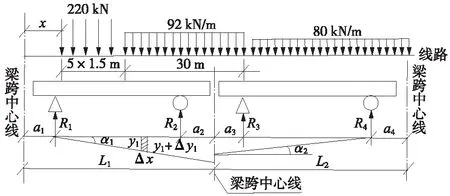
图2 “中-活载”加载示意
由铁一院主编的设计手册《桥梁墩台》[21]在求解双孔重载加载点时给出了一个计算原则,即当G1/(L1-a1-a2)=G2/(L2-a3-a4)时,R2+R3最大。经了解,某设计院原有相关计算程序在计算“中-活载”的双孔加载时,也是采用这一原则来寻找最佳加载位置。
式中,G1、G2为左右两侧梁跨上承担的荷载值;L1、L2为左右梁跨的梁跨总长;a1、a2、a3、a4为各支座到梁跨中心线的距离。
经过研究发现,利用该原则计算出来的并不是R2+R3的最大值位置。下面用一个在研究“中-活载”时找到的反例进行验证。
图2中,假设梁长L1=L2=12.28 m,因为L1=L2,上述判据可以简化为G1=G2。
设“中-活载”的第1个集中力距左侧梁边缘距离为x,此时左侧梁跨的总荷载可表示为G1=1 100+(12.28-x-7.5)×92,对应右侧梁跨总荷载为:G2=1 129.76kN。由G1=G2可得:x=4.46 m。
在求得加载点x=4.46 m后,根据弯矩平衡即可求得此时桥墩所受总压力R2+R3=1 235.88 kN,该值即为现有方法的计算结果。
但如果将图2中第5个集中荷载作用于两孔梁的交点位置,x值为6.28 m。此时桥墩所受总压力R2+R3=1 393.13 kN。
由此可见,将第5个集中荷载作用于两孔梁的交点位置时,所得到的总支反力大于按照现有方法G1/(L1-a1-a2)=G2/(L2-a3-a4)判据得到的总压力。
因此,判据得到的活载布置位置只是其中一个临界点,但并不是极值点。
1.2 理论论证
下面通过理论推导来论证现有方法求得的起算点x值并不一定是极值点。
根据定义可知,当列车“中-活载”移动到极值点位置时,桥墩所受的压力之和最大,也即R2+R3值最大。因而荷载由极值点位置不论向左或向右移动到临近位置时,R2+R3值均应减小,这一过程可用数学极值表示
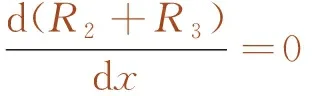
(1)
如图2所示,设左、右两侧梁跨的影响线倾角分别为α1、α2,当整个“中-活载”向左或向右移动一微小距离Δx时,相应的R2+R3值为
R2+R3=P1(y1+Δy1)+P2(y2+Δy2)+…+
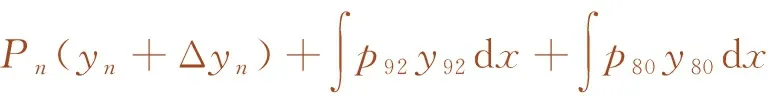
(2)
式中,R2、R3为计算桥墩上作用的两侧梁的支反力;P1、P2,…,Pn为影响线上“中-活载”的集中荷载;y1、y2,…,yn为P1、P2,…,Pn荷载对应的高度;Δy1、Δy2,…,Δyn为因向右移动一微小距离Δx时影响线上P1、P2,…,Pn荷载对应的高度变化量;p92、p80为均布荷载;y92、y80为均布荷载对应影响线高度。
下面可以论证原计算原则只是式(1)的一个特例,即当两孔梁上只作用集中荷载,且梁长及支座到梁跨中心线的距离均对称相等时,式(1)代表的通用判据与G1/(L1-a1-a2)=G2/(L2-a3-a4)是等价的。
当梁上只作用集中荷载时,荷载向左或向右移动一微小距离Δx时,可得对应的支反力的增量为
Δ(R2+R3)=P1Δy1+P2Δy2+…+PnΔyn=
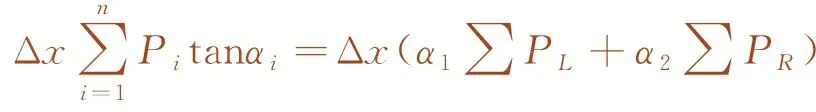
(3)
式中,α1、α2为图2中左右两侧影响线的倾角,符号相反,因α1、α2为小角度,近似有αi=tanαi(i=1,2),PL、PR分别为作用于左右两侧梁上的荷载值。当梁长及支座到梁跨中心线的距离均对称相等时,α1与α2大小相等,方向相反。
由式(1)、式(3)及Δx不为零可知,在极值条件下,Δ(R2+R3)为零,可进一步得到α1∑PL+α2∑PR为零。而由于α1=-α2,可得∑PL=∑PR。
而对于判据G1/(L1-a1-a2)=G2/(L2-a3-a4),当梁长及支座到梁跨中心线的距离均对称相等时可得G1=G2。此时与∑PL=∑PR结论一致。
但对于“中-活载”来说,存在均布荷载。也即式(2)中的积分项不能略去。且对于任意梁跨组合,其左右两侧的梁长也并不一定相等,支座到梁跨中心线的距离也不一定对称,在此情况下,是无法得到与判据G1/(L1-a1-a2)=G2/(L2-a3-a4)一样的结论的。
因此,传统寻找加载点的计算方法所求得的位置,并不一定能满足极值点要求,据此计算得到的起算点的科学性有待商榷。
2 利用极值求导法求算双孔重载
双孔重载,可用于检算桥墩的墩身强度、基底最大应力和稳定性,对于ZK、ZC、ZH、ZKH等新活载图式,目前还缺乏相关的资料用于求解支反力。
由于双孔重载应该使得桥墩两侧两孔梁的支反力之和R2+R3最大,从数学角度来讲,此时应该就是R2+R3对加载位置x的导数为0的驻值点位置,因此,求解加载点位置可采用极限求导的方法进行。
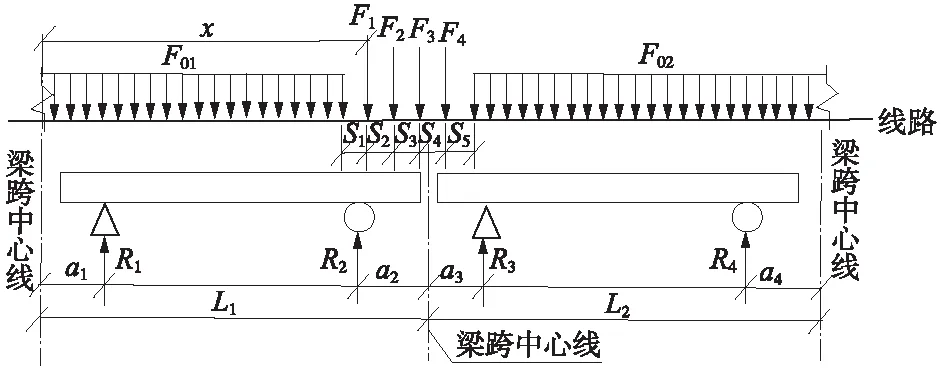
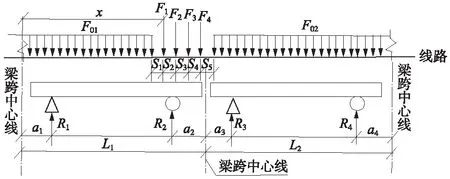
为使推导的计算公式尽量适应更多类型的活载,以图1所示的活载通用形式为推导依据。双孔重载的计算图式见图3。
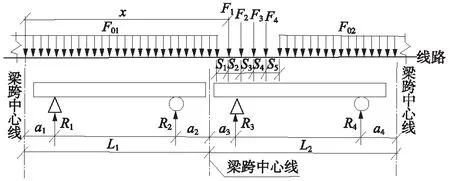
图3 新活载之双孔重载图式
图3中,假设6 m≤L1≤L2,x为左侧梁端到第一个集中荷载的距离,由于左右两侧梁长L1、L2可以有不同的组合,加载计算点也可布置在不同的位置,这两个因素都会影响R2+R3的具体表达式。因此,可根据左侧梁跨上出现的集中力个数来区分计算工况及其对应的边界条件。由于集中荷载有4个,因此可出现5种工况。对这5种工况,分别建立R2和R3的表达式,然后对R2+R3求导数,并令其导数为零,求出加载点x值。然后判断计算得到的x值是否满足与梁长的关系,如满足,则将得到的x值分别代入R2和R3的表达式,即可求得每种工况的双孔重载值,下面对这5种工况分别进行公式推导。
2.1 左侧梁中有1个集中荷载F1
如图4所示,左侧梁中布置1个集中荷载F1,根据图示,写出R2和R3的力矩平衡方程如下
(4)
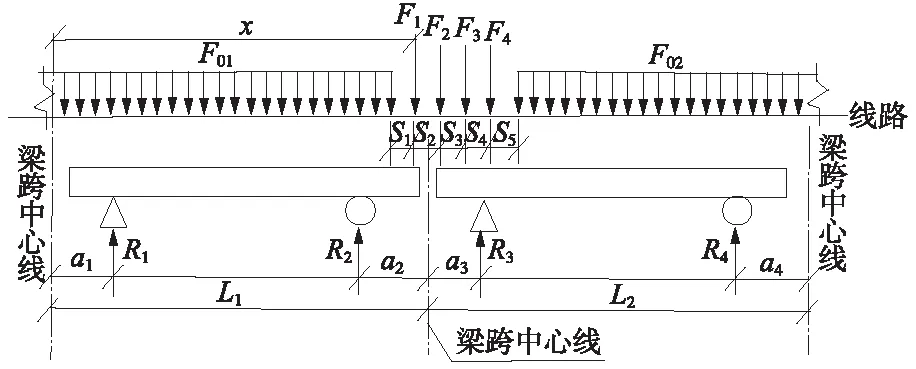
图4 工况1活载加载示意
经整理,可分别写出支反力R2和R3的表达式
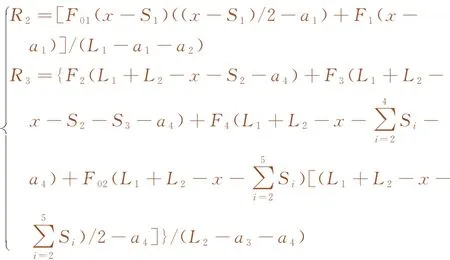
(5)
由R2+R3值对x求导,即
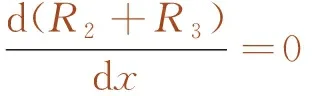
(6)
可得加载位置的表达式为
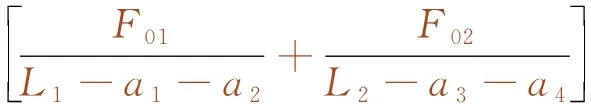
(7)
通过式(7)计算得出x值后,尚需检算该工况的梁长与x值的关系式是否满足下列条件
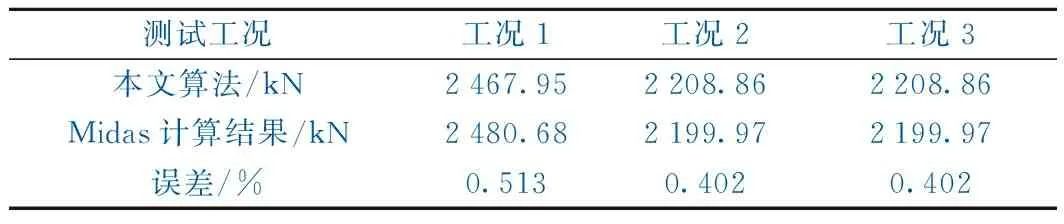
L1-S2 (8) 如满足式(8)的判别条件,可将x值代入式(5)的表达式,求出R2和R3的值,此时的R2+R3即为本工况的双孔重载值。 特别指出的是,式(8)是保证左侧梁中分布一个集中力F1的必要条件。 如图5所示,左侧梁中布置2个集中荷载F1、F2,根据图示,写出R2和R3的力矩平衡方程如下 (9) 图5 工况2活载加载示意 经整理,可分别写出支反力R2和R3的表达式 (10) 由R2+R3值对x求导,可得加载位置为 (11) 通过式(11)计算得出x值后,尚需检算该工况的梁长与x值的关系式是否满足条件 L1-S2-S3 (12) 如满足式(12)的判别条件,可将x值代入式(10)的表达式,求出R2和R3的值,此时的R2+R3即为本工况的双孔重载值。 如图6所示,左侧梁中布置3个集中荷载F1、F2、F3,根据图示,同样可写出R2和R3的力矩平衡方程式,然后求出各自表达式如下 (13) 图6 工况3活载加载示意 由R2+R3值对x求导,可得加载位置为 (14) 通过式(14)计算得出x值后,尚需检算该工况的梁长与x值的关系式是否满足条件 L1-S2-S3-S4 (15) 如满足式(15)的判别条件,可将x值代入式(13)的表达式,求出R2和R3的值,此时的R2+R3即为本工况的双孔重载值。 如图7所示,左侧梁中布置4个集中荷载F1、F2、F3、F4,根据图示,同样可写出R2和R3的力矩平衡方程式,然后求出各自表达式如下 (16) 图7 工况4活载加载示意 由R2+R3值对x求导,可得加载位置为 (17) 通过式(17)计算得出x值后,需检算本工况梁长与x值的关系式是否满足条件 0≤x≤L1-S2-S3-S4 (18) 如满足式(18)的判别条件,可将x值代入式(16),求出R2和R3的值,此时的R2+R3即为本工况的双孔重载值。 对于左侧梁中没有分配集中荷载的情况可参见图3。根据图示写出R2和R3的力矩平衡方程式,然后求出各自表达式如下 (19) 由R2+R3值对x求导,可得加载位置。先对R3求导得 (20) 对于R2,可分为两种情况。 当L1≥x-S1时 (21) 此时 (22) (23) 通过上式计算得出x值后,进一步验算本工况的梁长与x值的关系式是否满足条件 L1 (24) 如满足式(24)的判别条件,可将x值代入式(19)的表达式,求出R2和R3的值,此时的R2+R3即为本工况的双孔重载值。 当L1 (25) (26) 通过式(26)计算得出x值后,需验算本工况的梁长与x值的关系式是否满足条件 L1+S1 如满足式(27)的判别条件,可将x值代入式(19)的表达式,求出R2和R3的值,此时的R2+R3即为本工况的双孔重载值。 将上述计算公式编制成表格,然后针对高铁桥梁设计中常用的简支梁梁跨组合进行计算测试,计算结果与Midas结果进行对比验证。 公式验算的表格形式如表1所示,Midas计算采用“所有点”法加载,并利用Midas的并发反力功能,查找出当R2+R3值最大时的加载位置及此时双孔重载值。 表1 新活载计算公式验证计算 表1中的a1、a2、a3、a4及L1、L2、x的含义与图2一致。 下面以ZK活载为例,分别测试如下梁跨组合,并将测试结果汇总于表2。 工况1的梁跨组合为:L1=32.7 m,L2=32.7 m,a1=0 m,a2=a3=a4=0.35 m。 工况2的梁跨组合为:L1=32.7 m,L2=24.7 m,a1=a2=a3=a4=0.35 m。 工况3的梁跨组合为:L1=24.7 m,L2=32.7 m,a1=a2=a3=a4=0.35 m。 表2 与Midas计算结果对比 从上面3组测试工况的对比结果来看,本文所推导的算法与商业软件Midas的计算结果对比,最大误差为0.513%,不超过1%,计算精度满足工程设计要求。 上述误差产生的原因,经分析可能存在两种情况:其一,Midas加载计算中,采用的空间梁单元是一个弹性体,而本文所推导的公式忽略弹性变形,公式建立在刚体范畴内;其二,Midas加载计算中,移动荷载分析所采用的“所有点”法,是一种数值解,计算过程中,程序内部划分移动步距,导致在计算时得到的极值点并不是精准的极值点。 本文对简支梁活载加载计算中现有的双孔重载极值点求解方法进行了评述,从算例及理论两方面对原有计算方法的科学性进行了论述。并基于新型活载的参数化表示方法,提出了极值求导法求解双孔重载加载点位置,分5种工况给出了各梁跨组合的双孔重载表达式。主要结论如下。 (1)桥墩设计中,现有的双孔重载加载点计算方法存在缺陷,该方法只有在两侧梁跨相等且无均布荷载情况下成立。 (2)双孔重载加载点计算中,原有计算方法是本文所述极值求导法的一个特例。 (3) ZK、ZC、ZH、ZKH等新型活载,可采用统一的参数化标准图式,荷载图式中,只需要各参数取值不同,即可代表不同类型活载。 (4) 根据梁跨组合情况给出的5种计算工况,能包络所有加载情况,不同工况也体现在需满足的边界条件有所不同。 (5) 以高铁桥梁设计中常用的简支梁梁跨组合进行计算测试,结果表明,与Midas的计算结果误差不超过0.513%,计算精度满足工程设计要求。2.2 左侧梁中有2个集中荷载F1、F2
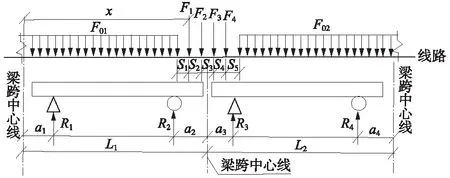
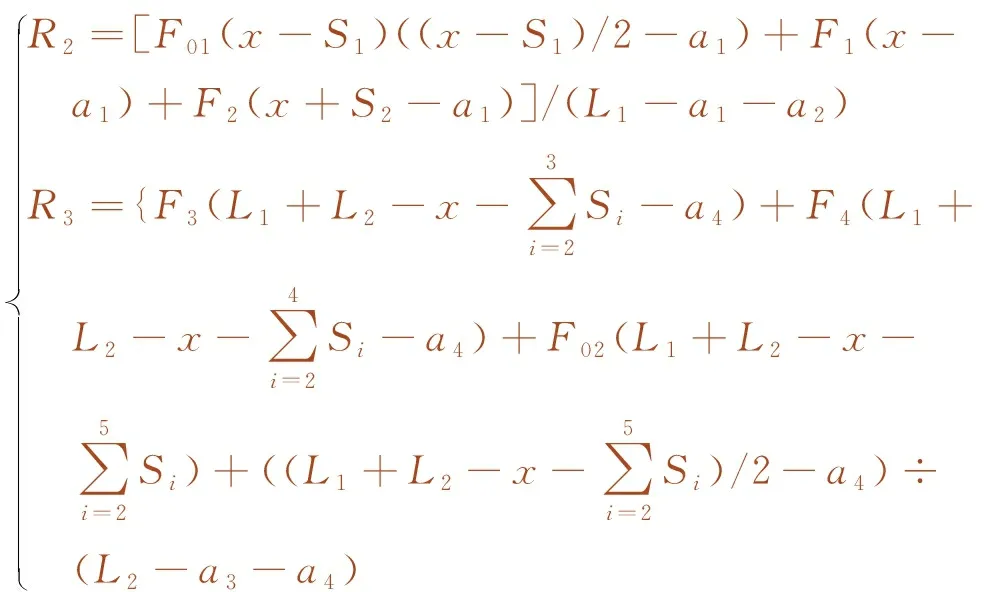
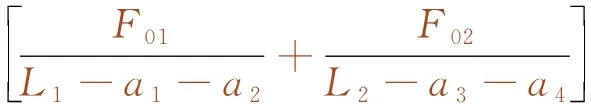
2.3 左侧梁中有3个集中荷载F1、F2、F3
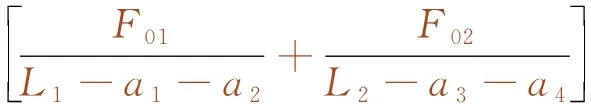
2.4 左侧梁中有4个集中荷载F1、F2、F3、F4
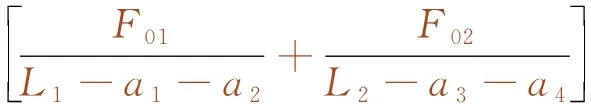
2.5 左侧梁中无集中荷载
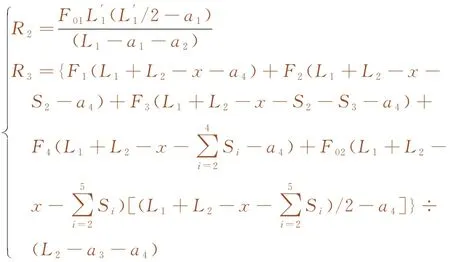
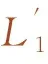
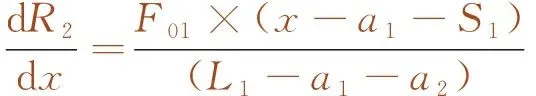
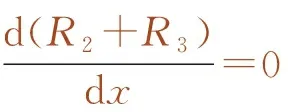
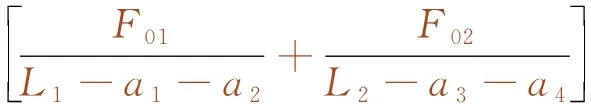
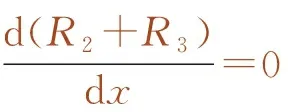
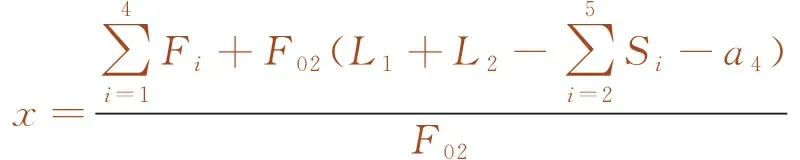
3 数值验证

4 结论
