基于JFNK的两流体三流场两相流模型的全隐算法研究

樊 杰 吴和鑫 苟军利 单建强

（西安交通大学核科学与技术学院 西安 710049）

对于环状流下干涸以及干涸后的传热以及核反应堆再淹没传热，液滴的传热传质在其中扮演了重要的角色，目前主流的核反应堆系统分析程序大都采用两流体两相流模型，没有模拟液滴效应，传热计算有一定的误差，而三流场两相流模型考虑了液滴的流动传热，成为核反应堆安全分析程序发展的方向。

目前国际上基于两流体三流场的两相流模型或者 核 反 应 堆 安 全 分 析 程 序 有CATHARE3［1］、SPACE［2］、CUPID［3］、TRAC-M［4］、C3DM［5］以 及Frepoli等［6］和笔者所在的核安全与运行实验室所开发的三流场两相流模型［7］，除Frepoli开发的基于漂移流的两流体三流场模型外，其余这些模型或程序都采用半隐数值算法，与其他基于半隐数值算法的核反应堆安全分析程序一样，例如：RELAP5，数值稳定性受声速库仑特值的影响。而全隐数值算法是绝对稳定的，因此也成为核反应堆系统分析研究的一个热点。

目前大部分的基于全隐数值算法的程序都基于传统的牛顿迭代法，例如：Frepoli开发的两流体三流场模型、CATHARE2［8］等，而传统的牛顿迭代法需要形成雅克比矩阵，对于本构模型较多的两流体模型雅克比矩阵的形成具有一定的困难，因此近年来一种无需雅克比矩阵的牛顿-Krylov迭代法（Jacobianfree Newton-Krylo，JFNK）被用于两相流模型的全隐数值算法，当前JFNK用于两相流模型全隐数值算法的研究还不够成熟，且集中于漂移流模型或者两流体模型，如：Ashrafizadeh等［9］、Hajizadeh等［10］、Hu等［11］、Wu等［12］的漂移流模型，Mousseau等［13］、Zou等［14］的两流体模型，在公开文献中基于JFNK算法的两流体三流场模型的全隐算法的相关研究还没有，因此本研究尝试对先进的两流体三流场两相流模型开发基于JFNK算法的全隐数值算法。

本研究针对两流体三流场两相流模型，建立基于JFNK算法的全隐算法，并针对三流场中某一相或两相缺失造成的数值计算困难进行了特殊的数值处理。程序模拟了Ransom水龙头数值标准题，以验证数值算法的精度，并通过模拟过冷沸腾实验和Dryout传热实验以验证程序计算单相、单相到两相的过渡、没有液滴的两相和三流场两相等工况下数值算法的精度。

1 数学模型

两相流数学模型采用一维两流体三流场模型，分别对气相、连续液相和弥散液滴相建立质量、动量和能量方程，模拟了气液之间的传热传质以及连续液相与弥散液滴相之间的夹带沉降，气相的质量守恒方程为：

式中：右边项分别为单位体积的相间传质量和壁面传质量。

液相的质量守恒方程为：

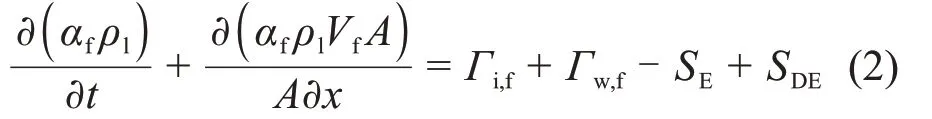
式中：右边项分别为连续液相与气相的相间换热量、壁面传质量、液滴夹带量、液滴沉降量。

液滴相的质量守恒方程为：

气相的动量守恒方程为：

式中：右边项分别为弥散液滴与气相的相间换热量、壁面传质量、液滴夹带量、液滴沉降量。

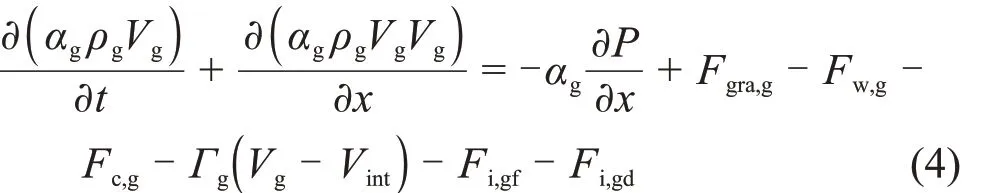
式中：右边项分别为压力梯度项、重力项、壁面摩擦力、局部阻力、相间传质引起的动量转移、气相与连续液相的相间摩擦、气相与弥散液滴的相间摩擦。

液相的动量守恒方程为：

式中：右边项分别为压力梯度项、重力项、壁面摩擦力、局部阻力、气相与连续液相的相间摩擦、相间传质引起的动量转移、液滴夹带沉降引起的连续液相的动量转移。

液滴相的动量守恒方程为：

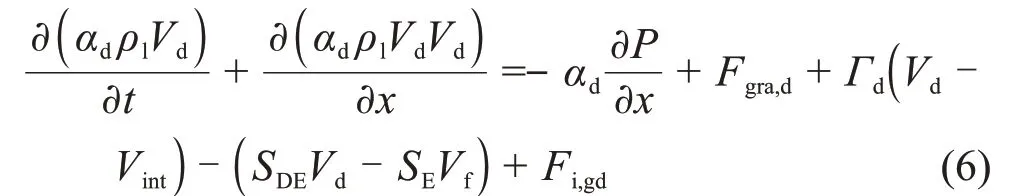
式中：右边项分别为压力梯度项、重力项、相间传质引起的动量转移、液滴夹带沉降引起的弥散液滴的动量转移、气相与弥散液滴的相间摩擦。

气相的能量守恒方程为：

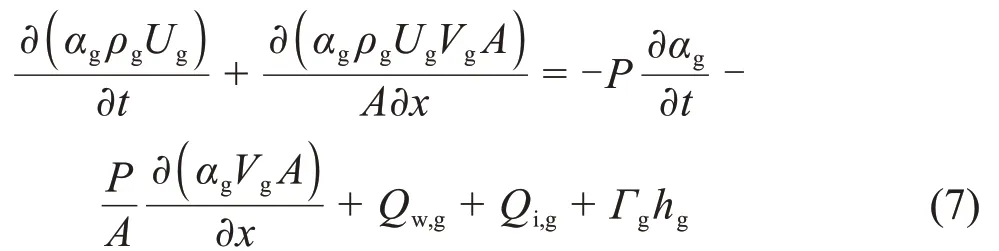
连续液相和弥散液滴相被认为是热平衡的，液相和液滴相合成一个液相的能量方程，即：

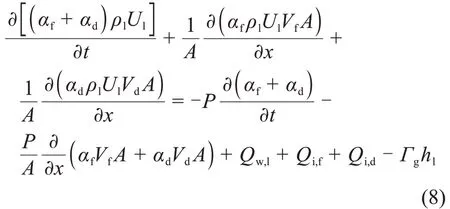
式中：右边项分别为压力做功项、壁面换热量、相间换热量、传质引起的能量转移项。

两流体模型守恒方程封闭需要的本构模型包括相间换热、相间摩擦、壁面换热、壁面摩擦、液滴夹带沉降等模型，这些本构模型与流型和换热模式有关，程序中根据计算工况的需要选用相应流型或换热模式下的模型，各模型的具体形式详见文献［7］。

2 数值算法

2.1 全隐数值离散

守恒方程离散采用基于交错网格的有限体积法，时间差分采用向后的欧拉法，空间离散采用Van Albada［15］高阶精度差分格式，求解变量依次为气相内能、液相内能、空泡份额、液相份额、压力、气相速度、液相速度和液滴速度。

对于控制体i，其守恒方程有汽相能量方程FUg，i、液相能量方程FUl，i、汽相质量方程Fαg，i、连续液相质量方程Fαf，i、弥散液滴质量方程FPi，对于接管i+1/2，其守恒方程有汽相动量方程FVg，i+12、液相动量方程FVf，i+12、液滴相动量方程FVd，i+12。此处展示了弥散液滴相质量守恒方程、汽相动量守恒方程、液相能量守恒方程等3个方程的全隐式离散形式。

弥散液滴相质量守恒方程：

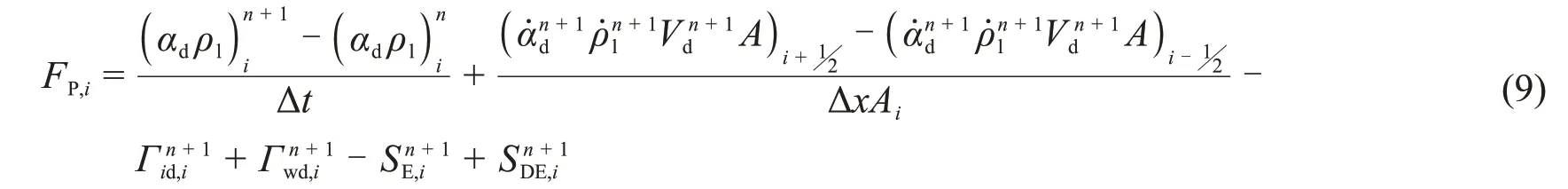
汽相动量守恒方程：

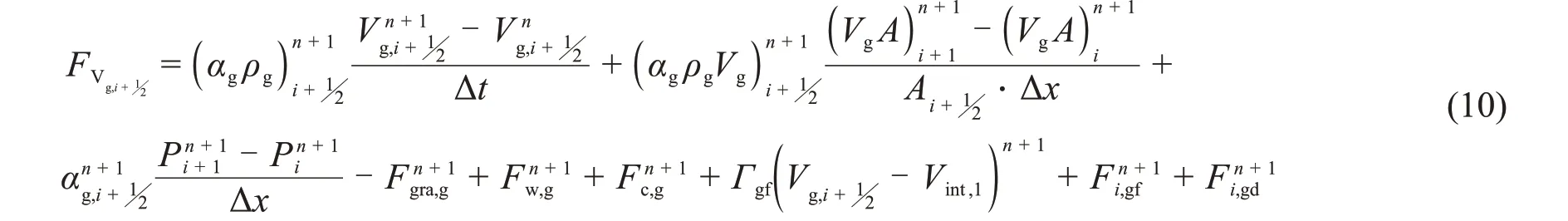
液相能量守恒方程：

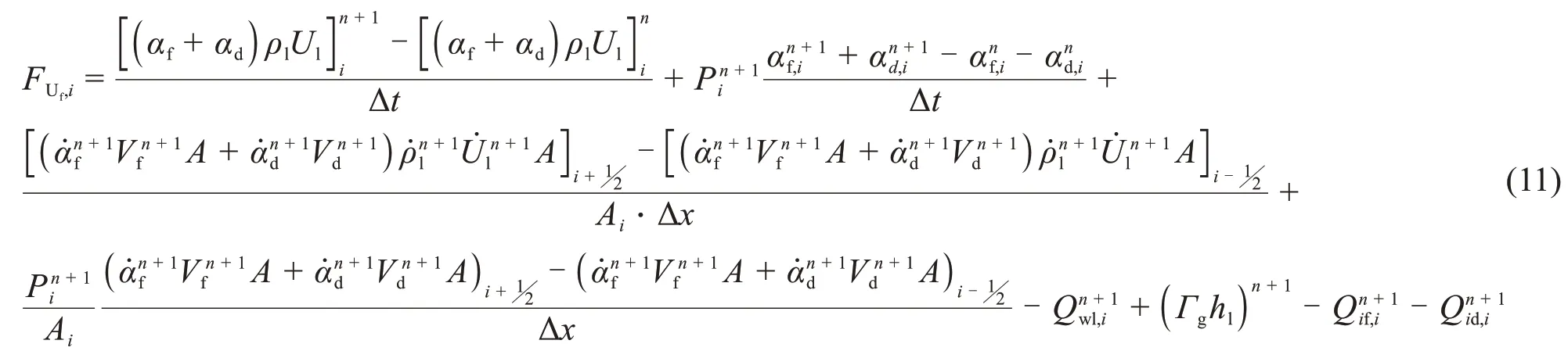
2.2 JFNK算法

对于由所有控制体质量和能量离散方程以及所有接管动量离散方程形成的方程组，由JFNK算法求解，外迭代是经典牛顿法，牛顿迭代的基本格式为：

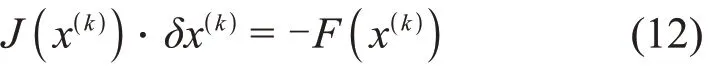
对于该线性方程组，使用Krylov子空间迭代法进行求解，常用的Krylov子空间迭代法为GMRES算法。迭代过程中无需写出雅克比矩阵，只需要雅克比矩阵与向量的点积，可以使用差分近似代替微分，即：

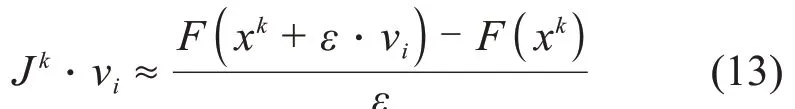
式中：ε为差分步长或者扰动参数［16］：

式中：N为线性方程组中方程的个数；a为机器精度。

对于JFNK算法，合适的预处理技术可以有效地加快Krylov子空间迭代的收敛。JFNK方法中常用的线性预处理方式有：左预处理、中间预处理、右预处理等，由于右预处理技术不会改变方程的右边残差项，有利于JFNK方法中Krylov子空间迭代收敛准则的选取，因此本研究中采用右预处理，即：

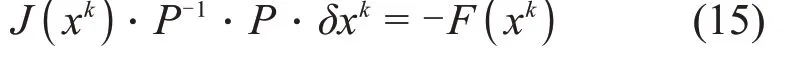
预处理矩阵P与雅克比矩阵J越接近，Krylov子空间迭代收敛越快，由于半隐式离散得到的雅克比矩阵与全隐式离散得到的雅克比矩阵在形式和量级方面都是相似的，因此半隐式离散的雅克比矩阵被当作预处理矩阵。

2.3 单相问题数值处理

当使用两流体三流场模型计算两相流时，可能会遇到某一相或者两相不存在，例如：单相水、液滴不存在的泡状流和弹状流、连续液相不存在的弥散流、单相汽等，缺失相的守恒方程是不存在的，此时线性方程组和预处理矩阵都是奇异的，之前基于半隐算法三流场模型的研究中，给缺失相一个很小的份额用于计算相间换热和相间摩擦，使得相间换热和相间摩擦不为零，可以解决线性方程组奇异的问题。例如：对于泡状流，由于没有液滴，因此液滴的动量守恒方程简化为：

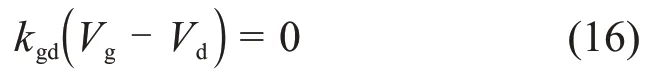
由于使用很小的液滴份额计算相界面面积，因此相间摩擦系数不为零，这样得到的液滴速度等于汽相速度。然而，缺失相的份额在守恒方程中仍然是0，当进行“Jacobian-Free”步骤时，新的(x k+ε·x k)中液滴份额仍然是0，在差分步中液滴份额没有贡献，因此会产生非物理的解。

因此在当前研究中，汽相和连续液滴相的份额为10-5~0.999 99，液滴份额为10-4~0.999 9，经过这样的数值处理，相间摩擦和相间换热是连续的，在各种流型之间转换时不存在数值困难。且在“Jacobian-Free”步骤中，(xk+ε·x k)中各相的份额均不等于x k中的相份额，因此不会产生非物理的解。虽然缺失相的源项不等于0，但相份额很小，数值误差时是可以接受的。

2.4 程序计算流程

程序的计算流程如图1所示，主要包括JFNK算法模块和本构模型计算模块。JFNK算法模块包括矩阵预处理、GMRES迭代和牛顿迭代，使用JFNK完成线性方程组的求解后进入下一时间步的计算直至瞬态计算结束。在JFNK算法模块中，x以及离散方程组的残差F（x）在不断地更新，需要通过本构模型计算模块不断地赋值计算。本构模型计算模块首先需要通过x k中的压力和内能计算其他物性参数，然后计算相间换热、相间摩擦、壁面换热等守恒方程中其他项。

图1 程序计算流程Fig.1 Flowchartofthecodecalculation

3 程序验证

3.1 水龙头问题

为了验证数值算法的稳定和精度，数值实验基准题——Ransom水龙头问题［17］被模拟，实验的初始和边界条件如表1所示。

表1 实验初始条件和边界条件Table1 Initialandboundaryconditionofthewaterfaucet test

研究对象为12 m长的竖直向上的圆管，直径1 m，初始时刻圆管内气相份额为0.2，气相速度为0.0 m‧s-1，液相速度为10 m‧s-1，液相温度为50℃，压力为105Pa。在瞬态过程中，进口的空泡分数、液相和气相速度保持不变，出口压力恒定105Pa不变。瞬态过程如图2所示，初始液膜与管壁平行，随着瞬态的进行，由于重力的作用，液相加速下降。在受进口边界条件影响的区域，沿着管壁液相份额不断地减少，而不受进口条件影响的区域，液相做自由落体运动，空泡份额一直保持不变，因此沿着管壁空泡份额不连续。最终液相和气相形成稳态。

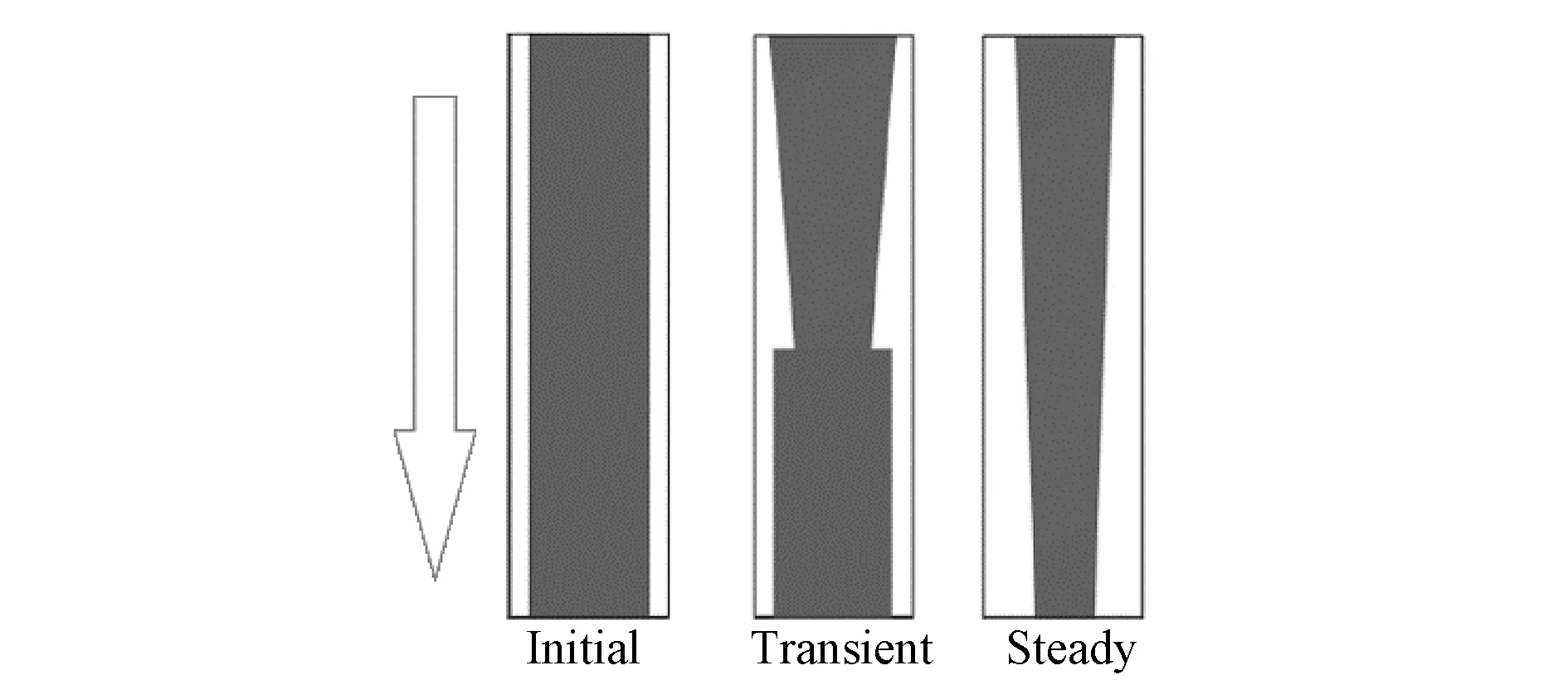
图2 水龙头问题示意图Fig.2 Sketchofthewaterfaucettest

空泡份额和液相速度的解析解为：

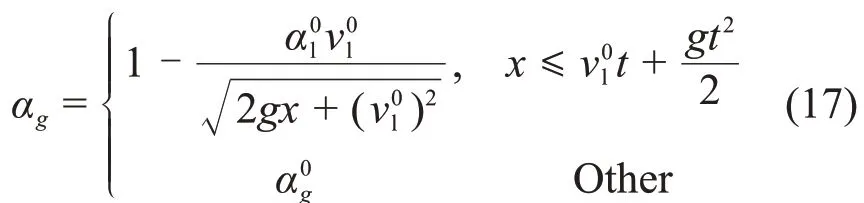
图3展示了瞬态开始后0.5s时程序计算的空泡份额和液相速度与解析解和NUSOL-SYS程序（西安交通大学核安全与运行实验室开发的系统分析程序）计算结果的比较。控制体长度为0.3m，时间步长为0.005s，程序计算值与实验值符合得很好。由于空间离散使用了VanAlbada高阶精度的差分格式，较NUSOL-SYS使用的一阶迎风差分格式，数值耗散更小，因此程序的计算值比NUSOL-SYS程序的计算值更加精确。比较结果证明了当前全隐数值算法的精度比较高，且由于0.5s时空泡份额的分布在0.2~0.5，此时没有液滴夹带产生，该工况的精确模拟也论证了对于某一相或两相缺失的问题而进行的数值处理是合适的。

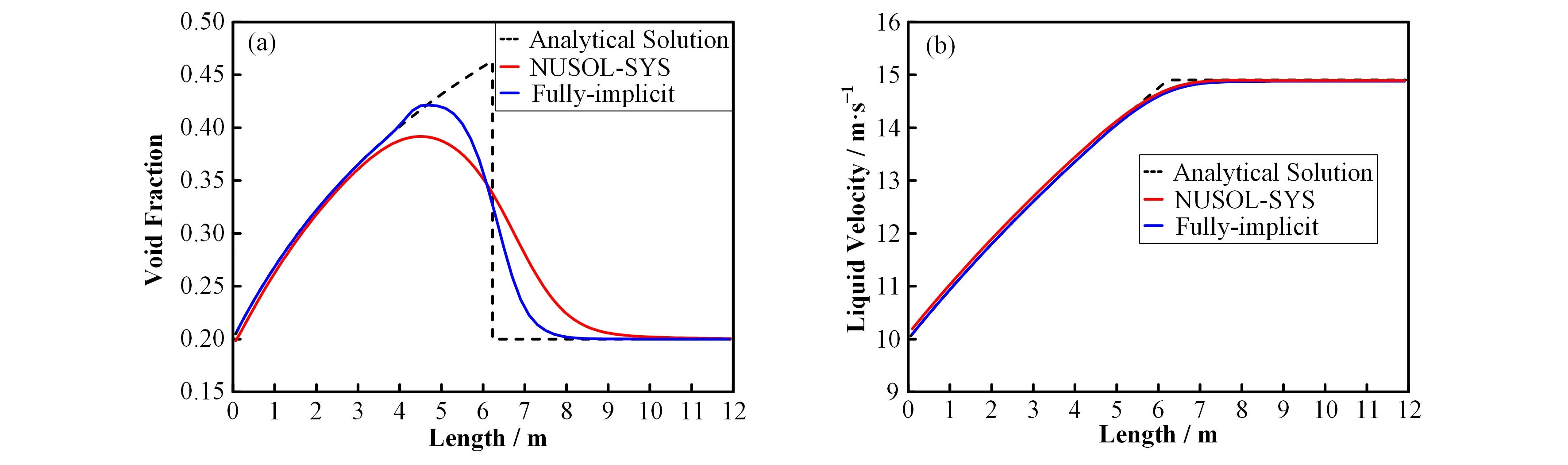
图3 0.5 s时全隐算法计算结果与解析解和RELAP5结果的比较 (a)空泡份额，(b)液相速度Fig.3 Comparison between the predicted results by fully-implicit numerical algorithm,analytical solution and the predicted results by semi-implicit numerical algorithm at 0.5 s (a)Void fraction,(b)Liquid velocity

3.2 Bartolomei过冷沸腾实验

为了评估程序计算单相传热以及单相到两相过渡时的表现，这部分模拟了Bartolomei单管过冷沸腾传热实验［18］，模拟选取了中压中流速中过冷的工况2、中压低流速低过冷的工况5、中压高流速高过冷的工况8以及一组低压的工况22，实验条件如表2所示，为了平衡总的计算时间和Krylov子空间迭代的收敛速度，使得总的计算时间尽可能少，各工况的CFL（CFL=最大相速度×时间步长/网格长度，该值越大，Krylov子空间迭代收敛越慢）值为0.276~0.455。

表2 Bartolomei过冷沸腾实验条件Table 2 Experimental conditions of Bartolomei subcooledboiling experiment

当具有一定过冷度的水进入竖直向上的圆管后，沿着流动方向不断地被加热，当达到过冷沸腾起始点后过冷沸腾发生，沿着流动方向空泡份额的分布如图4所示。基于全隐算法的预测结果与实验值符合的较好，且与之前开发的基于半隐算法的两流体三流场模型的计算结果基本一致，同时由于图4中计算的几组过冷沸腾工况均没有达到环雾流，即没有液滴，而两流体三流场模型在单相、泡状流和弹状流的模型与NUSOL-SYS程序的模型一致，故基于全隐算法的模拟结果也与NUSOL-SYS程序的计算结果符合的很好。此外，结果也论证了当前模型和数值算法在单相、从单相到两相的过渡以及缺少液滴的两相工况都表现的很好。

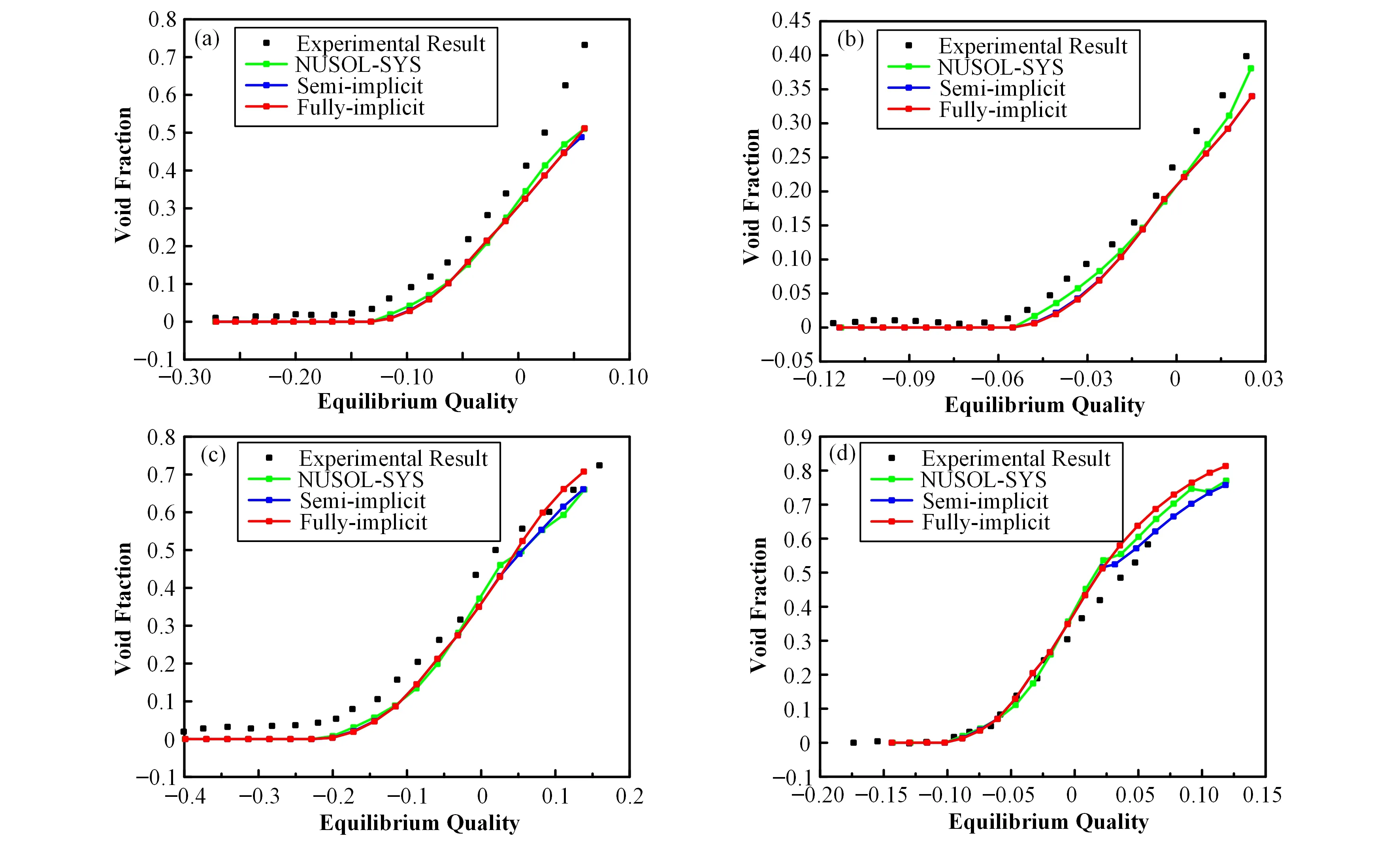
图4 全隐算法计算结果与实验值和NUSOL-SYS、半隐算法结果的比较 (a)工况2，(b)工况5，(c)工况8，(d)工况22Fig.4 The comparison between the predicted results by fully-implicit numerical algorithm,experimental results and the predicted results by NUSOL-SYS and semi-implicit numerical algorithm at 0.5 s (a)Test 2,(b)Test 5,(c)Test 8,(d)Test 22

3.3 Dryout传热实验

为了验证基于全隐数值算法的两流体三流场两相流模型计算弹状流、环雾流、弥散流之间过渡时的表现，Dryout传热实验被模拟。在环状流区域，由于气芯不断地剪切液膜而夹带产生液滴，液膜厚度不断地变小，当液膜厚度减小到临界值以下时，流体不能带走足够的热量，壁面温度飞升，发生沸腾临界现象。模拟选取了Bennett［19］和Becker［20］的实验中两种比较极端的工况，即干涸发生时液滴较多的高流量工况Becker-221、Becker-232和干涸发生时液滴较少的低流量工况Becker-277、Bennett-5358，实验条件见表3。

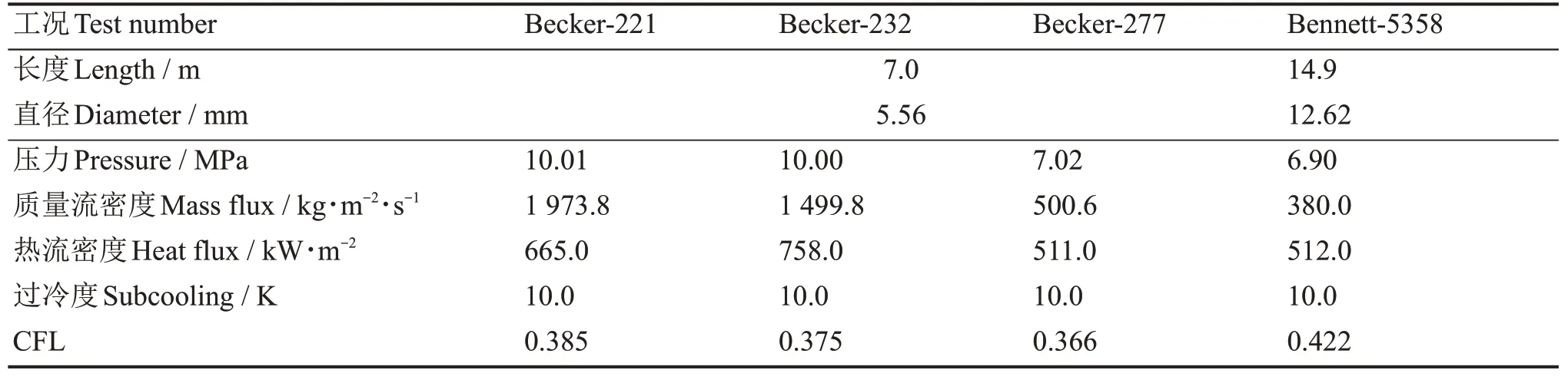
表3 Dryout传热实验条件Table 3 Experimental conditions of dryout experiment

图5展示了4组实验工况沿轴向汽相份额和液滴份额的分布。对于工况Becker-277和Bennett-5358，干涸点对应的汽相份额大于0.99，干涸后区域液滴份额较少，液滴对换热的影响很小，干涸后壁面与蒸汽的对流换热占据壁面传热主要部分。

图5 汽相份额和液滴份额的轴向分布Fig.5 The axial fraction distribution of void and droplet

图6显示了基于半隐数值算法和全隐数值算法的三流场模型计算得到的壁温与NUSOL-SYS程序计算得到的壁温基本相同，且全隐数值算法的计算结果与半隐数值算法的计算结果基本一致。而对于高流量的工况（Becker-221和Bennett-232），干涸发生时汽相份额约为0.9，液滴份额较多，由于弥散的液滴蒸发吸收了很多热量，壁面温度不会一直上升。图7中计算值与实验值比较可以发现，由于液滴的作用，三流场模型计算的壁温比NUSOL-SYS程序计算的壁温更加准确，且液滴的夹带沉降模型以及液滴的相间换热模型是精确的，同样全隐数值算法的计算结果与半隐算法的计算结果基本相同。

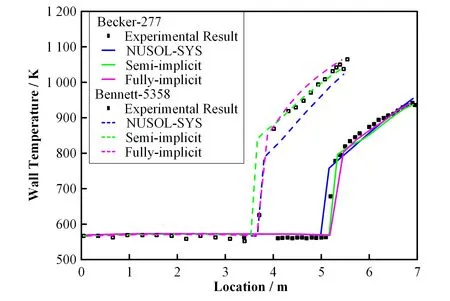
图6 低流量全隐数值算法的计算结果与实验值、NUSOLSYS计算值和半隐数值算法的计算结果比较Fig.6 The comparison between the predicted results by fullyimplicit numerical algorithm,experimental results,simulated results by NUSOL-SYS and the predicted results by semiimplicit numerical algorithm for the conditions with low mass flux

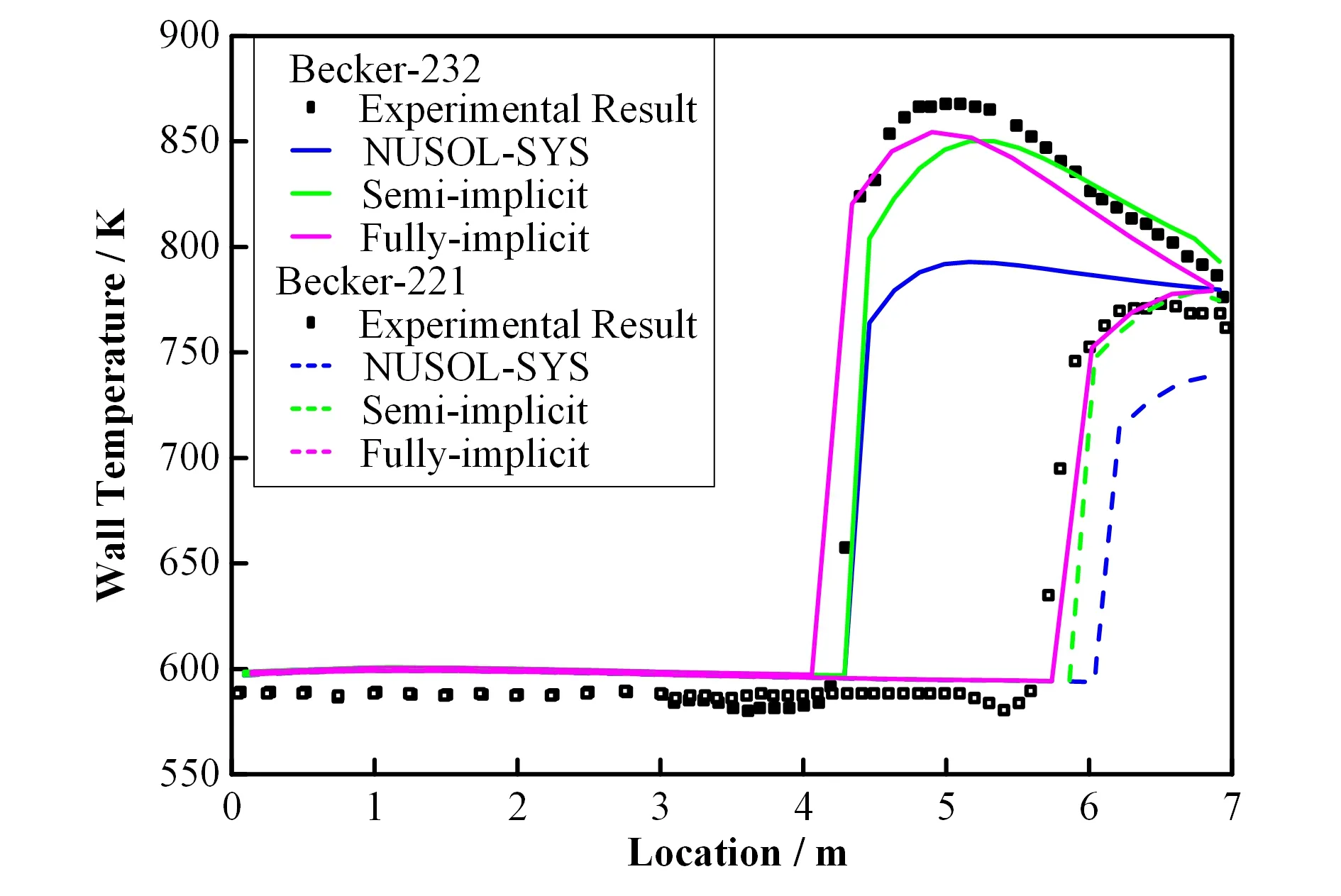
图7 高流量全隐数值算法的计算结果与实验值、NUSOLSYS计算值和半隐数值算法的计算结果比较Fig.7 Comparison between the predicted results by fullyimplicit numerical algorithm,experimental results,simulated results by NUSOL-SYS and the predicted results by semiimplicit numerical algorithm for the conditions with high mass flux

干涸后传热实验的模拟结果也说明了当前开发的两流体三流场模型的全隐数值算法在计算弹状流-环雾流、环雾流-弥散流之间过渡时表现很好。

4 结语

本文针对两流体三流场两相流模型，实现了基于JFNK算法的全隐数值算法，并通过模拟相关实验对数值算法进行验证，得出以下结论：

1）Ransom水龙头数值基准题的模拟结果表明：基于Van Albada高阶精度差分格式的全隐数值算法比NUSOL-SYS程序具有更高的精度，且当前数值算法对单相、没有液滴相的两相数值处理是可行的。

2）过冷沸腾实验的模拟结果表明程序可以成功从单相水过渡到弹状流，空泡份额分布与实验值符合较好，且由于过冷沸腾实验中没有液滴存在，程序计算结果准确性与NUSOL-SYS程序的计算结果相当。同时当前全隐数值算法在单相到两相过渡以及泡状流-弹状流过渡时表现很好。

3）Dryout传热实验的模拟结果表明，两流体三流场模型计算的壁温比传统的两流体模型更加准确，且当前全隐算法的计算结果接近半隐数值算法的精度。数值算法计算弹状流-环雾流、环雾流-弥散流之间过渡时表现很好。

本研究开发的全隐数值算法的核反应堆安全分析程序的发展奠定基础，但为了提高系统分析程序的模拟精度，还需要进一步的研究来改善两相流中一些模型的计算精度，如CHF模型、一些相间传热模型。

作者贡献声明樊杰：模型和算法开发，程序设计，程序验证，文章撰写；吴和鑫：实验数据调研和处理，文章修改；苟军利：论文整体设计，对文章作批评性审阅，研究经费支持；单建强：提供技术指导，对文章作批评性审阅。