四足机器人步态参数优化及探索性行走策略

赵江波，龚思进，王军政

（1. 伺服运动系统驱动与控制工业和信息化部重点实验室，北京 100081；2. 复杂系统智能控制与决策国家重点实验室，北京 100081；3. 北京理工大学 自动化学院，北京 100081）

四足机器人由于其对复杂地形的适应性强，具有轮式和履带式机器人无法比拟的优势. 四足机器人配备不同的工具载荷，可以在各种环境执行任务，如物流运输、安防巡检、灾区救援等.

四足机器人被期望在复杂的环境、有限的能量供应和存在不能预知的干扰下表现出稳定的运动行为. 有几种典型的运动生成方法[1]，如中心模式生成器、神经网络、隐马尔可夫模型、基于模糊逻辑系统以及分析概念的方法. 分析方法是指通过分析特定任务来构造步态. 然而，这种方法在无法感知或变化的环境下会失效. 基于规则和模糊逻辑的方法是通过查找表或某种规则确定的运动，这些运动是通过应用专家知识或学习/优化技术指定的，具有应对不同情况和步态转变的能力.

为了提高四足机器人的运动能力和稳定性，研究人员采取机器学习的方法，例如策略梯度法或遗传算法来优化步态参数[2-4]. JANARDHAN 等[5]考虑机器人的动态平衡，将两足机器人的跨越沟壑任务表述为约束非线性优化问题. GUO 等[6]研究了机器人脚与地面的摩擦、关节执行器扭矩和角速度的限制等因素对机器人的影响. 另外，完成特定任务的能量消耗也是评估机器人运动性能的关键指标之一.ROY 等[7]使用最小化足端力的范数和最小化关节扭矩的范数，估计6 足机器人实时控制所需的能量最佳足端力和关节扭矩. SOYGUDER 等[8]通过模仿蜘蛛来改进6 足机器人的行为，在能量消耗和运动稳定性方面做出改进.

意大利理工的HyQ 团队使用基于二次规划的力分配方法[9]，实现了四足机器人在50°V 型坡内行走，该方法计算出的扭矩不会导致脚部打滑，满足接触力的单边约束并且最大程度地减少了执行器的工作量. ACEITUNO-CABEZAS 等[10]提出了一种混合整数凸规划公式，其中定义了一个同时规划接触和运动的单个混合整数凸优化问题，实现了机器人在步态切换和非共面接触情况下也能保持运动稳定. 波士顿动力公司在DARPA 的自学习机器人项目中开发了Little Dog 四足机器人，许多研究人员基于Little Dog 针对步态策略提出了不同的机器学习算法，其中一些研究人员通过分层的学徒学习实现了复杂地形中的边界运动[11-12]. 为了实现Little Dog 爬楼梯的任务，KOLTER 等[13]使用了差分符号策略梯度法来优化身体的位移.

KOLTER[14]，KALAKRISHNAN[15]和ZUCKER 等[16]使用多层强化学习作为运动规划算法的主要框架.框架包括3 部分工作：生成地形代价成本地图、路径规划和运动规划. 路径规划和运动规划均基于生成的地形代价成本图. KOLTER 等使用视觉捕获系统来获取机器人的位置和地形高度图. 地形代价成本图是从学徒学习和地形高度信息中获得的. 在他们提出的解决方案框架中，对地形信息的感知是将优化应用于路径规划和运动规划的前提.

MIT 的BLEDT 等[17]利用基于有限状态机的接触检测算法，可以检测到与楼梯等障碍物体的意外碰撞，并通过基于事件的步态调度程序将其用于修改足端轨迹和平衡策略. 一旦机器人感应到障碍，它就会调整其姿势，并期望足端接触点落在估计平面.

与之前提及的研究不同，本文关注的是机器人没有通过视觉获得地形信息，而是通过关节扭矩传感器和编码器以及IMU 来感知地形的情况. 本文采用粒子群优化算法(PSO)，以四足机器人的运动速度、稳定裕度、能量消耗和避障能力为目标函数，对步态参数进行优化. 提出了一种包含探索性步态规划和姿态调整的越障行走策略，使机器人能够跨越未知障碍物. 通过仿真验证了所提出的运动策略，在仿真的基础上，本文在四足机器人平台上进行了多个实验，以测试机器人跨越有限尺寸障碍物的能力.

1 四足机器人实验平台

如图1(a)和图2(a)所示，四足机器人实验平台有12 个活动自由度（DOF），每条腿都有一个髋关节外展/内收(HAA)关节，一个髋关节屈伸/伸展关节(HFE)和一个膝盖屈伸/伸展关节(KFE). 所有活动关节由实验室自行设计的轻量式液压缸驱动. 位置编码器嵌入液压缸末端，用于测量液压杆的伸长量，力传感器固定在杆头与腿部的连接位置，用于测量施加在缸杆上的力. 动力由外部油压泵提供. 四足机器人实验平台和仿真模型分别如图1(a)和图1(b)所示.

图1 四足机器人实验平台及仿真模型Fig. 1 Quadruped robot platform and simulation model

机器人的每一条腿有3 个自由度：髋关节2 个自由度，膝关节1 个自由度. 前腿和后腿的结构均以肘形配置. 机器人机械结构参数见表1，参数含义如图2(b)所示.

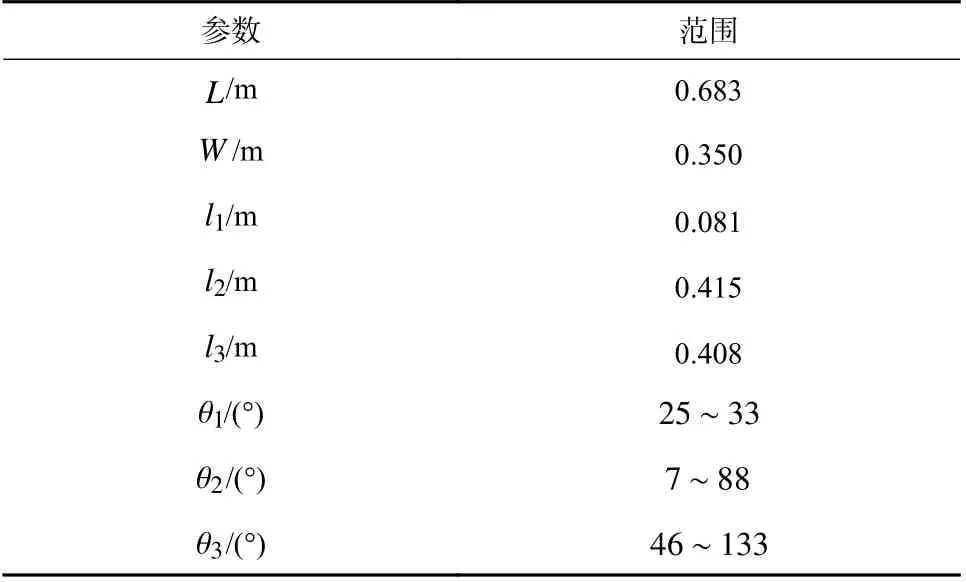
表1 四足机器人机械结构参数Tab. 1 Mechanical structure parameters of quadruped robot

四足机器人的坐标系定义如图2 所示. 建立单腿的正向运动学(FK)和逆向运动学(IK)方程，如式(1)和式(2)所示.

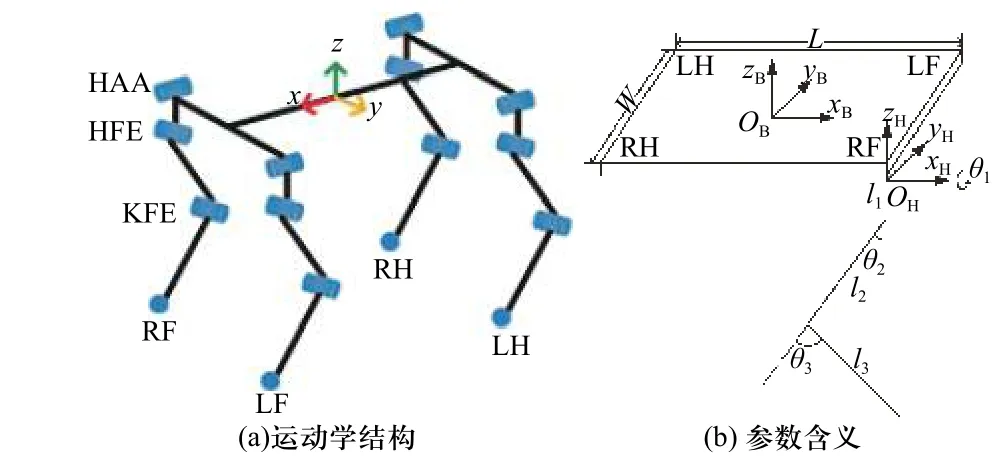
图2 四足机器人的运动学结构Fig. 2 The kinematics of the quadruped robot

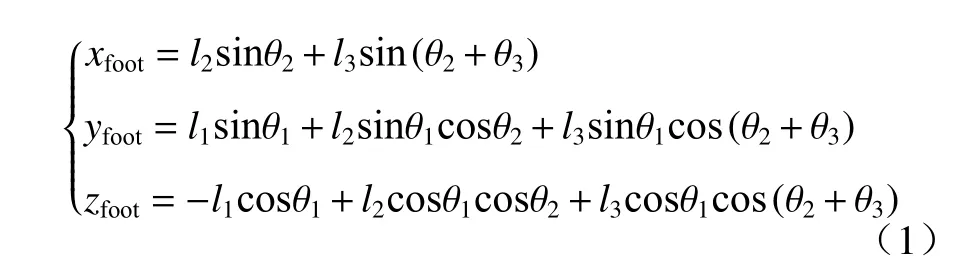
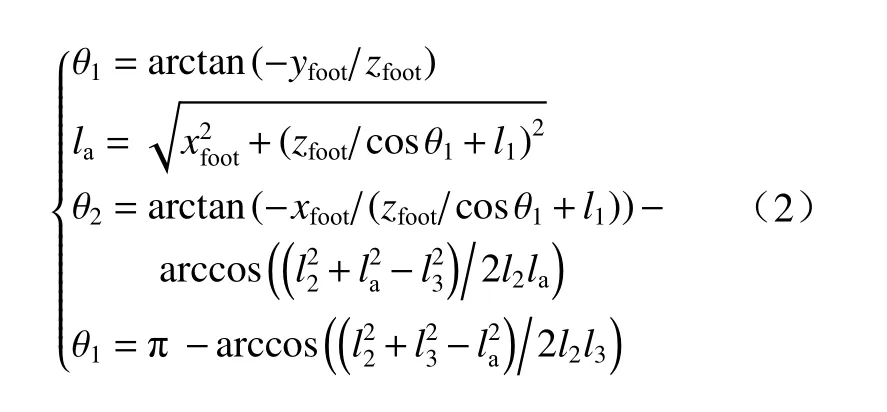
2 探索性步态规划

经典的静步态包括两种运动行为：一种是腿的支撑和摆动运动，另一种是将身体重心移动到支撑三角型区域在水平面上的投影. 经典静步态的整个过程可分为8 个阶段，如图3 所示.

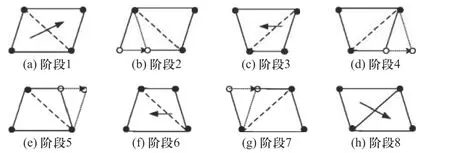
图3 经典步态的8 个阶段Fig. 3 Eight stages of the classic walking gait

如图4 所示，每条腿的步态包括4 个阶段：支撑阶段和第1，2，3 摆动阶段. 支撑阶段的周期用Tsp表示，摆动阶段1，2，3 的周期用Tsw1，Tsw2和Tsw3表示.S为迈步的步长，H为迈步的步高.

图4 机器人平坦地形腿部运动Fig. 4 The robot walks on even terrain

摆动阶段和支撑阶段中每条腿足端的期望轨迹表示如下

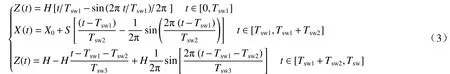
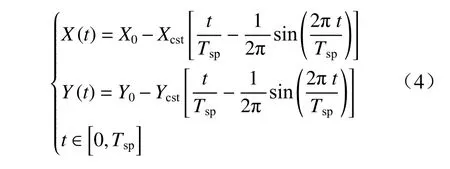
经典的静步态只能保证四足机器人在平坦的地形上行走. 为了弥补这一缺陷，本文提出了一种探索性步态，与静步态相比，足端运动控制采取以下策略：在探索性步态的摆动阶段，判断是否存在障碍物，并跨越有限大小的障碍物.

如图5 所示，在摆动阶段2，当力传感器测得的数值大于预设阈值时，足端接触到障碍物. 然后足端跟踪如图5 所示的设定轨迹. 轨迹跟踪任务又称避障运动，包括两个方向的运动：在X轴方向，足端先缩回；在Z轴方向，足端位置继续上升，直到X轴方向回到原来的位置. 第2 阶段避障动作完成后，脚端继续移动，直到在X轴方向上总共向前移动S距离.如果足端碰到另一个障碍物，将再次进行避障动作.在第3 摆动阶段，摆动腿接触地面或障碍物. 当脚端力传感器测得的数值大于给定阈值时，摆动腿刚好接触到障碍物的上平面，表明整个摆动阶段结束. 如果足端向下移动H距离后没有接触地面，它将以H/Tsw的速度继续向下移动，直到接触到地面，或达到运动极限.

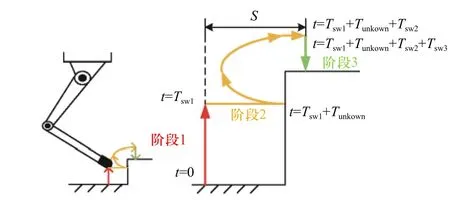
图5 机器人台阶地形腿部运动Fig. 5 The robot walks on rough terrain

与传统的步行步态相比，探索式步态具有以下优点：①利用触觉传感，机器人能够适应复杂的地形；②步态规划相对简单，且不需要随着地形的变化而改变参数S和H.

3 步态参数优化

上一节中介绍的经典静步态和探索性步态都可以视为规划机器人足端和身体质心跟踪参考轨迹.两种步态由规划轨迹形状的几个参数确定，例如步长S、步高H和步态周期T等. 本文选择一些关键参数，并期望找到这些参数的最优值，通过粒子群优化算法实现更好的四足机器人运动性能.

3.1 引入PSO

与其他进化算法一样，粒子群算法需要初始种群和目标函数来评估每个个体的适应度. 粒子群算法的特点是每个粒子个体在搜索空间中都有自己的位置和速度. 位置对应于最高目标函数值的粒子称为最佳粒子，其位置称为最佳位置. 每个粒子的运动都受其局部最佳位置的影响，也会被搜索空间中最佳的位置所引导，最佳位置随着其他粒子找到更好的位置而更新，这将使群体向最佳位置移动. PSO 算法可表示为

3.2 约束条件和目标函数

关节位置和关节旋转速度的运动学极限可以转化为步态参数空间中的约束. 需要步态参数来满足两个运动学极限，约束条件由式(6)表示

每个步态周期的能量消耗可以看作是身体和4条腿的运动学能量变化的总和，摆动相的足端运动速度如图7 所示. 需要注意的是认为机器人的重力势能在运动中保持不变. 可以用式(9)表示步态参数与每个步态周期的能量消耗之间的简化关系mbase的比率为0.25，能量消耗的目标函数化为式(10)

图6 稳定裕度定义Fig. 6 Stability margin

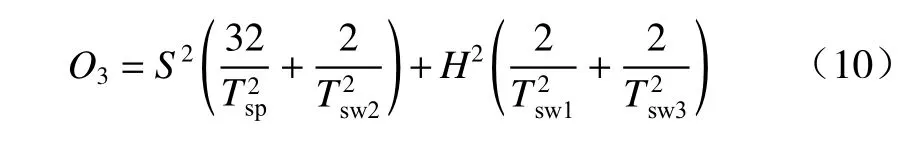
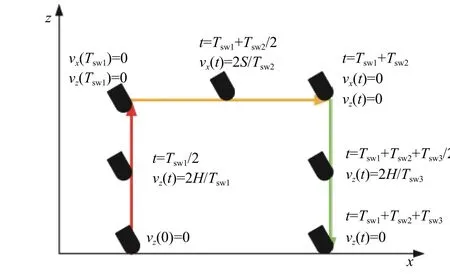
图7 摆动相的足端速度Fig. 7 The velocity of foot end in the swing phase

可以用步态轨迹在x-z轴平面形成的形状面积来评估避开障碍物的能力，越障能力目标函数表达为式(11)

3.3 PSO 的实施

优化的步态参数由每个粒子的位置表示. 经典的步行步态有4 个参数需要优化：步长S、步高H、步态周期T和机身的高度Dh，参数范围限定如表2所示，初始粒子群的生成算法如图8 所示.

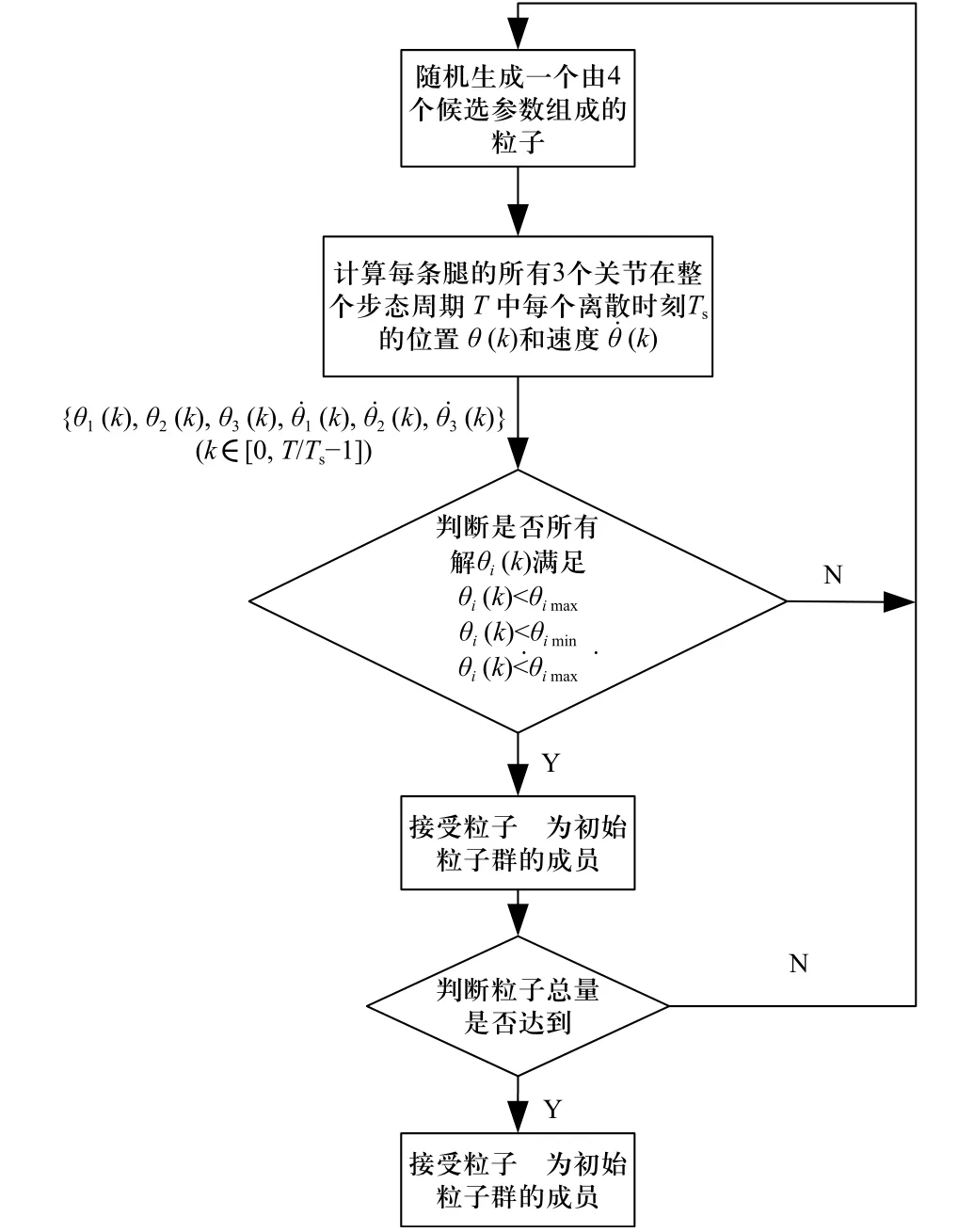
图8 PSO 初始种群粒子的产生Fig. 8 The generation of initial population of PSO

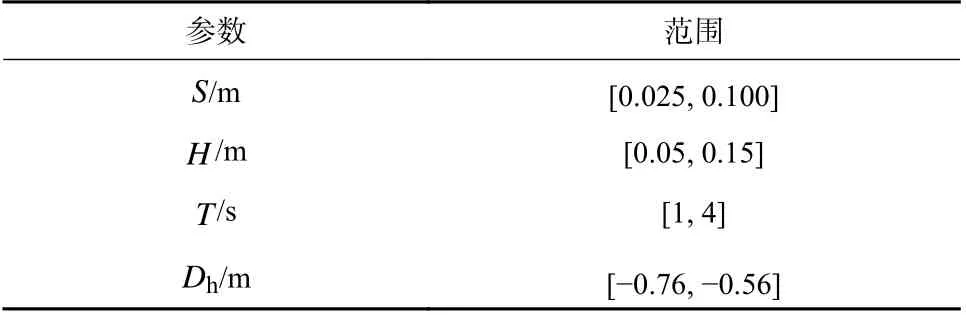
表2 步态参数范围Tab. 2 Range of Gait Parameters

通过离线仿真在每个采样周期中计算与给定步态参数组相对应的关节位置和关节速度. 如果所有求解值都在规定范围内，则该组参数将被视为初始粒子群成员. 重复该过程，直到完成初始粒子的生成为止.

4 姿态调整策略

机器人在运动过程中需要根据当前地形调整机身姿态，姿态调节应该为下一个摆动腿的运动提供更多的操作空间，同时保持机器人的稳定性.

利用激光雷达和立体视觉组成的环境感知系统是获取地形信息的一种直接方法，可以根据环境数据来估计机器人所处的地形[18-19]，一般情况下这种方法会导致估计的地形与实际地形之间存在较大的误差. 本文将IMU 传感器数据与机器人足端在机身基坐标系下的实时位置相结合，对当前地形进行估计.

机器人姿态调整方法表述为

假设机器人刚刚完成一次左前摆动足的运动，并准备好将身体质心投影移动到下一个支撑三角形内并调整姿势. 如图9(a)所示，ΔP2P3P4表示是当前的支撑三角形区域；ΔP1P2P4表示下一步的支撑三角形区域；n0和ng分别为惯性坐标系下ΔP2P3P4和ΔP1P2P4的法向量；O0为当前质心位置在水平面上的投影；Od为在目标质心位置在水平面上的投影.

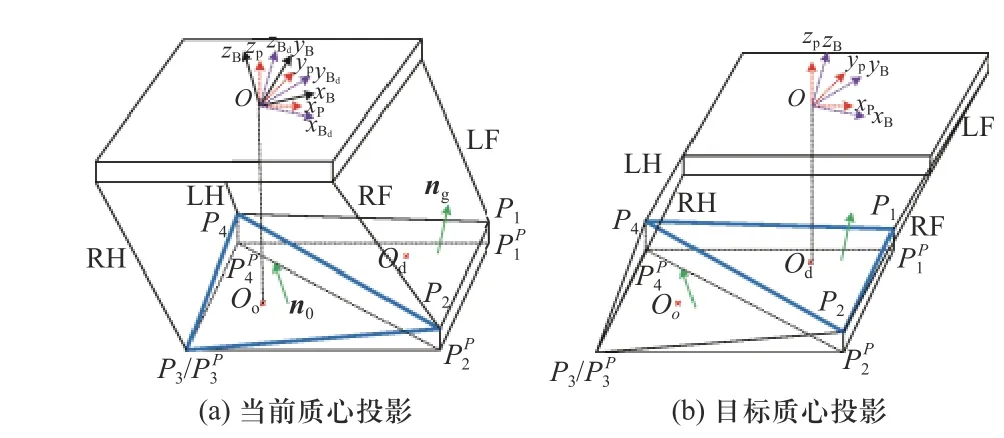
图9 适应地形的姿态调整策略Fig. 9 The pose adjustment strategy to adapt to the terrain

5 仿真和实验结果

本节使用上文说明的粒子群优化算法来优化步态参数，并给出探索性步态策略的仿真结果，图10描述了仿真环境中机器人越过障碍物的过程. 进一步在四足机器人实验平台上进行实验，通过实验验证了该方法的有效性，实验平台和障碍物如图11 所示.在应用PSO 进行迭代计算过程中，主要关注机器人稳定裕度和行走速度及距离. 如图12 所示，总目标函数值、速度目标函数值和稳定裕度值随着迭代次数增加而增加并趋于稳定，速度目标函数值在大约7 次迭代后接近最大值，而稳定裕度值在大约30 次迭代后收敛到最大值. 总目标函数值经过约30次迭代后达到其全局最大值，并基本稳定. 图13 所示第29 次迭代时得到的全局最优步态参数，机器人在固定的仿真时间内跑得最远，同时在稳定裕度上保持了最好的性能. 注意机器人总是会向后移动小段距离，这是因为需要在摆动腿运动后将身体重心移动到下一个支撑三角形区域内.机器人在障碍物上行走的仿真结果如图14 所示，足端轨迹绘制出了障碍物的大致轮廓. 此外可以看到，当机器人在摆动相的不同阶段检测到触及障碍物时，机器人会执行不同的避障动作：①在摆动阶段2 检测到障碍物时，机器人的腿会执行躲避障碍物的动作；②在摆动阶段3 检测到障碍物时，机器人的腿将执行站立动作.基于仿真结果在实验室四足机器人平台进行实验，当四足机器人跨过障碍物时，在机身几何中心高度不变的情况下，足端在髋部坐标系下的z轴位置可推算出于障碍物高度的变化量，因此z轴位置曲线可以反映出障碍物的粗糙形状. 然而由于姿态调整的影响，机身的中心不能保持不变，需要根据调整后姿态做出补偿，实验结果如图15 所示. 当感应到足端的冲击力大于预设阈值时，机器人分别对应摆动相的不同阶段采取避障或站立动作. 结果验证机器人可以较好的通过障碍物地形，并且在权衡速度、稳定裕度、能量消耗、避障能力等多个方面实现了综合的优化提升效果.

图10 障碍物跨越仿真Fig. 10 Obstacle crossing in simulation environment

图11 四足机器人实验平台和障碍物Fig. 11 The robot and the obstacle in the experiment

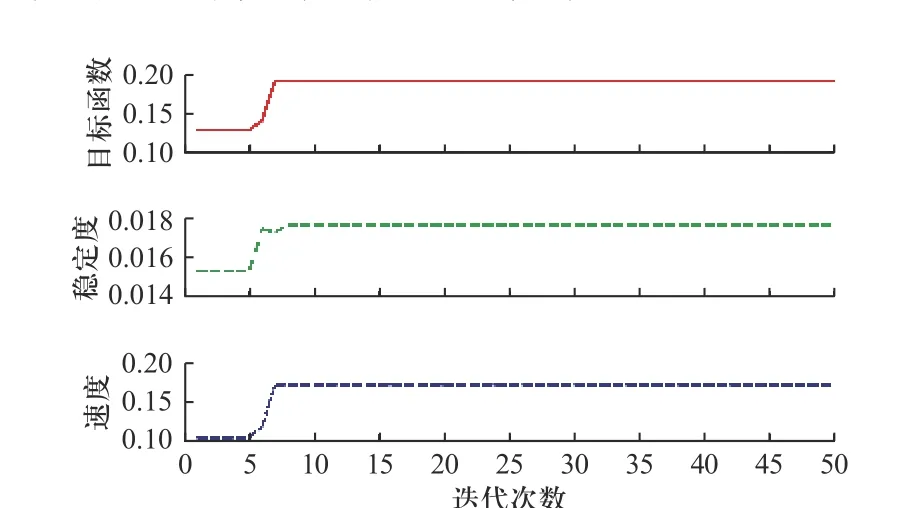
图12 迭代中的目标函数收敛过程Fig. 12 The objective functions versus the iteration

图13 稳定裕度的仿真结果Fig. 13 The simulation result of speed and stability margin

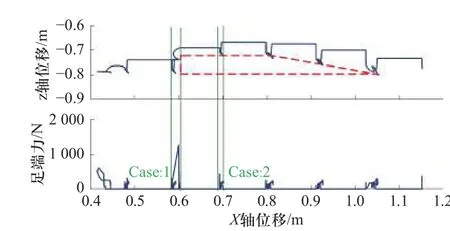
图14 越过障碍物的仿真结果.Fig. 14 The simulation result of walking over the obstacle.

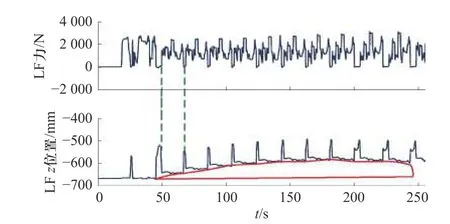
图15 机器人越过障碍物的实验结果Fig. 15 The experiment result of the robot walking over the obstacle

6 结 论

本文采用粒子群优化算法，以四足机器人的运动速度、稳定裕度、能量消耗、避障能力为优化目标，对经典步行步态参数进行优化，并提出了一种探索性的静步态策略，包括跨越障碍的步态规划方法和姿态调整策略. 为了验证该策略在跨越有限尺寸障碍物的能力，进行了多个仿真和实验. 结果表明，探索性步态和姿态调整策略提高了机器人和对未知复杂地形的适应能力.