微齿轮齿面磨损行为及仿真分析
2022-04-23魏沛堂刘怀举朱才朝
魏 东,魏沛堂,刘怀举,朱才朝
(重庆大学 机械传动国家重点实验室,重庆 400044)
微型齿轮作为微机电系统(micro-electro-mechanical system,MEMS)中的重要组成部分,其模数范围通常在0.1 mm及以下,具有传动比大、质量轻和结构紧凑等特点,能够实现微小空间要求下运动和动力的传递[1],广泛应用于航空航天、生物医学、通讯等领域[2]。随着微机电系统的飞速发展,微齿轮需求不断扩大,微齿轮的重要性日益凸显。
随着微齿轮需求的不断增加,微齿轮制造技术得到了长足的发展,目前,有关微齿轮的研究主要集中在加工制造方面。Chinn等[3]利用LIGA技术成功制备直径0.264 mm的镍及镍合金材料微齿轮;Wang等[4]利用改进的微细电火花加工技术,精确制备了模数0.1 mm的金属微齿轮;Loh等[5]利用金属粉末注射成型技术成功制备了模数0.08 mm的微齿轮。除此以外,激光烧蚀[6]、微磨料水射流[7]等先进成型技术也被应用于微齿轮加工。随着微齿轮制造技术的发展,微齿轮服役性能的相关研究也逐渐发展起来。Ali等[8]对比了传统电火花与微细电火花加工对微齿轮尺寸精度及表面粗糙度的影响,发现微细电火花技术能够有效提升微齿轮的尺寸精度同时还能降低表面粗糙度。Wang等[9]针对微齿轮的微观接触特性展开研究,分析了其接触啮合过程中的能量转换及耗散。Zhang等[10]采用表征试验研究微齿轮疲劳失效原因,发现齿面磨损是引起疲劳失效的原因之一。微齿轮副摩擦磨损性能是影响整个系统传动的关键问题。
在微齿轮摩擦磨损行为及其机理研究方面,国内外学者开展了相关试验研究工作。Niza等[11]利用自主开发的微齿轮啮合试验平台,对模数0.065 mm的SK4钢和金属玻璃材料微齿轮进行了干摩擦条件下的啮合传动试验,结果表明齿面的过度磨损导致了微齿轮传动失效,并指出渐开线微齿轮啮合原理同样遵循宏观渐开线齿轮啮合理论。Ishida[12]等对油润滑条件下的直径2.4 mm微型电机进行了寿命试验,发现微型电机内部的微齿轮齿面过度磨损是导致整个传动系统故障的主要原因。日本木更津工业大学高桥秀雄团队[13-15]利用自主搭建的微齿轮耐久性能试验台,对模数0.1 mm的金属微型齿轮开展了耐久性试验,对比了不同工况下的微齿轮失效形式,发现齿面磨损是引起传动失效的主导因素。在微齿轮的摩擦磨损理论研究方面,Hegadekatte[16]等通过微销盘、微双盘摩擦磨损试验获得的微尺度下的滑/滚磨损系数,并利用基于Archard磨损公式开发的全局增量模型(GIWM)进行了微行星轮系磨损仿真,结果表明磨损最严重的位置发生在节线以下,节线处磨损最小,同时磨损会引起啮合线的偏离,对微齿轮的长期运转性能有着重要影响。重庆大学石万凯、王旭等[17-18]采用经典Archard磨损公式,结合JKR理论及GW粗糙度模型,建立了考虑表面形貌的微齿轮磨损数值仿真模型,并提出了改善微齿轮齿面磨损的方法。已有的相关研究得到了微齿轮的磨损失效形式,但是其微观磨损机制尚不明确,同时针对磨损仿真,磨损演化、材料性能及配对等因素影响也不明确。
针对微齿轮磨损失效问题,笔者采用一种自适应有限元方法,基于Archard磨损模型,利用ABAQUS二次开发UMESHMOTION子程序并结合ALE自适应网格技术,建立了微齿轮齿面磨损有限元模型。考虑接触齿面间的相互磨损作用,研究了微齿轮齿面磨损分布规律,分析了材料性能及材料配对方式对其磨损分布及大小的影响,并借助相关试验验证了微齿轮磨损分布规律。
1 有限元仿真方法
1.1 研究对象
为进行微齿轮磨损行为及仿真研究,以深圳兆威机电有限公司生产的微齿轮作为研究对象,该微型齿轮具备大批量生产优势,主要应用于智能手机摄像头升降减速机构(图1(a))。该微齿轮通过金属粉末注射技术(metal powder injection molding,MIM)成型,通过将微米级金属粉末颗粒按一定配比与黏结剂均匀混合,制备出具有流变特性的喂料,然后利用注塑机将喂料注入微齿轮模具成型出微齿轮毛坯,最后将毛坯进行脱脂(脱除黏结剂)、烧结,最终成型出高致密度微齿轮。微齿轮材料为铁镍合金,主要成分如图1(b)所示,其几何与材料性能参数如表1所示。

表1 微齿轮几何与材料性能参数
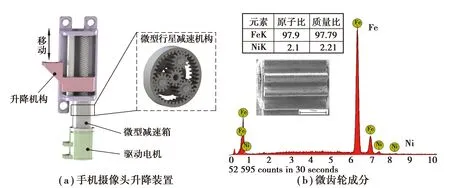
图1 手机摄像头升降装置及微齿轮样品成分Fig. 1 Mobile phone camera lifting device and micro gear sample composition
1.2 Archard磨损模型
笔者建立了Archard磨损模型以进行微齿轮磨损仿真分析。基于物体表面接触是多个表面微凸体接触作用的假设[19],经典Archard磨损理论是从微观角度出发提出的一种磨损理论,广泛应用于中大模数齿轮等为代表的宏观元件的磨损分析[20-22],以及微型齿轮[16]、微型轴承[23]和微型枢轴[24]等的磨损分析。Hegadekatte等[16]基于Archard磨损模型开展了微齿轮磨损分析,磨损量预测结果与试验结果吻合良好。经典Archard磨损公式基于接触应力及相对滑动距离是影响接触面磨损的主要因素的假设,可描述为
(1)
式中:V为磨损量,mm3;W为接触法向力,N;H为磨损材料的表面硬度,N/mm2;s为滑动距离,mm;K为接触面量纲为一磨损系数。将其应用于小局部面积区域磨损,公式(1)可描述为
h=kps,
(2)
式中:h为磨损深度,mm;k=K/H为有量纲磨损系数,mm2/N;p为接触压力,MPa。文中采用文献[16]在微齿轮研究中通过滑滚实验获得的微尺度下的磨损系数k=13.5×10-9mm2/N。
在磨损有限元分析中,将连续的磨损过程离散化,即将整个磨损过程分成多个磨损增量的累积,同时假设齿面接触磨损过程中,在每一个非常小的增量步中,接触点处的压力和磨损系数被认为是一个常数,即节点i的磨损深度为
hi,n=hi,n-1+kpi,nΔsi,n,
(3)
式中:hi,n为节点i在第n个增量步的磨损总深度;hi,n-1为节点i在第n-1个增量步的磨损总深度;pi,n为节点i在第n个增量步的接触压力;Δsi,n为节点i在第n个增量步的相对滑动位移增量。考虑到节点发生磨损后,网格需要重画会提高计算时间成本,为了降低计算代价,假设在ΔN次啮合周期内,每个啮合周期内的磨损量都是相同的,则节点i在经历ΔN次啮合周期后,其总磨损深度为
hi,n=hi,n-1+ΔNkpi,nΔsi,n。
(4)
1.3 磨损面几何特征更新
利用ABAQUS有限元软件进行磨损仿真时,通过移动接触节点来描述磨损行为。接触节点的移动量由Archard磨损公式计算得到,移动方向可由用户自定义,默认为接触法向。两者均通过ABAQUS中的UMESHMOTION用户子程序实现。当接触节点移动量过大时,如图2所示,会出现网格畸变、甚至负体积现象,进而影响有限元结果。因此,需要对这些单元重画网格。网格重画过程是利用ABAQUS中ALE(arbitrary lagrangian-eulerian)自适应网格技术实现。ALE自适应网格技术结合了纯拉格朗日和欧拉算法特征,能够使网格脱离材料而独立流动,在不改变网格原有拓扑的情况下,保证分析过程中的网格质量[25]。
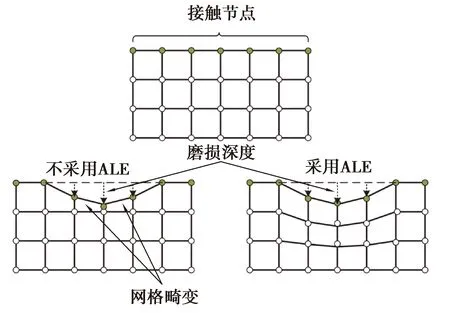
图2 ALE自适应网格技术Fig. 2 ALE adaptive mesh technology
1.4 磨损仿真流程
通过开发ABAQUS UMESHMOTION磨损子程序并结合ALE自适应网格技术实现微齿轮齿面磨损仿真。图3为磨损仿真流程图。在解决非线性接触问题后,UMESHMOTION子程序根据求解后的初始有限元模型访问接触点信息并记录节点接触压力、节点相对滑动位移及节点坐标等数据,然后根据Archard磨损公式计算磨损深度和方向。在每个增量步计算结束后,将计算值应用于该节点的移动,然后通过ALE自适应网格技术进行网格重画并更新磨损面几何特征。在下一个磨损周期里,记录新的接触面各节点的状态变量,重新开始计算,直至整个磨损周期结束。
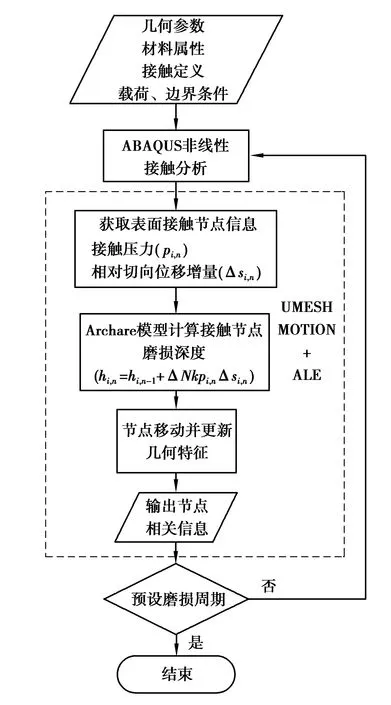
图3 磨损仿真流程图Fig. 3 Flow chart of wear simulation
1.5 有限元模型

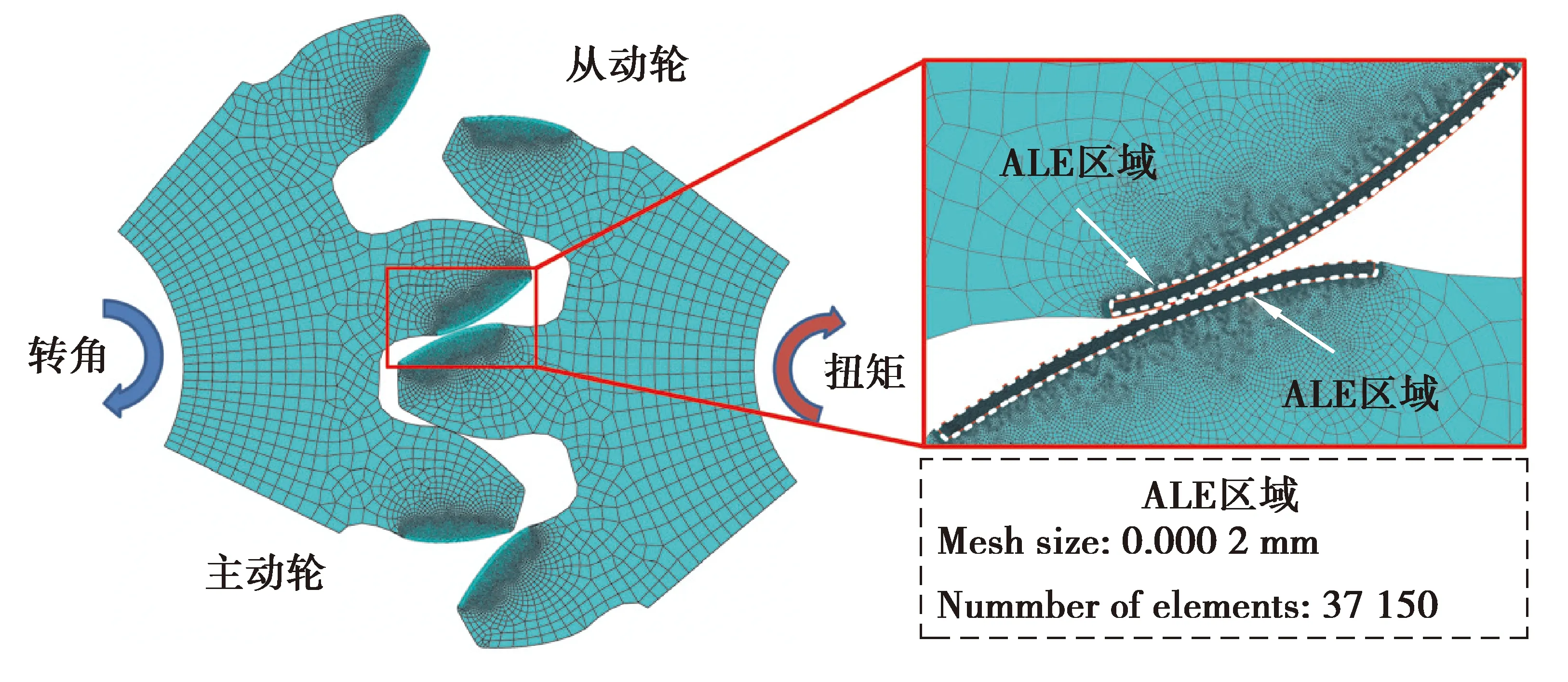
图4 微齿轮磨损有限元模型Fig. 4 Finite element model of micro gear wear
为实现主、从面的相互磨损作用,采用对称主从面方法,同时在进行磨损分析前,对预设磨损区域设置为ALE区域并添加相应约束。为了降低计算成本,文中只考虑中间齿轮对的磨损情况。为保证计算结果可靠,对接触区域进行了网格细化,考虑到网格单元的适应性,选择CPE4平面单元,细化区域网格大小为0.000 2 mm,数量为37 150个。
2 结果与讨论
2.1 齿面接触压力及相对滑动位移分布

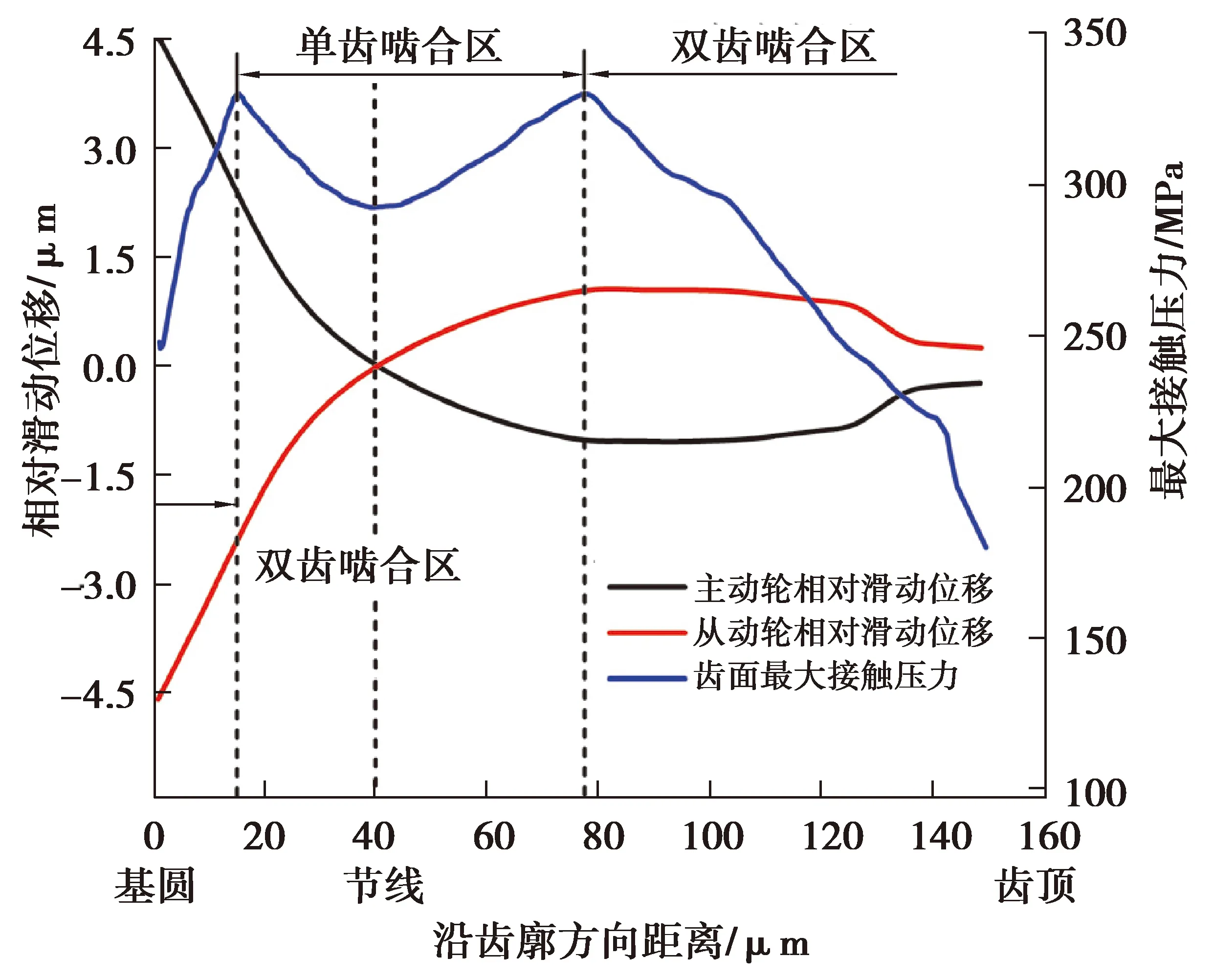
图5 齿面接触压力和相对滑动位移分布Fig. 5 Tooth surface contact pressure and relative sliding displacement distribution
2.2 齿面磨损分布及验证
2.2.1 微齿轮齿面磨损分布
图6,7分别表示不同磨损循环次数下微齿轮主、从齿面磨损深度分布。可以看到,随着循环次数的累积,磨损深度逐渐增加。同时主、从齿面磨损最严重的地方均出现在靠近齿根的基圆附近,8 000次循环后磨损深度最大值约为0.06 μm,其次是单双齿啮合过渡区位置,节线位置磨损深度几乎为0。在微齿轮啮入啮出过程中,靠近齿根的基圆附近具有较大的接触压力以及相对滑动位移(图5所示),进而使得磨损深度最大值出现在基圆附近,相应地,尽管节线位置存在着一定的接触压力,但由于滑动距离几乎为0,所以磨损深度也几乎为0。
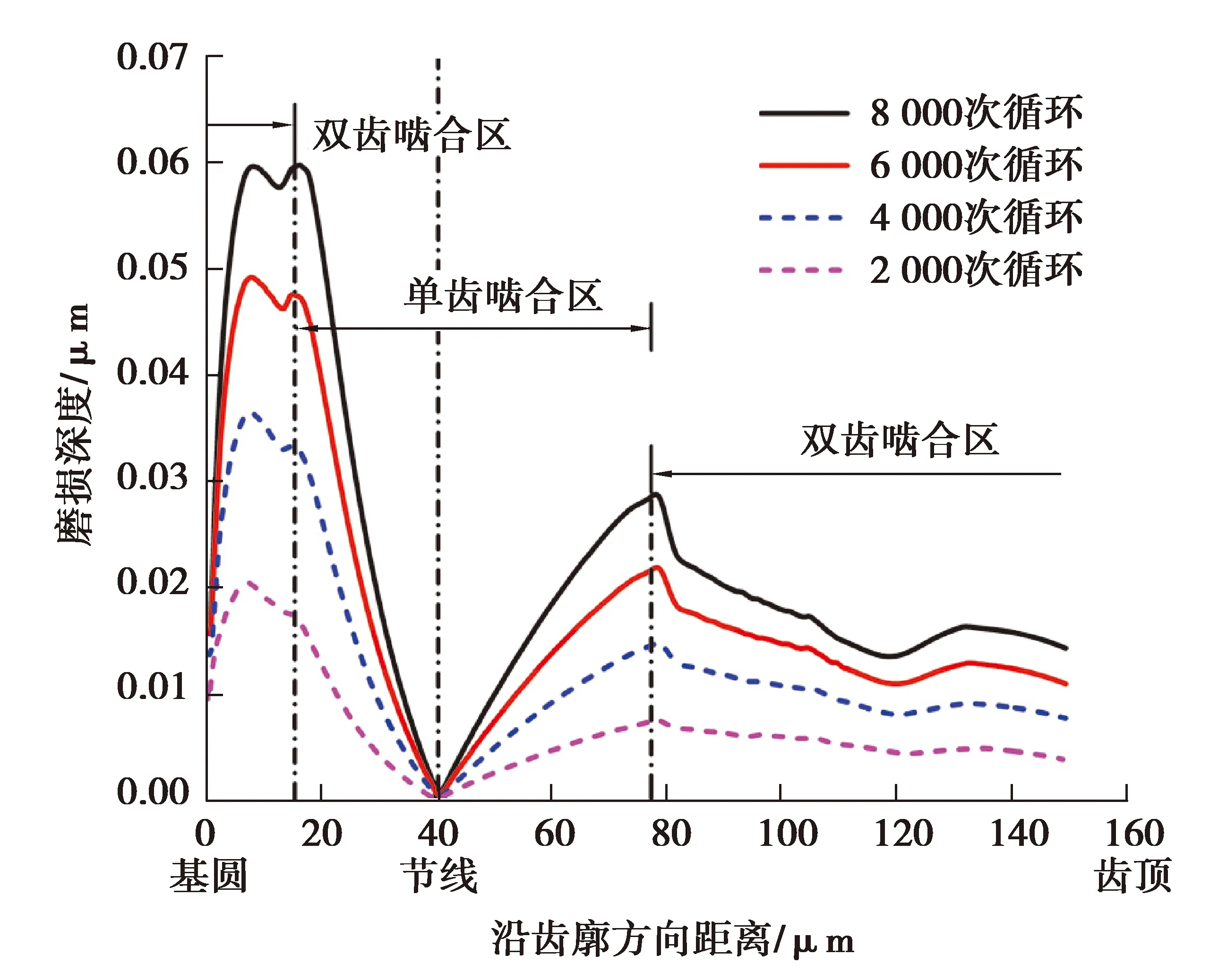
图6 主动轮齿面磨损分布Fig. 6 Wear distribution of driving gear tooth surface
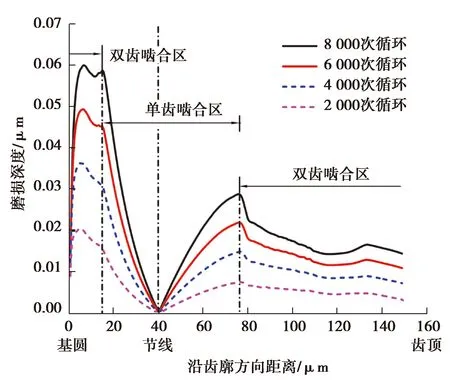
图7 从动轮齿面磨损分布Fig. 7 Wear distribution of driven gear tooth surface
图8表示的是微齿轮主、从齿面最大磨损深度变化。可以看到,主、从齿面最大磨损深度大小及变化基本一致,最大磨损深度并非随着循环次数的增加而线性增加,其斜率(磨损速率)随着磨损循环次数的增加而缓慢降低。这和Brauer等[22]在宏观齿轮磨损分析中得到的结果类似,齿面磨损可能会改善齿面的接触情况,进而降低其磨损速率。
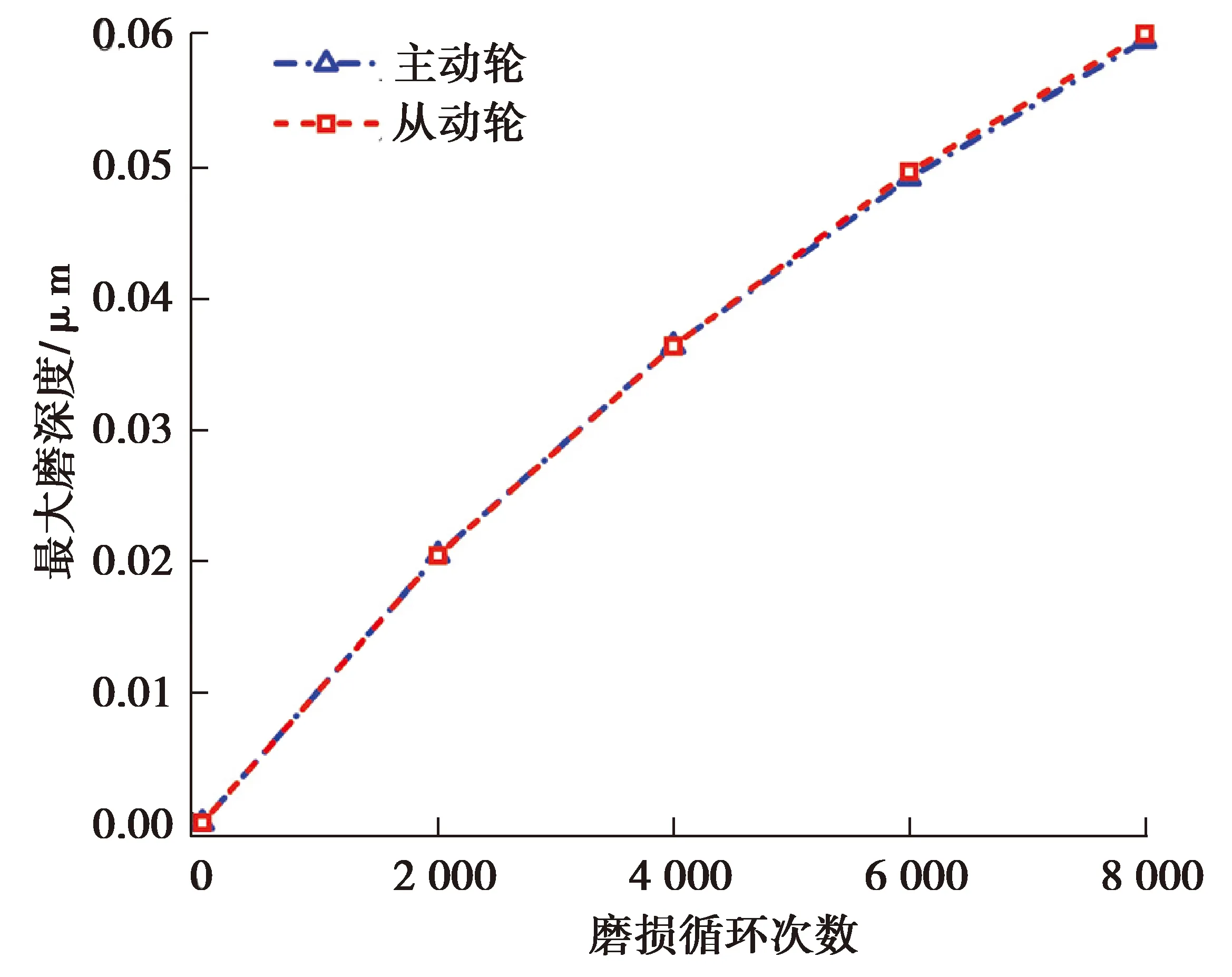
图8 主、从齿面最大磨损量变化Fig. 8 Changes in the maximum wear of the master and slave tooth surfaces
2.2.2 微齿轮齿面磨损试验表征
为了验证微齿轮磨损有限元模型的正确性,将微型减速箱中服役后的微型齿轮进行了齿面SEM检测。微减速箱在服役时,会添加润滑脂以改善其接触状况,因为润滑脂量极少,文中暂未考虑润滑脂的影响。利用Phenom XL台式扫描电镜(图9)对超声波酒精清洗后的微型齿轮进行齿面观察,观察结果如图10所示,可以明显看到,齿顶附近和靠近齿根的基圆附近均发生了不同程度的磨损,且靠近齿根的基圆附近磨损程度大于齿顶附近磨损程度,这和仿真结果得到的磨损分布规律具有相似性。在齿顶附近(图10(b)),可以看到存在较多的磨痕,在靠近齿根的基圆附近(图10(a)),存在着显著的材料流动,表现出黏着磨损特征,这和Ishida等[12]在金属玻璃材料微齿轮摩擦磨损试验中观察到的现象类似,同时周边也存在着磨痕。微齿轮在啮合传动过程中,齿面粗糙峰处于反复的滑滚作用,进而形成磨粒磨损,由于齿根附近接触压力大,同时啮合的微齿轮副是同种材料,齿根附近齿面更易出现材料黏着现象,进而产生黏着磨损。

图9 微齿轮齿面SEM检测Fig. 9 SEM inspection of micro gear tooth surface
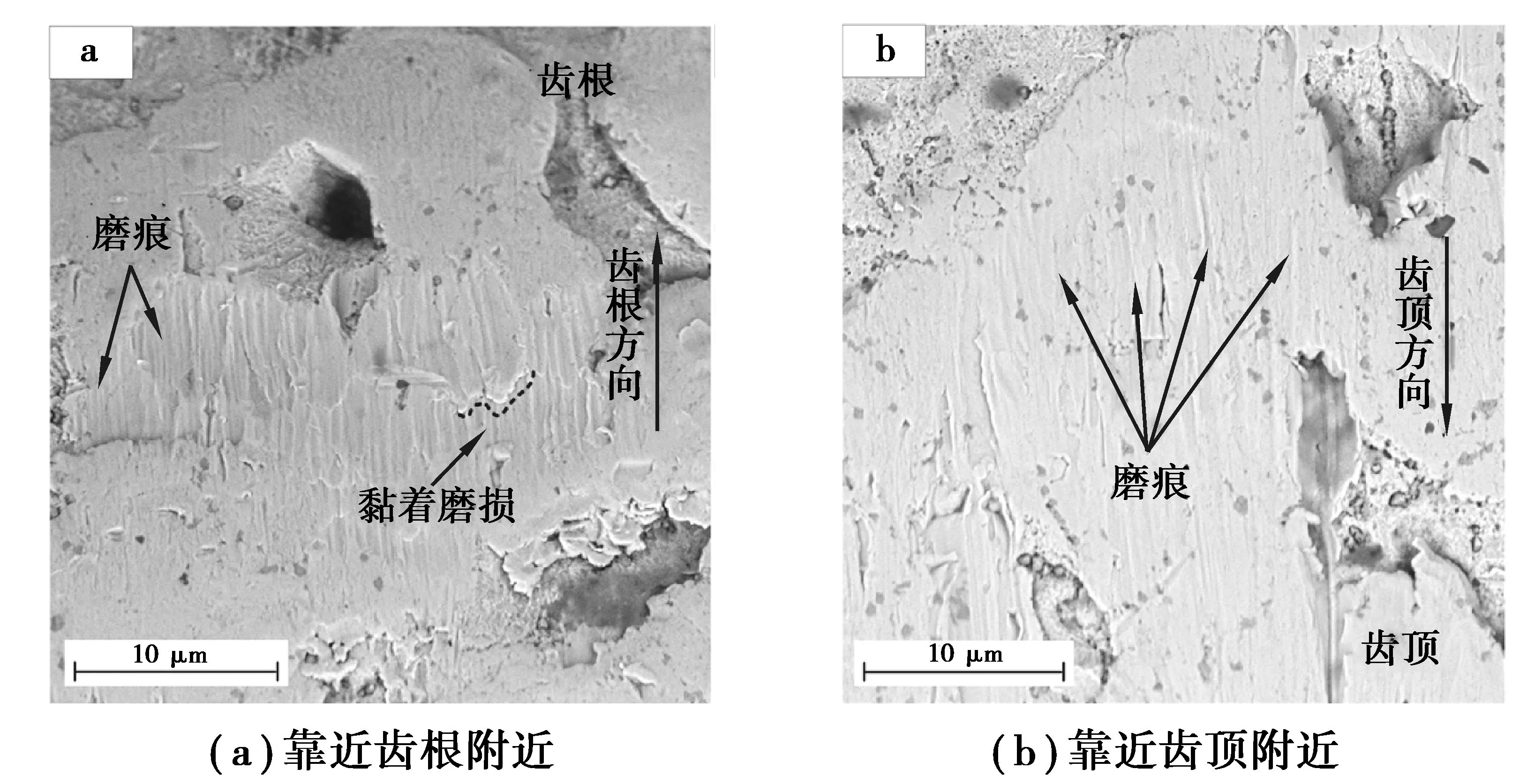
图10 微齿轮齿面不同位置处的磨损Fig. 10 Wear at different positions of the micro gear tooth surface
2.3 参数影响
2.3.1 不同弹性模量下齿面磨损分布及大小
为分析材料性能对微齿轮齿面磨损分布及大小的影响,选择3种铁镍合金材料,弹性模量分别为125,119,100 GPa[18]。从图8,9可以看到,随着材料弹性模量的增大,经过2 000次磨损循环后,微齿轮齿面磨损虽有所减轻但效果不明显,即微齿轮在实际工作中,选择不同弹性模量的铁镍合金材料对其磨损程度并不会有显著影响。
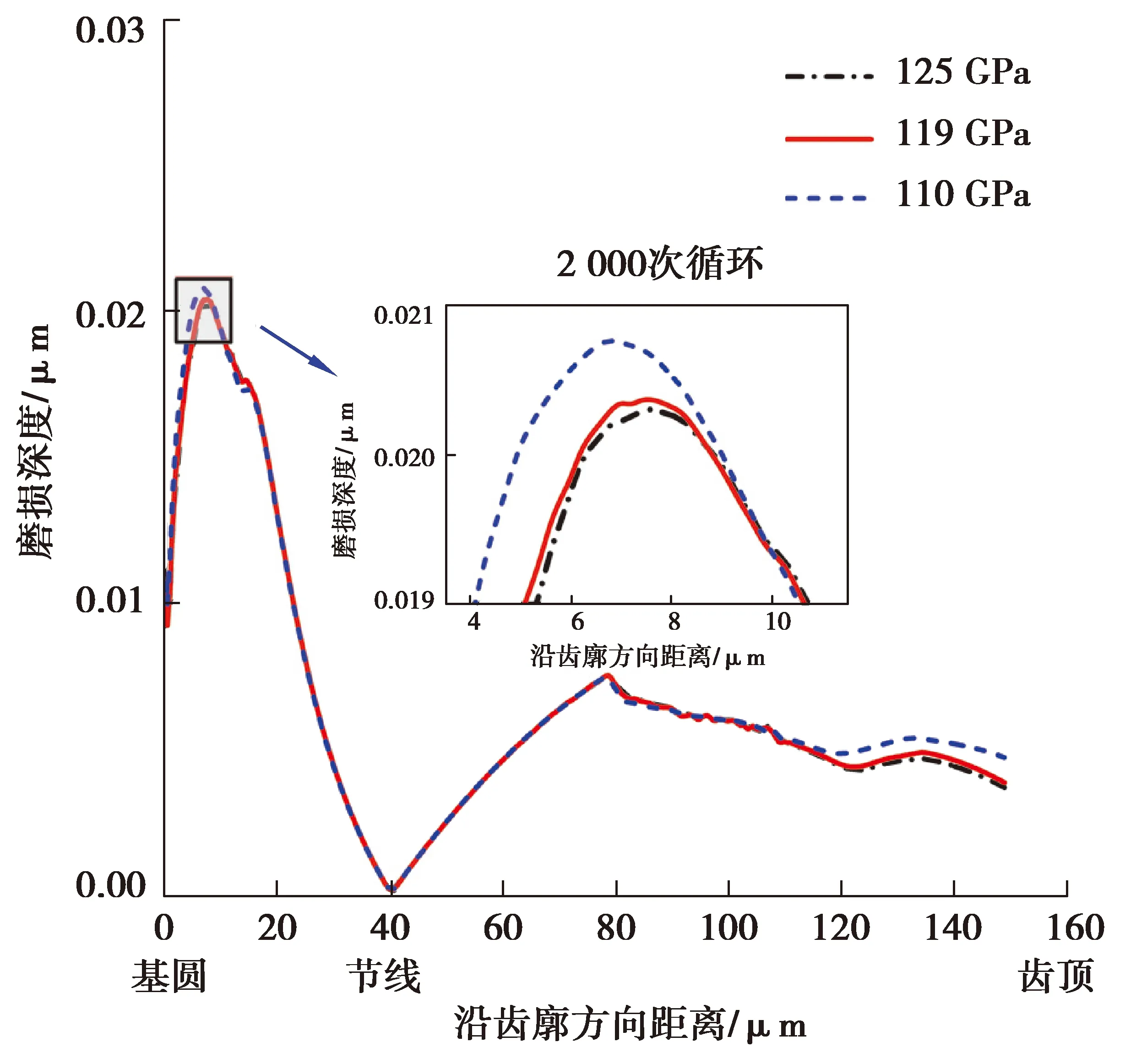
图11 不同弹性模量下主动轮磨损分布Fig. 11 Wear distribution of driving gear under different elastic modulus
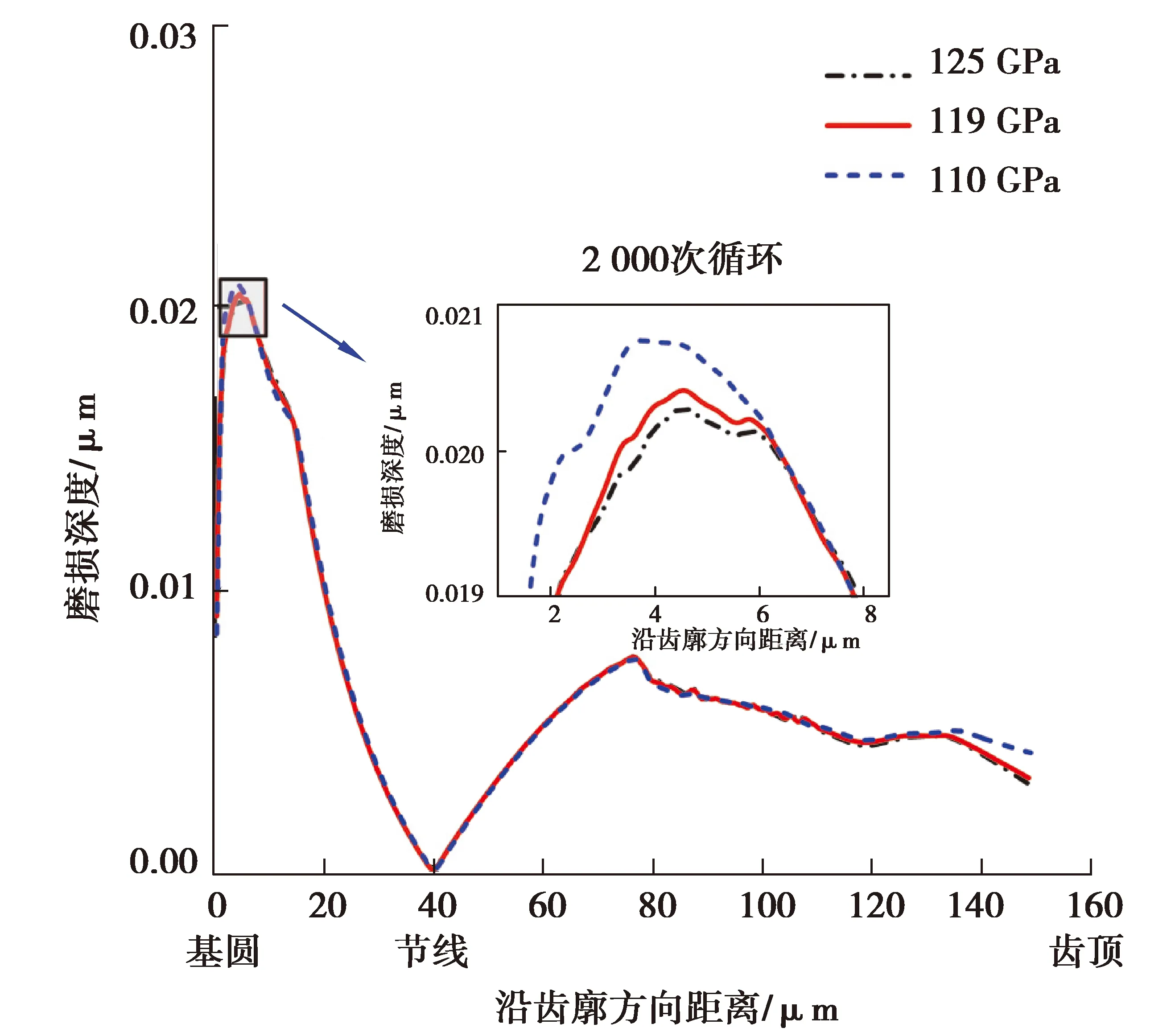
图12 不同弹性模量下从动轮磨损分布 Fig. 12 Wear distribution of driven gear under different elastic modulus
2.3.2 不同材料配对下齿面磨损分布及大小

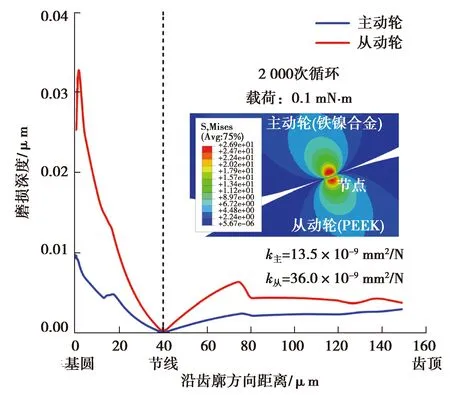
图13 金属-PEEK配对齿面磨损分布Fig. 13 Wear distribution of metal-PEEK paired tooth surface
3 结 论
针对微齿轮磨损失效问题,考虑主、从齿面的相互磨损作用,利用ALE自适应网格技术,编写了UMESHMOTION子程序,建立了微齿轮自适应磨损有限元模型。研究了微齿轮的磨损分布规律分析了材料性能及材料配对方式对磨损分布及大小的影响,并通过试验进行了相关验证,得到的结论如下:
1)研究发现微齿轮齿面磨损最严重的地方出现在靠近齿根的基圆附近,节线靠近齿顶次之,节线区域磨损几乎可忽略,与试验结果吻合良好。同时,最大磨损深度并非随着循环次数的增加而线性增加,其斜率(磨损速率)随着磨损循环次数的增加而缓慢降低。
2)铁镍合金微齿轮齿面在齿根附近及齿顶附近磨损形式存在差异,齿根附近表现出黏着磨损及磨粒磨损,齿顶附近表现为磨粒磨损。
3)选择较大弹性模量的铁镍合金材料对降低微齿轮磨损程度并没有显著影响,考虑铁镍合金材料与PEEK材料配对情况下,PEEK微齿轮磨损更为严重。
