基于直觉模糊熵权法的应急物资储备库选址评价模型
2022-04-22陈孝国CHENXiaoguo肖修鸿XIAOXiuhong杨悦YANGYue裴世博PEIShibo朱伟芬ZHUWeifen
陈孝国CHEN Xiao-guo;肖修鸿XIAO Xiu-hong;杨悦YANG Yue;裴世博PEI Shi-bo;朱伟芬ZHU Wei-fen
(①三明学院信息工程学院,三明 365004;②三明学院建筑工程学院,三明 365004;③东北大学信息科学与工程学院,沈阳 110819)
0 引言
进入新世纪以来,我国各种突发事件频频发生,从“非典”到“新冠”,从2008 年冰冻雨雪灾害到“5·12”汶川特大地震。自然灾害、事故灾害、社会安全以及各类突发事件影响着人们的正常生活和社会稳定。仅2014 年我国突发环境事件发生471 次,其中重大环境事件3 次,较大环境事件16 次,一般环境事件452 次。近50 年来,我国每年由各种自然灾害造成的直接经济损失约占国民生产总值的4%。面对频发的突发事件,人民群众对公共安全需求日益增长,突发事件应急体系建设面临更高的要求[1-3]。为保障公共安全和经济发展,应对突发事件过程中所需要的各类物资,如何合理确定应急物资储备库地址是成功应对突发事件的重要前提和基本保障,在救援中发挥着极其重要的作用。刘晋等[4]提出基于自适应遗传算法的应急物资储备库选址模型。郭换换等[5]利用区间规划模型对化工园区应急设施选址进行研究。张波等[6]采用统计分析的方法对应急物资分级储备进行研究。丛雯婧等[7]借助多目标优化方法构建了全局最优物资点选址模型。张聆晔等[8]构建了储备库选址评价指标体系并进行鲁棒性研究。上述成果从构建选址体系和决策方法上进行了广泛研究,但在指标取值及权重确定的合理性方面仍然不够完善,一是指标体系构建完成后指标权重往往直接给定或通过简单运算获得,误差较大且主观性强;二是指标取值随意性大,由于储备库选址相关指标参数取值无法精确获得,同时数据也是动态变化的,因此直接选用实数值不够合理。本文首先针对储备库选址的合理性构建了多层次指标评价体系,然后针对现有的储备库相关数据采用熵权法确定各指标权重,最后以福建省的物资储备库选址为例进行研究。
1 应急物资储备库选址评价模型
1.1 指标体系构建
V3={v31,v32,v33} 应急物资储备库地址的合理确定是顺利开展应急救援的关键环节[9,10]。本文在综合考虑已有成果的基础上,以交通条件、社会环境、公共设施、经济因素、自然因素为一级指标,以进出路线数量、通路质量、人口密度、区域覆盖率、干线通路数量、供水条件、供电条件、通讯条件、建设成本、管理费用、采购价格、地质条件、水文条件、地形条件为二级指标建立评价体系。
应急物资储备库选址指标体系V={V1,V2,V3,V4,V5},V1={v11,v12,v13},V2={v21,v22,v23},V3={v31,v32,v33},V4={v41,v42,v43},V5={v51,v52,v53},其中:V1—交通条件;V2—社会环境;V3—公共设施;V4—经济因素;V5—自然因素。v11—进出路线数量;v12—通路质量;v13—规划管理处。v21—人口密度;v22—地区经济实力;v23—区域覆盖率。v31—供电条件;v32—供水条件;v33—通讯条件。v41—建设成本;v42—管理费用;v43—采购价格。v51—地质条件;v52—水文条件;v53—地形条件。
1.2 直觉模糊集
定义1 设U 为论域,则该论域上的一个直觉模糊集A 为
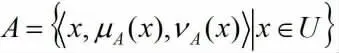
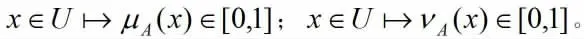
μA和νA分别表示A 的隶属函数和非隶属函数,且满足
πA是x 对A 的犹豫程度的一种测度。显然,对于任意
定义2 设U 为论域,A 和B 是U 上的两个直觉模糊集,实数λ>0,则
④交运算:
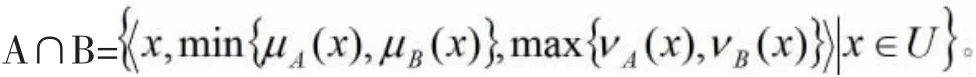
⑤并运算:
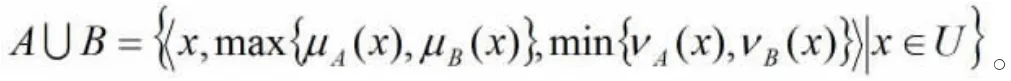
⑥和运算:
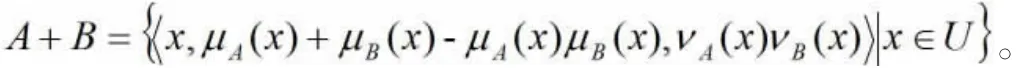
⑦积运算:
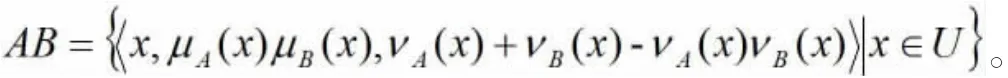
⑧与数的积运算:

⑨乘方运算:
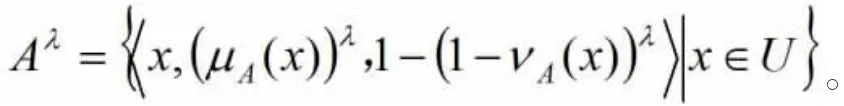
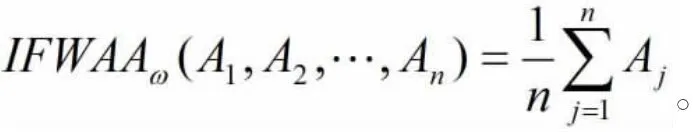
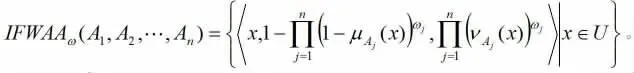
1.3 熵权法确定权重
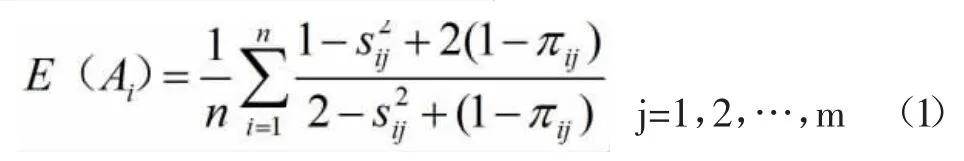
按照熵大权小的原则确定权重

1.4 TOPSIS 法直觉模糊综合评价
利用基于得分函数的方法进行排序,本质是将直觉模糊数的排序转化为实数,这样会丢失指标值的大量信息,从而造成排序结果不合理。TOPSIS 方法选择的方案不仅能保证既接近正理想方案,同时又远离负理想方案。
正理想解A+和负理想A-分别如下:
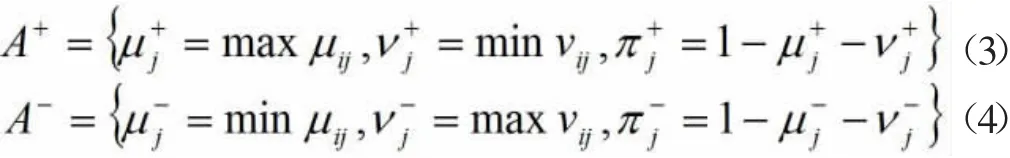
设因素指标Uij对应权重为,按照直觉模糊集理论可得Ai和A+的综合赋权距离公式为:
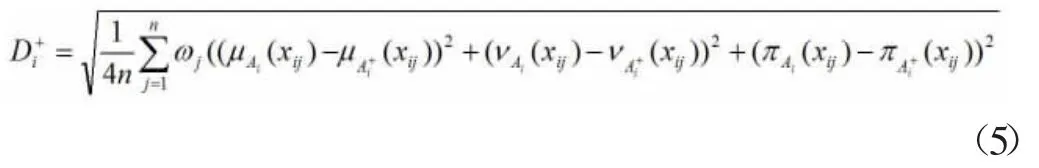
Ai和A-的综合赋权距离公式为:
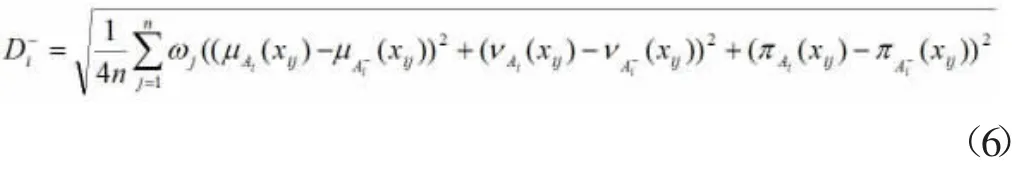
综合决策指数值。根据式(5)和式(6),确定各储备库选址地点的综合决策指数值,并按大小择优排序。
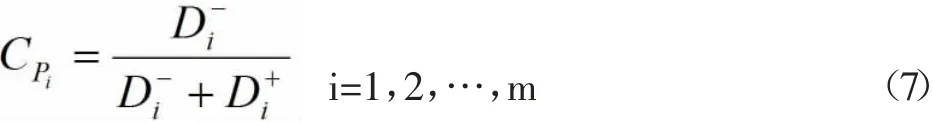
2 实例分析
福建省坐落在东南沿海一带,地方经济活跃,是海西经济区主要构成部分。特殊地理位置使其具备了较快发展优势,但同时地处沿海也使福建成为自然灾害较为严重的省份之一,风、洪、暴潮、涝灾害时有发生。自然灾害近些年制约着福建经济的快速发展,自然灾害很难消除,如何在灾害发生前做好应急物资储备、调度和发放,对缩短物资运输响应时间、合理分配、提高效率降低死伤率意义重大。通过专家对福建省福州、三明、南平、宁德、泉州的市级储备库选址各项指进行分析,得到直觉模糊评价值汇总表如表1。
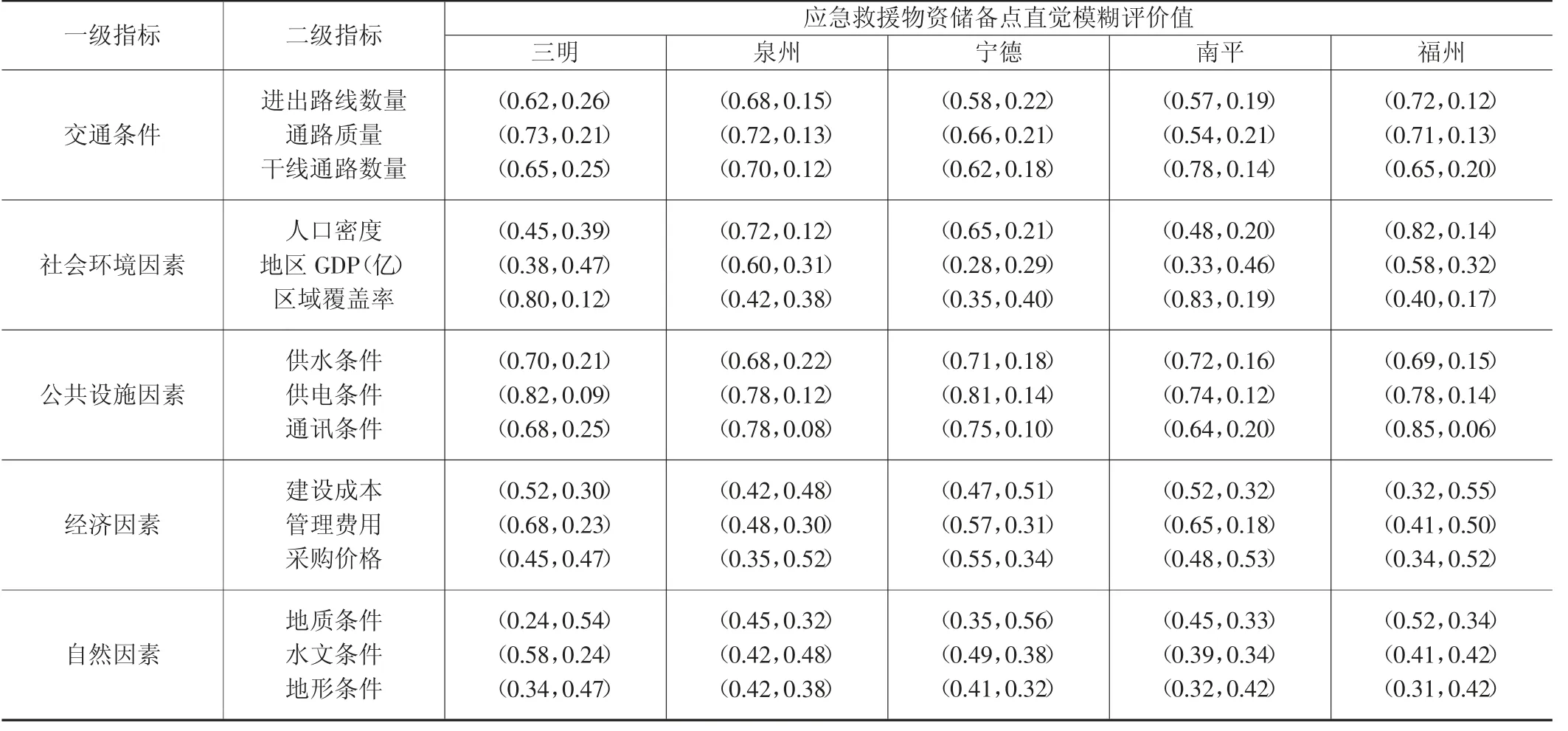
表1 应急救援物资储备点直觉模糊评价值
利用熵权法计算得到各指标权重如下:一级指标权重ω1=(0.2038,0.1917,0.2362,0.1976,0.1708);二级指标权重ω2=(0.3155,0.3395,0.3449;0.3532,0.3020,0.3448;0.3103,0.3582,0.3315;0.3279,0.3305,0.3416;0.3448,0.3484,0.3068);总 权 重ω=(0.0643,0.0692,0.0703;0.0677,0.579,0.0661;0.0733,0.0846,0.078;0.0648,0.0653,0.0675;0.0589,0.0595,0.0524)。按照公式(7)计算得到福建省各个相关地级市综合评价指数值,见表2。

表2 计算所得各地级市的市级应急救援物资储备点选址得分值
3 结语
灾害应急救援物资储备库选址影响因素较为复杂,本文以交通条件、社会环境和公共设施等5 个因素为一级指标,以进出路线数量、通路质量和干线通路数量等15 个因素为二级指标构建评价指标体系,相对全面合理。将全部指标对应的直觉模糊数进行熵权法确权后,借助TOPSIS法确定正负理想解,通过综合评价指数值得到关于宁德的应急物资储备点选址较低于其它地级市的选址得分,泉州作为待选储备点得分值最高。
