画数学，思维的“拐杖”

许玲娜

[摘要]数学是一门思维容量较高的学科，它具有高度的概括性，而小学生尤其是低年级学生的思维是以直观形象思维为主，如何平衡两者之间的关系，“画数学”不失为一个好办法。“画”让每一个孩子的思考变得与众不同，“画”让每一个孩子的思考跃然纸上。

[关键词]画数学;思维;直观形象

在关注学科核心素养的当下，“用数学的语言表达现实世界”已成为基本共识。如果说，语言是思维的物质外壳和边界，那么画就是小学生学习数学的思维外衣。画能够让学生把自己的数学思维外显出来。画数学，也就给学生的数学思维穿上了一件“华丽”的外衣。

《义务教育数学课程标准（2011年版）》把几何直观作为十大核心概念之一，提倡利用图形描述和分析问题，并指出：在日常教学中，指导学生学习的过程中，帮助学生养成画图的习惯至关重要。因此在教学中，教师应引导学生借助示意图或线段图，在直观理解的基础上解决问题。

一、“画”出需要——有需要才画

所谓“画数学”，是指学生在学习数学的过程中，用简单的图形表示出题目的意思，或者用“画画”的方法表达自己的思维过程的一种学习方法。从本质上看，“画”是帮助学生解决问题的思维工具，而工具的价值在于能否满足学生的实际需要，因此，“画数学”是出于学生本身解决问题的需要。

（一）百思不解，寻求“突破”

小学生的思维是灵活敏捷、富有创造性的，却又受定性思维的影响。数学问题有时也会“调皮”地跟孩子们玩迷宫战术，让学生束手无策，使学生在自主探索中常常无法选择对的方法和策略，从而出现思维受阻的情况，这时候就需要另辟蹊径，寻找新的突破点。由于小学生的思维以直观思维和形象思维为主，这时候“画数学”就起到了一种“桥梁”的作用，通过“画数学”，可以将较为死板的文字或符号转变成生动鲜明的图形，将抽象的数学直观化、形象化、具体化，使学生在画的过程中更好地丰富数学感知体验，发展思维能力，走出思维迷宫，清晰数学思路。

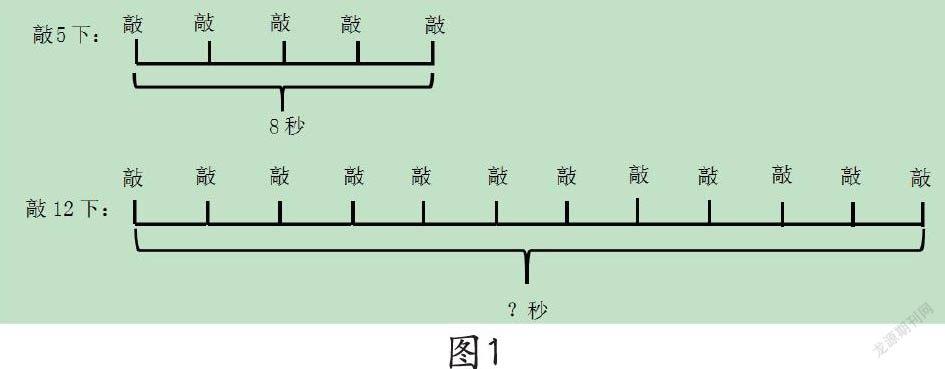
例1：敲钟问题“广场上的大钟5时敲5下，8秒钟敲完。12时敲响12下，敲完需要多长时间？”对于这种典型问题，学生刚接触时束手无策，分不清谁代表棵树，谁代表间隔数。此时我引导学生试着画一画，把抽象的文字描述变成直观的图形表征。学生边画边讨论，很快就有学生举起手，此时我没有着急让他们回答，而是让学生们先在小组内交流画的过程，再小组汇报。学生汇报时，对自己画出来的图（如图1）进行解释说明：“大钟敲5下有4个间隔，每个间隔2秒，12时敲响12下，中间有11个间隔，所用时间是11x2=22（秒）”。这样一来，“看不见”变为“看得见”，学生一目了然。

（二）心存疑虑，直观“验证”

苏霍姆林斯基曾说过：“图画是发展创造性思维和想象力的手段之一，是通往逻辑认识的道路上必不可少的阶梯。如果哪个孩子学会‘画应用题，可以有根据地说，他一定能学会解应用题。”儿童的智慧在他的手指间，给学生一张草稿纸，把数学画出来，使抽象的问题直观化，数量关系明确了，问题也就迎刃而解，这也是用“画数学”进行直观验证的好处。

例2：解决问题“在一个正方形花园的四周种树，每边种5棵，至少要多少棵树？”很多学生这样算：4x5=20（棵）。老师问“真的有20棵？”“只有16棵。”有个学生说到，“我通过画图，发现正方体的四个角上都有一棵树被数了两次，所以还要从20棵里面再减去4棵。”听他这么一说，孩子们纷纷动手画了起来（如图2），结果一数，真的只有16棵树！”

二、“画”出价值——让思维的轨迹更清晰

我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微;数形结合百般好，隔离分家万事休。”作为教师，在教学过程中，应重视数形结合思想方法的熏陶，注重“画图策略”的培养，《数学课程标准》也指出：“通过义务教育阶段的数学学习，要使学生能了解数学的价值。”因此，让学生“画数学”，不是“画”了就会产生价值，在教学的过程中，教师的主动参与和积极引导才是学生“了解数学的价值”的前提。

例3：教师教学《植树问题——两端都种》时，可以这样引导：

第一层次：动手操作，初步体验

题目：在20m的沥青路一边植树，每隔5m栽一棵（两端要栽）。需要准备多少棵树苗？教师引导学生用学具摆一摆，并示范每一个5米就摆一棵树（如图3）      ， 使学生初步感知棵数比间隔数多1。

第二层次：数形结合，深入体验

题目：在全长25m的沥青路一边植树，每隔5m栽一棵（两端要栽），一共要栽几棵树？此时，教师引导学生用画线段图的方法画出来，使抽象的数学具体化。（如图4）

第三层次：合理推测，感知规律

如果这条沥青路长30米、35米……又应栽几棵树呢？

教师让学生在不断的操作和交流中，充分体验和感悟，经历摆一摆、画一画的全过程，使学生明确“间隔数”与“棵数”这两者之间“一一对应”的关系，此时学生没有摆，没有画，却能纷纷举手直接回答，学到解决问题的方法。

画的最终目的是为了不画。通过设计三个层次的练习，层层递进，使学生从“摆一摆”“画一画”中得出规律：两端都种时，棵数=间隔数+1，通过数与形的结合，帮助学生建构数学模型，解决实际生活种的植树问题，学生在“画”中感悟到其作为策略的价值，使“画”有所值。

三、“画”出个性——给予“画”的自主权

陈鹤先生指出：“绘画是言语的先导，表达美感之良器。”每个孩子都会有绘画的天性及自己的理解，因此教师在教学过程中应给予学生“画”的自主权，让学生从本身已有的知识经验出发，才能彰显个性，碰撞出思维的火花。

例4：在学习分数乘除法，学生很容易混淆“单位1”，此时可以通过题组，让学生分析题组中每道题的异同，根据自己的理解通过画图来表达问题中的数量关系。（如图5）

学生通过画，凸显了每道题的异同之处，学生说不清思维数量关系，通过画也变得更加清晰具体了。

例5：教完《简易方程》这个单元时，我让学生用思维导图梳理本单元的知识点，学生交上来的作品放飞了学生的思维，释放了学生的激情，如图6。

例6：在2020年“加长版”的寒假里，我们采用了刘燕老师推出的“像数学家一样探究”系列课程对孩子们进行“充电”，在即将复课时，我让学生用自己喜欢的方式记录自己的收获与体会、困惑和难题，学生交上来的作品既让我为他们的脑洞大开、创意十足感到惊喜，又为他们的一丝不苟、认真细致所感动，如图7。

画，放飞了学生的思维;画，释放了学生的激情;画，引领着学生走进五彩缤纷的数学王国。在数学学习过程中，我们可以因势利导，在“画数学”中感悟数学思想，让每一个孩子的思维得到放飞;在“画数学”中培养创造力，让每一个孩子的思考变得与众不同;在“畫数学”中感受数学知识的奥秘，感受数学学习的乐趣，让“画数学”成为学生思维的“拐杖”。

参考文献

[1]刘善娜.把数学画出来—小学画数学教学实践手册[M].北京：教育科学出版社，2019-09.

[2]中华人民共和国教育部.义务教育数学课程标准（2011版）[S].北京：北京师范大学出版社，2012-01.

[3]孙蕾.“画一画”，数学更精彩[J].读写算（教育导刊），2013（24）.

[4]周雪.经历探究过程 渗透数学思想方法——《植树问题》（两端都栽）案例设计与反思[J].湖北教育（教育教学），2018（03）：58-59.

[5]杨传杰.浅析数学教学中的“画数学”[J]，新教育时代电子杂志（教师版），2015-08.