基于面板数据供应链弹性评估——以制造业为例

1 研究背景

制造业一直是我国重要的经济支柱。改革开放后，我国工业实现了跨越式发展，产业范围迅速扩大，整体实力稳步提升。我国已成为世界上门类齐全、规模较大的制造业国家。不可置否的是，隐藏在“中国增长奇迹”背后的重要驱动力正是来源于以制造业为核心的工业体系。然而，2019年底爆发的新冠疫情影响了诸多制造行业的发展，对生产制造中的供给端、需求端与供应链造成显著影响，引起制造行业的“适度恐慌”[1]。

因此，企业应对中断、干扰事件的能力不仅是必要的，还是一种非常有价值的战略竞争优势。在这种背景下，制造行业需要构建一种应对中断、干扰事件的风险规避或快速恢复能力的新型供应链，即弹性供应链，以支持企业的可持续发展。

续 表

2 研究现状

国内学者对供应链弹性的研究相对较晚。赵林度认为供应链弹性是供应链适应性和自我实现能力，会影响整个供应链的基本效益与竞争力[2]。王宇奇等认为供应链弹性应具备以下特征：一是面对特定环境，只有受到突发事件的冲击，供应链受到扰动时，弹性才能够发挥作用；二是反应能力[3]，即面对扰动供应链能够感知并迅速做出回应的能力。如今，越来越多在弹性供应链设计领域的论文不断发表，该主题已被学术界公认为热门和新兴的研究领域。

3 弹性评价指标体系及模型构建

基于以上背景，本文构建了表1所示的评估制造业供应链弹性的指标体系。

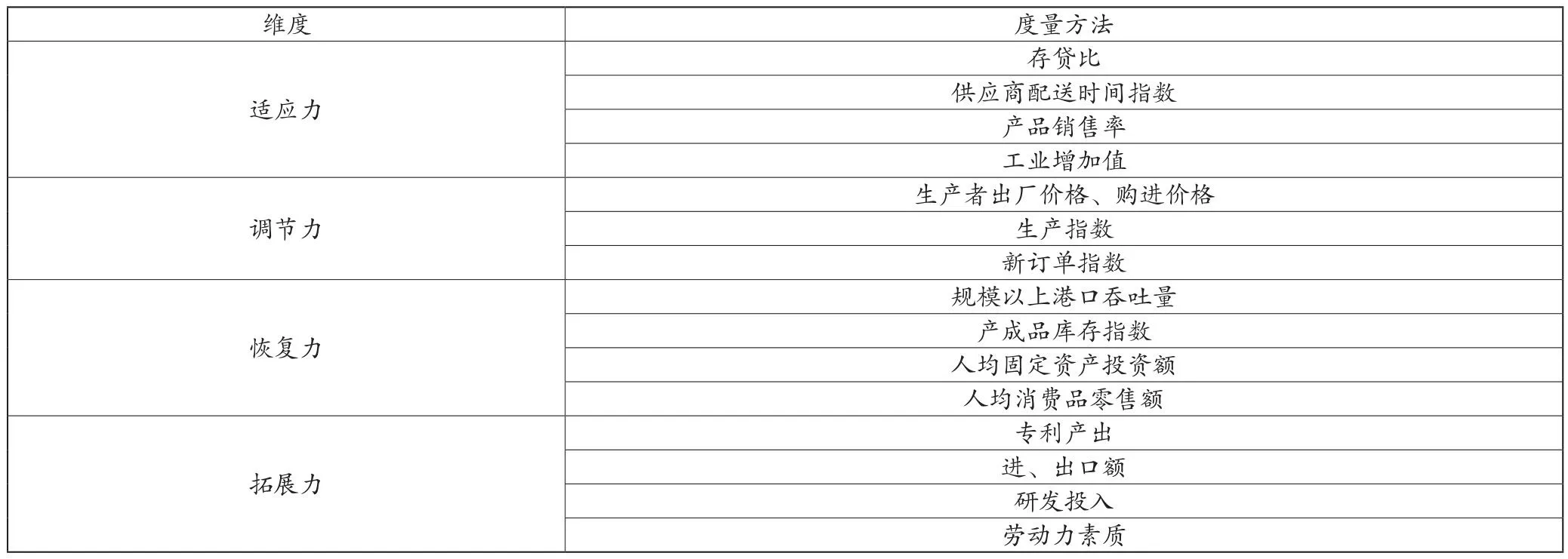
表1 制造业供应链弹性评价指标体系

数据来源于《中国工业经济统计年鉴》及国家统计局官网。因子分析法用于分析年度横截面数据，以获得各省的综合得分和因子得分，利用Topsis综合评价法计算各省份的总因子得分和理想解的接近度，评估各省供应链的弹性水平[4]。

3.1 建立指标体系

设研究对象为Pti（i=1，2，...，n），指标为Xij（j=1，2，...，m）其中t∈[t1，t2]为评价对象的个数，若评价区间为L年[5]，则t2-t1=L。

3.2 因素分析评估

首先，对指标进行进一步处理和标准化，并对断面数据进行因子分析，得到对象集Pti每年的综合因子得分，形成综合因子得分矩阵（Yti）n×L（i=1，2，...，n），其中i为研究对象，t∈[t1，t2]为评价对象的个数。评价对象集Pti（i=1，2，...，n）的综合因子得分为Yti。设置指标体系的年度因子得分，即L个变量、n个研究对象，然后对其进行归一化处理，Qti=Yti/ Σnt=1Yti2，其中i为研究对象，t∈[t1，t2]为年份，Yti是综合因子得分，Qti是归一化处理后的综合因子得分[6]。

设t1-t2年Qti的最大值为最优向量Q+，Qti的最小值为最劣向量Q-，Q+=（Qmax，1，Qmax，2...，Qmax，L），Q-=（Qmin，1，Qmin，2...，Qmin，L），

设第i个评价对象Qti与最优解的接近程度为

设第i个评价对象Qti与最劣解的接近程度为

设第i个评价对象Qti的最优解贴进度为Ci，则如果C越大则说明该对象制造业供应链弹性越好。i

4 因子分析

本文借助Matlab软件对我国各地区的制造业供应链弹性评估指标体系的截面数据分别进行因子分析。

4.1 数据KMO检验和Bartlett检验

在使用因子分析之前，需要进行KMO检验，检测变量间的偏相关系数，本文的检验结果如表2所示，说明因子分析是可行的。

4.2 截面数据公共因子的提取及综合得分的计算

表3显示了样本数据的结果，使用因子分析获得了特征值大于1的前4个因子数据，即因子累积方差的百分比大于80%，说明通过该方法提取的前4个因子可以解释制造业供应链的弹性水平，而其他因子可以忽略不计。

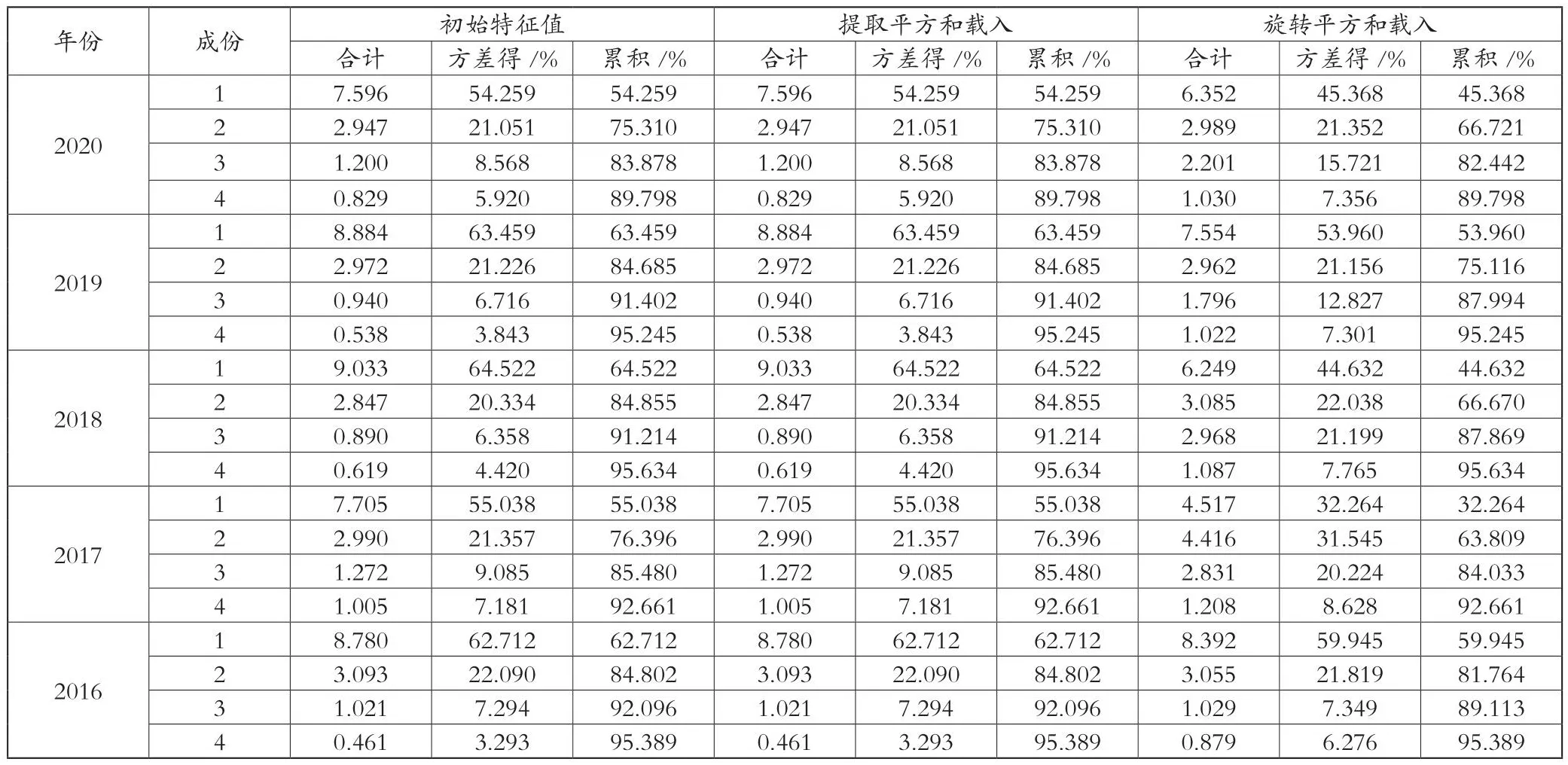
表3 累计方差值

本文对因子载荷矩阵进行方差最大化旋转。虽然每个指数的具体因子载荷量每年都有所不同，但是对公因子的具体解释不受不同载荷量的影响。

本文仅对2020年数据进行解释。从表4可以看出，计算得出的第一个公因子在产成品库存指数、生产指数、购进价格指数上具有较大的载荷，可以定义为生产水平因子；第二个公因子在人均固定资产投资额、进出口额、研发投入上具有较大的载荷，可以定义为融资水平因子；第三个公因子在规模以上港口吞吐量、供应商配送时间指数上具有较大的载荷，可以定义为物流水平因子；第四个公因子在劳动力素质、存贷比上具有较大的载荷，可以定义为冗余资源水平因子[7]。

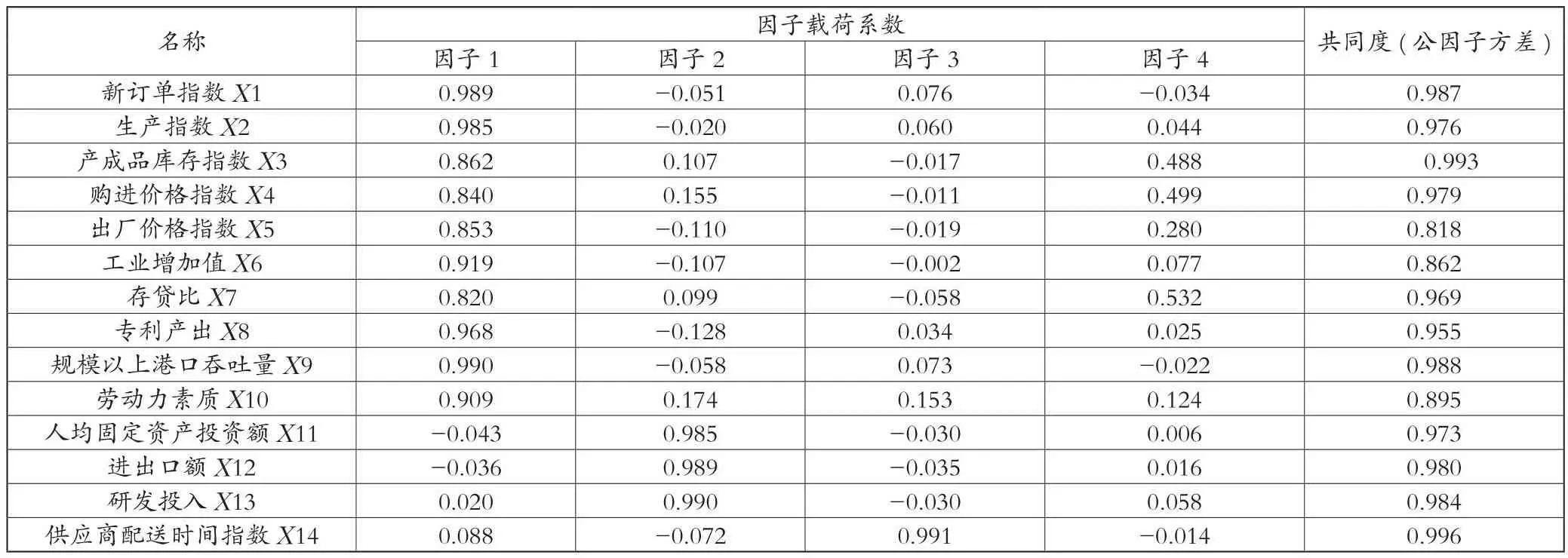
表4 旋转后因子载荷系数表

表5的结果显示，2016—2020年31个省（自治区、直辖市）的最高和最低分数之间存在较大差异， 24个省份的得分为负，这表明制造业整体供应链的弹性较低，各地区的差异性明显，表现为东部发达省份处于领先地位，而西部经济薄弱地区较为落后。落后地区的总体因素得分较低，表明这些地区应重点发展本地供应链的基础设施，以促进该地区整个供应链的发展，而发达地区的因子得分较高，表明制造业供应链弹性水平的高低与当地的经济发展水平息息相关，制造业的发展需要完善的金融市场支撑。同时从表5中可以看出，2016—2020年，31个省（自治区、直辖市）每年供应链的弹性结果不同，采样期间的结果排名也不同。这是因为截面数据是独立的，所以不可能简单相加得出总年度综合因子得分，否则会影响数据的客观性。因此，根据上述因素分析的结果，本文采用Topsis综合评价方法，以弥补无法在面板数据中进行因子分析加和以反映供应链弹性水平的缺陷。

表5 制造业供应链弹性水平综合因子得分

5 基于因子分析法的Topsis综合评价法

基于前文Topsis方法的描述，可以得到2016—2020年各省供应链弹性水平的总体评估和排名结果。如表6所示，可以看出，我国城市化水平相对较高的地区Ci+相对较高，相关评估结果领先，经济水平较差的地区供应链弹性也较差。结论与因子分析法的结果相似。该结果反映了整个样本数据期内各地区供应链弹性的总体排名。

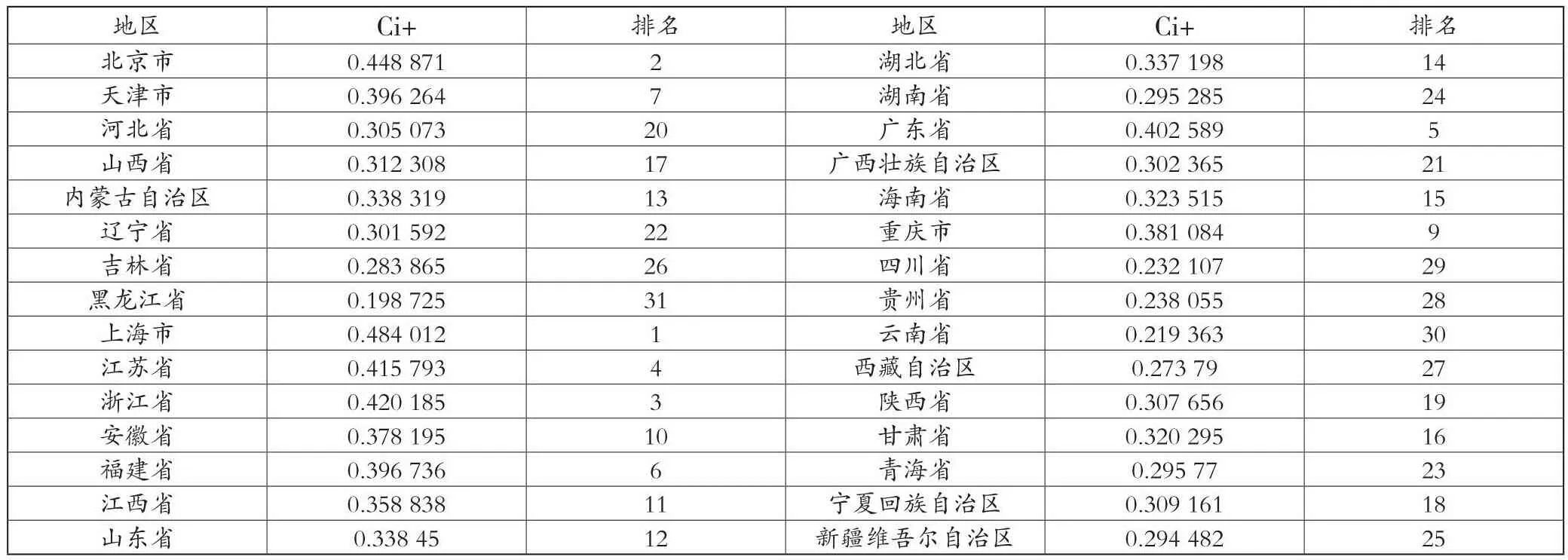
表6 各地区供应链弹性的总体排名

6 结论及建议

本文以制造业供应链弹性为研究对象，运用基于Topsis 改进的因子分析模型对其弹性进行综合评价；研究发现，2016—2020年，制造业的弹性水平每年的最高和最低结果之间存在较大差异，而且最优解贴近度最大值与最小值存在较大差距，我国31个省份制造业供应链弹性综合因子得分与最优解贴近度分布在0.2～0.5，且没有省份超过0.5，这说明供应链弹性的地区异质性是显著存在的，且行业的弹性水平有待加强。

为了构建弹性供应链。应当坚持市场调节和政府引导相结合，增加对工业发展的政策支持，重视企业的科技创新，促进传统工业向高新技术制造业的转变，优化制造业的产业结构。同时，需要选择适当的财务方法，科学使用融资杠杆，鼓励中小企业利用数字普惠金融解决融资难题，走科技含量高、经济效益好、资源消耗低的道路。