基于SARIMA时间序列模型的区域快递需求预测——以江苏省为例

0 引 言

随着经济的高速发展，人们的消费需求不断升级，快递业也日益发展壮大。根据《中国快递业社会贡献报告2021》的报道，我国快递业已经连续8年稳居世界前列，全年快递业务量和业务收入达到1 083亿件和10 332.3亿元，快递业已经成为拉动国民经济发展的重要力量。

江苏位于长江三角洲地区，是我国综合发展水平最高的省份，省域经济综合竞争力居全国前列，人均GDP自2009年起连续13年全国领先，是我国经济最活跃的省份之一。作为我国经济强省，江苏省的快递业务量位居全国第三，十年内增长了13倍。截止到2022年11月，江苏省邮政快递业务量累计78.8亿件，同比增长3.4%，快递业务收入累计740.7亿元，同比增长1.1%。可以说，快递业务已经成为江苏经济发展的重要领域之一。但是，经济下行使得我国各省市经济和居民生活受到影响，许多居民从线下购物转为线上购物。这些不确定因素给快递行业带来了更大风险，除了季节性因素带来的周期性快递业务量波动之外，快递业务量数据出现暴跌和骤增都暴露了我国在快递行业还存在许多问题[1]。区域快递量预测不仅能为快递行业提供更多的数据支持，还能相应地提高快递行业对风险的事前预测和事后评估能力，更好地助力物流和快递行业的发展[2]。SARIMA模型在金融、交通、医学、电力等领域都有广泛应用，是统计模型中常见的时间序列预测模型。由于快递量时间序列数据存在明显的季节性特征，故本文采用SARIMA模型。

1 SARIMA模型和建模步骤

1.1 统计方法与工具

Python是一门免费开源、简单、高效的面向对象的编程语言。Anaconda为Python发行版本，其中包含180个科学包及其依赖项。本文将采用其中的Numpy，pandas，matplotlib，Scikit-learn，statsmodels，pmdarima等Python库进行数据分析及可视化、统计分析、模型建模等[3]。

同时，在人工智能、大数据分析等技术飞速发展的环境下，智能化的信息搜索和收集方式更受人们欢迎。网络爬虫技术可以模拟人类的上网行为，在互联网上“爬取”信息，并且对网页信息进行提取，自动保存。本文采用了爬虫技术，完成了数据的采集、处理、储存[4]。

1.2 SARIMA时间序列模型

季节性差分自回归滑动平均模型(Seasonal Autoregressive Integrated Moving Average，简称SARIMA)，是常用的时间序列预测模型，其在自回归移动平均模型（Autoregressive Integrated Moving Average，简称ARIMA）的基础上考虑了季节性因素。SARIMA模型在金融、交通、医学、电力等领域都有广泛的运用。由于快递业存在明显的季节性特征，故本文采用SARIMA模型。

1.3 SARIMA模型的建立步骤

1.3.1 数据处理

在获取到原始时间序列之后，通过Python的pandas库导入数据，并将原始数据拆分为测试集和训练集。使用训练集完成对模型的训练，将测试集作为模型测试的数据，评估模型的准确性。

1.3.2 数据检验

在分析时间序列数据之前，需要对相关原始数据进行检验。首先，要判断时间序列数据是否具有平稳性，即通过ADF单位根检验，若数据是稳定的，那么可以直接使用SARIMA模型进行建模分析，否则需要进行d阶差分和D阶差分处理，直到数据通过平稳性检验。

1.3.3 白噪声检验

白噪声检验，即判断经过处理的稳定时间序列数据是否是随机序列，因为随机序列不具有分析意义。图1为SARIMA模型建立过程。

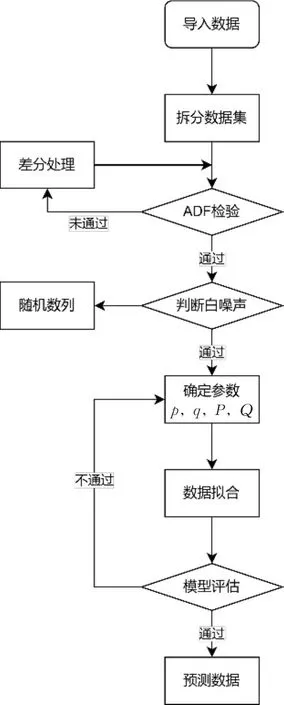
图1 SARIMA模型建立过程

1.3.4 确定参数

确定时间序列数据是稳定、非随机的，那么要对SARIMA（p，d，q）（P，D，Q）m模型参数进行选择，即通过自相关分析和偏自相关分析的大小来分析时间序列是否拖尾，确定趋势自回归阶数p、趋势移动平均阶数q、季节性自回归阶数P、季节性移动平均阶数Q；也可通过遍历AIC（最小化信息量准则）和BIC（贝叶斯信息准则）的方式找到最佳参数。

1.3.5 判断检验

确定模型的残差序列是否为白噪声，即是否属于随机序列，若是则检验通过，说明原始时间序列中的信息已经被提取，不用再进一步分析了，否则需要重新进行参数的调整和确定。此外，还要观察残差图是否符合正态分布[5]。

1.3.6 预测及评价

将测试集和SARIMA（p，d，q）（P，D，Q）m模型的预测数据进行比对，若误差较小，则说明模型可行，否则说明模型的误差较大，预测的性能较差。若预测误差小，则使用该模型对未来数据进行预测。

2 模型分析与预测

由图2可知，江苏省快递量呈逐渐上升趋势。

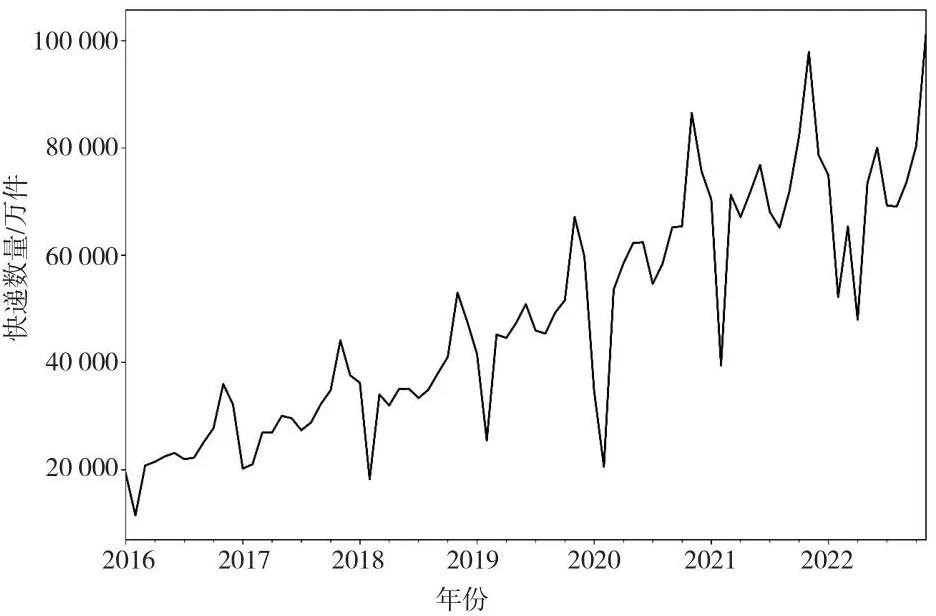
图2 江苏省2016年1月—2022年11月快递业务量

将原始数据进行分解，得到趋势图、季节性图和残差图（见图3）。结果显示，江苏省快递业务量的季节性明显。一年中的11月左右达到物流量的最高峰，2—3月份为物流量的最低谷。其主要原因为：由于春节导致快递停运使物流量下降；每年的“双11”等线上促销活动使得物流量达到高峰。物流量趋势在2016年1月—2021年6月明显上升、2021年7月—2021年12月开始趋于平稳。其主要原因为：国内面临经济下行的困难局面，经济增长变缓；“双11”期间消费者的购物需求明显降低，商家担心库存积压、减少参与活动等。

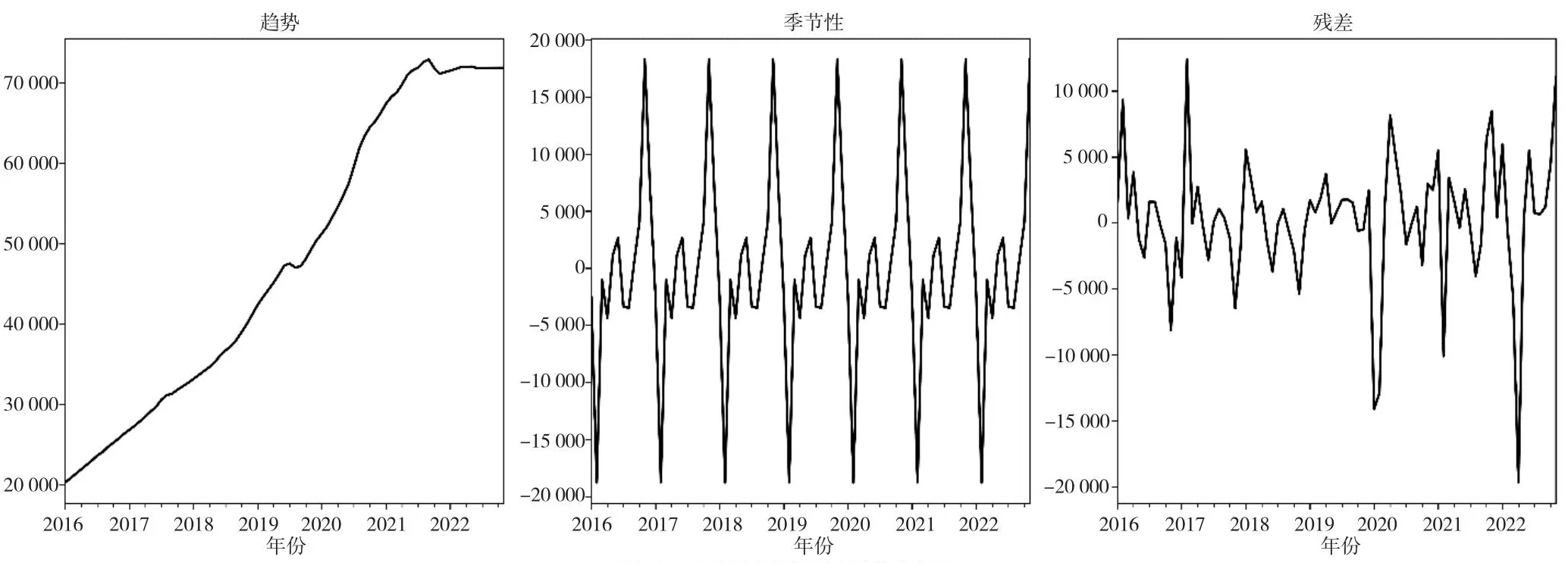
图3 原始时间序列分解图

2.1 划分训练集和测试集

将2016年1月—2021年6月的数据进行划分，2016年1月—2021年12月的前72个数据作为训练集，2022年1月—2022年12月的11个数据作为测试集。

2.2 时间序列的平稳化处理

Augmented Dickey-Fuller test(增项DF单位根检验，简称ADF)是时间序列分析中常用的检验方法，表1是对2016年1月—2021年12月江苏省快递业务量进行ADF检验的结果。对原始数据进行检验，p值大于0.05，说明原始数据是不平稳的。在经过一阶差分处理后，p值小于0.05且t值小于显著性水平，说明一阶差分后的数据是平稳的。从原始数据分解图（见图3）可知，原始数据存在明显的季节性，其周期为12，对一阶差分后的数据进行季节性差分，p值小于0.05，且t值小于显著性水平，说明在一阶差分和季节性差分之后得到了平稳序列，可以进行下一步分析。同时，从表中可以得知差分阶层d、季节性差分阶层D均为1。根据上述分析，可以确定模型为SARIMA（p，1，q）（P，1，Q）12。

表1 对2016年1月—2021年12月江苏省快递业务量进行ADF检验的结果

2.3 白噪声测试

Ljung-Box检验，用来检验m阶滞后范围内序列是否为随机序列[6]；在statsmodels库中可以使用acorr_ljungbox函数进行分析。差分后的时间序列经检验，p＜0.001，为非白噪声即非随机序列，可以继续分析。

2.4 模型定阶

自相关阶数p、滑动平均阶数q和季节性参数P、Q可以根据ACF图（自相关图）、PACF图（偏自相关图）来确定，也可以通过遍历AIC（最小化信息量准则）和BIC（贝叶斯信息准则）最小参数组合来确定。从图4可以看出，原序列在经过一阶差分和季节性差分之后得到了平稳序列，可以开始进行模型的建立。通过网格搜索得到模型的最佳参数为SARIMA（1，1，1）（0，1，2）12。经过白噪声测试，模型的残差为随机序列，说明信息已经被提取。

图4 自相关系数图和偏自相关系数图

2.5 模型估计

从表2中可以得知采用SARIMA（1，1，1）（0，1，2）12模型对2022年1月—2022年11月的数据进行预测，相对误差的范围在-0.22%～0.71%，结果显示模型的预测效果良好。图5为SARIMA（1，1，1）（0，1，2）12模型测试集的拟合。

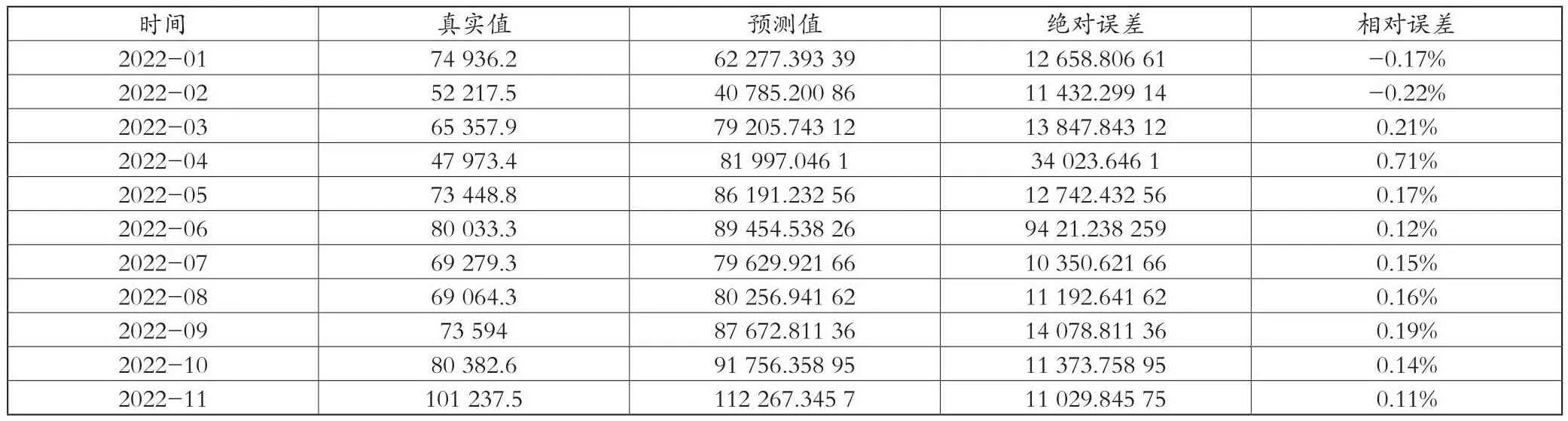
表2 测试集真实数据和预测数据的比较

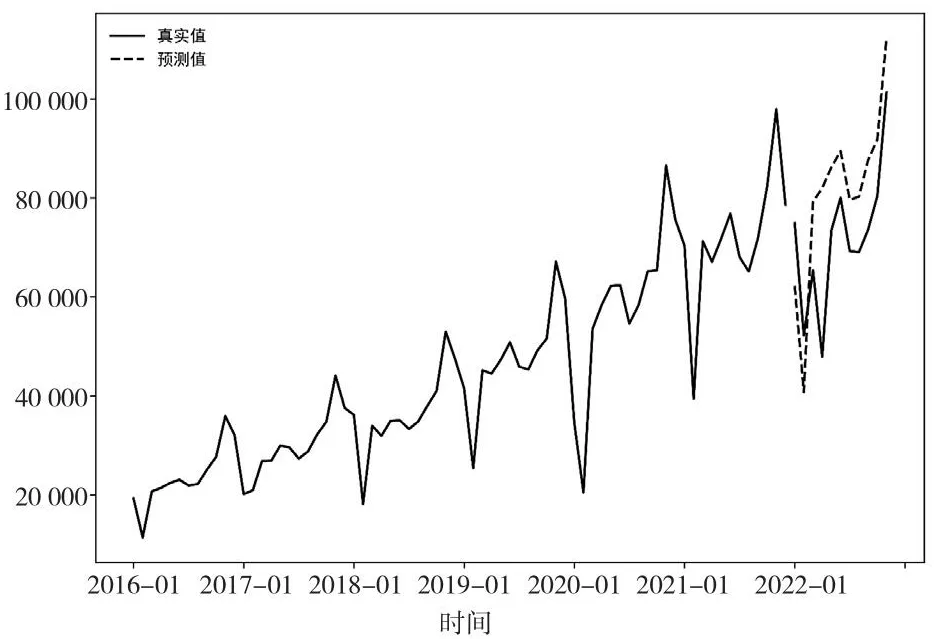
图5 测试集SARIMA (1, 1, 1)(0, 1, 2)12的拟合图

2.6 预测数据

SARIMA模型对于短期时间内的预测是比较准确的，随着预测时间的延长，误差便越来越大。所以选择未来半年的数据预测未来目标。在模型评估后对2022年12月—2023年5月的江苏省快递业务量数据进行预测，见表3。

表3 江苏省2022年12月—2023年5月快递量预测

3 结 语

通过对2016—2022年的快递业务量进行分析，结果表明，SARIMA模型在短期时间内的预测效果较好，可以将预测数据作为未来短期物流需求量的参考指标。虽然由于经济下行等原因造成快递量的波动和近期快递需求量变缓，但从长期来看，这些因素对快递行业的影响会逐渐减小。从原始快递量数据的季节、趋势分离结果来看，每年11月是快递业务量的高峰期，快递行业会面临一年中最大的机会和挑战，在保证物品配送、运输、搬运效率的同时，也要确保安全性，提升服务质量。对于商家来说，应提前制订好库存计划、配置好资源、人员等，以面对可能出现的风险和机遇。在“双11”“双12”等线上促销活动中应当抢抓商机，制订更加合理的营销方案；对于电商平台来说，要为消费者和商家建立合理的购物平台，提高消费者的消费体验，保障消费者权益等；对于快递服务商来说，应该提高服务水平，确保商品运输的质量安全性，合理制订计划，避免库存积压等问题的出现。春节前后是快递量的低潮期，在面临可能需要减少资源投入时，物流和快递服务商应制定好相应的措施。在此过程中，区域快递量预测和需求预测是必要的。

文章只考虑了包括季节性时间序列的单个因素，如果能够考虑多种因素的组合实现区域快递需求量预测将会使得该模型更加完善，影响快递业的因素有许多，例如宏观因素有区域经济、信息化程度、工业化程度、全球化程度、运输化程度等；微观因素有从业人员数量、基础设施等[6]，除此之外还要考虑一些突发情况。