一种基于三维可变换CNN加速结构的并行度优化搜索算法

屈心媛 徐 宇 黄志洪 蔡 刚 方 震

(中国科学院空天信息创新研究院 北京 100190)

(中国科学院大学电子电气与通信工程学院 北京 100049)

1 引言

卷积神经网络(Convolutional Neural Network,CNN)以其突出的性能优势，在人工智能领域引起了广泛的关注，并被应用于图像分类、人脸识别、自动驾驶和医学成像等场景中。LeCun等人[1]于1998年提出了第1个经典CNN模型LeNet-5。此后，随着人工智能的发展，CNN的结构变得越来越复杂—层数更深，规模更大，计算量迅速增加。这为CNN硬件加速器的设计带来了巨大的挑战。图形处理器(Graphic Processing Units, GPU)、专用集成电路(Application Specific Integrated Circuit,ASIC)、现场可编程门阵列(Field Programmable Gate Array, FPGA)是常见的CNN正向推断平台。其中，基于FPGA的CNN硬件加速器因高并行、低功耗、可重复编程的特性，越来越受到学界和业界的广泛关注。

CNN是一种计算密集型网络，合理利用FPGA片上计算资源是加速器设计的关键。然而，文献[2]经过客观全面的评估指出，许多现有CNN加速器的计算资源利用率不理想，这降低了加速器的计算吞吐率和性能功耗比[3–9]。卷积计算结构与并行度算法灵活度不足是限制资源利用率优化的主要原因，例如：文献[6,7]中卷积计算结构的时间粒度与资源粒度不均衡、文献[8]中并行度探索空间受限等。

为优化加速器性能，文献[2]提出了一种3维可变换的CNN加速结构，通过细粒度调节极大地提高了计算结构的灵活性。为选取与计算结构匹配的并行度配置方案，本文提出一种并行度搜索算法。该算法在取值区间内以最细粒度遍历可行的并行度组合方案，筛选出资源利用率最高的并行度方案。然而，结构灵活性的提升导致并行度探索空间爆炸增长，带来遍历元素过多、计算量过大的问题。这使得搜索最优并行度的时间开销激增，严重降低了加速器实现的可行性。为此本文提出一种优化搜索算法。该算法首先通过多轮迭代的数据筛选，高效地排除冗余的并行度方案，压缩了超过99%的搜索空间。之后算法采用剪枝操作删减无效的计算分支，成功地将计算所需时长从106h量级减少到10 s内。该算法适用于不同规格的FPGA芯片，其搜索得出的最优并行度配置方案性能突出，可在不同规格的芯片上实现平均(0.957, 0.962)的卓越的计算资源利用率。

本工作具有普适性，可被广泛应用于LeNet5,AlexNet, ResNet等经典CNN网络的加速工作中。其中AlexNet获得2012年ImageNet大规模视觉识别挑战赛冠军[10]，自此被广泛应用于图像识别领域。本文以AlexNet这一经典CNN网络作为验证模型，通过计算结构与并行度灵活配合，16 bit量化下在Xilinx KCU1500开发板实现了(0.955, 0.962)的计算资源利用率、2425.455 GOP/s的吞吐率、62.351 GOP/(s·W)的性能功耗比。本工作大幅提高了片上计算资源利用率，相比于其他FPGA CNN加速器[4,11,12]实现了吞吐率和性能功耗比的明显优化。

本文内容安排如下：第2节介绍CNN网络特性与AlexNet结构参数；第3节分析现有研究现状，提出加速器设计优化方向；第4节简述加速器硬件架构，并详细介绍一种细粒度迭代优化并行度搜索算法；第5节分析加速器性能参数，并与其他现有工作进行对比。

2 CNN算法分析

CNN是一种通过处理输入特征图数据以产生分类结果的网络，其由4个核心部分构成：卷积(CONVolution, CONV)部分、全连(Fully Connection,FC)部分、池化(Pooling, Pool)部分和激活部分。CONV部分中多层循环嵌套引入的大量计算操作是硬件加速器设计优化的主要难点。

AlexNet是一种典型的具有代表性的CNN结构，其网络组织完整地包含了上述4个核心部分。表1所示为AlexNet的网络结构参数，其中：输入/输出特征图数量为Nin/Nout，输入/输出特征图的尺寸为SIZEin/SIZEout，卷积核尺寸为SIZEker，卷积跨度为Stride，补零填充尺寸为Npad。相比于其他网络，AlexNet复杂多变的网络结构大大增加了硬件加速的难度。一些性能突出的CNN加速器明确表示，AlexNet多样的卷积形式不利于计算需求与计算资源的适配，因此这些加速器在加速AlexNet时难以实现与其他网络等同的卓越加速性能[3,13]。

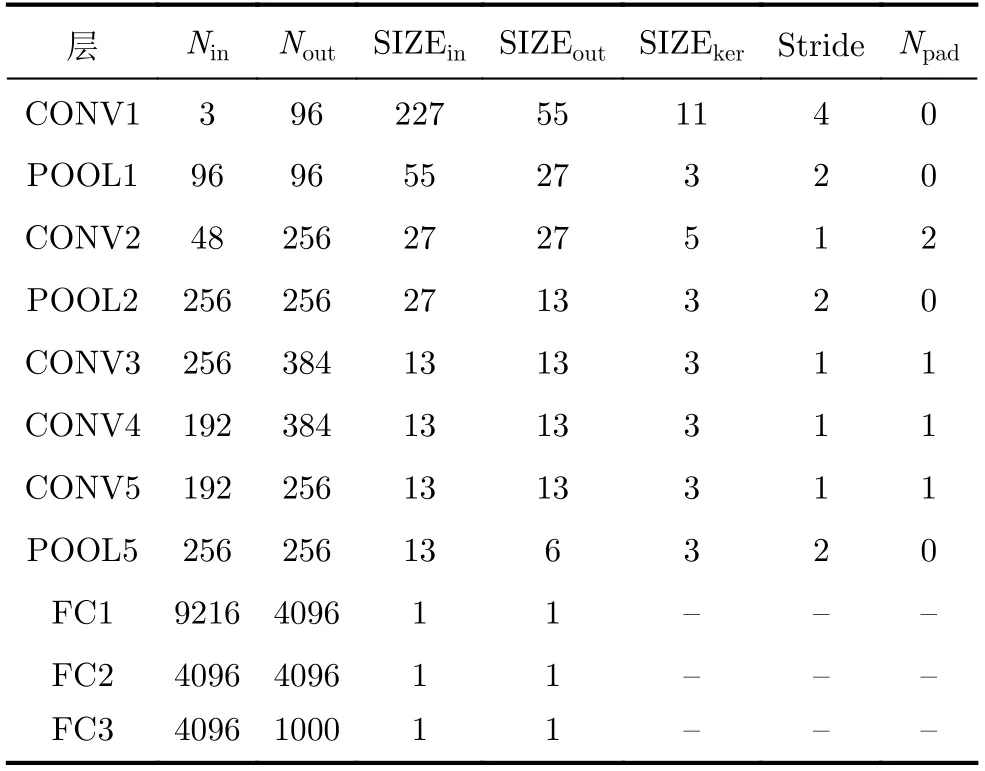
表1 AlexNet网络结构参数

基于以上分析，本文采用具有结构代表性的典型CNN AlexNet作为benchmark，通过验证的并行度确定算法能适用于绝大多数的CNN网络。此外，以AlexNet为benchmark能够更明显地反映并行度确定算法的优劣：若并行度确定算法在加速AlexNet时可以获得突出的加速效果，那么该算法在加速其他卷积结构更加单一、Nin/Nout更加规律的CNN网络时，同样可以获得良好的加速效果。反之，若算法在网络结构差异性上考虑不全面，即使其在加速部分CNN时可以获得不错的效果，其算法问题会在加速AlexNet过程中显示出来。

3 技术现状与问题分析

在加速CNN这类计算密集型网络时，如何高效利用FPGA片上的计算资源是设计的核心要点。本文采用文献[2]所提出的计算资源利用率作为评估指标。该指标有两个评估参数(R1, R2)，R1和R2的取值范围都是[0, 1]区间内的实数，其值越大代表资源利用越充分。R1衡量设计中FPGA的可用计算性能潜力被开发出的百分比，R2衡量设计中计算资源的冗余占用情况，R1的优先级高于R2。

表2为不同加速器的计算资源利用率情况。从表中可知，现有加速器的计算资源利用率普遍存在提升空间：其(R1, R2)结果均不够理想，或难以同时兼顾(R1, R2)达到理想值。同时，对比VGG和AlexNet加速器评估结果，AlexNet加速器的资源利用率普遍劣于VGG加速器—加速器的不足在AlexNet这样的benchmark上更为突出。

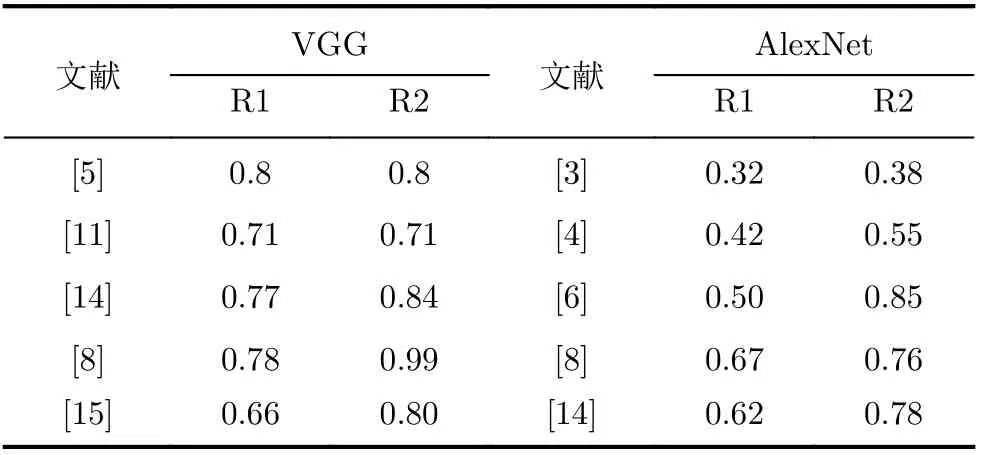
表2 不同FPGA CNN加速器的资源利用率

CNN中的核心计算为矩阵卷积计算。文献[2]具体分析并指出：卷积计算单元难以兼顾资源粒度和时间粒度的灵活性是阻碍FPGA充分发挥计算效力的重要原因。除此之外，有限的并行度调整空间也是限制计算资源充分发挥计算效力的重要原因。例如在文献[8]中，加速器各层只有输入并行度(Parain)和输出并行度(Paraout)两种维度可以调节，且Parain, Paraout的取值被严格限定为2的整数幂，这使得并行度增减的变化粒度过大，无法实现小幅度调节。相比其他CNN，这种粗粒度的并行度确定算法对AlexNet这类网络极不友好，主要表现为以下两点：

(1) AlexNet的首层输入特征图尺寸过大，仅采用Parain, Paraout来调节运算，单图计算时间粒度与资源粒度过大。

(2) AlexNet中大量卷积层的输入/输出特征图数目(如3, 96, 384, 192)都不满足2的整数幂，被限制为2的整数幂的并行度参数与这些层的特征图数目严重失配。

相比于AlexNet首层存在11×11这样的大尺寸卷积核，VGG的卷积核均为3×3的小尺寸，这更利于资源粒度和时间粒度的优化。此外，VGG中绝大多数层的特征图数目为2的整数幂，可与并行度参数良好适配。以上原因共同作用，导致AlexNet加速器的资源利用率普遍劣于VGG加速器。即便如此，VGG加速器的R1也主要分布在[0.6, 0.8]区间，难以达到≥0.9的理想资源利用率，计算资源的浪费仍然普遍存在。

基于以上分析，为解决计算资源浪费的问题，在文献[2]卷积计算单元粒度优化的基础上，本文聚焦于提出一种高效的细粒度并行度确定算法。该算法面向不同FPGA平台、不同CNN网络结构，通过灵活的并行度细粒度调节，可以显著提高计算资源利用率，最终实现突出的CNN加速效果。

4 细粒度可变换加速结构与并行度优化搜索算法

4.1 加速器硬件设计

本工作架构设计采用文献[2]所提出的硬件方案：加速器整体采用全流水结构，权重数据和输入特征图数据存储在片外，各层计算的中间结果以乒乓结构存储在片上，带宽需求最密集的FC层采用了批处理模式以降低数据传输带宽需求。

图1为加速器单层结构示意图，CNN中的各层通过层间存储相互隔离。来自本层存储的输入特征图数据，首先在卷积计算单元(Computing Element,CE)阵列中进行卷积运算。卷积的临时结果在第1级缓存中完成累加，产生卷积结果。卷积结果从第1级缓存传输到第2级缓存的数据转移过程中，会根据各层不同的需求完成激活和池化操作，产生单层运算的最终结果。第2级缓存的数据会被输出到下一层存储中，用作下一层网络计算的输入数据。

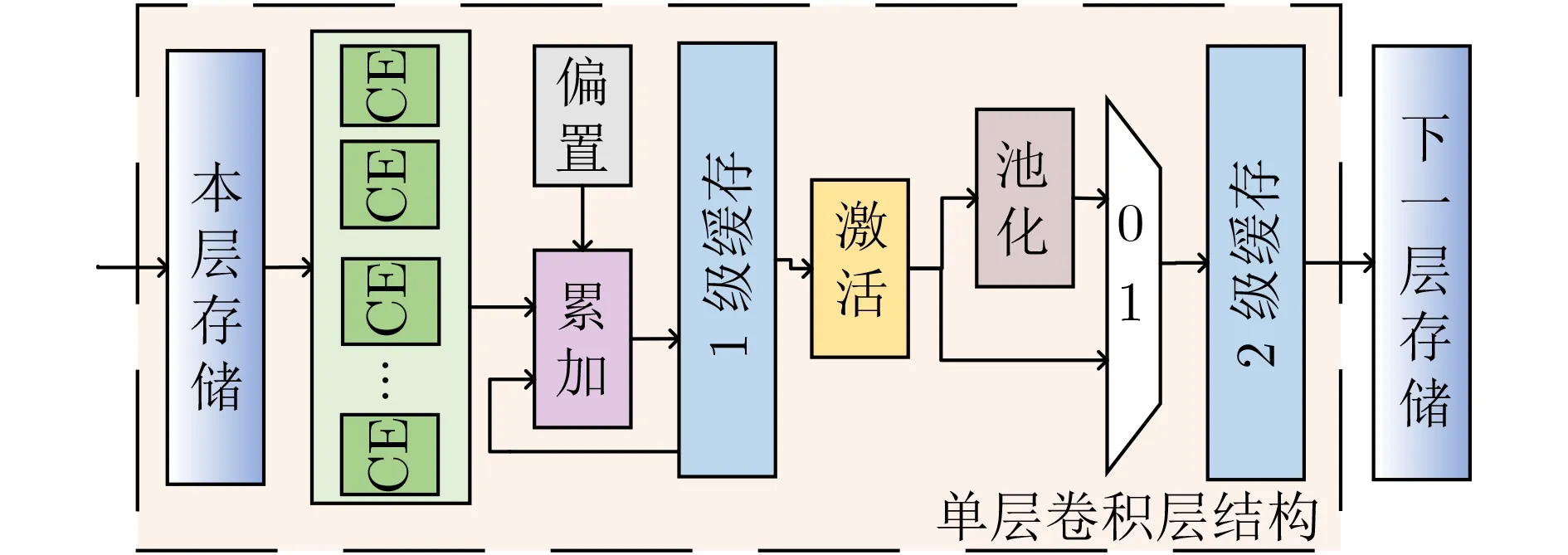
图1 CNN加速器单层结构示意图

文献[2]提出创新的3维可变换卷积计算结构以提高计算粒度灵活性。通过分析可知，基础CE的计算资源粒度为Gbasic= SIZEout·SIZEker，单层计算时间粒度为Tbasic= SIZEout·SIZEker。经过变形后，CE的计算资源粒度变为G= ROWout·SIZEker·Paraout，单层计算时间粒度为T= SIZEout·SIZEker·「SIZEout/ROWout⏋。ROWout比SIZEout更加灵活，代表变形后特征图片段的数据行数，其取值范围为[1, SIZEout]区间内的整数。ROWout和Paraout的配合共同实现了卷积计算结构资源和时间粒度灵活性的提升。

4.2 细粒度并行度优化搜索算法1)

4.2.1 问题模型

为延拓并行度搜索空间，文献[2]在传统Parain和Paraout2维探索空间外，拓展了并行度维度，引入了第3维并行度参数—特征图分割并行度Paraseg。如图2所示，一个矩阵卷积的计算过程可以被按行分割，切分为Paraseg个较小的矩阵依次进行卷积，其中Paraseg等于「SIZEout/ROWout⏋。ROWin表示需要被存储的输入特征图片段的行数，其值由式(1)确定。函数ξ当且仅当Paraseg为1时等于1，否则等于0。

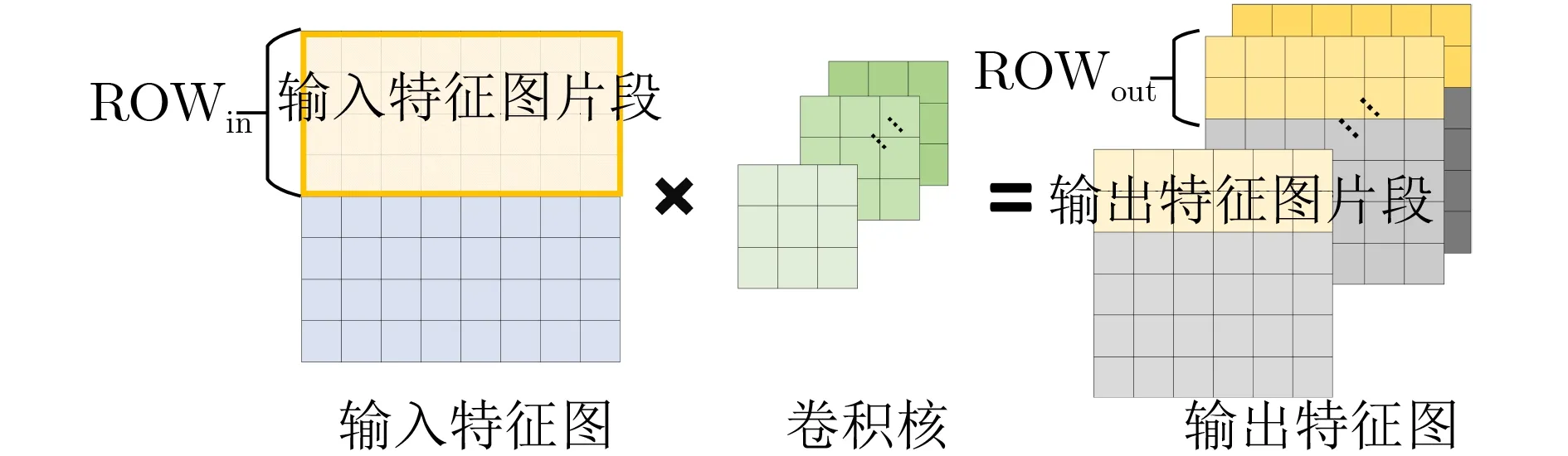
图2 矩阵卷积分段计算示意图

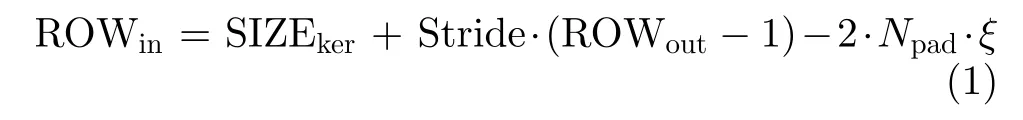
Paraseg的提出是为了从以下两个方面提升计算资源利用率。

(1) 针对特征图尺寸过大导致卷积计算资源粒度过大的情况，可以通过切割后依次处理特征图片段的方法，以较小的资源粒度完成整张特征图的卷积操作。

(2) 多数CNN网络的首层输入特征图为RGB 3通道，Nin=3。较少的Nin压缩了Parain的选择空间，为追求较高的资源利用率，Parain只能选择1或3。这严重限制了首层的资源规划空间。Paraseg的引入相当于将Parain的取值范围由整数域(1或3)延拓到分数域(例如1/2, 1/3, 3/5 ···2)(Parain=1, Paraseg=2)相当于Parain=1/2；(Parain=3, Paraseg=5)相当于Parain=3/5；以此类推。)，极大地拓展了资源规划空间。

为确定加速器的最优并行度配置参数(Parain,Paraout, Paraseg)，本文提出一种并行度优化搜索算法。其设计目标为：在取值区间内以最细粒度遍历所有可行的并行度组合方案，筛选出计算资源利用率最高的并行度配置参数。相比于传统的粗粒度并行度搜索算法，本文所述算法可以更加精细地调节资源分配，最终使得加速器实现理想的加速效果。

4.2.2 算法约束

本文在如下4条约束的基础上，按照表3所示方法确定3种并行度参数。为提高计算资源利用率，对单层计算资源使用量#DSPi、单层计算所需周期数#cyclei有约束1和2；受可用资源数限制，对#DSPi、单层存储资源使用量#BRAMi有约束3和4。

表3 细粒度并行度迭代算法

约束1 为保证资源分配的合理性，#DSPi与片上可用DSP总量(#DSPtotal)之比，应尽量接近该卷积层计算量(#OPi)占网络总计算量(#OPtotal)的百分比。

约束2 全流水加速器的吞吐率受限于最大#cyclei，为提高吞吐率，应尽可能减小max{#cyclei}。

约束3 ∑#DSPi应不超过片上可用DSP资源总数#DSPtotal。

约束4 ∑#BRAMi应不超过片上可用存储资源总数#BRAMtotal。

4.2.3 遍历求解

本文遍历搜索最优并行度方案的过程中，Paraseg的值由ROWout唯一确定。Parain, Paraout, ROWout的取值范围分别为[1, Nin], [1, Nout], [1, SIZEout]，三者的取值均能以1为最小步长细粒度地增减调整。第i层卷积层所需DSP资源数如式(2)所示，所需周期数如式(3)所示，所需BRAM存储资源数如式(4)所示。其中#cyclecntl代表控制逻辑所需周期数，CBRAM代表一个BRAM的数据存储容量。

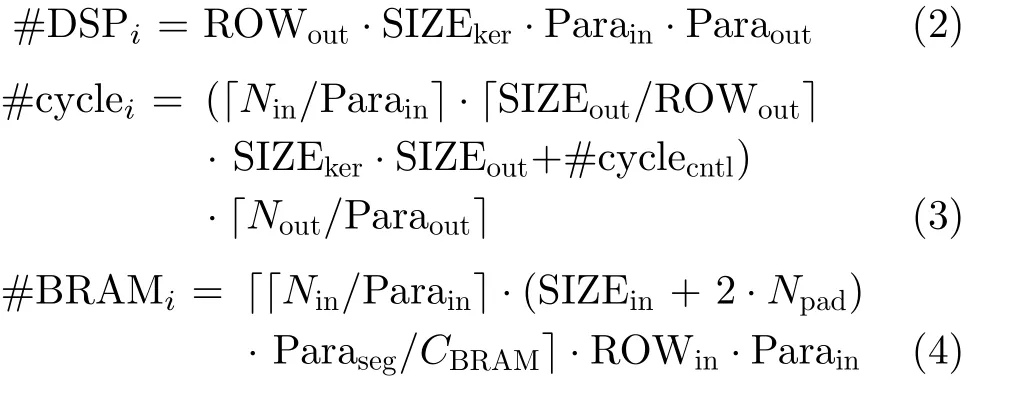
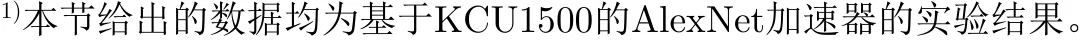
遍历开始之前，需要进行数据准备工作：指定#DSPtotal，并依据#OPi占#OPtotal的百分比进行DSP资源预分配，分配给第i层的DSP资源数为#DSPalloc i；指定#BRAMtotal；根据#OPtotal与#DSPtotal的比值确定理论最小计算周期数#cyclebaseline。在此基础上开始并行度细粒度遍历。

第i层中，以1为步长依次遍历元组(Parain,Paraout, ROWout)的所有有效取值，可以计算得到各种并行度组合方式下的单层加速器时间/资源开销情况的集合Si。根据约束1，Si中元素的挑选规则基于如下基本假设：#cyclei,j,#DSPi,j偏离#cyclebaseline, #DSPalloc i越远，其成为最优并行度方案的可能性越小。本文定义，α为计算周期浮动因子，β为DSP分配浮动因子。那么，对于Si中任意元素σi,j而言，需要满足约束(#c y c l ei,j/#cyclebaseline)落在区间[1–α, 1+α]内，且(#DSPi,j/#DSPalloc i)落在区间[1–β, 1+β]内。

为获得加速器时间/资源总开销，需要先计算集合Si(i=1 ～5)的笛卡儿积S(即S=S1×S2×···×S5)，S中的每个元素都对应一种跨层组合方案。遍历集合S，计算所有满足资源约束的元素对应的m a x{#c y c l ei}(i=1 ～5)，升序排序，min{max{#cyclei}}对应的元素即为加速器获得最佳性能/资源利用率所采用的并行度配置方案。

4.2.4 问题分析

在以上并行度遍历求解的过程中，细粒度调节在扩展搜索空间以提高灵活度的同时，也极大地增加了跨层全组合的计算需求。如图3所示，当β=0.20，α从0.02变化到0.28时，计算量从1.21×107增长到2.21×1012。其中，当α<0.16时，由于约束过紧，无法搜索到符合条件的并行度方案。当α=0.16时可以找到符合约束的并行度方案，此时计算量为1.34×1011。根据实验估算，即使是采用性能较好的CPU(Intel Core i7-8750H)，处理这样数以千亿的计算量也需要花费极长的时间(106h的量级)，这样的运行效率是不可接受的。

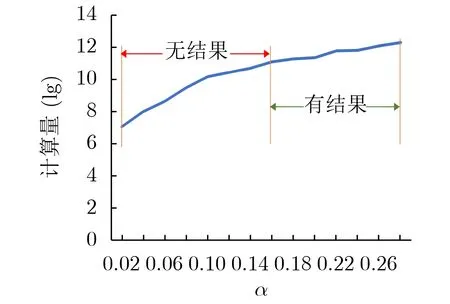
图3 β=0.20时，算法搜索的计算量随α的变化情况

基于以上对细粒度并行度参数求解规模的分析，为缩短遍历求解的执行时间，本文提出了一种并行度优化搜索算法。该算法可以在有限的片上可用资源的限制下，通过多轮数据清洗和计算剪枝的方法，快速产生可行的并行度方案，使得加速器整体资源利用率、吞吐率和性能功耗比等得到优化提升。

4.2.5 迭代优化

由于全组合的方案数据量极大、冗余计算多，从计算有效性的角度出发，本文工作提出以下3种优化方法，从各层筛选出真正可能影响最终计算结果的有效数据参与遍历，压缩计算量。由于单层Si集合中的元素数量较大，直接采用全局数据清洗比较耗时，故先采用3轮局部迭代清洗的方法进行数据粗筛，而后采用全局清洗的方法对数据进行精筛，最后在遍历计算的过程采用剪枝手段裁剪无效计算分支。

(1) 数据粗筛(3轮)：排序+局部数据清洗。数据粗筛共有3轮迭代过程，每轮迭代都分为排序和局部数据清洗两个步骤。

(a) 排序：对单层Si集合中的元素，第1轮迭代以#cyclei, #DSPi, #BRAMi优先级递减的顺序，将数据按照升序排列；第2轮迭代以#DSPi,#cyclei, #BRAMi优先级递减的顺序升序排列；第3轮迭代则是以#BRAMi, #cyclei, #DSPi优先级递减的顺序升序排列。排序是为了使得更优的并行度组合方法尽早出现，可以减少后续数据清洗所需的时间，也能让剪枝操作更加高效。

(b) 局部数据清洗：对于集合Si中的元素σj和σk(j≠k)，若σj的#cycle, #DSP和#BRAM均不大于σk的相应指标，定义偏序关系“KO”：元素σk“完败”(被“KO”)元素σj，元素σj“完胜”(“KO”)元素σk。对于每轮排序完毕的单层数据，进行一次局部数据清洗，即流式压缩遍历，比较相邻元素并剔除“完败”的。数据每经过1轮局部清洗，有序集合都满足如下条件：任意相邻的两个元素不存在“KO”偏序关系。

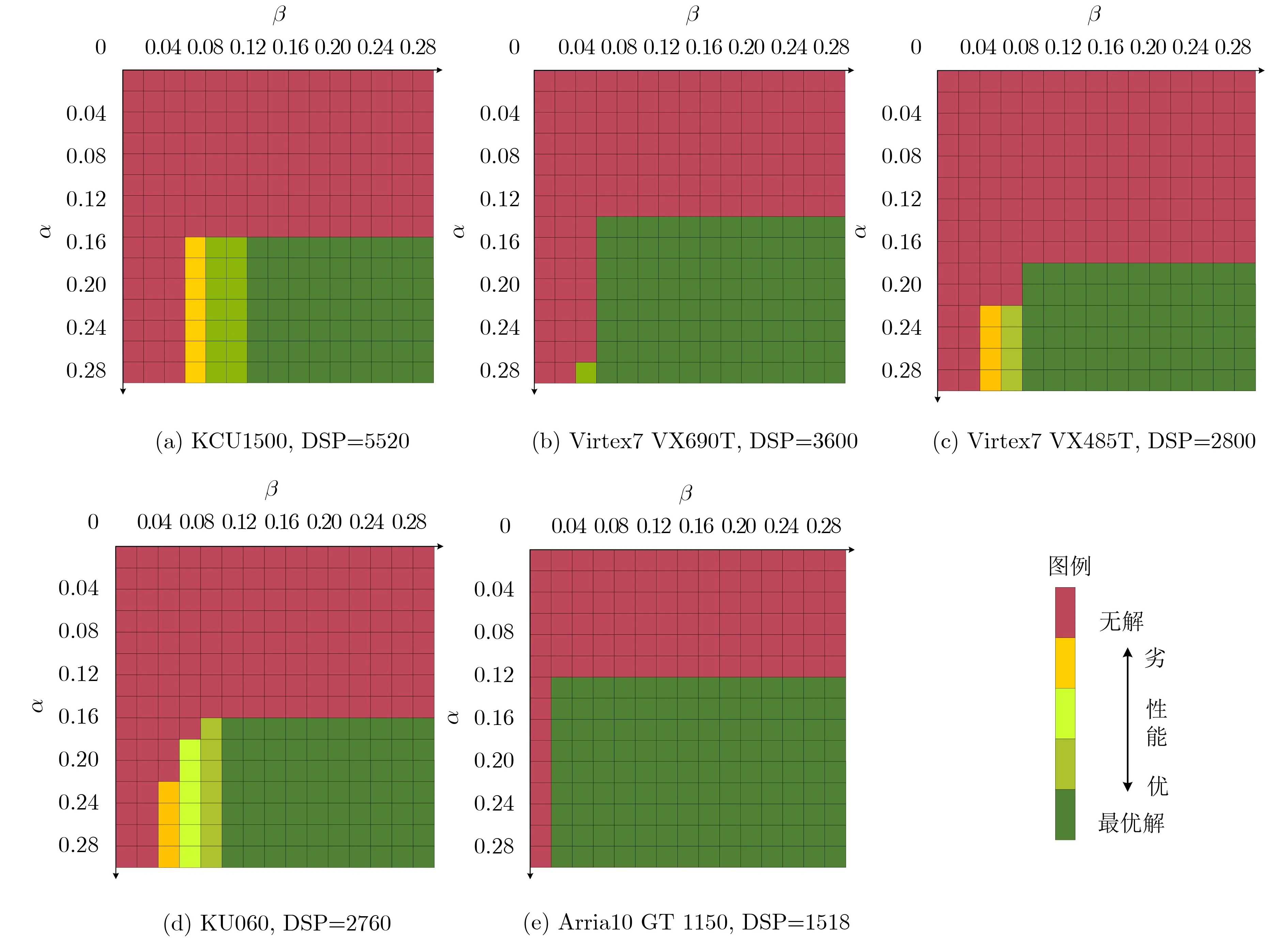
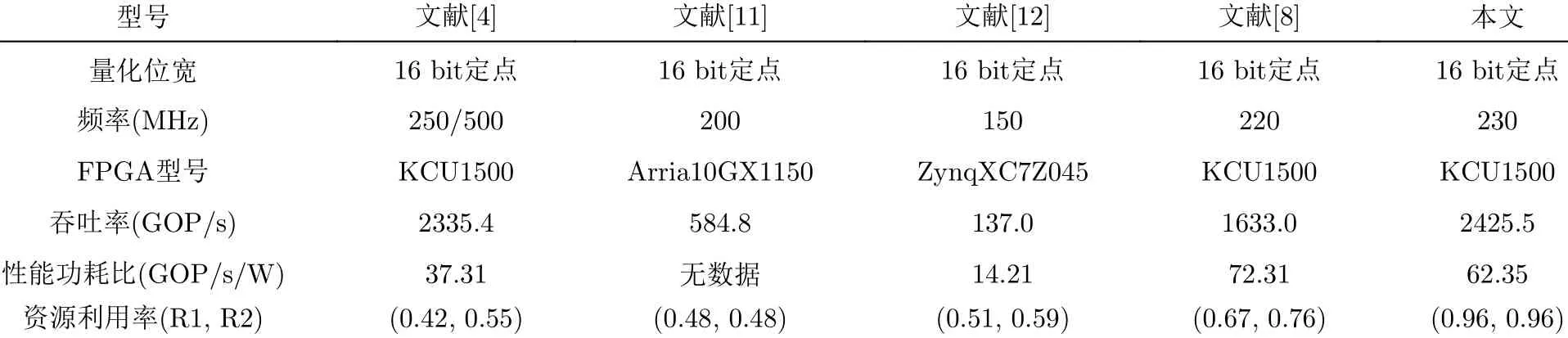
(2) 数据精筛(1轮)：排序+全局数据清洗。单层集合Si经过数据粗筛压缩后，得到的有序集合记为S’i，将其重新以#cyclei, #DSPi, #BRAMi优先级递减的顺序按照升序排列，并进行全局数据清洗：遍历S’i，若某元素σj“完败”排在其前面的某个元素σk(k

当(α, β)等于(0.2, 0.2)时，上述数据3轮初筛和1轮精筛分别可以将集合Si中待迭代处理的数据量从2.43×1011锐减为7.10107, 4.12×106, 3.53×106,7.22×105，最终高效压缩了99.9997%的数据量，显著降低了算法后续的计算量。

(3)搜索剪枝：经过上述粗筛和精筛两步数据清洗，极大地压缩了单层数据量，然而在较松的α和β约束下，跨层全组合的方式仍然有着不小的计算量，需要在遍历时进行剪枝优化。

(a) 从外(第1层)到内(第5层)的嵌套循环遍历过程中，实时计算并更新跨层组合方案已经使用的DSP和BRAM个数。若计算到某一层，资源使用已经超标，则直接跳过后续所有内层循环，将该分支的跨层组合方案全部裁剪。

(b) 实时更新已遍历的跨层组合中最优的max{#cyclei}结果(记为maxCycle)。在后续循环过程中，如果当前层的#cycle大于maxCycle，意味着该组合分支无法进一步优化maxCycle，停止往内层继续遍历，将该分支对应的跨层组合方案全部裁剪。

在前文所述(α, β)=(0.2, 0.2)的配置下，上述3种优化可以将细粒度遍历迭代优化搜索算法所需的计算时长从106小时量级，显著降低到8.115秒，有效提高了算法的可行性。

5 实验与分析

5.1 实验配置

本实验CNN数据量化为16 bit定点数，综合及实现软件为Vivado19.2，CPU为Intel Core i7-8750H。为降低布局布线的难度、保证工程实现的可行性，实验限制BRAM资源的使用率不得超过60%。

5.2 实验结果与理论分析

(1) (α, β)与搜索空间压缩：鉴于#cyclebaseline是理论最佳值，max{#cyclei}与#cyclebaseline的差值是客观存在的。在资源限制下，本文所述算法的优化目标是尽可能减少二者之间的差值。通过调整α取值，可以初步将max{#cyclei}限制在理想的区间，快速锁定合理的并行度组合范围。

不同FPGA平台的资源量千差万别，完全按照各层计算量占比进行分配的计算资源规划方式很难完全契合CNN网络的计算需求。而在实验过程中发现：若在单层#DSPalloc的基础上额外分配少量的DSP资源，则存在一定概率找到明显更优的并行度方案；若在单层#DSPalloc的基础上微量减少分配的DSP资源，则单层最优并行度方案存在一定概率不被干扰。调整β的取值可以弹性拓展各层DSP资源分配空间，以此在各层之间小幅流动DSP分配，达到优化max{#cyclei}的目的。同时，β的取值可以限制单层使用的DSP资源数在#DSPalloc上下以β为百分比浮动，将资源分布严重偏离计算量分布的并行度组合方式删除，保留资源分布更加合理的并行度组合范围。

合理设置(α, β)可以有效限制最优并行度的搜索空间，减少后期迭代遍历所需的计算量。以KCU1500开发板加速AlexNet为例。若没有(α,β)的限制，集合Si(i=1～5)的笛卡儿积S将是一个巨大的探索空间，包含1024数量级的元素。然而，其中绝大多数元素都对最终搜索结果没有影响。若将(α, β)设置为(0.2, 0.2)，则可将S中的元素数锐减到1011数量级，压缩了超过99.99%的计算量。

为进一步探索不同(α, β)约束对并行度方案性能的影响，本实验将上述算法应用于不同规格的FPGA芯片，并将不同(α, β)约束下探索到的最优并行度方案按max{#cyclei}进行排序。实验结果如色温图4所示，(α, β)沿右下增长，标注颜色从绿到红代表并行度方案从优到劣。

从图4分析可得，较严格的(α, β)约束可以通过快速排除违例的并行度方案而大大压缩计算量，但是过分严格的约束会带来找不到可行方案的风险。宽松的约束将大量并行度方案保留至迭代搜索中，更大的搜索空间提高了找到最优解的可能性。然而，当(α, β)到达临界值后，增大(α, β)并不会带来并行度方案的优化。这是因为：过大的α所额外拓展的搜索空间内，#cyclei的方差随α的增大而增大，这会造成max{#cyclei}的恶化，导致加速器吞吐率下降；过大的β所额外拓展的搜索空间内，各层#DSPi的分布更加偏离约束1的限制，导致该额外搜索空间内并行度方案的DSP资源利用率明显下降。从图4(a)—图4(e)可知，(α, β)取值为(0.18,0.12)时可以在最少计算量下找到最优的并行度方案，该值即为(α, β)的临界值。

图4 基于不同规格FPGA的AlexNet加速器性能随(α, β)变化色温图

(2) 迭代优化与快速查找：在该临界值(α, β)的约束下，搜索空间内依旧存在大量冗余元素，它们的性能虽然较好，但并不足以改变最优并行度方案。因此算法提出数据筛选优化的方法，通过多轮迭代筛选可以将真正关键的元素挑选出来，同时进一步高效压缩了计算量。不同规格AlexNet加速器的实现情况如表4所示。表4中原始计算量代表在临界(α, β)约束下未经数据筛选的计算量。经过数据筛选后，超过99%的原始计算量被压缩。

算法在数据筛选后，通过剪枝的方法裁剪掉无效计算分支，可以加速遍历搜索速度。表4中执行时间代表CPU遍历搜索所需的时长，单位为s。经过剪枝优化后，遍历搜索所需的时长从106小时量级减少到平均4.944 s，极大地降低了算法的时间开销。

(3) 实验结果与对比分析：该实现方案可以灵活调节以适应不同规格开发板的资源限制，最终得到稳定突出的加速性能。如表4所示，采用本文所述的计算结构与并行度优化方案，在不同资源规格的FPGA开发板上实现AlexNet加速器，其计算资源利用率(R1, R2)平均可达(0.957, 0.962)。这进一步验证了文献[2]中卷积结构的灵活性和本文所述算法的鲁棒性。

表4 不同规格FPGA上AlexNet加速器资源利用率、计算量与计算时长

基于FPGA的CNN加速器的加速效果与并行度确定算法的优劣直接强相关。因此，可通过对比加速器性能参数，可直观反映并行度确定算法的搜索效果。实验将本工作加速结果与不同CNN加速器的性能进行对比，具体参数如表5所示。本工作计算资源利用率达到(0.955，0.962)，在230 MHz下实现了2425.455 GOP/s的吞吐率、62.351 GOP/(s·W)的性能功耗比。相比其他基于FPGA的AlexNet加速器[4,11,12]，本工作实现了吞吐率和性能功耗比的明显优化。相比文献[2,8]在具体硬件结构优化上侧重有所不同，其首要优化目标为吞吐率，因此，本工作的性能功耗比为文献[8]的86.226%。但是得益于资源利用率的优势，本工作的吞吐率是文献[8]的1.485倍。相比现今AI加速领域最高效的GPU平台Nvidia Jetson TX2，本工作有6.821倍的单图处理速度提升及1.876倍的单图处理功耗优化。

表5 AlexNet加速器性能对比

(4) 总结分析：文献[2]所提出的卷积计算结构拥有极高的灵活性，可通过结构变换满足资源限制和计算需求。随着结构灵活性的提高，其对应并行度方案的搜索空间显著扩大，但也伴随着计算量爆炸式增长的问题。该原始搜索空间内包含大量冗余元素，这些元素对应的性能指标不仅较差，还会引入巨大的无意义的计算代价。为了压缩搜索空间，本文所述算法利用(α, β)将搜索空间限制在其合理的子空间内。然而，子空间内的元素规模依旧非常可观，且其中大量元素虽然性能较好，但仍然不会对最优并行度方案起决定作用。因此算法提出多轮迭代数据筛选优化，可以将真正关键的元素挑选出来，同时进一步高效压缩了计算量。最后，算法在数据遍历搜索环节采用剪枝的方法，裁剪无效计算分支，在(α, β)典型值的约束下，将最优解搜索时间控制在10 s内。通过硬件结构与并行度算法的配合，本工作可以快速实现CNN硬件加速器，其加速性能稳定且突出。

6 结束语

为提高加速器性能，文献[2]提出了一种高度灵活的计算结构，这导致并行度探索空间爆炸增长。为快速在搜索空间中得到计算资源利用率最优的并行度组合方案，本文提出一种迭代优化搜索算法。该算法通过多轮迭代的数据筛选和剪枝操作，成功地压缩了99%以上的搜索空间，将计算所需时长从106h量级减少到10 s内。实验证明该算法具有普适性，可适用于不同规格的FPGA芯片，最终实现平均(0.957, 0.962)的计算资源利用率。本文在Xilinx KCU1500开发板完成AlexNet加速器板级验证，在230 MHz频率下实现了(0.955, 0.962)的计算资源利用率、2425.455 GOP/s的吞吐率、62.351 GOP/(s·W)的性能功耗比。本文相比于其他FPGA CNN加速器[4,11,12]实现了吞吐率和性能功耗比的明显优化，相比于现今AI加速领域最高效的GPU平台Nvidia Jetson TX2实现了6.821倍的单图处理速度提升及1.876倍的单图处理功耗优化。