基于改进矩阵束的超宽带一维散射中心提取方法

魏少明 洪文衍 王 俊 耿雪胤 金明明

(北京航空航天大学电子信息工程学院 北京 100191)

1 引言

散射中心特征模型能够刻画目标的细节信息，因而得到广泛应用[1–5]。在高频区超宽带(Ultra Wide Band, UWB)条件下目标电磁散射可以近似为各散射点局部电磁散射合成[6]。目前用于描述超宽带雷达散射中心特征的模型主要有指数和模型、衰减指数和几何绕射(Geometrical Theory of Diffraction,GTD)模型。其中GTD模型基于几何绕射理论，以高频散射的局部性原理为基础[7–9]加了频率依赖的散射强度指数变化项，能够表征散射中心位置、散射强度、频率依赖因子信息，更接近目标实际的散射机理。类型参数(频率依赖因子)能够反映边沿、曲面、锥形、直边、凹槽等目标典型结构，具有明确的物理意义。

针对此类模型参数估计问题，国内外研究者主要采用常规的Prony方法、矩阵束法、ARMA 模型、ESPRIT和MUSIC算法、Cauchy方法[10–12]等。这些方法主要用于计算散射中心的位置、强度和衰减因子，但大都无法反映不同的散射中心频率依赖特性。近年来，出现了很多基于模型的特征分解方法，一般采用状态空间法来实现系统的识别和对目标散射参数的提取。文献[13]首先采用状态空间法对时序数据进行处理来估计衰减正弦信号的频率和散射强度。文献[14–17]利用状态空间法提取散射中心的散射强度、衰减速率和径向距离信息。文献[18]结合几何光学(Geometrical Optics, GO)、GTD模型，推导了频率依赖因子数学表达式，可应用于正向参数化建模中的频率依赖因子的正向推算。文献[19]提出了一种基于状态空间法的目标重构算法，证明了状态空间法在重建散射强度和散射中心上具有优势，并且该方法可以降低参数对噪声的敏感性。文献[20]提出了一种基于简化奇异值分解的状态空间法，利用最大似然估计求解散射中心强度。文献[21]采用基于多级快速多极子算法的有效数值方法求解电磁散射问题，获得可靠的散射数据，并且引入了信息论的压缩感知理论，加快了计算速度。文献[22]基于EM(Electro Magnetic)模型，利用状态空间法对步行人体进行超宽带多普勒雷达信号压缩分析。文献[23]基于矩阵束算法等参数估计算法，实现了雷达目标结构成像。文献[24]基于矩阵束方法进行改进，对矩阵元素做了累积采样处理，实现了双重抗噪性能，更加准确地估计出多正弦信号的频率。

矩阵束法与状态空间法类似，都是以奇异值分解和特征分解为基础，但差异是，两种方法对参数的估计流程和精度不同，状态空间法采用特征值来求取系统极点，而矩阵束法则采用广义特征值来求取，估计精度方面，矩阵束法优于状态空间法。但矩阵束法构造的矩阵维数过高，导致计算量大、实现成本高，因此需寻找快速估计方法。本文将研究状态空间法和矩阵束法对散射中心参数估计过程的差异，并融合两种算法的优势形成一种性能和运算速度更为优越的改进矩阵束的超宽带散射中心提取算法。

本文的结构安排如下：首先给出超宽带雷达的GTD回波模型，并将宽带回波模型转化为状态空间表达形式。然后对回波进行汉克尔矩阵构造，利用奇异值分解将汉克尔矩阵中的噪声分量去除，并结合状态空间法将特征矩阵降维，通过特征值分解即可获得径向距离的估计；利用径向距离的估计结果，通过最小二乘算法可以进行类型参数的估计；最后通过最小二乘算法可获得散射强度的估计。矩阵束法和状态空间平衡法的实现流程相同，只是具体实现算法上，矩阵束法更为精准；针对矩阵束法中特征值分解矩阵的维数过大，提出了改进的矩阵束法，减少了特征值分解矩阵的维数大小。最后通过仿真验证了算法对微动参数估计的有效性。

2 超宽带回波信号建模和状态空间预处理

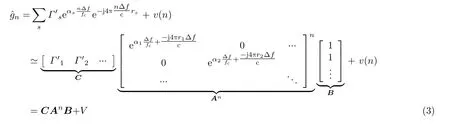
在高频区超宽带条件下目标的电磁散射可以认为是各散射点局部电磁散射的合成，根据几何绕射理论(GTD)，目标各散射点合成的频域回波模型可以表示为

3 基于改进矩阵束的参数快速估计方法

基于改进矩阵束的参数快速估计算法流程如图1所示。首先雷达接收回波数据，利用回波数据分别构造汉克尔矩阵H0与H1，对汉克尔矩阵做SVD分解，并将噪声部分截断。状态空间平衡法是根据状态空间模型来分解Hankel矩阵，而矩阵束算法是利用回波数据模型造成的矩阵间特殊关系来分解Hankel矩阵，从而把求解模型极点问题转换为求解广义特征值问题。本方法利用状态空间平衡法的矩阵分解思想进一步降低矩阵维数，降低矩阵束算法中特征分解的计算量，对降维后的矩阵特征分解，得到目标散射中心估计结果。

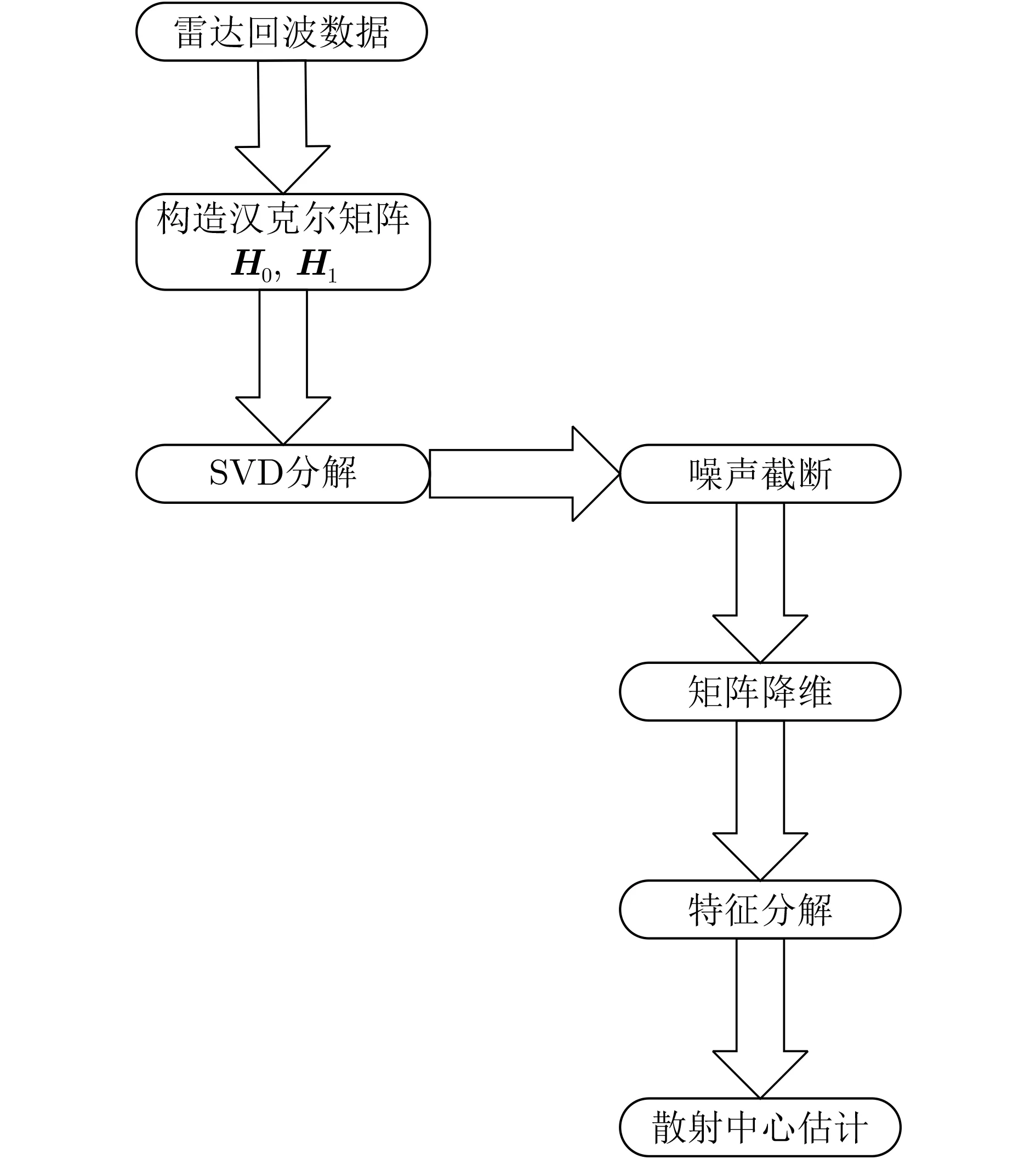
图1 改进矩阵束参数快速估计算法流程

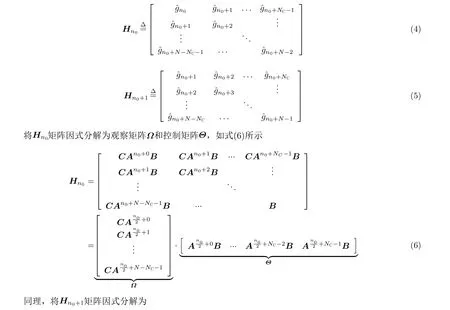
3.1 汉克尔矩阵的构造

3.2 径向距离的估计

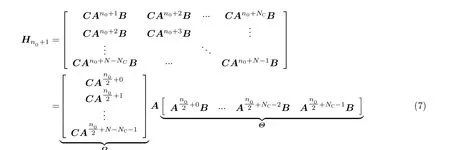
矩阵束算法的基本思想是构造两个特殊的Hankel矩阵，利用矩阵间的数学关系，通过求解汉克尔矩阵的广义特征值来求解系统极点，将模型估计问题转换为广义特征值问题，使得问题容易求解，利用所得极点可以获得目标回波的径向距离估计。由式(6)和式(7)可得

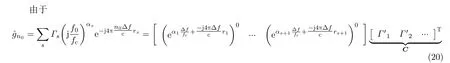
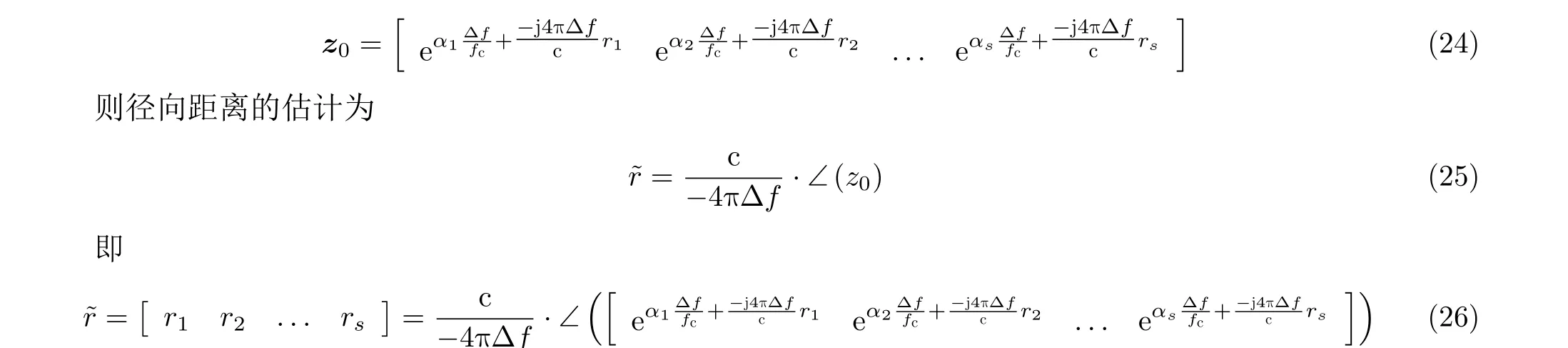
3.3 类型参数的估计

表1 类型参数代表的几何特征

3.4 散射强度的估计

式(2)的表达式可以写为

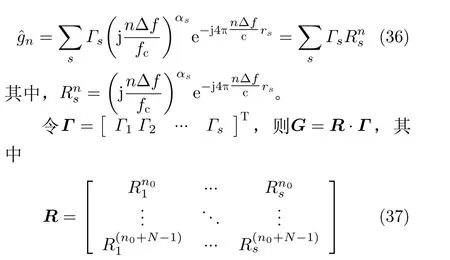
利用最小二乘估计，可得Γ=(RHR)−1RHG。再由式(27)和式(35)，可得R的估计

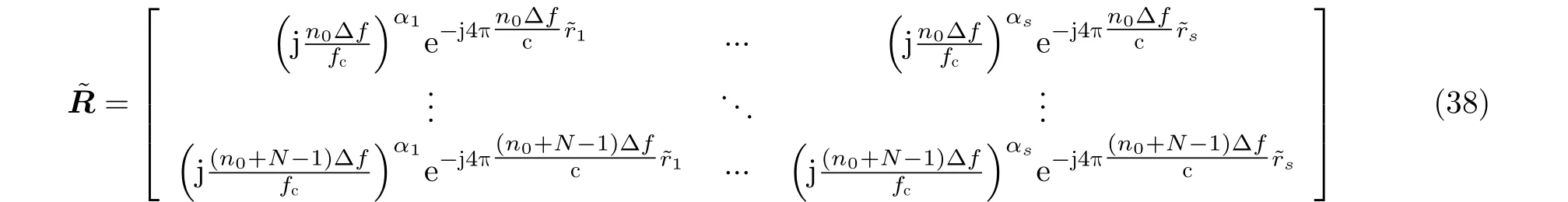
4 仿真验证

4.1 仿真设置

表2 散射中心参数估计的仿真参数设置

4.2 仿真数据

本节主要仿真暗室测量中状态空间平衡法、矩阵束法和改进的矩阵束法等3类方法对目标散射中心的提取结果，在扫频回波里加入信噪比为15 dB的噪声。

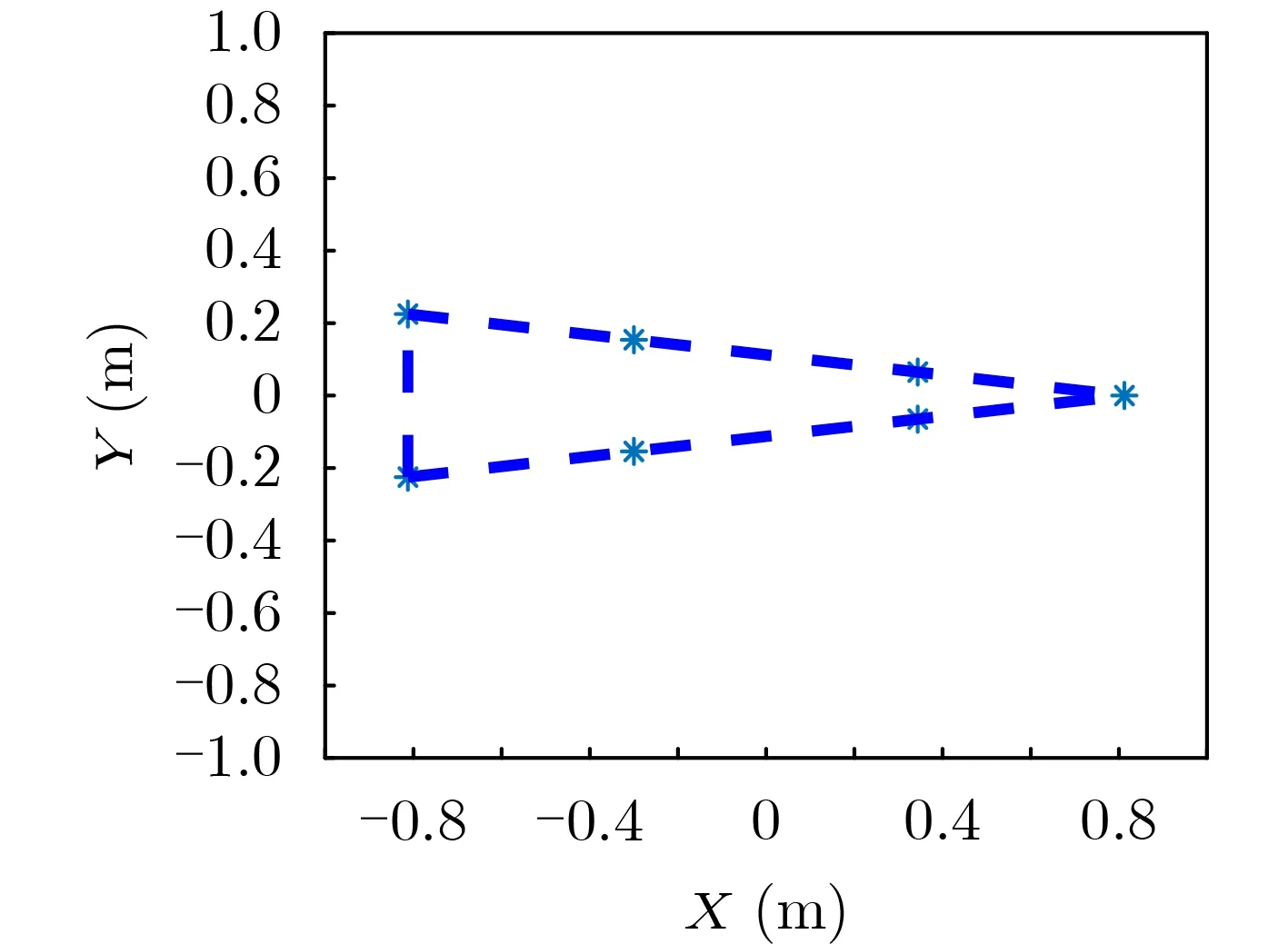
图2 球头锥目标的切面及散射中心的位置图像

图3为状态空间平衡法对径向距离-散射强度、径向距离-类型参数的提取图。

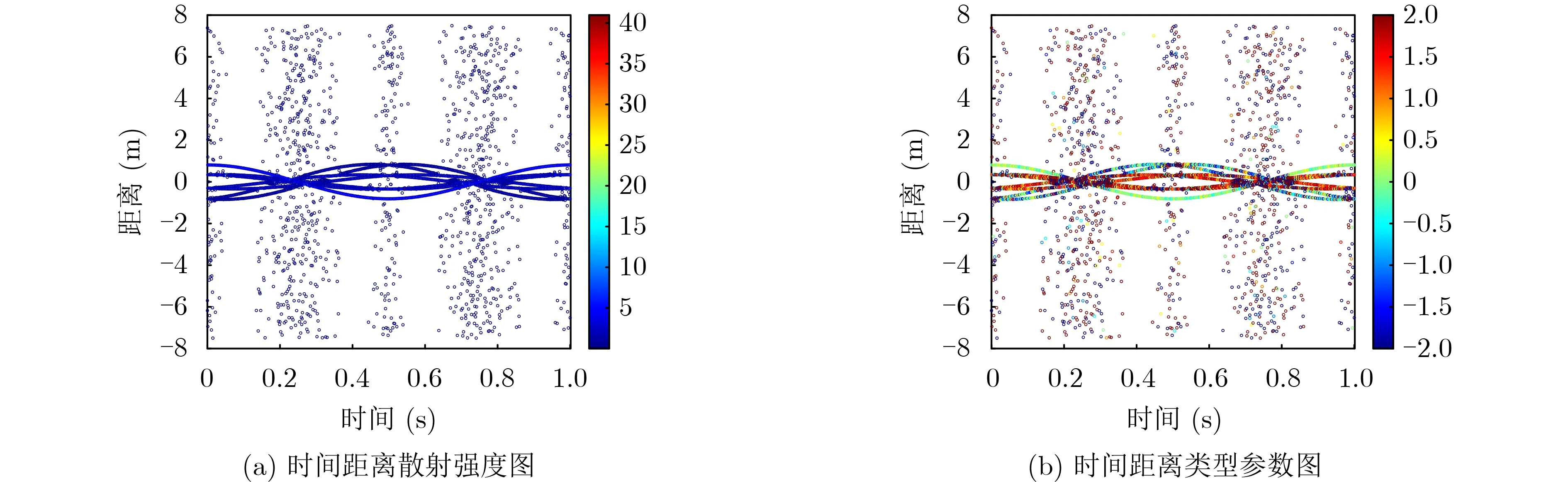
图3 状态空间平衡法对散射中心各参数的估计结果

图4为矩阵束法对径向距离-散射强度、径向距离-类型参数的提取图。

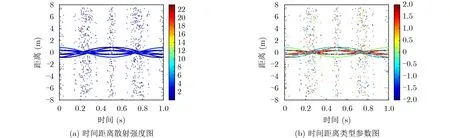
图4 矩阵束法对散射中心各参数的估计结果

图5为改进的矩阵束法对径向距离-散射强度、径向距离-类型参数的提取图。

从图3—图5可以看出，在加噪声的情况下，3种方法对径向距离、类型参数的估计精度较为接近，但是对散射强度的估计精度不一样。状态空间平衡法对散射强度的估计误差要大于矩阵束和改进的矩阵束方法对散射强度的估计结果。

图5 改进的矩阵束法对散射中心各参数的估计结果

表3为加噪声情况下，各算法的类型参数估计准确率与算法运行时间。

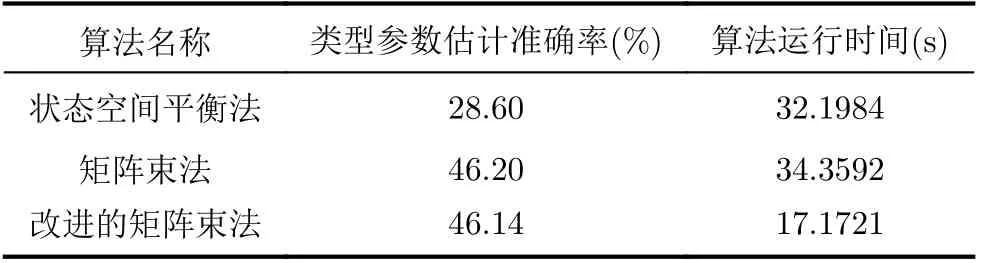
表3 加噪声情况下各算法的类型参数估计准确率及算法运行时间

从图6可以看出，3种方法对径向距离和散射强度估计的均方根误差都逼近CRB，对类型参数和相位偏移估计的均方根误差则都低于CRB。从运行时间来看，状态空间平衡法与矩阵束法基本一致，但是改进的矩阵束法比前两者快了50%左右。从类型参数的估计准确率来看，无噪情况下，3种方法的估计准确率基本一致；但是加噪声情况下，矩阵束方法和改进的矩阵束方法完全一致，都比状态空间平衡法高出18%。综合来看，相比状态空间平衡法与矩阵束法，改进的矩阵束法的鲁棒性更强、同时运算时间更快。

图6 3种参数估计方法的均方根误差

5 结束语

本文针对微动参数的高精度快速估计问题，结合传统矩阵束与状态空间方法的特性，提出了基于改进矩阵束的参数快速估计方法，该方法将GTD模型转化为状态空间模型，通过对矩阵降秩处理，提高了参数估计的速度。仿真验证了3种方法的性能，在多散射中心的情况下，矩阵束和改进的矩阵束方法对散射强度和类型参数的估计精度优于状态空间平衡法的估计结果。矩阵束法和改进的矩阵束法对参数的估计精度基本一致，但改进的矩阵束法的运算时间仅为矩阵束法的50%左右。整体来看，基于GTD模型的改进矩阵束参数快速估计方法能够快速、超分辨、高精度地提取出目标的微动参数。