采用模糊k核多粒度分解机制的高效社区发现

李宏平，刘 群

(重庆邮电大学 计算机科学与技术学院，重庆 400000)

0 引 言

社区结构的发现对于理解复杂网络中的结构有重要作用[1-4]。Newman算法[5]在传统算法的基础上大幅度降低了运算时间，使得社区发现不再局限于小规模网络。louvain算法[6]进一步优化了大规模网络图上的社区发现运算时间。LPA算法[7]通过少量预定义社区标签预测其余大部分未定义节点的标签，实现对大规模网络的快速社区划分。Walktrap算法[8]采用计算节点间的相似性的方式高效地捕捉各种规模网络的社区结构。贝叶斯模块选择算法[9]能高效、可解释地计算出节点的社区分配以及社区的最佳数量。虽然上述方法对时间复杂度有所降低，但是它们的计算时间与节点数量的关系密切相关，仍然需要花费较多的计算时间，尤其对于规模较大的网络，问题更加显著。可见，如何在减少社区发现算法运算时间的同时保证社区发现的精确度是社区发现领域还存在的一个问题。

针对上述问题，本文提出了一种基于模糊k-core的社区发现算法，首先使用k-core子图代表整个社区结构的分布，以减少社区划分的运算时间；在传统k-core分解的基础上运用模糊理论的隶属度函数得到模糊k-core子图，最大可能地保留高重要性节点，对模糊k-core子图进行社区划分，并将划分结果合理有效地扩散到其余节点，以保证社区发现准确度。实验结果表明，本算法在不同规模的真实网络数据集上与以上大部分算法相比，在减少运算时间的同时保证了社区划分的准确性，体现出了较强的综合性能。

1 相关知识

1.1 k-core分解

k-core分解可以区分不同节点的结构重要性并保留节点的邻域关系。该方法递归删除度数小于k的节点，直到所有其余顶点的度数都大于或等于k。k-core分解是一种基于节点的度，以提取核心节点集为目标的算法。

定义1 图的凝聚度：表示一个图网络中节点与节点之间联系的紧密程度，通常由连通度和直径这两个度量指标进行衡量，其中连通度是将一个连通图转变为非连通图所需要删除节点数的最小值，直径是任意两节点之间最短路径的最大值。图的凝聚度与连通度成正比，与直径成反比。

定义2 k-core：存在一个图G(V，E)，V表示节点集，E表示节点间的边集，d(v)表示节点v的度数。假设H是G的一个子图，δ(H)表示H子图的最小度，H中的每一个节点都至少有δ(H)个邻接点；若H是G的一个引导子图且δ(H)≥k，不包含于其余任意一个最小度大于等于k的引导子图，则H子图为图G的一个k-core，用KG(V，E)表示[10]。

定义3 k-remainder：由k-core得到(k+1)-core的修剪过程中被删除的节点集[10]。Rk表示节点集，rk表示相应的节点数。

图1用不同的空心圆(分别为J1,J2,J3)显示k值分别取1、2、3时的k-core。由于任意节点v的d(v)≥1，所以每个节点都属于1-core(由J1包围)，R0为空集，r0=0。递归删除d(v)<2的节点(圆形)后，其它节点d(v)≥2，形成2-core(由J2包围)，同时被删除的所有节点构成1-remainder，由R1表示，R1=15。进一步的修剪可以识别由三角形节点集所组成的3-core(由J3包围)，同时在修剪过程中被删除的所有菱形节点构成2-remainder，由R2表示，R2=5。此时，如果继续修剪，在从3-core中得到4-core的过程中，所有三角形节点都将被删除，所以图1的kmax=3，且三角形节点构成3-remainder，由R3表示，R3=9。从图中可以明显看出，如果一个节点属于3-core，则它也属于2-core和1-core。根据以上例证可以看出，处于核心位置的节点往往具有较高的k值。

图1 k-core分解

定义4 核塌缩序列：CCS(core collpase sequences)[10]可以直观展现一个图网络的凝聚度分布，表示为 {Rk/|V(G)|}，其中|V(G)|为图G的总节点数，k值上限为图G所包含的最小k-core的k值。以图1为例，整个图网络的节点总数为30，其中R0=0，R1=15，R2=5，R3=9，则该网络的CCS为 {0，1/2，1/6，3/10}。

k-core分解可以将网络划分为凝聚度不同的子网。k值越大，子网的凝聚度就越高。CCS直观地展示了凝聚度从弱到强的子网在整个网络的规模占比，反应了整个网络图的节点分布结构。

本文在传统k-core分解的基础上采用模糊k-core分解的方法，使更多的高重要性节点得以保留在k-core子图中。

1.2 传统模糊理论

模糊集理论对经典集合理论的扩展，最主要的贡献在于引入了集合中元素对该集合的隶属度[11]。

定义5 隶属度：主要通过隶属函数A(x)表示。用取值于区间[0，1]的隶属度函数A(x)表征x∈A的程度高低。A(x)越接近于1，表示x∈A的程度越高，A(x)越接近于0表示x∈A的程度越低。

“粒度”源于模糊集理论[12]，对于粒度的计算是一种来自不同层次，不同视角的思维方式[13,14]。k-core中也存在粒度，其将原始网络划分为多个子网络，每个具有不同k值的子网都代表一个粒度层。k值越大，子网中的节点数越少，子网中的节点重要性越高。

本文通过使用模糊k-core分解，将原网络划分为多粒度网络，相较于传统k-core分解的严格划分，此多粒度网络能更大程度地保留高重要性节点，更能从局部体现整个网络的社区分布。

2 基于模糊k-core的社区发现算法设计

2.1 问题描述

整个算法包括模糊k-core分解，子图社区划分和社区标签扩散3个步骤。首先对目标图网络进行模糊k-core分解，得到整个网络的核心节点集(即模糊k-core子图)；之后对核心节点集进行社区划分，使每个节点得到社区标签；最后将社区标签扩散到网络中其余所有节点，完成整个网络的社区划分。大致流程如图2所示。

图2 算法流程

2.2 模糊k-core分解

尽管k-core表示的概念很明确，每个节点与集合的隶属关系也很清楚，可以很好地将重要性不同的节点划分为不同的网络层，但是k-core分解在捕获节点重要性方面存在一些问题，即其递归修剪过程过于严格，导致一些重要性高的节点没有保留在k-core网络中。由于并非所有概念都适合进行清晰的划分，为了捕获更多的高重要性节点，本文提出基于k-core分解的模糊划分。

如图3所示，要获得2-core子图，就必须在经过递归修剪过后，所有节点的度数都大于或等于2。图3(a)描述了从1-core到2-core的第一次修剪过程。图3(b)为经过完整递归修剪过后的2-core子图。在原始网络G中，d(v1)=6，d(v2)=7，两个节点的度数在图G中属于较大范畴，表明节点v1和v2在网络中是高重要性节点。但根据k-core分解的定义，节点v1和v2在2-core的生成过程中将被删除。为了更好地筛选出高重要性节点，需要在k-core分解算法基础上，采用模糊函数对节点进行二次判断。

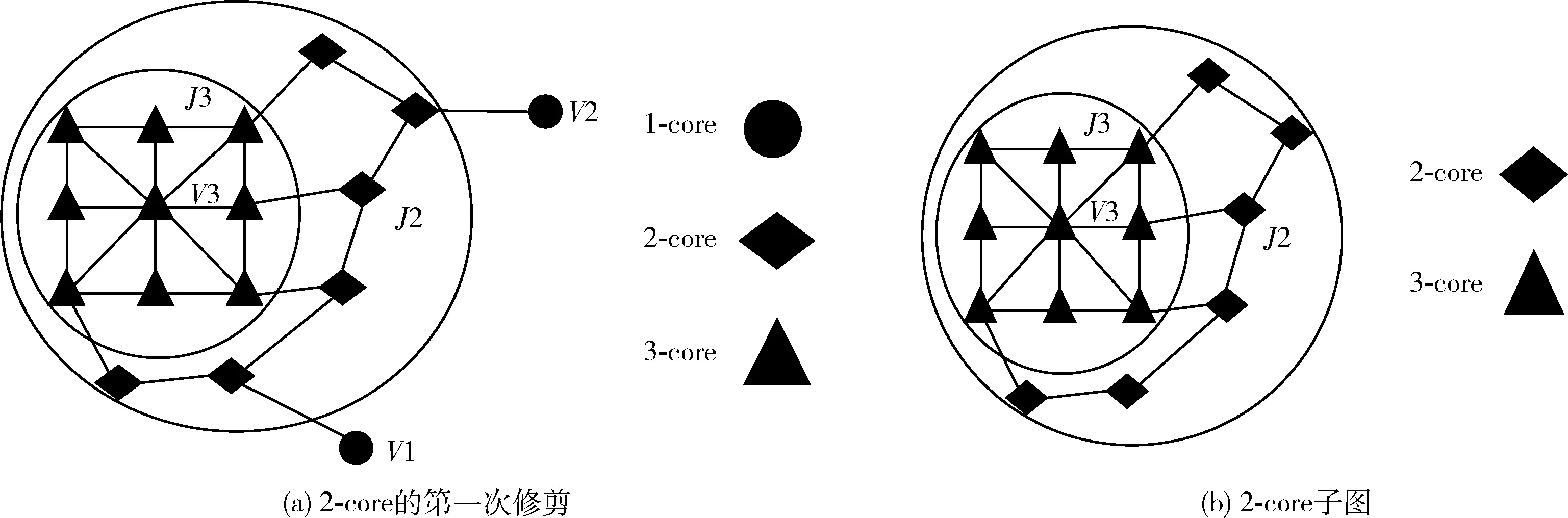
图3 从1-core到2-core的分解过程

尽管k-core表示的概念很明确，每个节点与集合的隶属关系也很清楚，可以很好地将重要性不同的节点划分为不同的网络层，但是k-core分解在捕获节点重要性方面存在一些问题，即其递归修剪过程过于严格，导致一些重要性高的节点没有保留在k-core网络中。由于并非所有概念都适合进行清晰的划分，为了捕获更多的高重要性节点，本文提出基于k-core分解的模糊划分。

模糊k-core分解关于隶属度的模糊函数表示如下

d(v)d=d(v)-d(v)r

(1)

(2)

节点v为图G中任意节点，d(v)表示节点v在完整网络中的度数，d(v)r表示节点v在严格k-core分解过程中将会被删除时的度数，d(v)d表示节点v原始度数与被k-core分解删除时的度数之差，A(v)k为节点v的隶属度，表示其隶属于k-core的概率，其中b=2k。当A(v)k≥0.5时，节点v属于k-core。当k=3时，将节点v保留在k-core子图的条件是d(v)d≥5；当k=5时，节点v保留在k-core子图的条件是d(v)d≥8。与严格的k-core分解修剪条件相比，此模糊函数能保留更多的高重要性节点，k值越大时，效果越明显。并且不会出现隶属度值突增或者突减的情况，保证了不同k值下模糊匹配的平滑性。

若在k-core分解的基础上附加模糊函数，就会对不同粒度层的k-core子图进行重新划分，代表凝聚度分布的核塌缩序列也会相应改变。如图2和图3所示，根据k-core分解的节点分配原则，节点v1和v2属于R1，CCS为 {0，1/2，1/6，3/10}。根据模糊k-core分解的隶属度函数对v1和v2进行二次划分后，节点v1被划分到3-core，属于R3；节点v2被划分到4-core，属于R4，并且其它节点同样也会被隶属度函数进行重新划分，比如节点v3原属于3-core，被二次划分到5-core，属于R5。最终得到图G的模糊子图FKG(V，E)，其CCS为 {0，13/30，1/6，3/10，1/30，1/30}，可以看出，随着模糊k-core分解的加入，CCS也能更详细准确地描述一个图网络的粒度层更丰富的凝聚度分布。

模糊k-core分解的算法过程如下：

算法1：模糊k-core分解

输入：图G(V，E)

输出：模糊k-core子图FKG(V，E)

(1)读取数据集图网络G(V，E)；

(2) 对G(V，E)进行模糊k-core分解；

(3)fori=1tokdo

(4)foreach nodevinVdo

(5)ifd(v)r≥ithen

(6) 保留该节点

(7)else

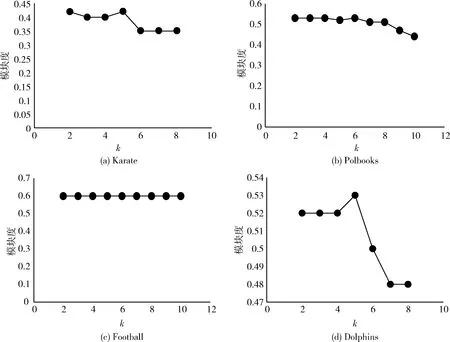
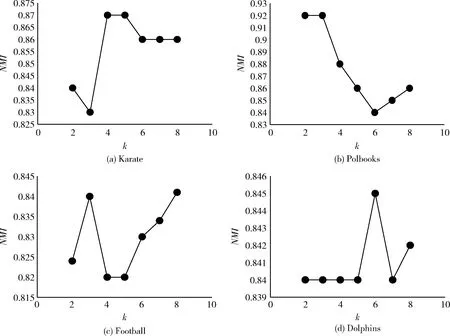
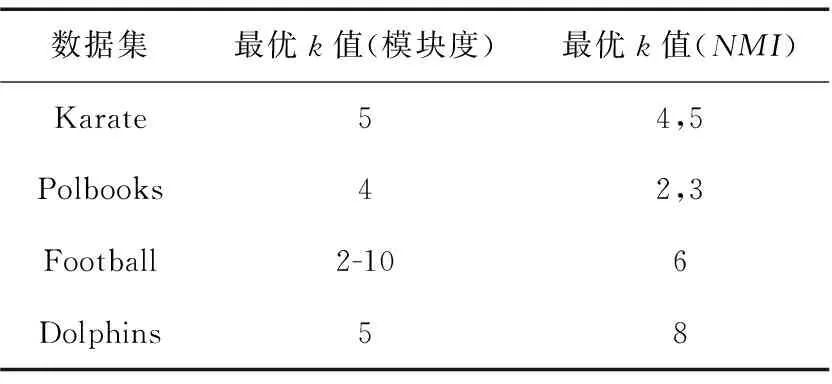
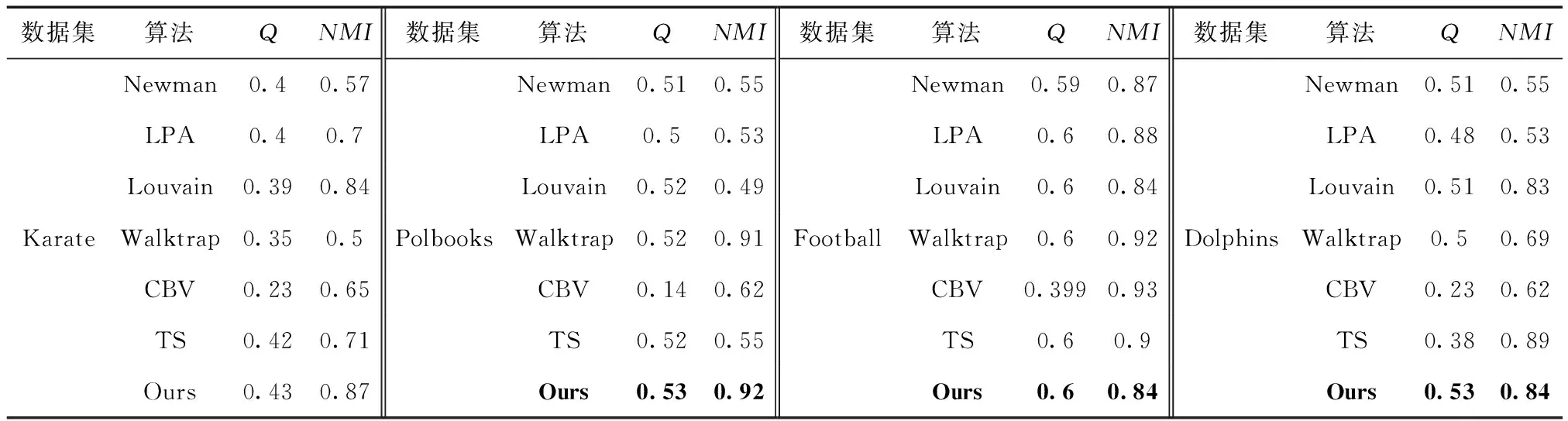
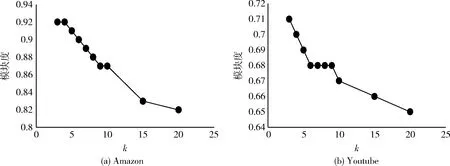
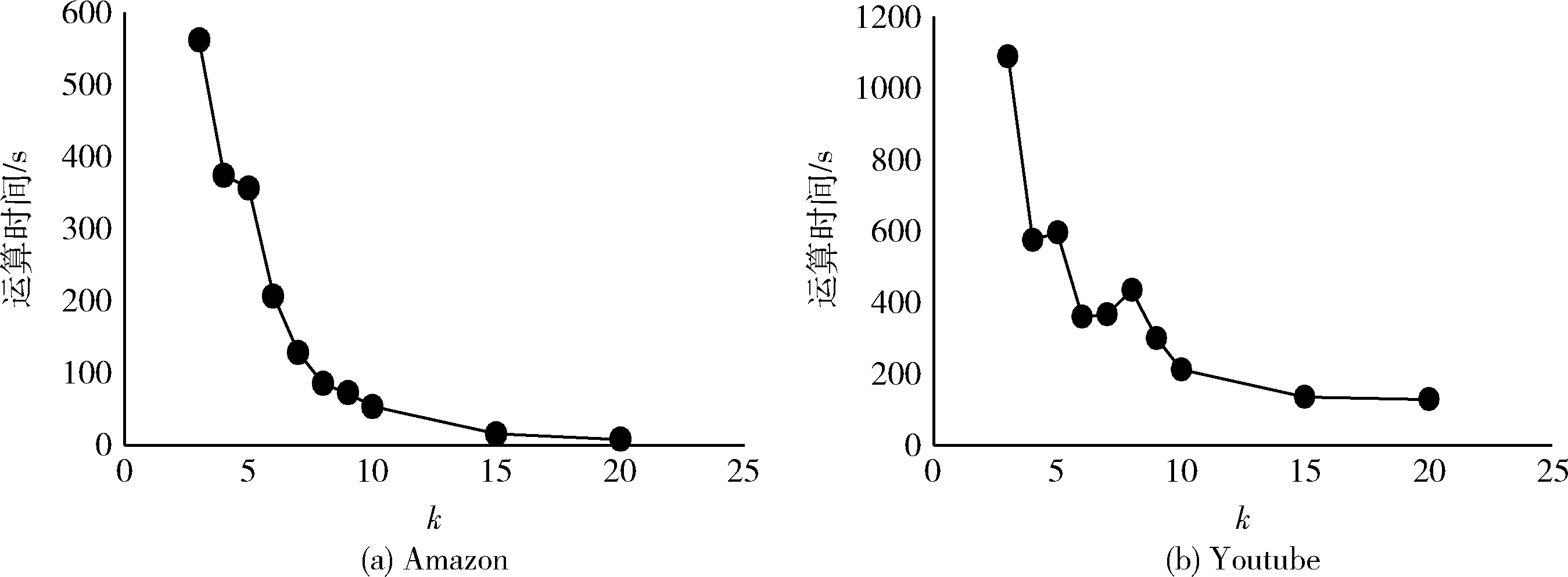
(8)ifd(v)

(9) 删除该节点及其邻边//即该节点A(v)k=0

(10)else

(11)ifd(v)d

(13) 保留该节点

(14)else

(15) 删除该节点及其邻边

(16)else

(17) 保留该节点 //即该节点A(v)k=1

(18)endfor

(19)endfor

2.3 子图社区划分

存在一个图G(V，E)，聚类算法在图中找寻一种节点划分方案，并为每个节点分配一个社区标签，拥有相同标签的节点共同形成一个集群，使得节点集被分割成n个不同的小集群C={C1，C2，C3，C4，……}，其中Cj⊆V且Cj≠∅(i=1，2，3，4，……，n)，满足Ci∩Cj=∅(j=1，2，3，4，……，n且i≠j)，集合C被称为图G的一个社区结构[15]。

模块度Q是一种表示网络社区结构强度的度量值，其取值范围为[-1，1]，常用于衡量一个社区划分结果的优劣[5]。一个理想化的社区划分，是社区内部节点间相似度尽可能的高，同时社区外部节点间的相异度尽可能高，此时模块度的值就越高。也就是说，社区划分的质量越高对应的模块度Q越大[5]

(3)

Ai,j为网络对应邻接矩阵中的一个元素，表示节点i与j之间的边(可能存在，也可能不存在)

(4)

ci和cj分别是节点i和节点j所在的两个社区，如果i和j在一个社区，即δ(ci，cj)则为1，否则为0。m表示网络中所有边的数量，ki表示所有与节点i相连的边的数量(即节点i的度数)

ki=∑j(Ai,j)

(5)

模块度不仅可以用于衡量社区发现的优劣，还可以作为目标函数被优化[16]。

图G的模糊k-core子图FKG(V，E)代表整个图中重要性最高的节点集，对FKG(V，E)进行局部划分后再将标签扩散到整个图网络，可以显著降低运算时间的同时保留或者提升社区划分质量。在本文提出的基于模糊k-core的社区发现算法中，对模糊k-core子图进行聚类的算法过程如下：

算法2：子图社区划分

输入：模糊k-core子图FKG(V，E)

输出：社区结构Cfk={C1，C2，C3，C4，……}

(1) 初始化: 为FKG(V，E)中的每个节点分配社区标签；

(2)do

(3) 计算社区结构的模块度Ql；

(4) 将每个节点划分到其邻接点所在社区，并计算模块度QR

(5) ΔQ=QR-Ql

(6)While(ΔQ>0)do

(7) 保留当前社区结构

(8) 重复步骤(3)

(9)end

(10) 将同一社区节点集简化为单个节点

(11)While(ΔQ>0)

2.4 社区标签扩散

由于模糊k-core子图是整个图网络中重要性最高的节点集，这个节点集能够代表整个图网络的社区结构分布，即其余非模糊k-core子图的所有节点都依附FKG(V，E)并隶属于其社区划分，所以可以根据模糊k-core子图的标签分配结果推断非FKG(V，E)节点的社区标签，从而完善并优化整个图的社区结构。

首先，根据每个无标签节点的带标签邻接点数量，对所有无标签节点进行降序排列。然后，按序列依次遍历每个无标签节点，计算其邻接点集中各标签的占比，为该节点分配占比最高的标签，直到所有节点都被分配到标签为止，完成整个图网络的社区发现。算法过程如下：

算法3：社区标签扩散

输入：FKG(V，E)的社区结构Cfk={Cfk1，Cfk2，Cfk3，Cfk4，…，Cfkn}

输出：全网络社区结构C={C1，C2，C3，C4，……，Cn}

(1)处理非FKG(V，E)节点集Vr；

(2)foreach nodevinVrdo

(3) 计算节点v带标签的邻接点数量

(4)endfor

(5) 对Vr中节点进行降序排列，得到节点序列L

(6)fori=1tondo//n为L中的节点数

(7) 计算节点vi的邻接点集中各标签占比

(8) 为节点vi分配占比最高的标签

(9)endfor

3 实验分析

本节通过在6个社会网络数据集上的实验来验证基于模糊k-core的社区发现算法的有效性。第3.1节为实验准备部分，介绍了实验环境。实验中使用的各类型的数据集，对比算法。模糊k-core分解的重要参数设置以及实验结果评价标准。本文将实验按照使用到的数据集规模大小分为两部分，基于小数据集的实验将在第3.2节中详细介绍，基于大数据集的实验将在第3.3节中详细介绍。

3.1 实验准备

实验的硬件环境为：Intel(R)Core(TM)i7-9700 @3.3 GHZ，RAM:16 GB，软件环境为:Windows 10操作系统，编程语言为:Python。

本文选取了6个在复杂网络领域常用的带基准的真实网络数据集对算法的有效性和准确性进行验证，见表1。这6个数据集都是无方向，无权值网络，其中4个小数据集包括：

Karate网络[17]是Zachary的一个空手道俱乐部的社交网络，由34个节点和78条边组成。节点表示该俱乐部成员，边表示两个节点成员是否在俱乐部之外有联系。

Polbooks网络[18]是美国的政治书籍所构成的网络，由105个节点和105条边组成。节点表示Amazon.com所卖出的美国政治书籍，边表示两本书籍在购买倾向上是相似的。

Football网络[5]是美国职业足球队所构成的网络，由115个节点和115条边组成。节点表示每一个职业足球代表队，边表示两个节点所代表的球队至少进行了一次比赛。

Dolphins网络[19]是一些在一起生活的宽吻海豚所构成的网络，由62个节点和62条边组成。节点代表每一只不同的海豚，边表示两个节点所代表的海豚经常一起活动。

另外还包括两个相对较大的数据集，用于着重验证本文算法在运算时间上的优越性：

Amazon网络[20]是由Amazon在线商城里所出售的商品所构成的网络，由334 863个节点和925 872条边组成。节点表示每一个出售的商品，边表示两个节点所代表的商品经常被一起购买。

Youtube网络[20]是由一个视频分享网站所包含的社交网络，由1 134 890个节点和2 987 624条边组成。节点表示网站中每一个注册用户，边表示两个节点所代表的用户联系紧密。

各数据集的规模见表1。

表1 实验数据集

实验选取了一共6种算法，包括Newman，LPA，louvain，Walktrap等经典算法以及近期的CBV[21]和TS[22]算法，与本文所提出的基于模糊k-core的社区发现算法在相同的4个小数据集上进行实验对比。其中，Newman算法是基于贪心算法的快速社区发现算法，LPA算法是基于节点标签的全局社区发现算法，louvain算法是以模块度优化为目标的全局社区发现算法，Walktrap是基于节点间距离的社区发现算法。

本文实验用于验证算法的指标包括模块度Q，NMI以及运算时间。

由于实验所使用的数据集均是带有基准信息的真实数据集，所以除了模块度，本文也使用NMI[23]表示算法对网络的划分结果与网络的真实划分之间的差异，其取值范围为[0，1]，定义如下

(6)

CA为真实划分的社区数量，CB为算法所得划分的社区数量，Nij表示在算法所划分的社区j中属于真实社区i的节点数量，Ni.表示矩阵Nij的第i行元素之和，而N.j则是第j列元素之和。算法所得划分与真实社区越相近，NMI值就越大，当算法所得划分与真实社区完全一致时，NMI(A，B)等于1。

在本文所提出的基于模糊k-core的社区发现算法中，模糊k-core剪枝过程中k值的取值对于实验结果有着重要影响。算法的核心在于经过模糊k-core修剪后所得到核心子图。模糊k-core子图的规模随着k值的增加而减小，即k值越大，算法所得到的子图就越趋近网络核心，越有利于挖掘出网络的核心节点集，在进行局部社区划分时所需要的运算时间就越少，但在算法的社区标签扩散阶段则需要更多的计算，所以k的取值需要取得一个平衡，使得算法在精确度和运算时间上达到一个最佳平衡，基于此目的，本文提出节点剩余率指标(子图节点数/节点总数)，通过该指标，能够快速的计算出各数据集的最佳k值。

表2列出了当k值取不同的特定值时，各数据集在模糊k-core子图中的节点剩余率，直观地显示各数据集节点度数的分布情况，即相同k值下，节点剩余率越高，网络的平均度数越高，节点间的联系就越紧密。在针对不同数据集进行模糊k-core分解时，该数据集的节点剩余率是一个非常重要的参考数值，能够迅速确定算法最佳k值的具体范围，显著降低最佳k值的计算时间。

3.2 基于小数据集的算法精确性验证

图4、图5展示了本文所提出的基于模糊k-core的社区发现算法分别在Karate，Polbooks，Football和Dolphins这4个数据集上所得到模块度和NMI随着k值不同的变化趋势。表示精确度的模块度和NMI值在不同的数据集上随着k值的增加都有不同程度的变化。结合表2可知，当占比率大于0.6时，模块度值的变化相对很小，并随着占比率的下降平缓降低。而NMI值在变化曲线上则更加复杂一些。综合两个精确度量值，可以得到各数据集的最优k值，见表3。

表2 各数据集在模糊k-core子图中的节点剩余率

图4 小数据集不同k值下的模块度变化

图5 小数据集不同k值下的NMI变化

表3 各数据集最优k值

根据上文所得最优k值，将本文所提出的基于模糊k-core的社区发现算法与Newman，LPA，Louvain，Walktrap，CTS和TS这6个算法在Karate，Polbooks，Football和Dolphins这4个数据集上进行算法精确度对比，对比实验结果见表4。

通过表4中的对比可以看出，本文提出的基于模糊k-core的社区发现算法在4个数据集的对比中综合效果最好，说明本算法在社区划分与聚类的质量上取得了较好的结果。具体表现为，在Karate数据集的对比中，本算法与Louvain算法在NMI值上并列第一，模块度与TS算法并列第一；Polbooks数据集的对比中，算法在NMI值上与Walktrap算法并列第一并远高于其它算法，模块度方面则与大部分算法持平；在Football数据集的对比中，本算法在模块度上和大部分算法持平，但在NMI上稍落后于所对比的算法；而在Dolphins数据集的对比中，本算法在模块度和NMI上都与效果最好的几个算法持平。

表4 小数据集实验对比数据

3.3 基于大数据集的算法效率验证

图6、图7展示了本文所提出的基于模糊k-core的社区发现算法分别在Amazon和Youtube这两个数据集上所得到模块度和所需运算时间随着k值不同的变化趋势。

图6 大数据集不同k值下的模块度变化

图7 大数据集不同k值下的运算时间变化

在Amazon和Youtube这两个数据集上，模块度和运算时间随着k值的增加都有不同程度的下降。随着k值的增加，相对于模块度的缓慢下降，运算时间出现大幅度下降，特别是k值从2到10的变化趋势尤其显著，然后k值从11到20时逐渐缓和。所以对于这两个大规模数据集，为了追求计算效率，设置k=10的值是比较理想的方式。

为了展示本文提出的基于模糊k-core的社区发现算法在运行时间上的优越性，将与GN，LPA和Louvain这3个经典算法在SNAP所提供的Amazon和Youtube两个大规模数据集上进行模块度和运算时间的对比，见表5。

表5 大数据集实验对比

通过表5的对比结果可以看出，由于GN算法和LPA算法分别是自顶向下和自底向上的全局贪心算法，且没有明确的衡量划分好坏的终止指标，所以其时间性能明显较差。Louvain算法在此基础上添加了模块度这一标准，相比GN和LPA，明显提高了算法的划分精度和时间性能。但以上3个算法都针对全网的社区划分，本文所提出的基于模糊k-core的社区发现算法则是以局部社区划分为核心的算法，实验数据表明，本算法在保持算法精度的同时，大幅度减少了运算时间，极大地增加了对大数据集进行社区划分的计算效率。

4 结束语

本文在标准k-core分解算法的修剪规则上融合了基于模糊集理论的隶属度概念，提出了一种以模糊k-core分解为核心的局部社区发现算法。算法提出了一种隶属度方程，通过利用隶属度方程对被k-core分解所删除的节点进行二次判断，最终确定是否将该节点保留在当前粒度层，优化了k-core分解的对节点重要性判断的缺陷，使得更多的高重要节点得以保留在核心节点集。对模糊k-core子网进行局部社区划分后，将划分的社区标签按照邻接点集中的权重占比进行标签扩散，最终完成全局社区发现。与其它社区发现领域的经典算法和近期提出的算法相比可知，本算法在社区发现的精确度和运行时间上都有着更好的表现。但本算法目前没有考虑网络中社区的重叠性，通过识别社区是否重叠，然后将重叠社区分解成为非重叠社区以进一步提高社区发现的精确度是今后研究的主要方向。