基于粒子群优化的变压器绕组热点温度模型研究

李世倩，任 罡，胡晓丽，季 宁，朱向军，秦 雪，刘旻超，姚黎婷，吴旻哲，杨 春，江 兵*

(1.国网江苏省电力有限公司技能培训中心，苏州 215004)(2.南京邮电大学 自动化学院，南京 210023)

绕组热点温度一直是变压器运行时的重要参数，决定变压器使用寿命.据导则GB/T 1094.7-2008规定，温度每超过6 ℃，变压器老化速率就会增加一倍[1-4].

对绕组热点温度获取的方法有：直接测量法、间接计算法.直接测量法是在变压器绕组安装温度传感器，测取温度数据.但变压器内部大电流、强磁场环境会影响传感器性能以及造成腐蚀，造成监测数据不准[5-8].间接计算法是搭建温度模型，根据变压器运行参数间接计算绕组热点温度[9-11].其中国标推荐计算公式以及文献[12]采用的热阻模型，只将变压器视作线性系统，粗略估算绕组温度动态变化过程；文献[13]提出一种根据顶层油温计算绕组热点温度热电类比模型，但该算法综合考虑因素较少，计算效果不佳；文献[14]提出一种结合变压器绕组平均温度以及散热器表面温度计算绕组热点温度算法模型，该方法能近似计算绕组热点温度.

文中将顶层油温对对流换热系数进行建模，对绕组传热分析，构建基于顶层油温计算绕组热点温度的算法模型.综合考虑所构建模型存在系统误差，以及变压器顶层油温和热点区域油温存在温差，添加修正因子，并用粒子群算法进行参数寻优，优化算法模型.分析不同负载率下修正因子变化情况，并用最小二乘法将负载率和修正因子构建函数关系.实验表明，该算法能很好地计算热点温度，且优于文献[14]算法，整体误差小，有更好的适用性.

1 热源分析

油浸式变压器在运行过程中，温升主要来源是绕组和铁芯产生的损耗.假设变压器在运行过程中，绕组的负载损耗和铁芯的空载损耗呈均匀分布，可以根据传统经验公式来求得各损耗值.

1.1 负载损耗

负载损耗主要是指运行过程中绕组通电时产生的电阻损耗也就是铜损，绕组的铜损为[15]：

P=I2·Rcu

(1)

式中：I为通过绕组的电流，A；Rcu为绕组的电阻值，Ω.

1.2 空载损耗

空载损耗主要是铁芯产生的励磁损耗，公式为：

Pfe=δhfBm2+δef2Bm2

(2)

式中：δh为磁滞损耗系数；δe为涡流损耗系数；f为电流频率Hz；Bm为磁通密度最大值，Wb·m-2.

在实际工程计算中，变压器的空载损耗往往是根据最大磁通密度Bm，选用硅钢片的材料，再查询变压器生产手册来确定铁芯单位质量的铁损，之后再乘以铁芯总质量得到最终的空载损耗[6]：

P0=Kp0·GFe·pt

(3)

式中：Kp0为空载损耗附加系数；GFe为铁芯的总质量，kg；pt为铁芯的单位质量空载损耗，W·kg-1.

2 热点温度建模

2.1 物理模型建立

根据变压器各种损耗、油性质以及外部环境参数，利用ANSYS仿真软件建立变压器模型，如图1.

图1 变压器模型

变压器建模参数如表1，油视作理想流体；变压器冷却方式为自冷，进口流速设定为0.5 m·s-1，外部环境温度设定为300 K.经有限元仿真后，可获得对流换热系数、油温、热点温度等数据.

表1 绕组和铁芯材料属性表

2.2 热点温度算法

运动的流体和接触的固体表面之间由于存在温度差而发生热量传递，被称作对流传热.根据牛顿冷却定律可以得到对流传热为[17]：

Q=hA(Ts-Tf)

(4)

式中：Q为换热量，J·s;h为对流换热系数，W·(m2·K)-1；A为固体和流体接触的换热面积，m2；Ts为固体温度，K;Tf为接触面处流体温度，K.

其中对流换热系数为[18-19]：

(5)

(6)

(7)

式中：Nu为努塞尔系数；kf为流体的导热系数；l为特征长度；C、n为根据经验表确定的常数；g为重力加速度；β为体积膨胀系数；ΔT为流体和固体之间的温差；v1为流体的运动速度；δ为运动粘度；cp为油的比热；σ为油的密度；Gr为格拉晓夫数；Pr为布朗特数.

以上分析知，热点区域油温是对流换热系数的重要影响因素.鉴于实际应用中对流换热系数无法直接获取，且热点区域油温不易获得，故将对流换热系数数据以顶层油温为变量，采用Gaussion曲线逼近的方法构造函数关系：

h=f(Toil)

(8)

综合式(4，8)，绕组热点温度的算法模型为：

(9)

式中：Toil为顶层油温，K；Toil*为热点区域油温，K.由于油箱顶层油温与热点区域油温存在温差，以及用式(8)计算的h存在系统误差，对式(9)添加修正因子k1、k2，构建基于顶层油温计算热点温度的算法模型：

(10)

3 基于粒子群算法的热点温度模型优化

3.1 粒子群算法原理

粒子群算法具备很好地全局寻优能力，从随机解出发，通过迭代寻找最优解.粒子群中的粒子运动一次，其位置发生相应的改变，经粒子群运算后得到新的个体极值pbest和群体极值gbest.假设在一个D维的目标搜索空间中，有N个粒子组成一个群落，其中第i个粒子表示为一个D维的向量[20-22]：

Xi=(xi1,xi2,xi3...,xiD)i=1,2,3....,N

(11)

第i个粒子的运动速度也是一个D维的向量：

Vi=(vi1,vi2,vi3...,viD)i=1,2,3....,N

(12)

第i个粒子搜索到的最优个体极值pbest为：

pbest=(pi1,pi2,pi3...,piD)i=1,2,3....,N

(13)

整个粒子群搜索到的最优群体极值gbest为：

gbest=(pg1,pg2,pg3...,pgD)

(14)

在找到这两个最优值时，粒子群根据如下位置更新自己的速度vid和位置xid：

(15)

式中：c1、c2为学习因子；r1、r2为均匀随机数；w为惯性权重.

3.2 粒子群算法寻优过程

文中以式(10)作为目标函数，将每个搜索空间中的潜在解k1、k2视作粒子，用粒子群算法(图2)寻找最优k1、k2值，具体过程如下：

图2 粒子群算法流程图

(1)初始化粒子群，包括种群规模N、每个粒子的位置xi和速度vi.

(2)计算每个粒子的适应度值Fit[i].

(3)比较每个粒子的适应度值Fit[i]和个体极值pbest(i)，如果Fit[i]>pbest(i)，则用Fit[i]代替pbest(i).

(4)比较每个粒子的适应度值Fit[i]和全局极值gbest，如果Fit[i]>pbest(i)，则用Fit[i]代替gbest.

(5)更新粒子的速度vi和位置xi.

(6)满足条件时(误差足够好或达到最大迭代次数)则退出，否则返回(2).

4 实验验证与结果分析

4.1 基于顶层油温算法分析

采用0.7倍负载率工况下对流换热系数和顶层油温构造函数关系,负载率指变压器实际功率与额定功率之比，如图3.

图3 对流换热系数和油温关系

采用Gaussion曲线逼近的方法，函数表达式为：

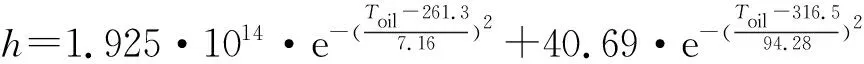
(16)

综合分析变压器运行时不同负载率工况下的对流换热系数曲线，将负载率η分别设置为0.2、0.5、0.7，得到3种工况下顶层油温和换热系数曲线，如图4.

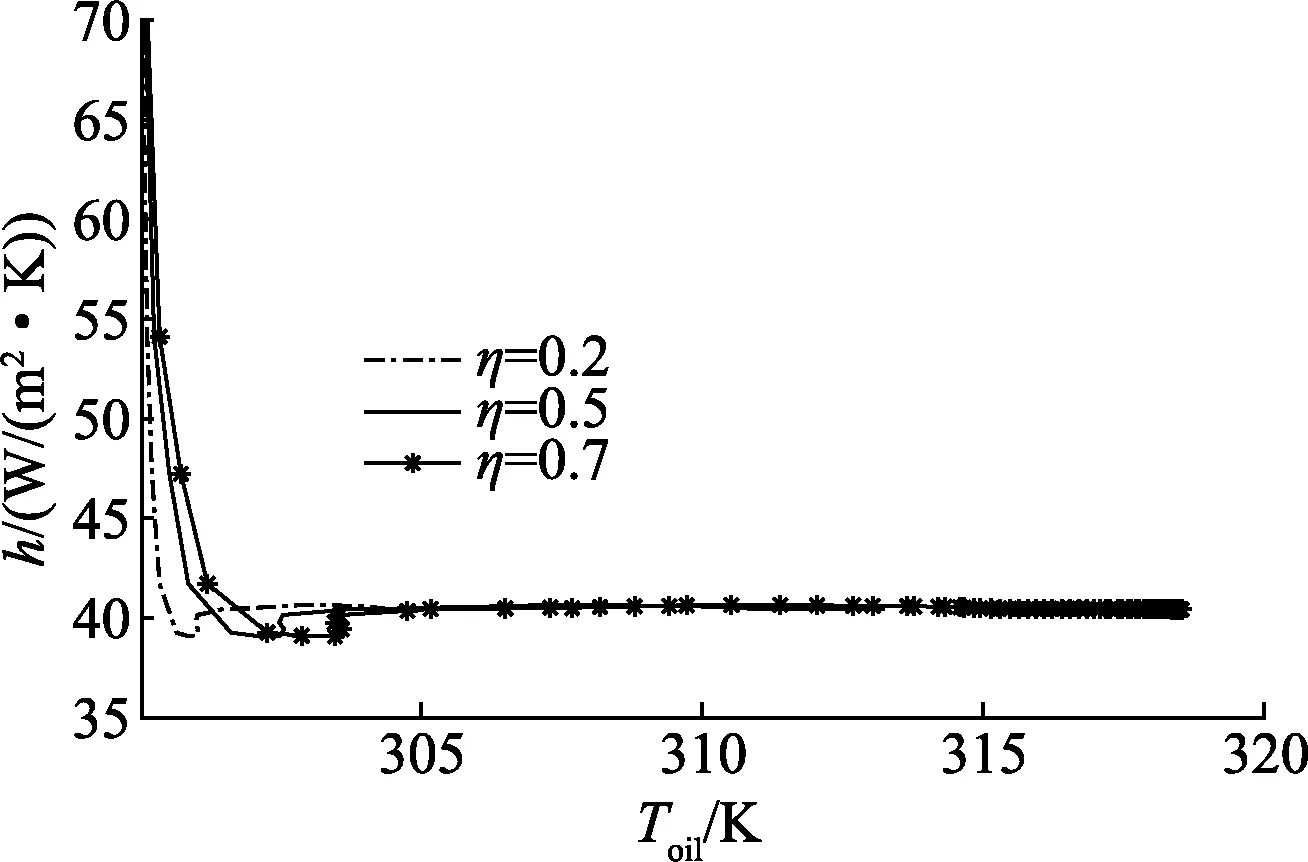
图4 不同负载率下对流换热系数曲线

图4表示，不同负载率下顶层油温-对流换热系数曲线存在差异，所以需综合分析不同负载率工况下的修正因子.考虑曲线变化趋势基本一致，将对流换热系数和顶层油温所构建的函数关系设定为式(16)，并利用粒子群算法对式(10)进行参数寻优.

4.2 粒子群算法参数寻优结果

文中用Matlab软件进行仿真，粒子群算法的参数设置如下：粒子群规模为50；最大迭代次数为500；粒子最大移动速度为10；学习因子c1、c2均设置为2；r1、r2设置为[0，1]范围均匀随机数；惯性权重的范围为[0.4,0.9]，以残差平方和作为适应度函数，进行粒子群算法寻优结果如图5，6.

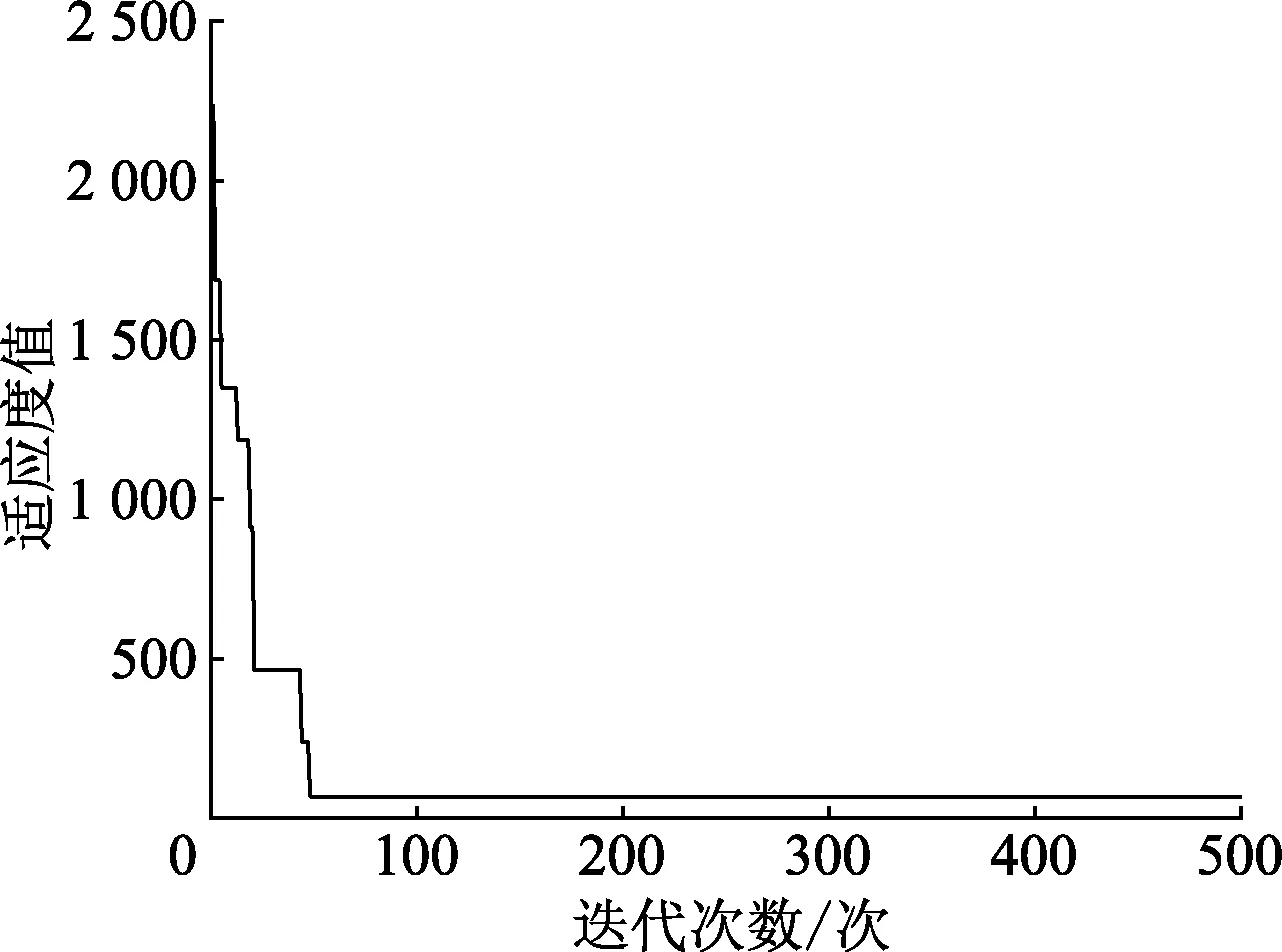
图5 粒子群算法迭代次数

由图5知，算法在迭代次数达到60次时，就会收敛且变得相对平稳.由图6知，由粒子群算法优化后的热点温度算法模型温度值与实际值较为贴合，此时残差平方和RSS=65.518 5,对应的最优参数：k1=0.956 4,k2=1.024 5.用同样方法得到不同负载率工况下修正因子，如表2.

图6 粒子群算法寻优效果

表2 不同负载率下的修正因子

由图7和图8知，修正因子k1、k2会随着负载率的变化而变化，将两个修正因子采用最小二乘法分别与负载率构造函数关系，即可得到不同负载率下对应修正因子的数值，函数表达式如下：

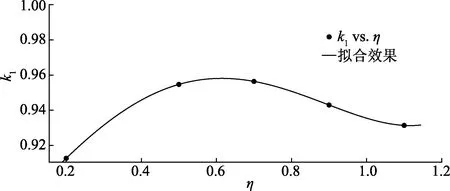
图7 修正因子k1与负载率关系

图8 修正因子k2与负载率关系

k1=0.273 3η4-0.522 6η3+

0.094 2η2+0.222 4η+0.868 2

(17)

k2=0.006 5η2+0.027η+1.003

(18)

4.3 实验结果分析

根据变压器模型，在额定功率下，将负载率设定为1，根据式(17，18)所对应的修正因子k1=0.935 5，k2=1.036 5.根据式(10)在负载率η为1时热点温度数据如图9，误差如图10.

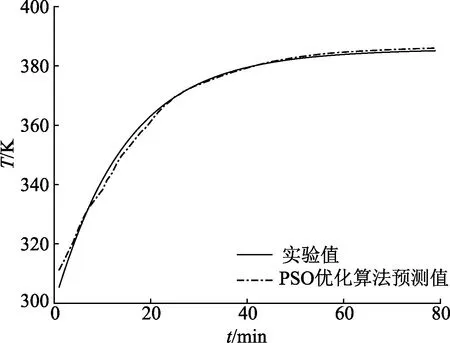
图9 基于PSO优化的热点温度算法曲线

图10 基于PSO优化的热点温度算法绝对误差

由图9知，基于PSO优化的热点温度算法温度数值贴近实验数据，且数据变化趋势保持一致.由图10知，在整个温升的过程中绝对误差最大值为5.8 K,热点温度稳定时，误差保持在1 K以下.

文献[14]提出的热点温度算法为：

(19)

式中：H为热点系数，文中为1.1；Tave为绕组的平均温度K；Trt、Trb分别为散热器表面的顶部温度和底部温度K；文中模型为自冷方式，环境温度为300 K，式(19)可以转换成：

Thot=Toil+H(Tave-Toil)

(20)

根据式(20)计算额定功率下绕组热点温度，其温升曲线如图11，绝对误差曲线如图12.

图11 文献[14]算法温升曲线

图12 文献[14]算法绝对误差曲线

由图11知，算法结果与实验温度数据变化趋势基本一致，但是该算法所得温度数据大于实验数据.由图12知，随着温度上升误差也会不断增加，热点温度稳定时绝对误差在2.8 K左右.

将两种算法进行对比由图9和11知，两种算法都能很好地计算热点温度，反映温度变化趋势，但文中算法经PSO优化后，结果更加贴近实验数据；另由图10和12知，两种算法误差均较小，但基于PSO优化的热点温度算法整体误差小于文献[14]算法.当热点温度趋于稳定状态时，绝对误差小于1 K，模型适用性更好.

5 结论

(1)提出一种基于PSO优化的变压器绕组热点温度算法，通过分析顶层油温是对流换热系数的重要影响因素，将二者构造函数模型.结合绕组传热分析，构建基于顶层油温计算绕组热点温度的算法模型.

(2)分析算法模型存在的系统误差以及顶层油温和热点区域油温温差关系，对算法模型添加修正因子，并利用粒子群算法进行参数寻优.还进一步分析不同负载率下修正因子的差异，利用最小二乘法将二者构造函数关系，得到不同负载率下的修正因子.

(3)通过实验对算法分析验证，并同文献[14]所提算法做对比.结果表明，文中算法下热点温度数据与实验数据更为贴近，当热点温度趋于稳定状态时，绝对误差小于1 K.算法整体误差较小，适用性更好.