仿荷叶脉络薄壁管耐撞性能研究

王勇辉, 何 强, 顾 航

(江苏科技大学 机械工程学院，镇江 212100)

薄壁结构质量轻且具有良好的能量吸收特性，广泛应用于车辆、航空和船舶等领域.金属薄壁结构一直以来都是学者们研究的热点.在十几年以前，学者们就对薄壁结构做了相关的工作，通过数值、分析和实验的方法，对不同截面(如：方形[1]、圆形[2]、六边形[3])的薄壁结构进行了研究.

为进一步提高薄壁结构的力学特性和能量吸收效率，学者们做了大量的研究.文献[4]基于实验法，研究了3种不同管壁厚度、两种跨径的泡沫铝合金填充圆管三点弯曲力学性能，获得了泡沫铝合金填充管承载过程中的3种变形模式.文献[5]研究了紧致比相同但中径和厚度不同的薄壁圆管在轴向冲击载荷作用下的动态响应特性.文献[6]采用解析和数值方法研究了几种简单截面薄壁梁在横向冲击作用下的弯曲性能，结果表明b型截面梁力学性能优于原简支截面梁.文献[7]进一步开展波纹管的加工试验，研究表明波纹管比传统管具有更低、更稳定的压溃力.文献[8]提出了一种混合波纹管，并通过研究发现薄壁板波长和恒定波纹比对其耐撞性有着显著影响.

以上研究所提及的薄壁结构，其横截面结构简单，但却具有较好的耐撞性能.近年来，为设计出具有更加优异的耐撞性能的薄壁结构，越来越多的研究以自然界生物结构为原型，将生物结构特征引入到薄壁管的设计中，进而有效提高薄壁管的耐撞性[9-16].荷茎类比于多胞薄壁管，孔道的分布使荷茎受力稳定，不易弯曲变形.荷叶叶脉在生物结构上不仅承担养分输送的功能，还支撑着整个叶片的重量和外部载荷，保证叶片的整体刚度和平面延性.因此，叶脉分布的合理性和大小对叶片的承载力和保持叶片的形状起着决定性的作用.然而，还没有相关的研究将这种生物结构特征引入到薄壁结构的设计中.

文中选择荷叶脉络为生物原型(图1)，设计出一种具有叶脉分支特征的仿生薄壁结构(BTS)，可运用于车辆、航空和船舶等领域的安全防护.基于ABAQUS对其进行三点弯曲数值仿真，进一步分析BTS内外圆直径之比(γ)、主干数目(N)、冲击速度(V)以及壁厚(T)对其耐撞性能的影响，最后对其进行了截面变厚度优化设计.

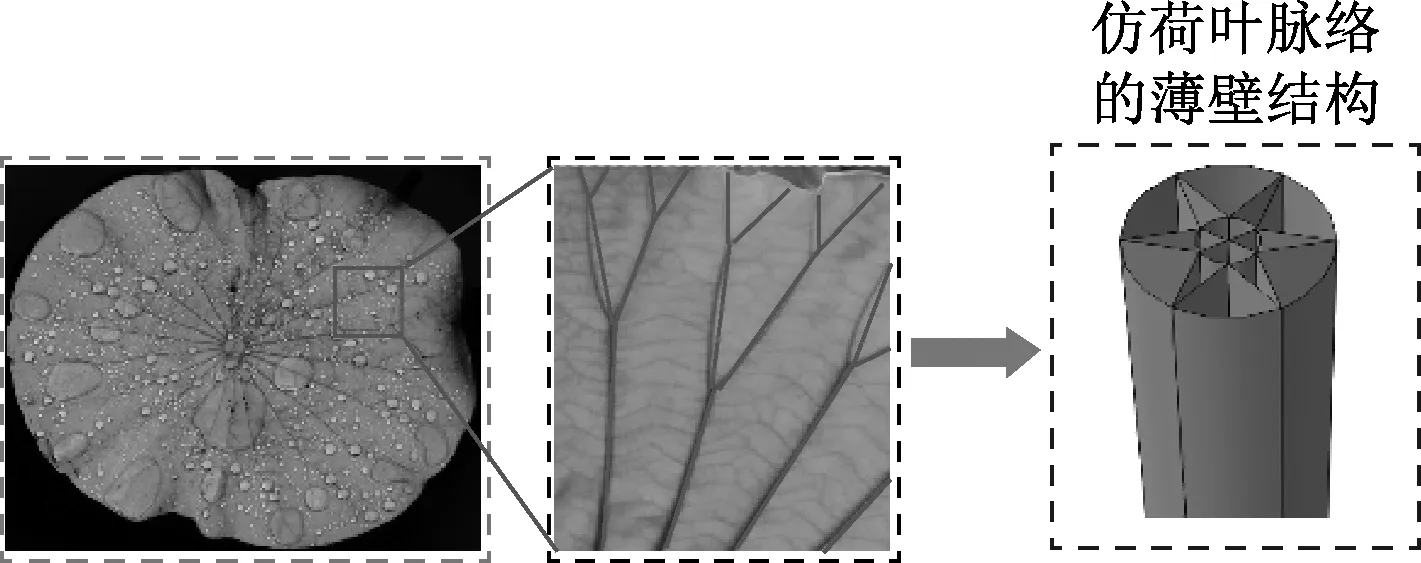
图1 仿荷叶脉络薄壁结构的几何构性

1 BTS的结构设计

图2分别为BTS的三点弯曲几何模型和横截面，在BTS中心处受到垂直向下载荷的冲击.如图2(a)，BTS对称放置在两个支座上，压头位于其中心位置上方.其中，两支座和压头的直径为50 mm，两支座中心的距离为420 mm，压头冲击BTS的速度为4.4 m/s.在图2(b)中，Φouter为BTS的外圆直径，Φinner为BTS的内圆直径，T为壁厚，N为主干数目.定义BTS的结构参数γ为Φinner和Φouter的比值，BTS的总长为550 mm，壁厚T为1 mm，外圆直径Φouter等于60 mm，内圆直径Φinner随着结构参数γ的变化而变化，图3为BTS的截面演变.

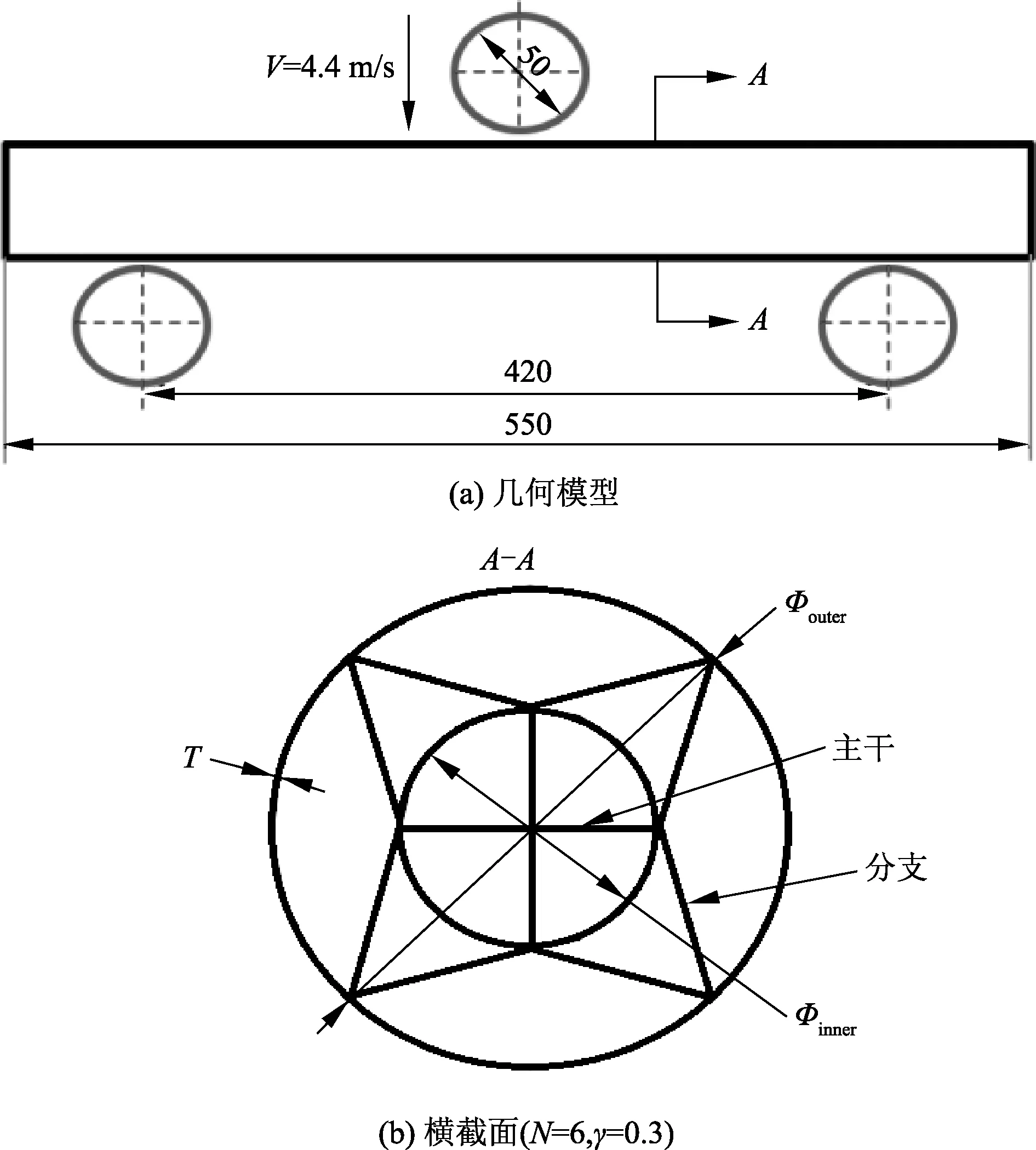
图2 BTS三点弯曲几何模型和横截面

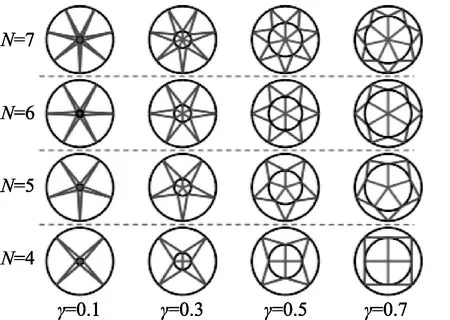
图3 BTS的截面演变

2 有限元模型的建立

基于非线性动力学软件ABAQUS对BTS进行有限元建模.建模过程中，采用动力显示分析步，管壁采用壳单元建模，支座和压头设置为刚体.在压缩过程中的接触设置：管件和压头、支座之间的接触设为面面接触，管件自身的接触为单面接触，各结构之间的静、动摩擦系数设置为0.3和0.2[9-10].采用沙漏刚度用来控制沙漏变形的能量，缩减积分用来避免体积自锁，不考虑铝合金材料的失效.图4为BTS的有限元模型，在权衡模型计算精度和运算成本后，网格尺寸设置为2.5 mm×2.5 mm.

图4 一种BTS在横向冲击下的有限元模型变

BTS的材料为AA6061-T4型号的铝材，其材料参数为密度ρ=2.7×103kg/m，弹性模量E=68.2 GPa，泊松比ν=0.3，屈服应力σ=116 MPa.在有限元建模过程中，BTS的材料采用AA6061-T4的应力-应变函数，材料的应力-应变曲线图，如图5.由于铝对应变率不敏感，在仿真分析中材料应变率效应可以忽略不计.

图5 AA6061-T4应力-应变曲线

3 有限元模型的验证

在参考文献[17]三点弯曲实验中，直径为50 mm的圆柱压头以4.4 m/s的速度在跨中冲击空心圆管.为验证该模型的可靠性，采用与参考文献[17]中相同的结构参数、截面属性和工况.如图6、7，将有限元模型仿真的结果和实验结果对比，发现仿真计算结果与实验结果、仿真变形模式与实验变形模式吻合较好.由此可知，该有限元建模方法可以用来建立BTS的有限元模型.

图6 空心圆管的变形模式

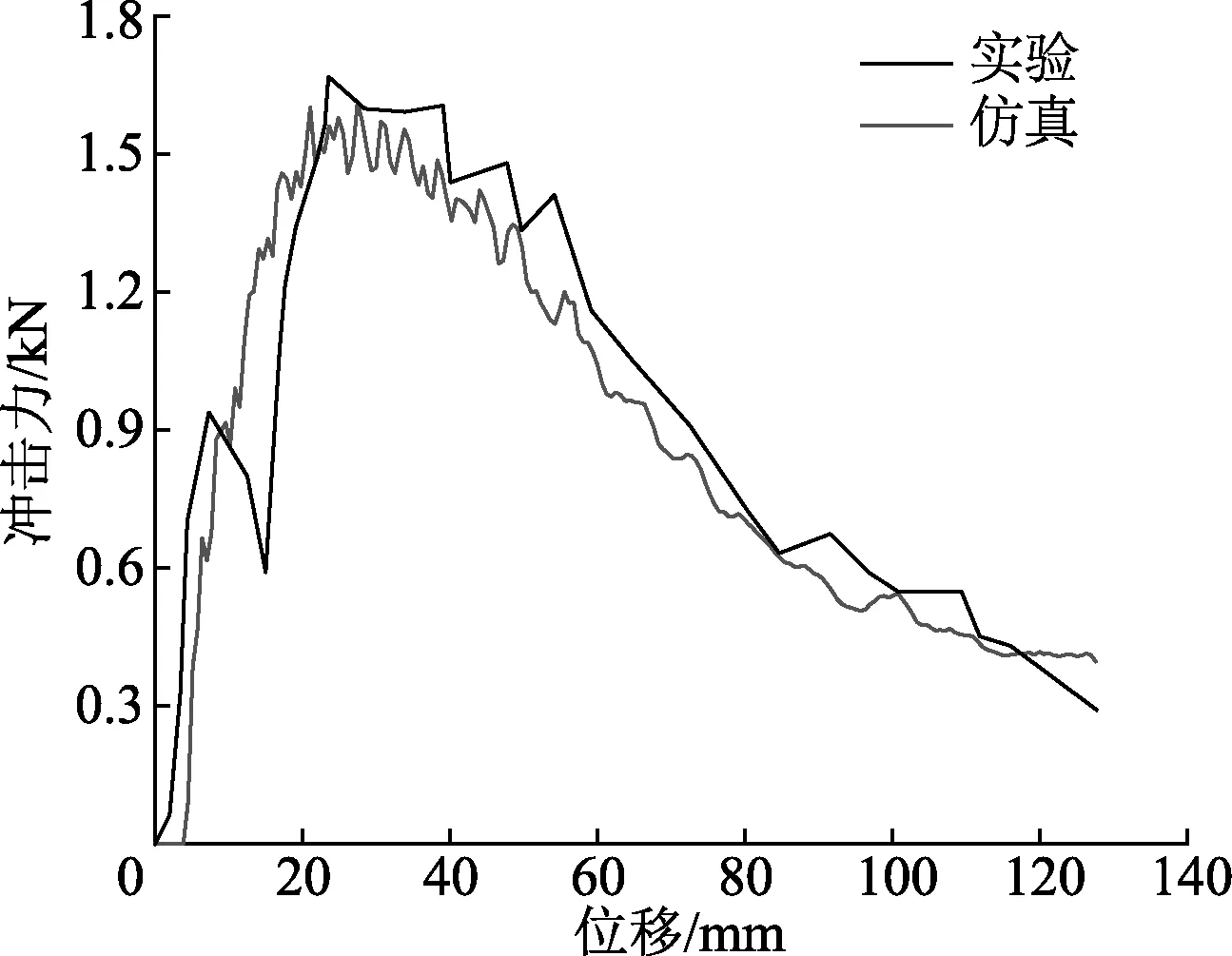
图7 实验、仿真的力与位移曲线对比

4 BTS耐撞性能的分析

4.1 评价指标

为了研究BTS的耐撞性，定义耐撞性指标是非常重要的.通常吸能量(EA)，平均压溃力(MCF),最大碰撞力(MIF)，比吸能(SEA),压溃力效率(CLE)是常用的指标.其中，比吸能(SEA)被广泛用来评价结构的吸能性能，SEA越大，结构的吸能性能就越好，计算公式为：

(1)

式中：M为结构总质量，EA为结构能量吸收总量.EA的计算公式如下：

(2)

式中：S为冲击端压头加载位移；F(x)为瞬时碰撞力.

压溃力效率是用来评价碰撞载荷的均匀与一致性的指标，计算公式为：

(3)

式中：MCF为平均压溃力；MIF为最大冲击力；MCF的计算公式为：

(4)

4.2 BTS与传统圆管对比分析

表1为等质量的BTS和圆管耐撞性指标之间的对比，从表中可以看到，BTS的比吸能1.03 kJ较圆管的比吸能0.97 kJ多6.19%，表明BTS的吸能特性要优于圆管；在最大碰撞力方面，BTS的最大碰撞力6.04 kN比圆管的最大碰撞力5.63 kN高7.24%；在碰撞效率方面，BTS和圆管相差不大，变形加载都比较均匀.BTS和圆管的详细参数如表2.

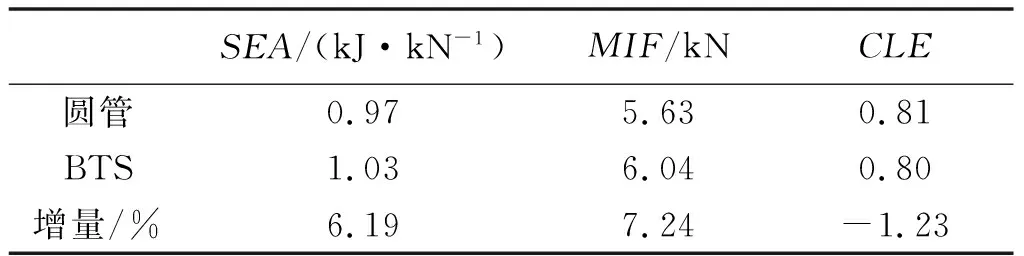
表1 耐撞性指标对比

表2 结构参数

为了进一步了解BTS与传统圆管吸能特性的差异，对其变形模式进行研究.图8为BTS和圆管的变形模式，图中变形特征有弯曲和局部凹陷.局部凹陷有两种形式，分别是内凹皱褶和外凸皱褶，内凹皱褶的有效接触面积和外凸的数量是决定结构吸能特性的重要因素.图8(a)中，在圆管的局部凹陷位置有1个内凹皱褶和2个外凸皱褶，圆管凹陷位置与其他位置之间过度均匀，变形后过度区域光滑.但内凹皱褶的有效接触面积较小，导致变形区域集中，使得承受的弯曲载荷不能向管的两端传递.最后，圆管中心位置的截面被压扁.

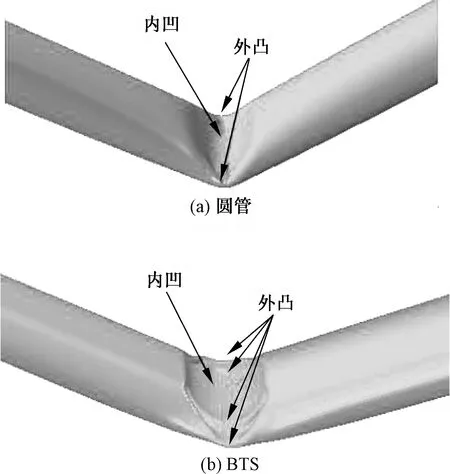
图8 BTS和圆管的变形模式

图8(b)中，在BTS的局部凹陷位置有1个内凹皱褶和4个外凸皱褶，内凹皱褶有较大的有效接触面积.而较大的内凹皱褶有效接触面积能很好的吸收冲击过程中产生的能量，较多的外凸皱褶数目能有效地分散弯曲载荷.说明BTS能够有效地向两端传递弯曲载荷，避免了变形区域集中，从而具有较好地吸能特性和抗弯性能.

4.3 冲击速度的影响

冲击速度对薄壁结构的耐撞性有着重要影响，因此探究不同冲击速度对BTS变形模式和吸能特性的影响是非常有意义的.根据实际的碰撞速度，研究4、8、12、16、20 m/s的冲击速度下BTS的动态响应,选择结构参数为γ=0.3，N=6，T=1的BTS.图9为不同冲击速度下BTS的力与位移曲线和SEA值.从图9(a)中可以看到，不同冲击速度下BTS的力与位移曲线呈现相同的趋势.碰撞开始时，碰撞力急剧增大至峰值，接着迅速下降，随后趋于稳定，最后碰撞力逐渐下降.从不同冲击速度下BTS的SEA值(图9(b))可以看到，随着冲击速度的增加，SEA值相差不大.

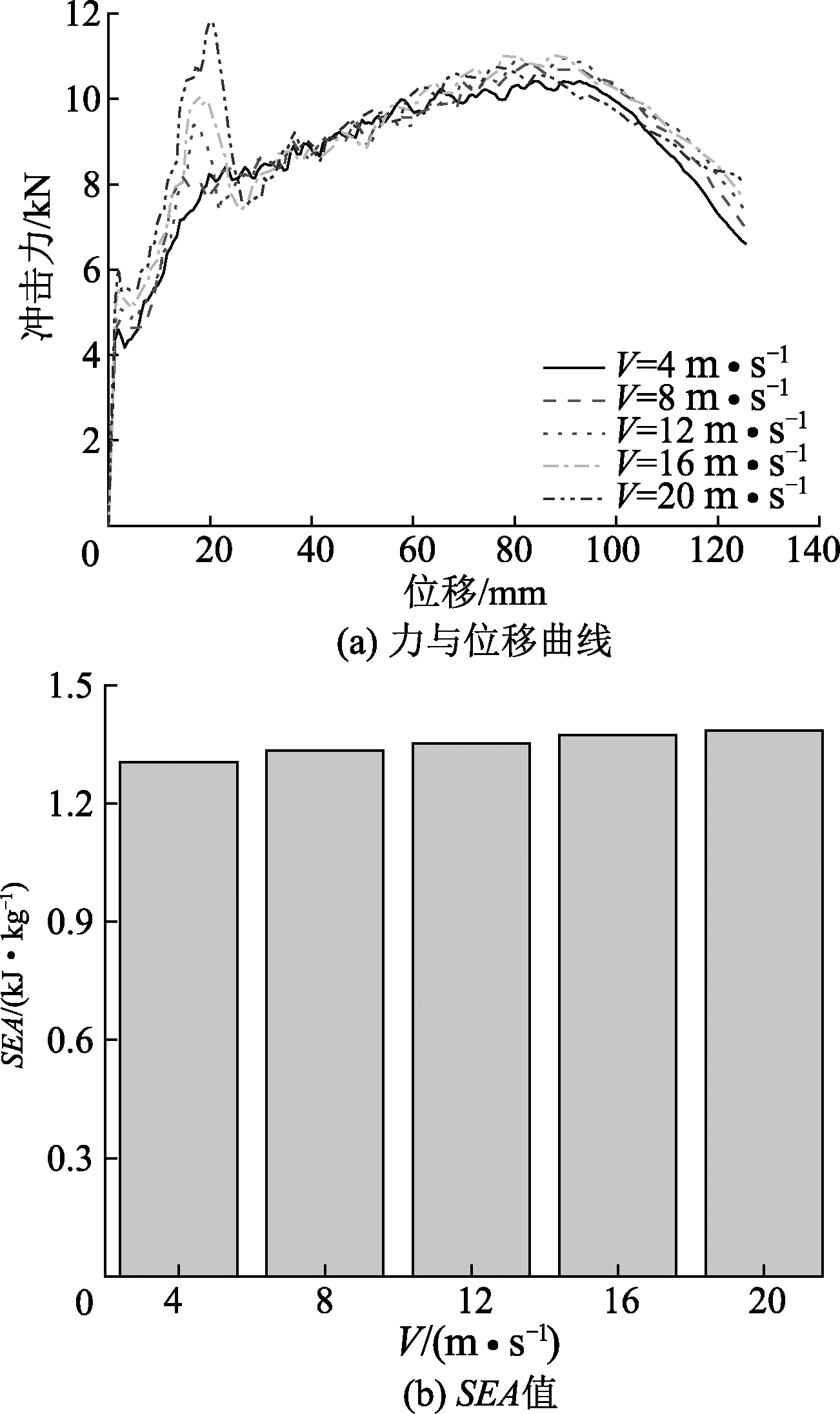
图9 不同冲击速度下BTS的力与位移曲线和SEA值

图10为不同冲击速度下BTS的变形模式，可以看出，随着冲击速度的增大，BTS的变形模式没有显著的差异.说明加载位移大于90 mm时，BTS的承载性能逐渐丧失，并且碰撞峰值力随加载速度的增加而增加；冲击速度增大对BTS的变形模式没有明显的影响.

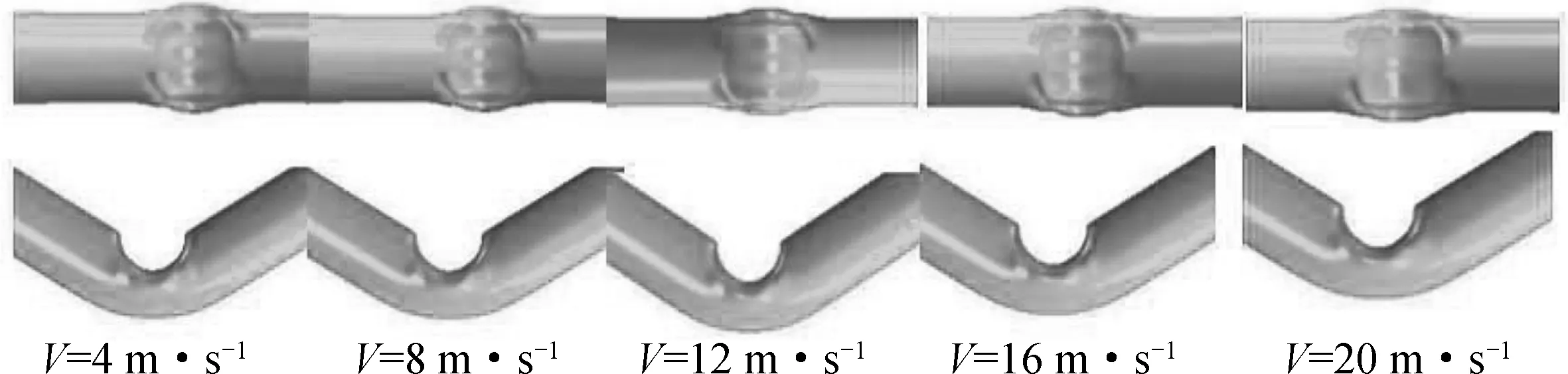
图10 不同冲击速度下BTS的变形模式

4.4 比值γ的影响

为了研究BTS内外圆直径之比(γ)的影响，设计了7种不同的γ值：0.1，0.2，0.3，0.4，0.5，0.6，0.7.需要注意的是，γ必须控制在一定的范围内，防止分支发生交叉重叠.图11为不同比值γ下BTS的SEA、MIF、CLE值.从图中可以看到，随着γ值的变化，SEA和MIF呈现相同的趋势：γ≤0.6时，随着γ值的增加而逐渐增加；当γ=0.7时，SEA有下降趋势.对于CLE而言，随着γ值的增加变化不大.说明比值γ对BTS的耐撞性有着重要影响，适当增加γ值可以有效提高BTS的吸能特性，但同时会增加碰撞峰值力.

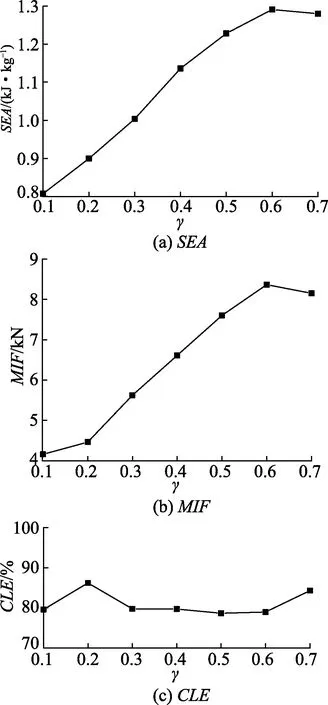
图11 不同比值γ下BTS的SEA、MIF、CLE值

4.5 主干数目N的影响

为了研究主干数目(N)的影响，设计了4种不同的N值：4，5，6，7.图12为不同主干数目N下BTS的SEA、MIF、CLE值，可以看出，SEA和MIF都随着N的增加而增加.特别N>6时，SEA的增长率大于MIF的增长率.就CLE而言，N<6时，随着N的变化，CLE值变化不大；N=7时有着最大的CLE值.说明主干数目(N)对BTS的耐撞性有着重要影响，通过增加主干数目，可以有效提高BTS的吸能特性；当N>6时，增大N值对提高BTS的耐撞性有着更好的增益效果.

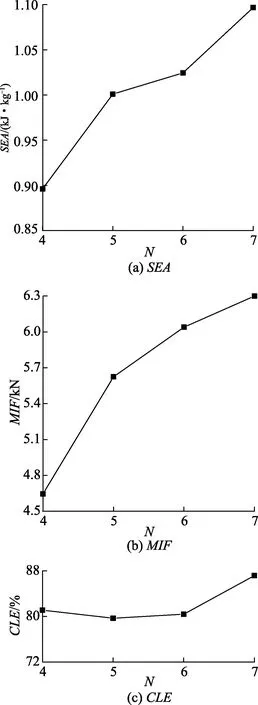
图12 不同主干数目N下BTS的SEA、MIF、CLE

4.6 壁厚T的影响

为了研究壁厚T的影响，设计了5种不同的T值：1,1.5,2,2.5,3 mm.图13为不同壁厚T下BTS的SEA、MIF、CLE值，由图可知，SEA随壁厚T的增大，先增大后逐渐稳定；MIF随着N的增大而增大；随着N的变化，CLE变化不大.特别地,T≤2mm时，SEA的增长率大于MIF的增长率.说明T≤2 mm时，增大壁厚对于提高BTS的耐撞性有着更好的增益效果.

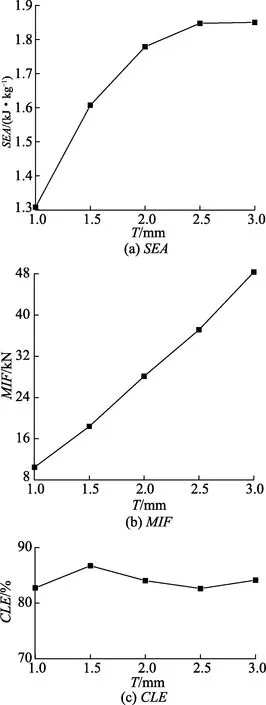
图13 不同壁厚T下BTS的SEA、MIF、CLE

5 截面变厚度优化设计

综上研究表明，冲击速度、比值γ、主干数目N、壁厚T对BTS的耐撞性能有着重要影响.其中，BTS的壁厚对其能量吸收效率的影响最大.因此，为了得到能量吸收效率最优的BTS，最直接有效的方法就是对其进行截面变厚度优化设计.采用响应面法，以壁厚T和MIF为约束条件，SEA为优化目标对BTS进行截面变厚度优化设计.根据前面BTS的结构参数影响分析，BTS的比值γ取0.6，主干数目N取7，壁厚T的范围设为0～2 mm.图14为BTS的横截面，从图中可以看到优化的设计变量有T1、T2、T3：T1为内外圆的壁厚，T2为分支的壁厚，T3为主干的壁厚.

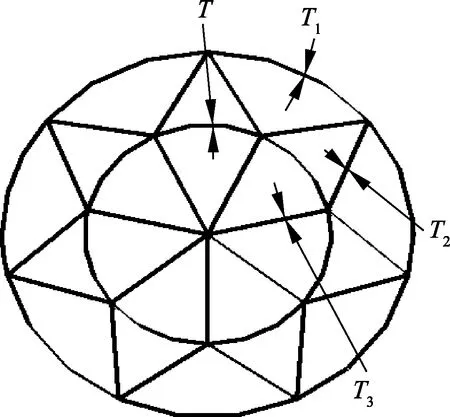
图14 BTS的横截面

图15是响应面法的优化设计流程.首先，确定BTS的优化问题；然后，根据其优化问题进行实验设计，获得相应的设计样本点，并通过有限元仿真得到相应的目标函数值.最后，基于设计样本点及其响应值，通过回归分析建立响应面模型，并且对响应面模型求最优解.对获得的最优解进行检验，如果预测模型得到的最优解与数值模拟的值误差在允许范围内，则最优解可信度高.如果它们之间的误差较大，则需要调整设计域，对其重新进行优化分析，直至误差在允许范围内.

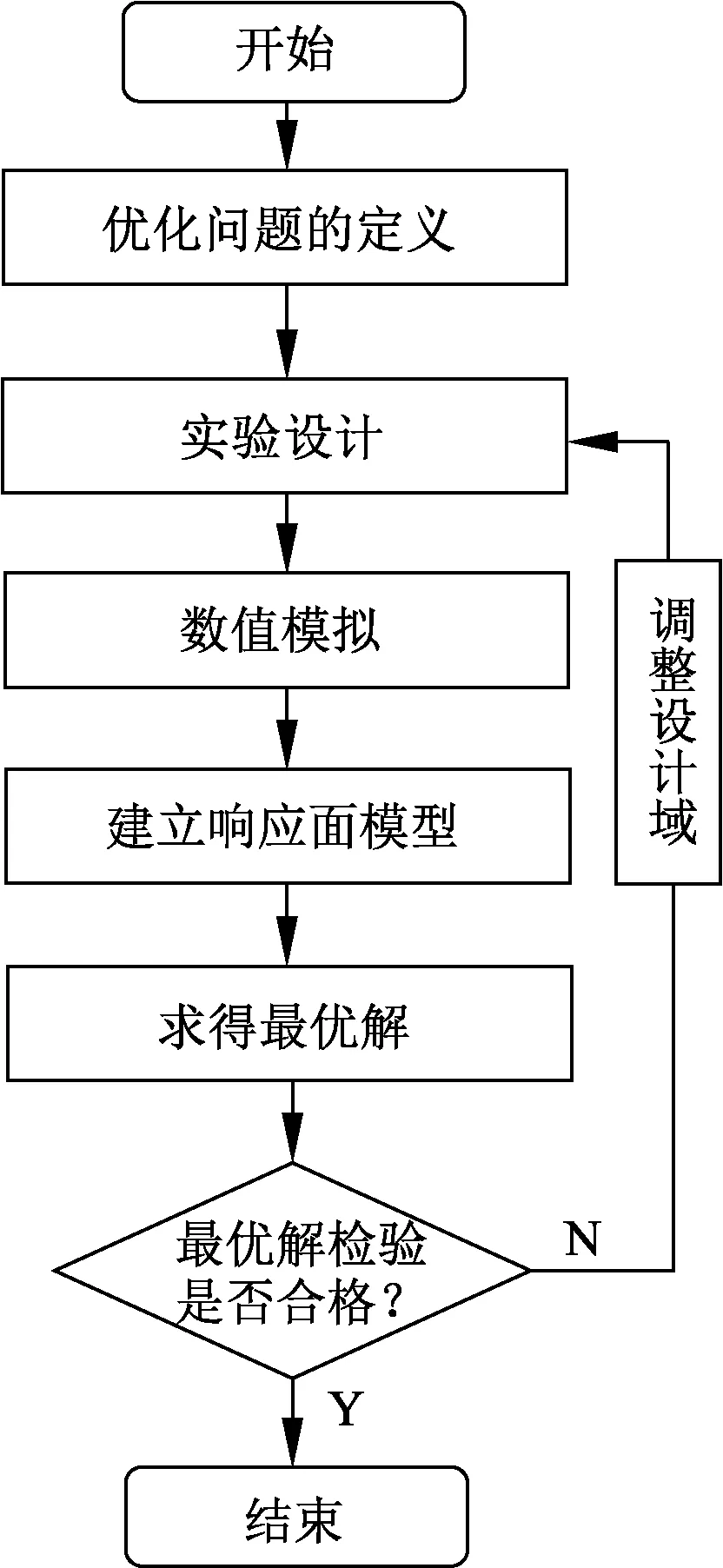
图15 响应面法的优化流程

SEA和CLE是评价耐撞性能的两个重要指标，SEA越大，结构的吸能效率越大.因此，将SEA作为优化设计的目标函数，CLE≤15 kN为优化设计的约束条件，BTS截面变厚度优化问题的表达为：

(5)

实验设计采用拉丁超立方随机抽样法，表3是选取的样本点以及仿真得到的响应值.

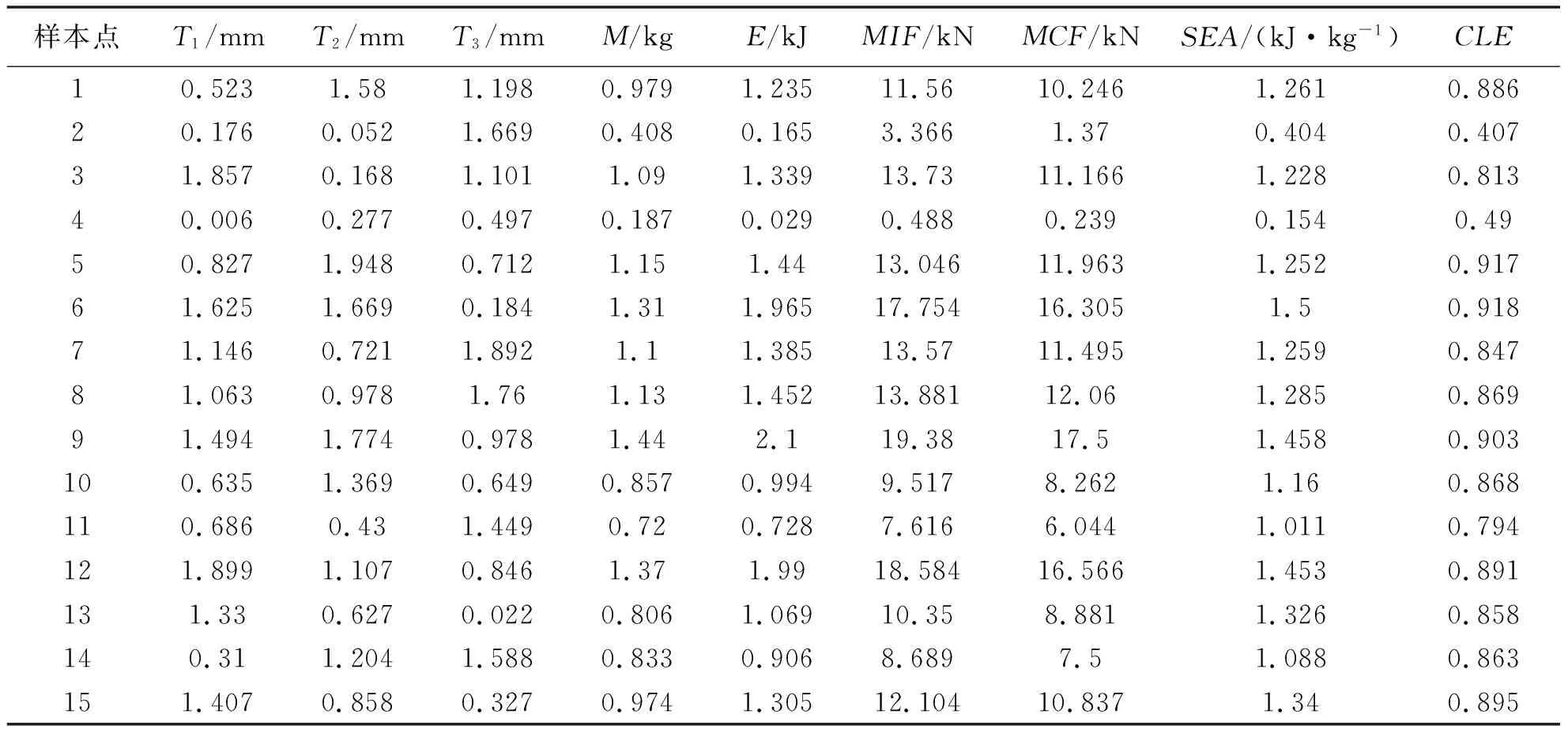
表3 样本点及其响应值

由于多项式回归分析经常用来处理非线性力学的设计优化问题，因此采用二次多项式函数.通过最小二乘法，对SEA和MIF进行拟合，SEA和MIF的响应面模型如下：

(6)

(7)

求得响应面模型最优解为SEA=1.45 kJ·kg-1，MIF=15 kN与其相应的壁厚为：T1=1.82 mm，T2=0.82 mm，T3=0.1 mm.由于要检验最优解的可信度，因而要对相同结构参数的BTS进行仿真模拟.模拟得到的SEA为1.45 kJ·kg-1，响应面模型预测的结果与仿真结果相差3.97%，误差在可接受的范围内.因此，响应面模型求得的最优解可信度高.为了体现BTS截面变厚度优化的优越性，将均匀厚度的BTS与最优厚度的BTS进行比较分析.图16为均匀厚度与最优厚度BTS的比较，均匀厚度和最优厚度BTS的力与位移曲线呈现相同的趋势，接触力随着位移先增大后趋于平稳.并且，最优厚度BTS的接触力在平稳期一直大于均匀厚度BTS的接触力，如图16(a).由图16(b)可知，最优厚度BTS的SEA值比均匀厚度BTS的SEA值高9%，优化后的BTS的能量吸收效率较传统的圆管提升了49.5%.

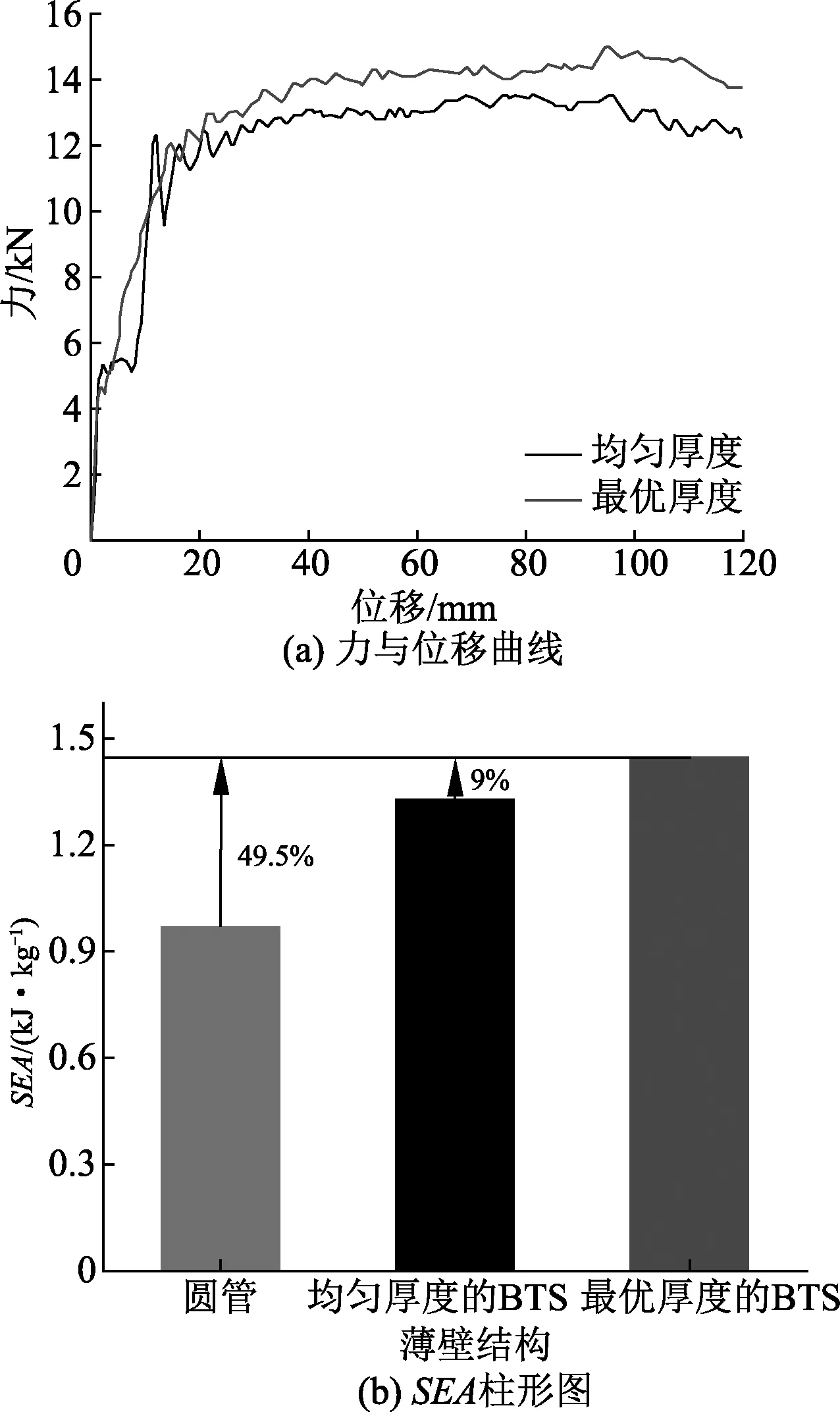
图16 均匀厚度与最优厚度BTS的对比

为了进一步了解最优厚度BTS与均匀厚度BTS能量吸收效率的差异，将最优厚度与均匀厚度的BTS的变形模式进行了比较，如图17.

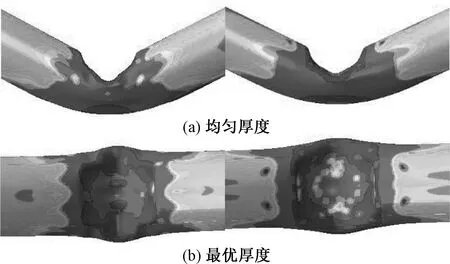
图17 BTS的变形模式

从图17可以看到，虽然最优厚度与均匀厚度的BTS的外凸和内凹皱褶数目一样，但其内凹皱褶有效接触面积却存在较大的差异.最优厚度BTS的有效接触面积大于均匀厚度BTS的接触面积，这也就是为什么最优厚度BTS的能量吸收效率要大于均匀厚度BTS能量吸收效率的原因.因此，可以说明BTS的截面变厚度优化可以提高能量吸收效率，并改善其耐撞性能.

6 结论

文中选择荷叶脉络为生物原型，设计出一种具有叶脉分支特征的薄壁结构，仿生薄壁结构(BTS).基于非线性动力学软件ABAQUS，研究了BTS的耐撞性能,并对BTS进行了截面变厚度优化设计，得到如下结论：

(1)冲击速度对BTS的耐撞性有一定的影响，碰撞峰值力随冲击速度的增加而增加.同时，冲击速度的增大对BTS的变形模式没有明显的影响.

(2)比值γ、主干数目N和壁厚T对BTS的耐撞性有着重要影响，适当增加γ值可以有效提高BTS的吸能特性;通过增加主干数目，可以有效提高BTS的吸能特性, 当N>6时，增大N值对提高BTS的耐撞性有着更好的增益效果;壁厚T≤2mm时，增大壁厚对于提高BTS的耐撞性有着更好的增益效果.

(3)采用响应面法，以壁厚T和MIF为约束条件，SEA为优化目标对BTS进行截面变厚度优化设计，获得了BTS的最优截面厚度.BTS的截面变厚度优化可以提高能量吸收效率，并改善其耐撞性能.