基于自发漏磁效应的钢绞线应力检测试验研究
2022-04-21刘尚凯周建庭张向和赵瑞强张潇汀
刘尚凯,周建庭,张向和,赵瑞强,张潇汀
(1. 重庆交通大学 土木工程学院,重庆 400074; 2. 重庆市市政设施管理局,重庆 400015;3. 重庆交通大学 材料科学与工程学院,重庆 400074)
0 引 言
拱桥以其独特的优势,成为现今大跨度桥梁的最主要桥型之一[1],吊杆作为拱桥主要受力结构[2],准确检测其应力状态对桥梁科学管养和维修决策具有至关重要的作用[3]。钢绞线由于具有强度高、在结构中排列安置方便且易于锚固等优点被广泛的运用于吊杆中[4],研究钢绞线的应力状态有助于更好的了解实际吊杆的受力状态[5]。
索力值是衡量钢绞线结构是否处于正常工作状态的重要标志[6]。常见的索力测量方法如千斤顶张拉法[7],频率法[8],压力传感器法[9],磁通量法[10]等存在测量精度低、仪器使用不便、数据处理繁琐等问题。钢绞线是一种典型的铁磁性材料[11],该类材料在外部工作载荷和地磁场的共同作用下,其应力集中位置将发生磁畴组织的定向和不可逆的重新取向,在构件表面形成微弱的漏磁场,这种现象被称为自发漏磁效应[12-13]。
基于自发漏磁效应的无损检测技术拥有着测量精度高、仪器轻便且抗干扰性好等特点,被广泛的应用于管道、液压容器、储存罐等铁磁性构件的质量检测中[14]。董丽虹等[15]研究了磁记忆信号对不同应力集中程度,疲劳裂纹及残余应力的反映;X. FANG等[16]建立了可以利用等效磁场来表示应力作用效应的数学理论模型,其研究表明金属材料在受拉或受压时,其材料内部的磁化强度将会出现负增长;杜磊等[17]利用开发出的金属磁记忆检测仪对拉伸钢棒进行测量,对所得数据采用一维小波降噪处理,以确定其应力集中区;PANG Caoyuan等[18]研究了加载过程中裸筋与外包混凝土所受拉力与漏磁信号的特征关系,提出了通过漏磁信号推导钢筋受力状态的方法。
综上所述,基于自发漏磁效应的无损检测技术在检测铁磁材料的微观损伤与应力集中上应用较多,基于此技术的钢筋应力测量也有不少的研究,但在漏磁信号与钢绞线所受拉力相关性问题方面鲜有报道。笔者以钢绞线为对象进行了系列试验研究,进一步探究了自发漏磁与钢绞线所受拉力之间的相关性,为吊杆钢索应力状态的测量打下基础。
笔者研究了钢绞线所受拉力F与其漏磁场B的对应关系,并探索了此关系受试件长度L与提离高度Z影响的情况,具体的研究流程如图1。

图1 研究流程Fig. 1 Research process
1 试验过程
1.1 试件制备
本试验以1 860级低松弛预应力钢绞线为试验对象,该类钢绞线直径15.24 mm、抗拉强度标准值1 860 MPa,采用水冷切割以减少加工过程对于钢绞线漏磁场的影响。试验中钢绞线的截面积取140 mm2进行计算,则其理论破断值对应的拉力为140×1 860=260.4 kN,作为预应力构件的钢绞线极限承载力取破断值的60%~65%,本试验中取62.5%,即260.4×62.5%=162.75 kN。
为减少加工过程对漏磁场的影响,采用水切割法对同一批次的钢绞线进行加工,制成不同长度的钢绞线试件,编号为C1~ C5,各编号试件分别设置3组重复性试验。为探究不同试件长度L、不同提离高度Z(磁探头中心与钢绞线的距离)对漏磁信号的影响,本试验设置2个对照组。以C1为标准试件,对照组1包括C2、C3,对照组2包括C4、C5,试件的具体参数与分组情况如表1。

表1 试件参数Table 1 Specimen parameters
1.2 试验设备
加工后的试件采用WAW-1000微机控制电液伺服万能试验机,以N级在上、S级在下的方向进行固定,两端采用18 cm的铝制夹片进行夹持,夹持长度为15 cm。钢绞线表面漏磁信号选用HMR2300三轴微磁传感器进行采集,并通过NetPort串口传入信号接收器,以进行数据存储与处理。相关设备如图2。
传感器中心位置水平对齐钢绞线试件轴向L/2处,仪器的连接方式与摆放位置如图3。

图2 试验设备Fig. 2 Test equipment

图3 试验设备布置示意Fig. 3 Schematic diagram of test equipment layout
1.3 试验方案
张静等研究了构件在单向拉伸应力状态下的磁记忆检测信号特征,发现当铁磁材料在进行匀速拉伸时,其表面漏磁场呈规律性变化,且漏磁信号曲线在特定应力值下存在明显的转折点,可以用以判断试件所处的应力阶段[19]。因此,本试验进行钢绞线试件匀速拉伸,研究试件表面漏磁信号与所受拉力间的关系。
在液压万能试验机上对标准钢绞线试件进行加载,采用5 mm/min的速度进行匀速拉伸,从0 kN加载到200 kN。钢绞线试件加载过程中磁传感器测得随时间变化的漏磁场强度B,万能试验机测得钢绞线所受拉力大小F随时间的变化情况。分析力学信号与磁信号的变化趋势、对应关系,并绘制力-磁曲线。
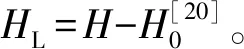
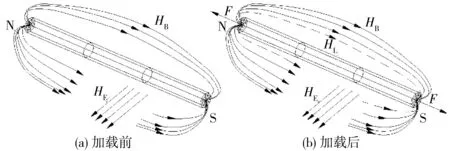
图4 钢绞线加载前后磁场分布示意Fig. 4 Schematic diagram of magnetic field distribution before andafter steel strand loading
2 试验结果及分析
2.1 漏磁场变化情况与影响因素
图5给出了加载过程中,试件C1表面漏磁场各方向分量随所受拉力的变化曲线,其中Bx、By与Bz皆为磁传感器测量值减去试件自身磁场与地磁场的结果,表示由加载引起的钢绞线表面漏磁场在测点处的变化情况。
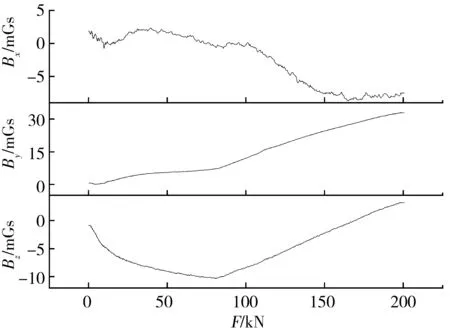
图5 试件C1漏磁场强度随所受拉力变化关系Fig. 5 The relationship between the strength of the leakage magneticfield of specimen C1 and the tensile force
由图5可知,在加载过程中,随着所受荷载F的增加,钢绞线表面漏磁场呈规律性变化:漏磁场的切向分量Bx波动较大,整体呈下降趋势;漏磁场的法向分量By较为稳定,整体呈上升趋势;漏磁场的分量Bz先减小再增大,存在明显的转折。由于漏磁场法向分量By与荷载F的有着较好的单映射关系,且By-F曲线较为光滑,故选择漏磁场法向分量进一步研究,并以相同方法处理其余4组试件,绘制By-F曲线,以进一步研究其对应关系,结果如图6。

图6 漏磁场法向分量By随所受拉力F变化关系Fig. 6 The relationship between the normal component of leakagemagnetic field By and the tensile force F
由图6可知,在相同的加载工况下,5组试件的漏磁曲线形状具有一致性,但数值上有明显的差值。即加载过程中,试件的漏磁场呈规律性变化,By与F正相关,其梯度随加载过程而变化。这表明钢绞线所受的拉力F、钢绞线试件长度L与提离高度Z都会影响钢绞线表面漏磁场。为探究自发漏磁与钢绞线受力的关系,需要采用控制变量的方法,分别研究以上三因素对自发漏磁的影响。
2.2 加载过程自发漏磁信号的变化
图7给出了试件C1的By-F曲线、参照线以及Ky-F曲线。其中By与F非线性相关,但通过与参照线的对比,能够更好的研究By-F曲线的分布情况。为进行定量分析,对By-F曲线进行求导,得到漏磁场法向强度对于所受拉力的一阶偏导数Ky=dBy/dF,Ky表示的By梯度,并进行曲线拟合,得漏磁场法向分量梯度曲线Ky-F。

图7 By-F关系图与Ky-F关系Fig. 7 By-F diagram and Ky-F diagram
由图7可知,漏磁场的法向分量By变化与钢绞线受拉力F正相关,但线性较差。对比参照线,在F=18.56~112.87 kN内,By-F曲线产生了明显的“凹陷”,即其梯度在该区间内发生了明显的变化,通过Ky-F曲线对By-F曲线的变化情况进一步分析。Ky-F曲线在F=6.25 kN时过0点,即By-F曲线在F=0~6.25 kN间呈下降趋势,在F=6.25~200 kN间呈上升趋势。这是由于拉伸初期,钢绞线内部存在大量无序排列磁畴,受拉使得磁畴组织重新取向排列以抵消增加的机械能,期间漏磁场强度减小。随着荷载逐渐增大,受拉钢绞线会发生磁致伸缩效应和磁畴组织定向运动,磁导率增大进而形成磁极[21],此时By随着F的增大而单调递增。Ky-F曲线在F=0~18.06 kN与57.48~112.87 kN内分别递增,在F=18.06~57.48 kN与112.87~200.00 kN内分别递减,即Ky-F曲线在加载过程中存在3个转折点,分别是18.06、57.48、122.87 kN。
本试验采用φs15.24(1×7)1 860级镀锌钢绞线,作为预应力构件的钢绞线极限承载力取破断值的60%~65%,本试验中取62.5%,即162.75 kN。则以上转折点分别对应11.08%、35.32%与75.50%极限承载力,现将这3点定义为特征点A、特征点B与特征点C。这是由于拉伸过程中钢绞线内部磁导率非线性增大,致使漏磁强度产生畸变所导致的[21]。
2.3 提离高度与试件长度对漏磁场的影响
上述结果显示,加载过程中By-F曲线呈规律性变化,且Ky-F曲线存在特征点。如图8,将2对照组的漏磁场法向分量绘出,以探究By-F曲线的一般性规律,以及试件长度L与提离高度Z对自发漏磁的影响。
如图8(a),当试件长度一定时,漏磁场切向分量By随着所受荷载F的逐渐增加呈规律性变化:当提离高度为1 cm和2 cm时,By与F呈正相关,且曲线存在“两端陡、中间平缓”的现象;当提离高度为4 cm时,By随着F的增加先减小后增大,整体上接近一根水平直线,这是由于该提离高度下,外界磁场对漏磁场的影响较大造成的。这表明随着提离高度的增大,测得的By-F曲线逐渐平缓,漏磁场强度变化范围逐渐减小。
如图8(b),当提离高度一定时,漏磁场切向分量By随着所受荷载F的逐渐增加呈规律性变化,By与F呈正相关,且曲线存在“两端陡、中间平缓”的现象。当L=50 cm时对应的By-F曲线变化值与变化率都明显大于其他试件,这可能是由于当钢绞线试件较短时,测点离两端较近,端头效应较为明显所导致的。这表明随着试件长度的增大,测得的By-F曲线变化率趋于定值,By与F接近线性相关。

图8 不同影响因素下By-F关系Fig. 8 By-F relationship diagram under different influencing factors
2.4 基于漏磁场的钢绞线应力分级测量
仿照试件C1的处理方式,求出各组数据所对应的法向分量梯度曲线Ky-F,如图9,求出特征点位置、各试件参数与分析结果汇总于表2中。
由图9与表2可知,试件1与试件2的Ky-F曲线存在3个明显的转折点,试件3、试件4以及试件5,则存在2个明显的转折点。当提离高度为1 cm时,其Ky-F曲线的转折点对应的F值明显偏离其他试件,根据磁偶极子理论,这可能是由于当提离高度较小时,试件靠近传感器部分的磁致伸缩对于测点处影响较大,而提离高度较大时,试件各部分磁致伸缩相互耦合共同影响测点处磁场的变化所造成的。由于实际中各种测量环境都要求较大的提离高度,同时特征点A对应的F值较小,且后3组Ky-F曲线呈“S”型分布不存在特征点A,这可能是加载初期,磁畴由不均匀分布转为均匀排列,力-磁关系更为复杂所导致的。故对除试件C2外的4组数据的特征点B、特征点C取均值,结果为50.84 kN与116.84 kN,对应的方差为5.45与3.03,离散性较弱。本试验采用作为预应力构件的钢绞线极限承载力为162.75 kN,即以上两个特征点分别对应极限承载力的31.24%与71.79%。以这两点为分界点,可将钢绞线从开始加载(0 kN)到极限承载力(162.75 kN)的过程分为3个加载阶段。各试件加载过程分级结果如图10,不同色块表示每组试件对应的3个加载阶段分别占极限承载力的百分比,“综合”栏表示依据5组数据最终得到的分级标准。

图9 各组试件的Ky-F关系Fig. 9 Ky-F relationship diagram of each group of specimens
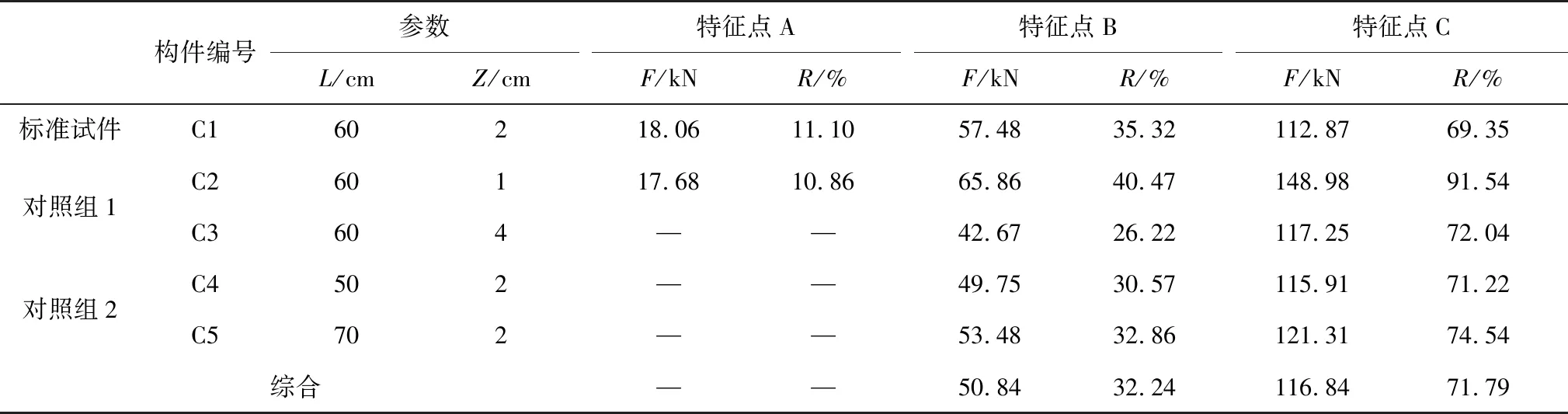
表2 曲线特征汇总Table 2 Summary of curve features
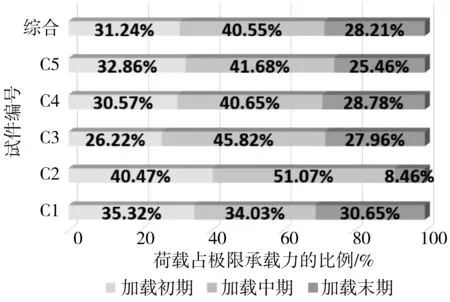
图10 加载阶段分级Fig. 10 Loading stage classification
由图10可知,加载过程可按漏磁强度法向分量的变化率拟合曲线的单调性分为3个阶段,以31.24%与71.79%的极限承载力为分界点,分为加载的前期、中期与后期:
1)在加载初期,0~31.24%极限承载力阶段,Ky-F曲线先递增再递减或单调递减;
2)在加载中期,31.24%~71.79%极限承载力阶段,Ky-F曲线单调递增;
3)在加载后期,71.79%~100%极限承载力阶段,Ky-F曲线单调递减。
3 结 论
对1 860级镀锌钢绞线进行张拉,并分析了钢绞线表面漏磁信号与所受拉力的变化规律,主要研究结论如下:
1)随着所受拉力的增加,钢绞线表面漏磁场法向分量By-F曲线存在“两侧陡,中间平缓”的现象,其梯度在加载过程中发生明显变化。
2)漏磁法向分量梯度曲线Ky-F存在两个转折点,可将加载过程分为3个阶段。各阶段具有不同的单调性,通过计算单调性可判定钢绞线受拉所处的加载阶段。
3)随着提离高度的增大,加载过程中漏磁场强度的变化范围减小;随着试件长度增大,By-F曲线的变化率趋于稳定。
4)基于自发漏磁效应对钢绞线应力值进行了分级评估,在实现更精确的应力值测量上还需要更深入的研究。若要应用于吊杆应力测量,则还需解决多根钢绞线漏磁场相互耦合以及PE护套对漏磁场的影响等问题。
