滑坡推力与安全系数计算方法适用性研究

李焕焕，倪万魁，陈树峰，李 刚

(1. 西京学院 陕西省混凝土结构安全与耐久性重点实验室，陕西 西安 710123；2. 长安大学 地质工程与测绘学院，陕西 西安 710054)

0 引 言

滑坡推力是影响抗滑桩设计可靠性的一个重要参数。我国现行规范推荐采用传递系数法来计算滑坡推力，包括传递系数显式解法与传递系数隐式解法。不同行业规范推荐的解法不同，比如TB 10025—2006《铁路路基支挡结构设计规范》、JTG/T 3334—2018《公路滑坡防治设计规范》、GB 50021—2001《岩土工程勘察规范》等建议采用传递系数显式解法来计算稳定系数与滑坡推力，而GB 50330—2013《建筑边坡工程技术规范》、SL 386—2007《水利水电工程边坡设计规范》、GB 51016—2014《非煤露天矿边坡工程技术规范》等建议采用传递系数隐式解法计算稳定系数与滑坡推力。

我国研究人员[1-5]通过考虑不同的影响因素，对传递系数法进行了改进；林峰等[6]通过对条块间作用力的方向假定进行修正，改进了传递系数法；陈栋等[7]提出了考虑滑坡主滑方向的矢量和稳定性分析方法；陶志平等[8]指出显式解法计算滑坡推力的力学意义不明确，而隐式解法计算滑坡推力偏小，提出了考虑滑体重力增大与滑面强度降低的改进传递系数隐式解法；苏爱军[9]认为在给定安全系数情况下，隐式解法计算得到的安全系数偏小；杨涛等[10]指出传递系数法不能正确计算滑面强度相同而滑体强度不同的滑坡推力，提出了采用拉格朗日差分法来计算滑坡推力的方法；WANG Yang等[11]研究得出水位变化产生动水压力影响边坡稳定性的结论，并提出了基于极限平衡分析的稳定性计算修正模型；ZHANG Zhenhua等[12]针对水库水位波动这一影响因素，提出了考虑动水压力的传递系数改进方法，并通过与监测结果的对比验证了方法的合理性；XIAO Shiguo[13]指出相邻条块之间可能存在剪切失效的状态，提出了考虑条块界面安全系数的传递系数改进方法，该方法比传统传递系数法更保守，适用于实际工程；黄成等[14]考虑坡体的破碎程度，提出了传递系数改进算法；赵尚毅等[15]指出无论是显式解法还是隐式解法计算得到的滑坡推力作为支护力施加到滑坡模型上所达到的安全系数不等于设计安全系数，提出了考虑桩反作用力和设计安全系数的传递系数隐式解法改进公式。

传递系数显式解法是工程中常用的一种滑坡推力计算方法。因此，笔者在文献[15]基础上考虑桩反作用力改进传递系数显式解法，并依托FLAC 3D软件平台，应用强度折减法论证改进方法的有效性。另外，笔者进一步探讨了传递系数显式解法、隐式解法，改进的传递系数显式解法、隐式解法等4种方法计算滑坡推力的适用性，分析了强度折减法及传统极限平衡法计算滑坡安全系数的区别，并提出了推荐的滑坡推力和安全系数计算方法。

1 传递系数显式解法

1.1 传统显式解法

传递系数法显式解法(为了与笔者在文中提出的“改进显式解法”进行区别，简称“传统显式解法”)属于传递系数法的一种解法，其基本假定主要包括：条块间传递压力不传递拉力；条块间的作用力以集中力的形式作用在条块分界面的中点，方向与上一条块的滑动方向平行。取滑坡主滑方向单宽土带作为分析对象，不考虑土条侧面摩擦力的影响，其计算简图如图1。

图1 传统显式解法计算简图Fig. 1 Calculation diagram of conventional explicit solution method

对于第i条块，切向力Ti、法向力Ni分别按式(1)、式(2)计算：

Ti=Fi-Fi-1cos(θi-1-θi)-Wisinθi

(1)

Ni=Fi-1sin(θi-1-θi)+Wicosθi

(2)

式中：Fi为i条块的支撑力，kN；Fi-1为i-1条块的向下传递的推力，kN；θi、θi-1分别为i、i-1条块滑动方向与水平方向的夹角，(°)；Wi为i条块自身的重力，kN。

由极限平衡条件，得

Fi-Fi-1cos(θi-1-θi)-Wisinθi+[Fi-1sin(θi-1-θi)+Wicosθi]tanφi+cili=0

(3)

式中：φi为i条块滑面处内摩擦角，(°)；ci为i条块滑面处黏聚力，kPa；li为i条块滑面长度(弧度)，m。

传统显式解法是通过增加下滑力来计算滑坡推力，考虑设计安全系数Ks，变换式(3)得到沿滑面方向推力P′(单位：kN)：

P′=ψi-1Fi-1+KsWisinθi-Wicosθitanφi-cili

(4)

式中：ψi-1为i-1条块的传递系数，ψi-1=cos(θi-1-θi)-sin(θi-1-θi)tanφi。

工程中，按式(5)计算作用在抗滑桩上的水平滑坡推力P：

P=P′cosθi

(5)

1.2 改进显式解法

考虑桩的反作用力P(即抗滑桩承担的水平滑坡推力)作用在设桩处条块(假设设置抗滑桩处的土体条块为n)，建立极限平衡条件。计算简图如图2。

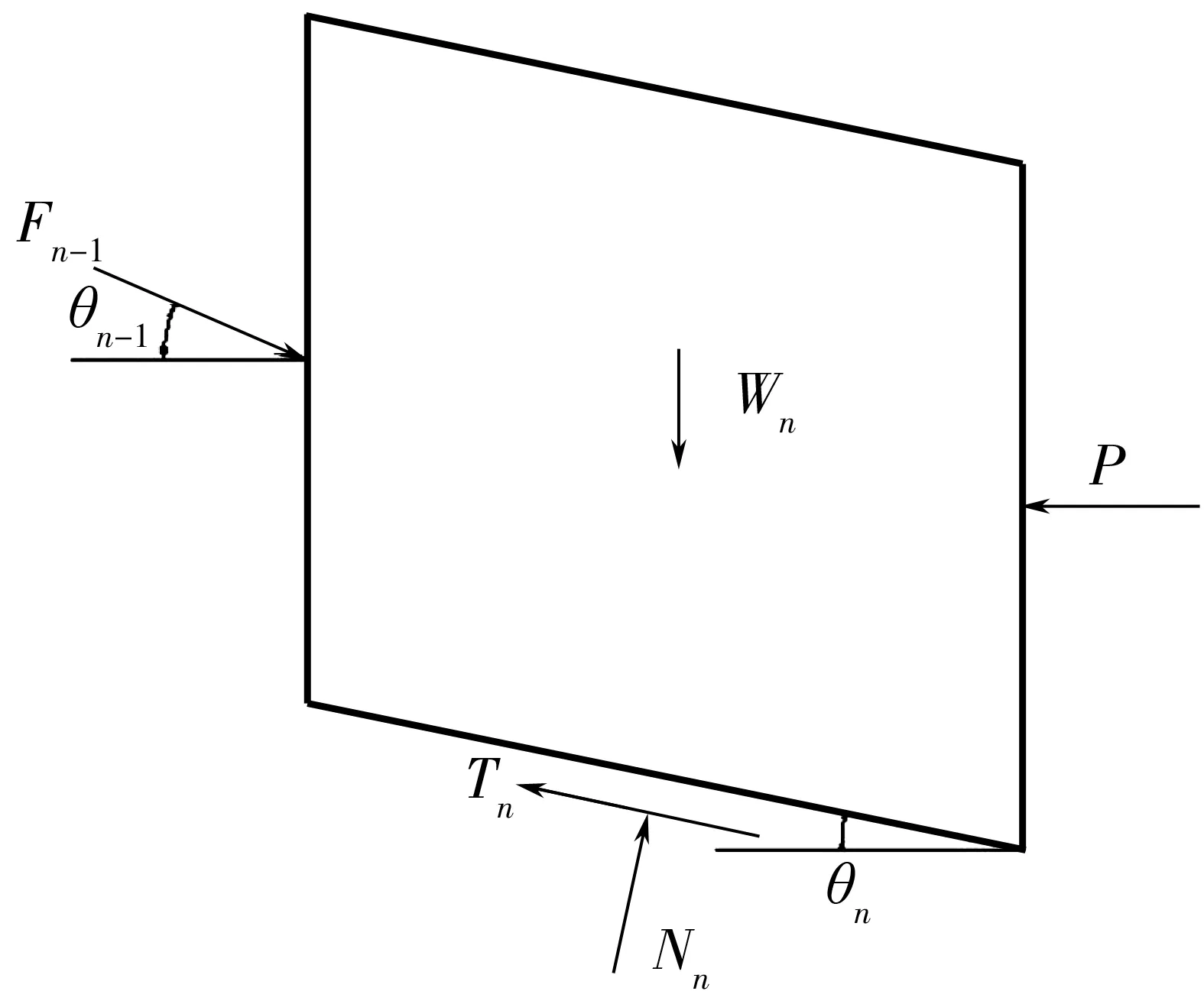
图2 改进显式解法计算简图Fig. 2 Calculation diagram of improved explicit solution method

考虑设计安全系数Ks，由极限平衡条件可得

Pcosθn-Fn-1cos(θn-1-θn)-KsWnsinθn+

[Fn-1sin(θn-1-θn)+Wncosθn+Psinθn]tanφn+

cnln=0

(6)

整理得

(7)

1.3 算例分析

选取如图3的计算模型来验证改进显式解法〔式(7)〕计算结果的可靠性。滑体垂直高度h=20 m；滑面为直线型，倾角θ=30°，滑面长度l=40 m；滑体材料重度r、弹性模量E、泊松比μ、黏聚力c、内摩擦角φ见表1，可计算出滑体重力W=8 660.25 kN。取滑坡设计安全系数Ks=1.35。

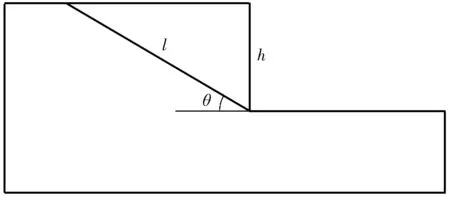
图3 算例模型Fig. 3 Example model

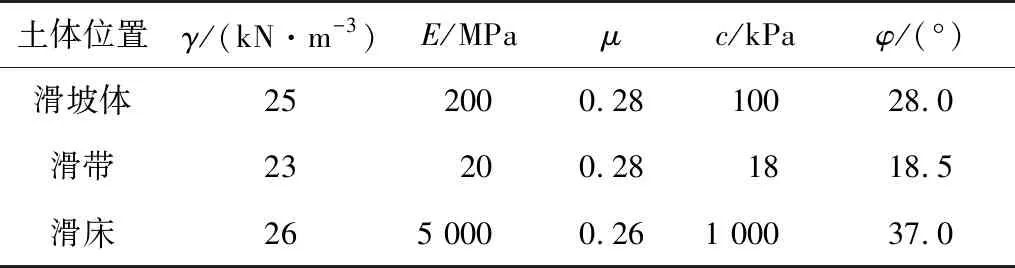
表1 滑坡体材料的物理力学参数Table 1 Physical and mechanical parameters of landslide materials

将滑坡体相关参数分别代入式(4)、式(5)及式(7)，可计算得到采用传统显式解法、改进显式解法的水平滑坡推力P。

1)传统显式解法

P=P′cosθ=(KsWsinθ-Wcosθtanφ-cl)cosθ=

(1.35 × 8 660.25 × sin30° - 8 660.25 × cos30° ×

tan18.5° - 18 × 40)cos30°=2 265.70(kN)

2)改进显式解法

2 531.81(kN)

可见，用改进显式解法计算得到的滑坡推力值大于用传统显式解法计算的。

2 数值验证

为了验证传统显式解法和改进显式解法计算结果的可靠性，将计算得到的滑坡推力P作为外力施加在坡体右侧临空面上，建立FLAC 3D数值模型，采用强度折减法计算2种情况下的滑坡安全系数。

2.1 FLAC 3D数值模型建立

为了提高计算效率，仅在y方向取10 m进行计算，最终模型尺寸为100 m × 10 m × 40 m，滑带厚0.5 m。设桩位置位于x=70 m处。分组模型如图4。

图4 分组模型Fig. 4 Grouping model

选取Mohr-Coulomb模型为土体本构模型，土体重度γ、弹性模量E、泊松比μ、黏聚力c、内摩擦角φ等参数见表1。模型边界约束条件为：

1)x=0与x=100 m为x向约束；

2)y=0与y=10 m为y方向约束；

3)z=0 m为三向固定约束，z=40 m为自由边界。

2.2 计算步骤

1)计算初始地应力，平衡后将速度位移清零。

2)将设桩处前缘土体挖除，即分组为“wa”(图4)的部分定义为空模型。

3)依据土层条件，假设滑坡推力P呈矩形分布，则由传统显式解法、改进显式解法计算的滑坡推力分布荷载q分别为113.285、126.590 kPa。

4)在设桩位置施加计算得到的滑坡推力分布荷载q，设置模型土体参数，并采用强度折减法计算安全系数Ks，当坡体处于极限平衡状态时，折减系数fs即为安全系数Ks。

2.3 计算结果分析

图5为极限平衡状态时(fs=1.26、1.36)坡体的最大剪应变增量云图与塑性区分布云图；图6为破坏状态时(fs=1.27、1.37)坡体的最大剪应变增量云图与塑性区分布云图。从云图可以判定坡体是否处于极限平衡状态。

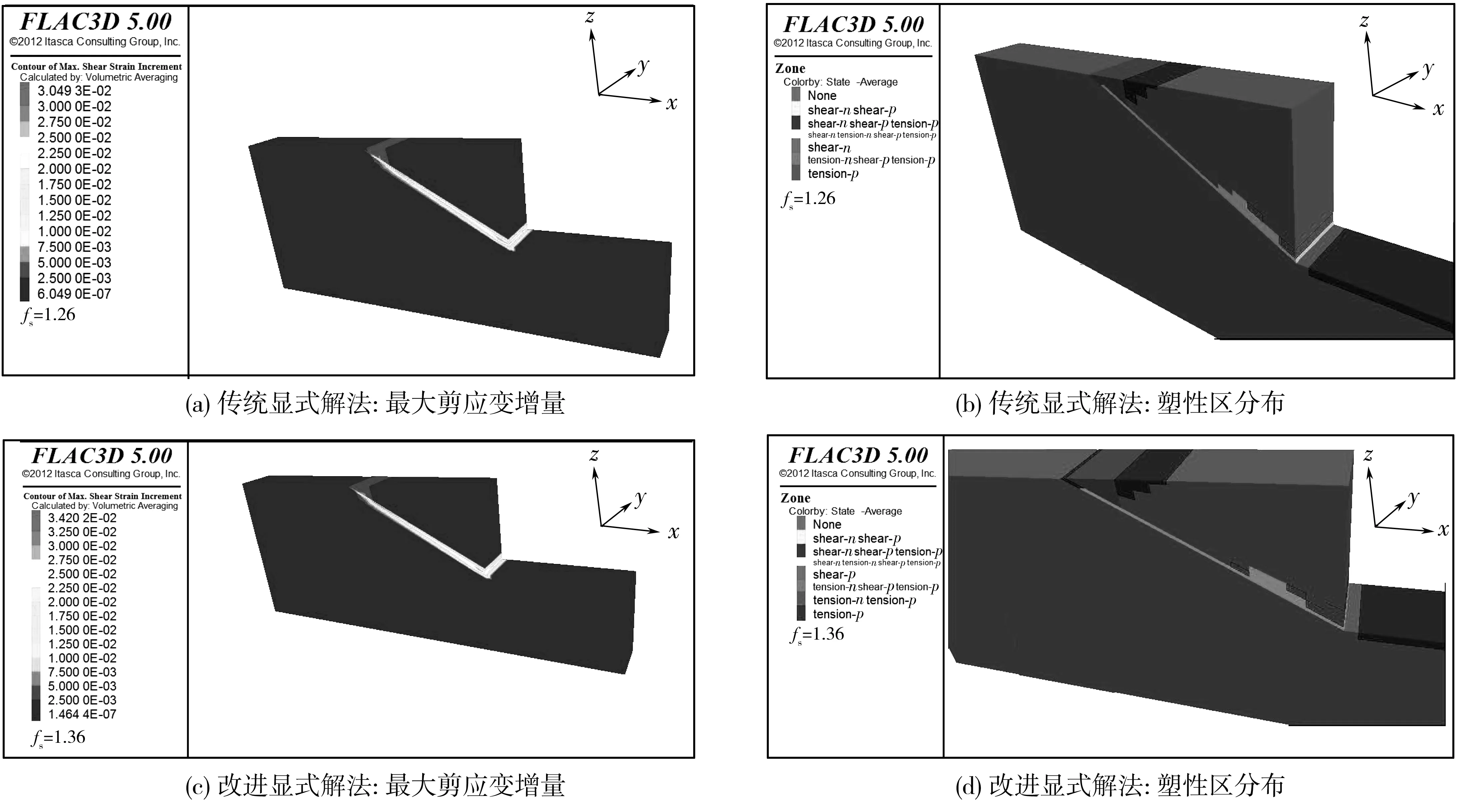
图5 极限平衡状态时最大剪应变增量、塑性区分布云图Fig. 5 Nephogram of maximum shear strain increment and plasticity distribution in limit equilibrium state

图6 塑性破坏状态时最大剪应变增量、塑性区分布云图Fig. 6 Nephogram of maximum shear strain increment and plasticity distribution in plastic failure state

1)图5(a)坡脚附近滑带的最大剪应变增量最大，后缘处最大剪应变增量非常小，为10-3量级；图6(a)滑带整体最大剪应变增量值均较大。对比可知，图5(a)滑面没有完全贯通，滑坡处于极限平衡状态；图6(a)滑面已经贯通，处于塑性破坏状态。

2)图5(b)滑带中前部均处于塑性状态，呈现剪切破坏；图6(b)滑带整体处于塑性变形阶段，中前部呈现剪切破坏，后部为拉破坏。对比可知，图5(b)处于极限平衡状态，滑带没有完全处于塑性状态；图6(b)滑坡体已经发生了滑动，滑坡处于不稳定状态。

3)图5(c)滑面中前部最大剪应变增量值较大，后缘增量很小；图6(c)滑带处剪应变增量值远远大于图5(c)最大剪应变增量值。对比可知，折减系数fs=1.36时，滑面整体最大剪应变增量均很小，滑坡处于极限平衡状态；fs=1.37时，滑带已经贯通，处于不稳定状态。

4)图5(d)滑带中前部处于塑性阶段，为剪切破坏，滑体后缘没有达到塑性状态；图6(d)整个滑带均处于塑性变形状态，滑带中前部为剪切破坏，后部为张拉破坏。对比可知，fs=1.36时，滑面没有完全贯通，处于极限平衡状态；fs=1.37时，滑面贯通，滑坡处于不稳定状态。

综上所述，将传统显式解法计算得到的滑坡推力均布施加在设桩处条块，计算得到的安全系数为1.26，不能达到设计安全系数1.35的要求；将改进显式解法计算得到的滑坡推力施加在设桩处条块，计算得到的安全系数为1.36，达到设计安全系数1.35，满足设计要求。结果验证了改进显式解法的可行性与可靠性。

3 显式解法与隐式解法对比分析

表2为采用传统显式解法、改进显式解法，与传统隐式解法及改进隐式解法[15]计算得到的滑坡推力值。

表2 滑坡推力计算结果Table 2 Calculation results of landslide thrust kN

由表2可知：无论是传统方法还是改进方法，显式解法的计算结果均大于隐式解法的计算结果；无论是显式解法还是隐式解法，改进方法计算结果均大于传统方法计算结果。分析原因，显式解法是基于极限平衡法来计算安全系数的，而隐式解法是通过强度折减进行迭代来计算安全系数的，2种方法的计算原理不同，最终计算结果也不尽相同。极限平衡法计算得到的滑坡推力相对强度折减法的计算结果是偏大的。

笔者是将基于极限平衡法计算得到的滑坡推力值反作用于滑坡体上，再采用强度折减法计算安全系数的，安全系数计算值达到了设计安全系数；而赵尚毅等[15]是将基于强度折减法计算得到的滑坡推力值反作用于滑坡体上，再采用极限平衡法计算安全系数的，最终安全系数计算值也达到了设计安全系数。经分析可知，采用强度折减法计算得到的安全系数值比采用极限平衡法计算得到的安全系数值小。因此，为了确保安全，建议采用改进的传递系数显式解法来计算滑坡推力，而采用传统的传递系数隐式解法来计算滑坡安全系数。

4 结 论

考虑桩反作用力，推导了传递系数显式解法改进公式，通过FLAC 3D软件建立模型，采用强度折减法验证了改进方法的合理性；探讨了显式解法、隐式解法计算滑坡推力与安全系数的适用性。主要研究结论如下：

1)由改进显式解法计算得到的滑坡推力值大于由传统显式解法计算的；按照改进显式解法计算得到的滑坡推力进行滑坡治理设计可以达到设计安全系数。

2)采用强度折减法计算得到的滑坡推力值相对于采用极限平衡法计算的偏小，安全系数也偏小；相反，采用极限平衡法计算得到的滑坡推力值相对于采用强度折减法计算的偏大，安全系数也偏大。因此，建议采用改进的传递系数显式解法来计算滑坡推力，采用传统的传递系数隐式解法来计算滑坡安全系数。