“双减”背景下数学作业设计探索

江苏省锡山高级中学实验学校第一小学 陈樱红

作业是课堂教学的必要延伸，发挥着诊断、指导、检验、评价的功能。在学习完新知之后，适当适量的作业能起到内化和建构课堂知识、反馈学习效果的重要作用，在学生学习数学的过程中不可或缺。学生通过作业巩固所学知识，在练习的过程中形成相应的技能和思维方法，感悟数学学科思想，培养实践能力和探索精神。

“双减”背景下，作业设计推到了教学研究的前沿。“双减”的任务之一就是要减轻学生的作业负担。作业“减什么”“怎么减”，是学校教学作业改革的关键所在。以往的数学作业多存在以书面作业为主，形式相对单一，作业内容千篇一律，缺乏层次性，作业效果侧重结果、不注重过程等问题。就小学数学学科而言，应该基于学生的年龄特点和学习规律，设计形式多样、内容有趣、过程丰满、富有思维、探究开放的作业，让学生既“作”有所获，又“作”有所乐。

一、丰富作业形式，丰实作业内涵

（一）巧妙关联，设计生活化作业

雷夫·艾斯奎斯在《第五十六号教室的奇迹》一书中，介绍了自己设计数学作业的方法。他千方百计让学生了解数字的威力，明白数学与生活息息相关。笔者从中得到启发，尝试把数学算式还原到生活场景中，赋予数学作业丰富的生活意义。

例如，教学三年级下册“含有小括号的混合运算”这节课时，教师可以设计如下练习题：

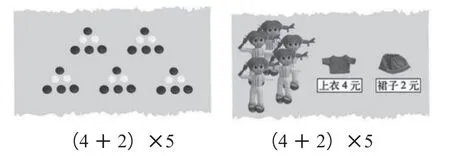
图1

（1）说一说：（4＋2）×5在上面两幅图中分别解决了什么问题？

（2）想一想：（4＋2）×5这个含有小括号的综合算式还能解决生活中的哪些问题？

解决实际问题的作业，传统教学是教师设计好习题，学生列式解答。在这里，教师让学生根据算式（4＋2）×5到生活中寻找与之匹配的实际问题原型。第一个问题“依据算式说图意”，引导学生初步感受算式在生活中的意义。算式（4＋2）×5在左边一幅图中表示有5堆棋子，每堆有4枚黑棋和2枚白棋，求一共有多少枚棋子；在右边一幅图中表示给5个布娃娃购买衣服，一件上衣4元，一条裙子2元，求一共需要多少钱。第二个问题“还能解决生活中的哪些问题”，学生需要把算式代入自己的生活，到生活中提取经验，深刻感受这个算式丰富的生活意义。这样的作业走进了每个学生的生活，在作业交流中可以使学生进一步感受到：虽然具体的问题情境不同，但都要先求出4与2的和，之后再乘5。

（二）凸显应用，设计实践型作业

美国教育家彼德·克莱恩说：“学习的三大要素是接触、综合分析、实际参与。”实践型作业正好符合以上三个要素，它的特点是突出数学活动的实践性， 使学生不仅会在纸上做数学，而且能在动手、动口、动脑中学数学，能运用所学知识开展调查 、收集、选择、分析、解释信息等活动。教师在设计数学作业时，要树立实践观念，敢于放手，让学生经历从实际问题抽象出数学问题的过程，并且能够主动分析问题，寻求解决问题的方法。

比如一年级学习完“认识人民币”这一单元后，正好赶上学校组织学生参加春季综合实践活动。有的教师敏锐地意识到这一契机，设了如下的数学实践作业：

同学们，明天到动物园参观，每人限带10元现金。在参观过程中，同学们可以单独购买商品，也可以两个人合起来购买商品。购买之前，先要看清商品的价格，再根据付出的钱算好找回多少钱。如果遇到困难，可以找小伙伴商量，也可以寻求老师的帮助。

这类实践作业，学生在真实的情境中使用人民币，不但再次巩固了对不同面值人民币的认知，而且对付出的钱、商品的价钱、找回的钱这三个数量之间的关系理解得更加深刻了。有的学生要买一袋15元的爆米花，钱不够，怎么办？遇到这样的情况，学生自己想出了不同的办法：有的“借钱买”，向同学借5元，自己一个人吃，下次还给同学5元；有的“拼钱买”，付10元和付5元的两个学生平均分着吃。钱又该怎么还呢？同样引发了学生的思考。这个问题来自学生的真实生活，又很有思维深度。回到学校后，教师紧紧抓住契机，与学生们一起进行探讨。

15元分成一样多的两份，虽然学生没有学过除法，但是可以借助学具钱来进行操作。先换钱，把一张10元换成两张5元，一张5元换成五张1元。两张是双数，可以分成两个一半；五张是单数，不能分成两个一半，拿出其中的一张1元继续换钱，一张1元可以换成两张5角。现在5元、1元、5角的张数都是双数，都能分成两个一半了。在操作中，学生们经历了换钱，调用了单双数知识，弄清了每人吃了价值7元5角的爆米花。最后进行单位换算和计算，解决了该还多少钱的问题。这样的实践作业，既解决了真实的生活问题，又提升了学生的问题解决能力和数学思维水平。

图2

（三）关注热点，设计时政性作业

每一门学科都承载着育人功能，数学作为基础教育中的一门重要学科，不但要使学生掌握最基础的数学知识，重视发展智力、培养能力，还要结合学科特点对学生进行潜移默化的思想品德的教育。在设计数学作业时，教师可以结合社会热点设计一些时政性作业，帮助学生逐渐形成关心国家大事、关注社会热点的意识。

例如，结合社会热点“孟晚舟事件”设计数学作业，有的学生通过调查收集数据，计算出孟晚舟从2018年12月1日在加拿大温哥华被拘留到2021年9月25日回到祖国的怀抱经历的天数；有的学生根据此事件的进展画出时间轴；有的学生用手抄报的形式展示自己的研究和想法。不管哪一种方式，学生都在完成作业的过程中了解到该事件背后的政治原因，激发了爱国情怀。

二、分层设计内容，满足不同需求

（一）课时作业层级设置，激发挑战欲望

每节数学课之后都会有配套的课时作业，如果采用一刀切的方式，学生都做同样的内容，就会出现学优生吃不饱、学困生吃不了的现象。因此，教师可以根据学生学业水平层次，优化作业结构，设置“三星”层级作业，这样既能充分激发学生的挑战欲望，又能实现“减负增效”的效果。

课时作业分为一星基础题、二星提升题、三星拓展题。基础题是每个学生都要做的作业，可以达成巩固基本知识和形成基本技能的目标。提升题以变式练习和综合应用为主，是大部分学生可以做的作业，旨在提升学生思维水平，掌握灵活解题的方法。拓展题需要多角度分析思考，答案可能多样化，学生根据个人的实际情况选择做或者不做，也可以跟小伙伴讨论之后再完成。

（二）假期作业套餐组合，保持作业兴趣

每到假期，各年级的数学作业可以进行整合，设计成作业“套餐”模式，供学生自由选择。学生可以在“套餐”中挑选适合自己“口味”的作业。

比如，长假作业可以设置“习惯养成”套餐、“实践体验”套餐、“欢乐学习”套餐，每一个套餐中再设置若干个小栏目。“习惯养成”套餐可以设置每日数学阅读、体育运动中的数学等内容，一静一动，相得益彰；“实践体验”套餐可以设置实际测量、综合与实践等内容，动手、动口、动脑，提高学生的综合素养。合情合理的作业分层，给学生提供了选择的权利，有选择权就意味着“作业主动”，也就意味着更多的“参与性”。当学生根据自己的兴趣和能力去写作业时，作业就不是负担，而是一种快乐的学习活动。

三、凸显作业过程，突出数学思考

（一）设计说理表达型作业

传统的数学作业，习题出现在作业本上，学生单一做题，教师批改的时候往往只关注学生做得对不对。长此以往，学生头脑中留下的只有一个结果，而对知识的形成过程很少关注。说理表达型作业则能变静为动，充分调动学生的思维，让思考有迹可循。

比如：把84-49设计成一道选择题，需要设置A、B、C、D四个选项。

图3

（1）请你算一算84-49的结果是多少。

（2）如果35放在选项B，那么选项A会是多少，为什么？

（3）请你继续给选项C和选项D设计错误答案，你是怎么想的？

选择题中的每一个选项是精心设计的结果，正确答案以外的其他选项都带有一定的迷惑性。让学生设计四个选项，除了其中一个正确选项“35”之外，其他的错误选项都要基于一定的理由进行设置。有的是个位不够减，倒过来用9减4得到错误选项“45”；有的是减法算成加法，得到错误选项“133”；有的是14减9算错，得到错误选项“36”；等等。这样的作业，充分体现出学生的思考过程，而不仅仅是一个结果。

再如：有两根绳子，第一根长39米，第二根长21米，把两根绳子系在一起大约长多少米？设置A、B、C三个选项，并说明理由。

给这道题设置选项，除了要考虑两根绳子的长度之外，还要联系生活经验，考虑打结的长度。所以，其中一个正确选项设定为比60米短一点，另外两个错误答案则可以正好是60米和比60米长一点（A.60米 B.59米 C.61米）。学生经常做这样的说理表达型作业，以后做选择题时，就会去理解每一个选项背后的原因，从而进一步深刻理解数学知识。

（二）设计深度探究型作业

纪德曾说过：借芦苇的摆动我们才认识风，但风还是比芦苇更重要。数学的现象和本质就好比芦苇与风的关系，数学教学始终应该更多关注数学的本质。深度探究型作业可以引导学生透过数学现象去探究数学的本质。

例如，在学习完“平行四边形的面积”一课后，教师可以设计一次深度探究型作业。“有限可加性”是图形计量的重要原理之一，以长度为例，用米尺测量黑板的长度，不能一次性测出结果，这时可以分成几次测量，每次测量时相互衔接又不重叠。那么，黑板的长度就是几次测量相加的结果。平行四边形面积也可以分成几次进行测量，关键是找到合理的分法。教师可以如下操作：

（1）观察现象：教师用一沓A4纸演示下面的过程，学生观察到这沓纸的侧面原来是长方形，后来变成了近似的平行四边形，但是面积没有发生变化。

图4

（2）深度探究：你能根据这一现象用不同的方法探究平行四边形的面积计算方法吗？请你利用画图和说明的方法展示探究过程。

学生在观察中得到启发，把大平行四边形平均分成若干个小平行四边形，然后将分成的图形剪开，位置微移拼一拼，拼成一个近似的长方形。如果把大平行四边形平均分成16个、32个、64个……小平行四边形，那么当分成的个数无限多时，拼成的图形就变成了长方形。平行四边形的底就是长方形的宽，平行四边形的高就是长方形的长，因为长方形的面积＝长×宽，所以平行四边形的面积＝底×高。

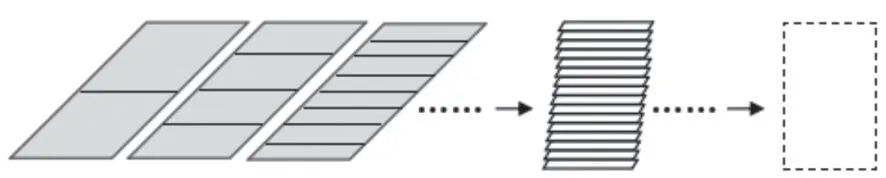
图5

在上述作业中，学生透过数学现象洞悉数学本质，从不同的视角探究平行四边形的面积计算公式。探究过程展开充分，综合运用画图、动手操作、说理等学习方式；探究结果富有内涵，初步渗透了极限思想，培养了学生的数学核心素养。

总之，数学作业设计要摒弃难、繁、偏、旧的弊端，以批判性思维继承与发扬传统数学作业的优点， 以创新性思维优化和创设最合适的数学作业。教师要在作业的形式、内容、过程设计等方面进行综合探究，不仅要落实作业“减负”，而且要探究作业“提质”，让一份份优秀作业成为学生自主学习和主动成长的“跳板”，让作业成为学生在数学学习中最美好和快乐的体验。