抓住图形联系，构建认知模型——《看图解决问题》教学片段与思考

江苏省南京市生态科技岛小学 朱 蓉

看图列式是数学教学中的一个重难点，也是一年级学生涉猎解决问题的敲门砖。它是利用数形结合、“分与合”的互逆关系来解决实际中的数学问题。因此，教师在教学过程中要为学生打好“分与合”相关知识的基础，帮助学生把握好“分与合”的关联，激活学生已有经验，归纳解决问题的方法，实现知识的有效迁移。

一、教学再现

如何以学生更容易理解的方式来教学这部分内容？笔者在教学这部分内容时，重点围绕构建“品字图”模型、体会加减法的意义（“分与合”）、重构“看图列式”模型、体会“分与合”之间的数量关系这几个方面进行。

（一）利用“品字图”模型复习看图列式

片段1：提取“品字图”模型

1.用加法进行分与合

师:你从图上看到了什么？

生：原来有2只小鸟，又飞来3只，一共有5只鸟。

师：你能在品字图上写一写、说一说吗？

生：因为2和3可以合成5，所以2+3=5。

2.用减法进行分与合

师：你从图上看到了什么？

生：原来有3只青蛙，跳进河里1只，荷叶上还剩2只。

师：你能借助品字图边写边说吗？试试看。

师：小朋友们，刚刚我们解决加减法问题时都用到了什么？

生：品字图。

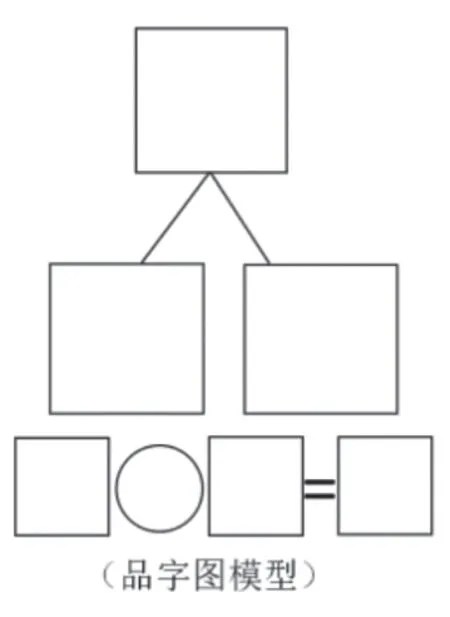
师：今天我们继续借助品字图来学习新的知识。

【教学说明：“品字图”模型是笔者在教学“分与合”部分内容时就给学生练习的图示模型，学生经过一个单元的练习，对“求合”用加法、“求分”用减法已经掌握。通过复习加法和减法问题，唤起学生对“分与合”的相关知识经验，从而从加减法看图列式中提取出“品字图”模型，帮助学生迁移到接下来要学习的新知识中。】

（二）利用“品字图”模型进行表征

片段2：探究加法问题，感受“合”

出示情景图。

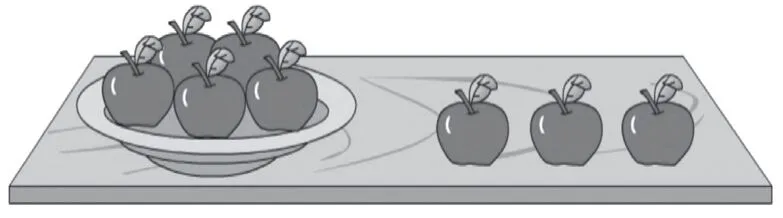
师：你从图上看到了什么？

生：盘里有5个苹果，盘外有3个苹果。

师：你能提出用加法计算的问题吗？

生：一共有多少个苹果？

师：你能把这三句话连起来说一说吗？（个别说，同桌说）

师：“盘里有5个苹果，盘外有3个苹果”这是我们知道的，在数学上我们把它叫作条件。“一共有多少个苹果”这是我们不知道的，也就是要求的，我们把它叫作问题。

师：现在看着这三句话，请你说说条件是什么，问题是什么。（个别说，同桌说）

师：根据这两个条件我们可以求出这个问题，你能在“品字图”中表示它们的关系吗？

【教学说明：第二层次仍然利用“品字图”来解决加法问题，学生通过用“品字图”来表征题目中各个条件的关系，从形式上看，让学生初步感知到这种问题可以用“品字图”来表征；从内容上看，这部分转化为用“品字图”来解决的问题学生已经非常熟练，通过“品字图”的巩固练习，自然而然为接下来引出“括线图”打下了基础。】

（三）建立“括线图”模型

片段3：“品字图”巧变“括线图”

师：同学们，我们是借助“品字图”来解决这个问题的，今天我们要学习另外一种表示方法来帮助我们解决问题。

师：看，这个符号在数学上叫作括线，你能和老师一起用手势比画一下吗？这里的括线表示什么意思呢？

（出示上文中的情景图）

生：表示把盘里和盘外的苹果合起来。

师：括线下的问号表示什么呢？

生：表示问题，要求一共有几个。

师：比较一下这两幅图，它们有什么相同和不同之处呢？

出示对比图：

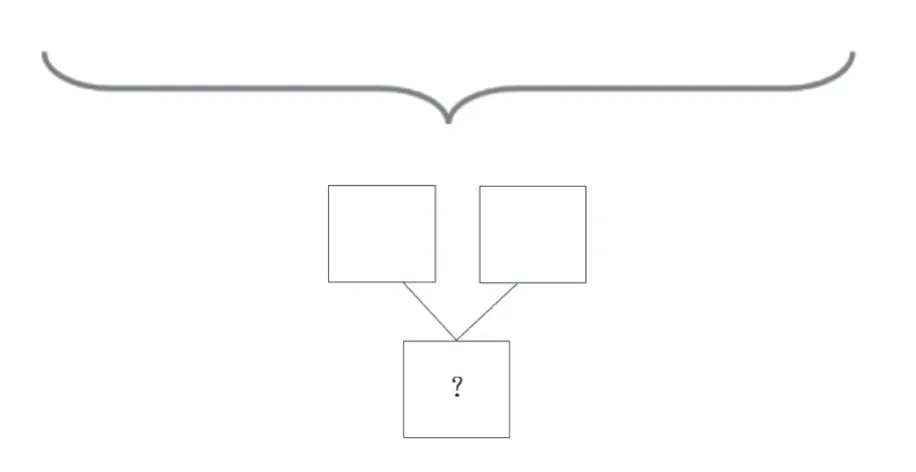
生：都表示分与合的关系。不同的是“品字图”是连线，“括线图”是括线，但括线和连线都表示把它们连起来。

师：说得真好。我们能把这两幅图合起来吗？你想怎么合？

出示“括线图”：

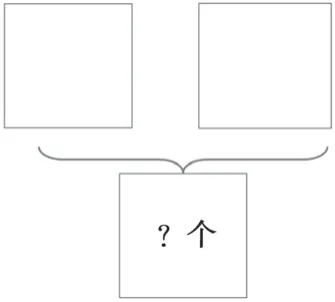
师：其实“品字图”就是“括线图”，“括线图”就是“品字图”，只是连线变成了括线。不管是“品字图”还是“括线图”，这里都表示分与合。在加法问题和减法问题中，这里的分就是部分，这里的合就是总数。

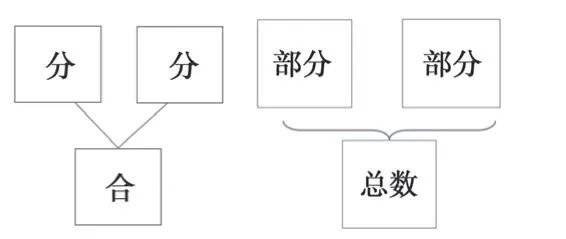
【教学说明：学生有“品字图”模型的经验，于是教师向学生演示5个苹果可以用数字5来表示，3个苹果可以用数字3来表示，再用方框框起来或用括线括起来，学生能很清楚地看出“品字图”和“括线图”其实就是一种模型图，只是连线不同。接着，让学生观察“品字图”和“括线图”的异同，就自然而然地将新知和旧知进行了衔接，让学生对 “括线图”的理解变得容易了许多。】

（四）探索减法问题，感受“分”

师：同学们，刚才我们借助括线图解决了加法问题，同样地我们也可以借助括线图来解决减法问题。

……

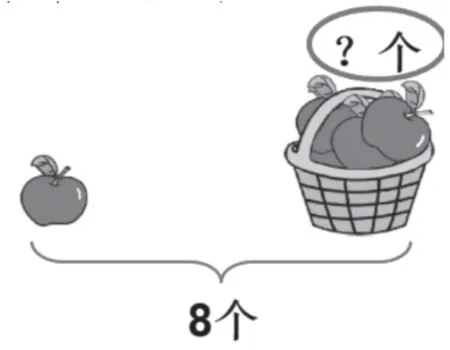
（五）整理分类，总结提炼

师：转眼间我们解决了许多题目，老师把它们全部整理出来了，你能把它们分分类吗？你觉得可以分成哪两类呢？

生：加法和减法。

师：其实用加法计算就是在求总数，用减法计算就是再求部分数。老师现在想请小朋友上台分一分。

出示分类小游戏。（图略）

师：通过刚刚的分类游戏，我们发现了求总数的时候，要用加法计算；求部分数的时候，要用减法计算。

【教学说明：在教学实践过程中，笔者有意识地运用分类整理的方法，引导学生通过分类和整理，观察分类结果和整理出的成果。在教学过程中，学生能够有根据、有条理地运用数学语言表达出自己的思考过程：求总数的时候，要用加法计算；求部分数的时候，要用减法计算。因此，在教学过程中重视对知识点的分类整理与总结归纳，能够充分发挥学生学习的主体性，提高教学的实效性，同时也有助于学生形成有序、完整的思维模式，促进低年级学生合情推理能力的发展。】

二、教学思考

数学课程标准指出：“要培养学生直接从图中搜集、分析和处理信息的能力。”学生看图、分析和处理图中信息的能力对加减法意义的理解有一定关系。怎样才能让一年级学生从图文结合的情境中获取有用的数学信息、准确地看懂图意、列出正确算式呢？笔者认为可以从以下五个方面培养学生“看图列式”的读题和解题能力。

（一）是“联”

“看图列式”这部分教学内容与学生之前学习的“分与合”是相互联系的。通过联系学习“分与合”时使用的“品字图”模型帮助学生回忆之前用“分与合”来解决的加减法问题，为学生更好地理解用“括线图”解决看图列式打下了基础。

（二）是“看”

“看图列式”首先要会看图，教师在教学时要指导学生学会看图，看清楚图中有哪些有效信息、给了哪些条件、提出了怎样的问题，包括看清图中的数字、文字以及括线、问号等的位置。不容忽视的是，为了帮助一年级学生养成会看图、细看图的好习惯，教师在日常教学中应该指导学生把图中的条件圈出来，将图中物体的数量标在图上，同时要也把问号的位置圈出来，这样更有利于学生理解在什么情况下是求总数、在什么情况下是求部分。所以说，学会看图是看图解决问题的前提条件。

（三）是“说”

在学生看图后，能用准确简洁的语言说清图意显得尤为重要。在教学中，“已知一共有（总数），左边有（部分），要求右边有几个（部分）”的这句话可以帮助学生更好地理解求部分用减法计算；而“已知左边有（部分），右边有（部分），要求一共有几个（总数）”这句话则可引导学生求总数用加法计算。学生会说图意，那么就真正理解题意了。

（四）是“用”

建构主义告诉我们，学生主动地建构知识的意义，是无法由他人来代替的，比起生硬的灌输，学生更需要也更喜欢经历知识的形成过程。在教学中，笔者通过借助一些“模型”让学生自己修改，则更容易加深学生对题目的印象。从教育心理学的角度看，操作学具是在增强学生的感知觉，促使零散的感性认知向系统的结构化认知发展，最后上升为数学思维。所以，数学学具的教学价值不仅在于它能帮助学生建立表象，更在于它能促进学生数学思维的发展。

在本节课中，一方面笔者联系之前建构的“品字图”模型帮助学生回顾之前“分与合”加减法的问题；另一方面通过比较“品字图”与“括线图”的异同，让学生明确“括线图”只是“品字图”的另一种表现形式，帮助学生将使用“品字图”的经验转化到“括线图”上。这样，使原来生硬难懂的新符号变得更容易接受了。

（五）是“理”

看图解决问题的出题类型有很多种，通过变化括线和问号的位置，一道新的题目就产生了。

首先，教师出示常见的加法括线题和减法括线题，有意识地指导学生运用分类整理的方法，让学生自己分类并整理出两类题型的特征：用加法计算的题目都是在求总数，问号都在括线的下面；用减法计算的题目都是在求部分，问号都在括线的上面。通过分类整理，学生能够有根据、有条理地运用数学语言表达出自己的思考过程：求总数的时候，要用加法计算；求部分数的时候，要用减法计算。

其次，当学生明确括线题的两种基本类型后，教师拓展左括线图、上括线图、右括线图，学生通过推理经验，总结归纳出做题的方法后，理解此类题型就容易得多。

最后，在练习设计时，教师重视设计一些由易到难的对比试题，提高学生解决问题的能力。在不断地对比训练中，培养学生收集整理信息的能力，让学生自主寻求解决问题的方法。

总之，教师在教学中，一方面要引领学生经历加减法（分与合）的意义的建构过程，激活学生已有经验；另一方面要重视让学生经历整理的过程，归纳解决问题的方法，帮助学生形成有序、完整的思维模式，促进其合情推理能力的发展，从而实现知识的有效迁移。