整体把握数学教材 发展学生思维张力
——“小数的意义”教学实践与思考
2022-04-21江苏省苏州相城实验小学校陈忆雯
江苏省苏州相城实验小学校 陈忆雯
毕达哥拉斯说:“数支配着宇宙。”数的认识是学习数学的基石。“小数的意义”是“数的认识”的一节种子课。理解数的意义、进行数的认识的教学研究,需要教师基于学生的数学学科核心素养,采用有效的策略与方法引导学生去探索、思考与理解数的内容本质,发掘其中体现的数学思想,以便培养学生的数学学科素养。笔者针对“小数”进行了大量的文献研究,并在教学实践中多次进行“小数的意义”的对比教学,发现生活中处处都有小数,但学生对于小数意义的理解存在一定困难。本文以“小数的意义”为例,从厘清概念、把握教材和研究数系三个角度,浅谈如何整体把握“小数的意义”的教学,同时发展学生的思维张力。
一、厘清概念,分析现状
(一)研究学生
从目前的教学现状来看,多数学生认为有小数点的数就是小数,或者比1 小的数就是“小数”。这是源于关于小数的概念,教材上给出的定义是“我们可以把分母是10、100、1000 的分数写成一位小数、两位小数、三位小数……”,这句话指出小数是十进制分数的一种特殊形式。把十分之几界定为小数的意义,并不能让学生从本质上去理解小数,学生的理解在课堂上没有得到正确的解释,因此出现了概念模糊的情况。
(二)研究概念
教师首先需要厘清概念。人们对数的认识是源于远古时期“结绳计数”所产生的自然数,自然数是对整数数量的抽象理解。但是后来人们在生产生活中遇到了当测量小于单位“1”的量时,自然数已经无法满足生产生活的需要,分数和小数也由此产生。比如:1 厘米写成多少分米,用小数来表示就是0.1 分米。从这一点来说,小数的教学重点和概念本质应该是用来表示小于单位“1”的数。
(三)研究教学
结合实际教学,对于小数概念的认识,教师不能只是满足于教学小数的书写、组成和小数与分数的转化等,而是需要思考一些更为本源的问题。例如,生活中已经有整数了,为什么还会出现小数?要把构建“小数”背后的数学思想方法用学生易懂的方式表达出来。
二、梳理体系,构建联系
(一)数的体系的关联性
研究小数的意义首先需要研究数的体系。笔者结合整个小学阶段“数的认识”的结构,进一步整理了整数、小数和分数的关系模式图(见图1)。小数的学习是在学生学习了整数和分数的基础上展开的,学生对数的认识是从最基本的整数开始慢慢扩展的。因此,教师要把分数和整数、小数和整数联系起来教学,否则学生就会觉得小数是全新的,与以往学过的知识没有关系。
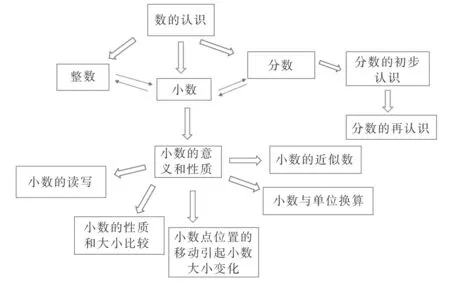
图1
小数的本源是数,教师需要迁移学生已有的知识经验,将小数与整数、分数进行连接,让学生感悟到数的体系内在的统一性,以便引导学生追溯小数的本源,感悟数的统一性。
(二)位置值的统一性
通过位置值将小数和整数联系在一起。可以借助1和0.1 的关系为突破口(见图2),把十分为10 份,得到1,1 再接着平均分10 份,每份就是0.1。从位值制来看,个位不够再往下分,需要创造新的数位,个位的右边就出现了十分位,学生熟悉的100、10、1 和新认识的0.1、0.01、0.001 就产生了联系。反过来看,10 个0.1 是1,10 个1是10……与整数的十进制也是相同的。小数和整数正是通过十进制而连接起来了,最直观的体现就是计数器上从整数数位到小数数位的统一性。为了突破这个教学难点,教师可以利用正方体或者数轴,清楚地向学生解释两者之间的关系。
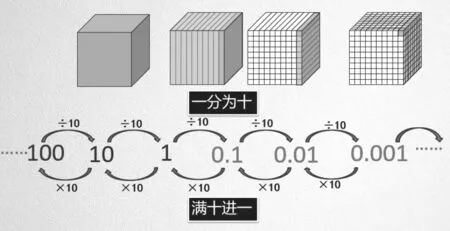
图2
(三)数与生活的密切性
将小数回归于生活,就能解释小数和分数的关系。一是小数和分数之间的联系,小数是分母为10、100、1000……的分数的另一种形式;二是两者之间的区别,这一点与生活是密切相关的。关于生活中人民币的使用,如果都用分数,在付钱和找零时会比较麻烦。为了更加方便生活,也为了方便计算,就出现了和整数的位值计数以及算理都比较一致的小数。
三、研读教材,优化策略
为了更好地把握“数的认识”的教学,教师需要研读教材,抓住教学内容的重难点,分析教材的编排意图。笔者在研究小数概念内容的基础上,分析不同版本的教材,总结出以下三个关键教学策略:
(一)依托经验,引发认知需求
著名数学家兼心理学家斯根普认为,数学概念的教学有基本原则:超过个人已有概念层次的高阶概念不能用定义方式来沟通,只能搜集有关例子供其经验,再靠他自己抽象以形成概念。
有了整数,为什么还需要小数?为了解决这个问题,笔者深入研究了教学内容,对比分析多版本教材的优势,发现数来源于生活,小数的产生是因为生活的需要。在教学中,教师可以借助生活情境引发小数产生的需求。
例如,人教版数学教材设计了贴近生活的问题情境(见图3):用尺子去测量讲台的长度是1 米多一点,但是又不到2 米,用米做单位多出的部分不够1 米。学生已有的知识无法解决这个问题,认知产生了冲突,不能得到一个整数的结果,自然引发了小数产生的需求。

图3
基于以上分析,笔者在教学中对于小数的引出是通过设计实际的生活情境:测量同学的身高。(见图4)
【片段1】
师:这名同学的身高是多少米呢?
(学生有点犹豫)
师:能用1.4 米表示吗?
生:不能。
师:能用1.5 米表示吗?
生:也不能。

图4
师:现在用这把尺子能否准确量出他的身高呢?
生:不能。
师:一位小数不能表示这名同学的身高,谁能帮忙改进一下?
生:将这一格再分一分(将0.1 米再细分单位成0.01 米)。
师:怎么分?
生:平均分成10 份。
师:把0.1 米也就是1 分米平均分成10 份,每份是多少?
师:用小数表示就是0.01 米。
从生活出发,通过创设测量学生身高的情境自然而然地引出了小数产生的需求,引发了学生的认知冲突,推进了学生主动思考。这样的情境设计,没有刻意地标示课题,但无形中已经在学生心中播下学习小数的种子了。测量身高的过程更是体现出了小数的本质:由于生活中整数无法满足需求,需要单位的再细分,从而产生更小的计数单位,引出两位小数的认识。学生学习的种子会生根发芽,思维也潜移默化地影响着他们。
(二)丰富表征,呈现多维视角
华罗庚教授曾说:“数无形时少直觉,形少数时难入微,数与形,本是相倚依,焉能分作两边飞。”数学课程标准强调,“数学课程能使学生掌握必备的基础知识和基本技能,培养学生的抽象思维”。完善小数的意义,要让学生经历小数从生活中来,再借助图形表示数形结合的过程。分析各版本数学教材,其对于小数的表征方式,都采用了从生活到图形,再到抽象的数的方式。从尺子或者钱币出发,引出小数的认识,再借助图形,用正方形表示一位小数和两位小数,最后由面到体,用正方体来表示三位小数。这样一种从具体到抽象的过程,从平面图形到立体图形的多维递进,使得学生对小数的认识更加具有层次性。比如:一维的正方形,可以解决学生理解0.1 和0.01 这一教学难点。教学设计如下:
【片段2】
师:最左边这一条(见图5)是把正方形平均分成10份,那每份是多少?
生:0.1。
师:第2 条这一小格通过量一量发现也是平均分成10 份,每份还是0.1 吗?
生:不是,是0.01。
师:都是平均分成10 份,这里为什么是0.01?
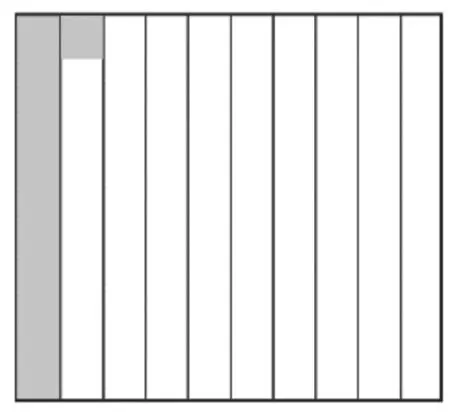
图5
生:因为0.1 是把正方形平均分成10 份,0.01 是把0.1 平均分成10 份。
小数的教学是数的教学,将小数的意义从生活实物再到图形中的面积关系和体积关系,是一个数形结合的过程。0.1 的意义不能局限于生活中的物体,借助几何可以更加清楚完整地描述小数的意义,0.1 不仅存在于长度中、人民币中,也存在于面积中、体积中……这样小数意义的构建才是逐步完整的。
以上片段的教学设计不仅体现了几何直观的数学素养,也渗透了推理能力的培养。让学生由如何得到0.1推理出0.01,学生对于小数意义的理解上升了一个台阶。推理能力是数学学习的十大核心概念之一,是数学学习的一种基本思维方式。
(三)借助分数,架构理解桥梁
从小数与分数的关系来说,各版本数学教材都是借用分数作为小数理解的桥梁,并没有直接教学小数,如苏教版数学教材(见图6)。
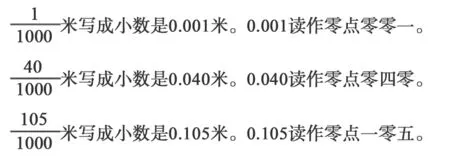
图6
分数与小数是紧密关联的,小数的实质是一种特殊的分数。在概念的理解上,小数和十进制分数应该有对应的关系,比如0.1 和……从学生的角度来分析,小数的认识在分数之后,此时学生已经能够说清分数的意义,在此基础上学习小数的意义更加水到渠成。例如,目前教学中普遍存在的一个问题:教师不能说清楚什么是一位小数、两位小数和三位小数,仅仅是从形式上进行概括,像0.01、0.21 这样的小数点后面是两个数的小数,我们称之为两位小数。其实,理解其本质可以借助分数,因此,笔者在教学中借用分数作为理解小数意义的桥梁。
本课内容的教学,在学生知道0.1 是一位小数的基础上,很容易推理出0.01 是两位小数。学生真的理解两位小数的意义吗?笔者针对这一问题,认为可以在新授完小数后,进行一位小数、两位小数和三位小数的对比总结,借助小数和分数的联系来定义一位小数、两位小数和三位小数(见图7)。
【片段3】
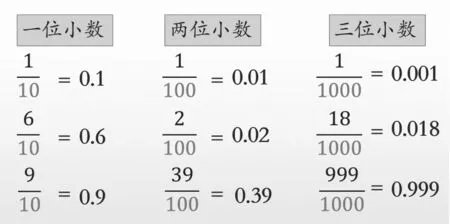
图7
师:0.1、0.6 和0.9 我们知道是一位小数,今天我们学习的是几位小数?第二列都是?
生:两位小数。
师:第三列都是?
生:三位小数。
师:你发现了什么?
生:分母为10 的分数可以写成一位小数,分母为100 的分数可以写成两位小数,分母为1000 的分数可以写成三位小数。
由此,教师巧妙地借助分数和小数的联系对几位小数进行了定义,对比总结出了不同数位的小数和分数的关系。往下再思考,学生还能说出四位小数、五位小数就是分母为10000、100000 的分数……学生对于数的思维的理解从浅层的数形式理解提升了一个台阶:原来小数和分数是有关系的。如此,通过知识的联系提升了学生思维的发散性。
小数的意义是数的认识教学中值得持续研究的主题,有一些可以遵循的规律,还有许多需要探索的问题。小数的认识教学,需要对教材进行整体的研读,把握教学重点,突破教学难点,思考小数的教学的本质,提升学生的数学素养和思维的张力。
