一类Van Der Pol- Duffing 模型的隐藏吸引子存在性问题
2022-04-20聂家升吕小俊
聂家升 焦 岑 吕小俊*
(苏州大学应用技术学院,江苏 苏州 215300)
近年来,随着非线性动力学的发展,复杂动力系统具有多个稳定吸引子共存的特点,称之为多稳态。多稳态现象在各个领域都有发现,如电路系统、生物系统、化学、生态学、气候动力学等,其中Lorenz、Chen 与Chua 等吸引子的研究最为普遍。一些研究还表明,系统对初始值、噪声和控制参数的微小变化极为敏感。因此,控制参数或初始值的微小变化可能会导致共存吸引子的数量和类型发生复杂变化。在多稳态系统中有一种特殊的吸引子,称为隐藏吸引子,它是由Leonov等人发现的,这些吸引子的吸引域不包含平衡点的邻域,并且无法用传统算法寻找它们。Leonov 和Kuznetsov研究了经典的Chua 电路并在该系统中通过一种特殊的分析- 数值算法发现了隐藏吸引子。本文致力于研究非线性动力系统,通过分析- 数值方法寻找隐藏吸引子。
1 Van Der Pol-Duffing 振子模型
2008 年,Matouk 等人研究了一类电路系统,称为自治的Van Der Pol-Duffing振子,他们通过结合Hopf分支理论与数值方法,分析了该系统中存在Hopf 分支与混沌现象,并得到该系统中的一个平衡点分支出了周期轨以及混沌吸引子。2015 年,Dudkowski 等人发现了基于平衡点的Van Der Pol-Duffing振子中存在隐藏吸引子,并描述了平衡点和隐藏吸引子之间的联系。
本文在Leonov和Kuznetsov研究工作的启发下,运用Zhao 研究隐藏吸引子的方法,结合Leonov 改进Chua 系统的思想,考虑一个非线性Van Der Pol-Duffing 振子模型

其中α, β, a,b,c,d 均为系统参数,且均为正。
本文首先根据系统(1)存在的基本特性讨论平衡点的稳定性,然后运用Hopf 分支理论,将α 作为分支参数,计算出系统分支出周期轨的前提条件,并结合分析- 数值方法证明隐藏吸引子的存在性,最后通过数值模拟找到隐藏吸引子。
2 平衡点及Hopf分支
2.1 平衡点及其稳定性
由于α,β,a,b,c,d>0,系统(1)有三个平衡点:O(0,0,0)、P(√[(a-1)/b],0,-c√[b(a-1)]/bd)与Q(-√[(a-1)/b],0,c√[b(a-1)]/bd),其中a >1 且P、Q关于原点对称。
2.1.1 平衡点O的稳定性
平衡点O满足如下特征方程
该式可变为

由上式可知λ1λ2λ3=-αβd(1-a)>0,则方程(2)至少存在一个正根,根据Routh-Hurwitz判据知,平衡点O 不稳定。
2.1.2 平衡点P,Q的稳定性
由于平衡点P,Q关于原点对称,故平衡点P,Q有相同的特征方程
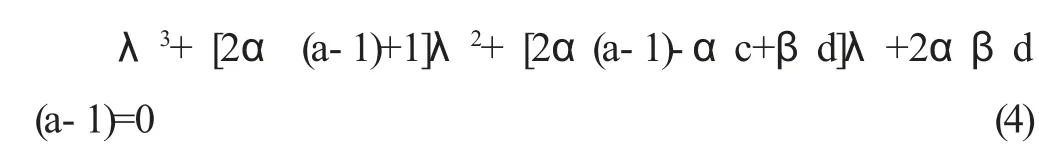
由(3)和(4)式知λ1λ2λ3=-2αβd(a-1)<0,则至少有一个负根,且λ1+λ2+λ3=-[2α(a-1)+1]。
根据Routh-Hurwitz判据可得
定理1:系统(1)的平衡点P,Q 渐进稳定,当且仅当方程(3)的根具有负实部。
引理1:系统(1)出现Hopf分支,当且仅当方程(3)有一个负实根λ=- [2α (a-1)+1] 和一对共轭纯虚根λ2,3=±iω(ω>0)。
2.2 Hopf分支
由于平衡点O不稳定,所以只须讨论平衡点P,Q处的Hopf分支情况。设方程(3)的一个负实根为-[2α(a-1)+1],一对纯虚根为±iω(ω>0)。下面将λ=ωi 代入(3)式,则

分离出实部和虚部,则ω 满足

将α 作为分支参数,则分支临界点αc满足方程

已知α>0,a>1,根据韦达定理,则
(i)若2(a-1)≥c,方程(7)无正根;
(ii)若2(a-1)<c,方程(7)仅有唯一正根

其中Λ= [2 (a-1)-c]2-8βd (a-1)[2 (a-1)-c] 且ω={2αcβd(a-1)/[2αc(a-1)+1]}。
当2(a-1)<c,α=αc时,方程(3)有一对纯虚根±iω,可得
d(Reλ(αc))/dαc={-2(a-1)(βd-ω2)ω2+[2(a-1)-c][2αc(a-1)+1]ω2}/{2ω4+2[2αc(a-1)+1]ω2}.
已知a>1,且由(6)式可得βd-ω2>0。因此若2(a-1)<c,有
d(Reλ(αc))/dαc>0.
由此可得以下结论
定理2: 系统(1)在平衡点P,Q 处出现Hopf 分支,当且仅当α 经过临界值αc,2(a-1) <c 且αc满足(8)式。
3 隐藏吸引子的定位算法
本文运用分析- 数值方法的思想来定位隐藏吸引子。
思考这样一个动力系统

其中P 是n×n 常数矩阵,φ(x) 是一个连续的向量函数,且φ(0)=0。
为了寻找系统(9)的周期解,定义矩阵K 使P0=P+K,有一对纯虚根±iω0(ω0>0),并且其余特征根均有负实部,则上述系统可变为

其中φ(x)=φ(x)-Kx。
引入m+1 个连续函数φ0(x),φ1(x),···,φm(x),使得任意两个相邻的函数φj(x)与φj+1(x)的差别非常微小,这里函数φ0(x)的值很小,并且φm(x)=φ(x)。
由于函数φ0(x)的值很小,可对系统(11)进行谐波线性化,将其转化为

同时确定一个稳定周期解x0(t)。将x0(t)作为初始值,定位系统(9)的吸引子并进行数值计算,增加j 从而得到对应的周期解。此时将出现如下两种情形:
情形一:考虑如下系统

当j=1 时,系统(12)的稳定周期解的吸引域包含周期解x0(t)上的所有点。
情形二:当j=1,系统(11)过渡到系统(12)时,不稳定的分支会破坏周期解。
在情形一的基础上考虑到计算区间[0,T]充分大,将x0(0)看作初始值,运用数值运算找到j=1 时系统(12)的稳定周期解x1(t)。然后考虑j=2 时系统(12)的周期解,将x2(0)=x1(T)作为初始值,得到系统(12)的周期解x2(t)。按此步骤继续运算,将xj(0)=xj-1(T)作为初始值,可以找到系统(12)在j=m时的周期解xj(t),即原系统(10)的周期解。或者在上述运算过程中出现第二种情形,即某一步发生变化导致周期解被不稳定的分支破坏。
下面为了确定初始周期解的初始值x0(0),定义a0的描述函数

定理3:如果可以找到一个正数a0满足
Φ(a0)=0, dΦ(a)/da≠0(a=a0).
那么对于充分小的ε 存在周期解x0(t),它的初始数据满足x0(0)=S(y1(0), y2(0),y3(0))*,其中
y1(0)=a0+O(ε), y2(0)=0, y3(0)=On-2(ε),
并且On-2(ε)是(n-2)维向量,并且
On-2(ε)=(O(ε)…O(ε))T。
接下来根据上述介绍的隐藏吸引子定位算法,运用谐波线性化方法,引入非退化线性变换,获得了系统(1)用于定义初始数据的如下公式

其中a0由(13)式中的Φ(a)所确定,且满足定理3 中的条件。
4 数值模拟
本节取a=1.05,b=0.0001,c=1.25,d=2.05,β=200,进行数值模拟。
4.1 由不稳定的平衡点分支出的吸引子
原系统的三个平衡点分别为:O (0,0,0)、P (10√5,0,-6.0976√5)与Q(-10√5,0,6.0976√5),并且平衡点P,Q 在临界值αc=54.9184 处出现Hopf分支。当α∈(0,αc)时平衡点P,Q稳定,当α>αc时出现更复杂的动力学行为。
结合图1(a)和(b)可知,当α ∈[20,54.9184) 时 最 大Lyapunov 指数均小于0,此时平衡点P,Q 稳定;当α∈(54/9184,58) 时最大Lyapunov指数均为0,此时原系统存在由平衡点P,Q 分支出的周期解;当α∈(58,160] 时最大Lyapunov 指数均小于0,此时原系统随着α 的增加由倍周期分支逐渐变为混沌。

图1 原系统在β=200, a=1.05 时关于参数α 的Lyapunov 指数谱与分支图
4.2 隐藏吸引子
上述数值模拟出的吸引子都是常见的吸引子,下面采用隐藏吸引子的定位算法确定初始值。通过数值模拟可得下图,并且当吸引子是隐藏吸引子时,它们不会起始于平衡点P,Q邻域内的不稳定流形。
当参数α 取不同值时,吸引子存在复杂的动力学行为,平衡点P,Q由稳定变为不稳定,由不稳定平衡点P,Q分别分支出稳定的周期轨,当周期轨破裂后平衡点P,Q周围出现混沌,在这个过程中隐藏吸引子在其周围运动着。图2(a)说明当α=40 时,平衡点P,Q 稳定且隐藏吸引子围绕在其周围;图2(b)说明当α=75 时,不稳定平衡点P,Q 的周围出现了混沌,且隐藏吸引子围绕着这些混沌吸引子。

图2 原系统在β=200, a=1.05 时的相图
5 结论
本文针对非线性Van Der Pol-Duffing 振子模型研究其隐藏吸引子的存在性问题。首先根据Routh-Hurwitz 判据讨论平衡点的稳定性,然后根据经典的动力系统Hopf分支理论,取α 作为分支参数研究原系统的Hopf分支,接着将该系统代入分析- 数值算法中,并在谐波线性化的作用下,得到系统存在隐藏吸引子,最后通过数值模拟证明了原系统存在隐藏吸引子。
