基于EMD 去噪的煤矿井下地质构造声学探测技术

陈亚萍

（兰州资源环境职业技术大学,甘肃 兰州 730022）

从行业发展角度分析,地质构造一直制约煤矿生产发展的核心[1]。在近些年现代化技术不断发展的大环境下,现代化矿井不仅大大提高了掘进速度[2],同时也使得地质构造在开采过程中受到的破坏程度日益加深[3]。面对这一发展现状,以提前预知工作面发展状况为基础的地质构造探测工作就显得尤为重要[4],其也是煤矿开采工作提前做好安全措施[5],快速安全通过危险地质区域的基础之一[6]。关于煤矿井下地质构造的探测研究,文献[7]提出了一种以槽波技术为基础的异常体探测,并以阳泉矿区为目标展开了实际应用测试,探测结果取得了良好的效果,但是部分地质构造相对复杂,受地下水源等因素的干扰作用,其表现出了一定的不稳定性。文献[8]将瞬变电磁法应用到煤层覆岩状态的探测研究中,实现了对水源性特征的准确探测,但是对于地下整体地质构造的分析相对薄弱。声学探测技术作为一种以介质反射特性为基础的地质分析方法,不仅可以实现对复杂地质构成的准确获取同时不受采空区边界的限制,在煤矿井下地质构研究中具有巨大的应用潜力,但是声波中的噪声信息会影响最终的判断结果。对此,提出基于EMD 去噪的煤矿井下地质构造声学探测技术。

1 声学探测信号去噪处理

1.1 声波探测信号EMD 处理

为了实现对煤矿井下地质构造的准确探测,需要对采集到的声波进行去噪处理[9],提高信号的可靠性。以此为基础确保对构造的分析结果与实际结果之间的误差降到最低。为了实现该目标,本文采用EMD（Empirical Mode Decomposition,经验模态分解）方法实现对声波信号的去噪。EMD 去噪的原理是首先对声波探测信号进行小波变换,将其能量分布集中在较小的系数范围内,该范围对应声波探测信号的小波系数表现出良好局部性的区间。同时需要注意的是,这些小波系数只有显著地分布在各个分解尺度上时,最终才能实现对杂波的完整去噪。而地质环境构造中的噪声经过小波变换后,系数分布同样处于细尺度变换的小波域范围内。通过调节分解尺度的大小即可实现对噪声的完全去除。结合该去噪思路,本文利用EMD 对声波探测信号去噪过程共分为3 个实施阶段。

假设采集到的含噪声的声波探测信号为

其中,y 表示含噪声的声波探测信号,x 表示有效声波探测信号,n 表示噪声信号。

首先,对含噪声波探测信号进行小波变换处理,并在该阶段保留最大尺度范围内的低通滤波的系数,需要注意的是,要确保小波系数与真实声波探测信号的变换系数保持一致。针对该问题,本文利用非线性处理的方式对各个尺度下的高通滤波进行统一化处理,将此时得到的系数作为小波变换处理的系数,实现对声波探测信号的转换。对应的小波变换处理的系数计算方式可以表示为：

其中,λ 表示小波变换系数,λ（h）和λ（l）分别表示高通滤波下的波变换系数和低通滤波下的波变换系数,z表示可以执行的最大尺度范围。

在此基础上,利用EMD 根据设定阈值函数对声波探测信号进行去噪处理。

由于煤矿井下地质构造的复杂性以及构成上的多样性,使得矿井下岩体介质的成分、结构和密度等存在明显差异,而这种差异就使得探测声波的传播速度、能量衰减及频谱成分等也表现出对应的差异化特征。利用此,本文将小波变换处理的声波探测信号表示为由多个不同方向上的向量分量构成的分解参数,此时的含噪声的声波探测信号可以表示为：

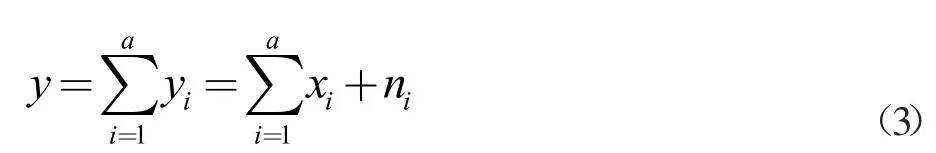
其中,yi,xi,ni分别表示分解后的含噪声的声波探测信号有效声波探测信号和噪声信号。a 表示分解方向数量。由于噪声声波探测信号n 是以正态分布的形式存在的,且不同yi对应ni互不相关,因此ni对应的方差为常量值。结合这一特征,对信号中噪声的去噪处理就可以理解为是对ni的差异化约束。其可以表示为:

其中,W（y）i表示对分解后声波探测信号的小波变换,W-（1y）i表示分解后声波探测信号的小波逆变换运算,u 和分别表示分解后声波探测信号的小波处理结果,Q表示非线性去噪函数,也是实现去噪的核心步骤。

通过式（4）可以看出,要实现对声波探测信号噪声的有效去除,主要依赖于阈值的确定效果。

1.2 阈值自适应设置

为了在声波探测信号去噪过程中更好地保留声波探测信号的有效信息,同时实现对噪声的有效去除,本文建立了阈值函数,通过其计算出最优的阈值范围。在1.1部分已经提到,小波系数需要适应不同尺度上的变换需求,这就意味着阈值也要兼顾不同尺度声波信号的特征。以此为基础,本文设计的阈值函数为

其中,p 表示阈值函数,m 表示尺度参数,通过调节m值的大小,计算出不同尺度条件下对应的阈值。利用式（5）,结合声波探测信号和噪声在不同分解尺度上的能量分布特征,就可以实现对去噪目的。

对于细尺度上的阈值范围,本文以偏硬阈值函数对其进行计算,将其计算结果代入到式（4）中,滤除信号中的大部分噪声。对于宽尺度上的阈值范围,本文以偏软阈值函数对其进行计算,将其计算结果代入到式（4）中,滤除临界区的噪声信号。因此本文建立了以m 调节尺度为目标的数学模型,通过最优化m 值提高式（5）计算结果的自适应性,确保去噪效果的可靠性。具体的数学模型如下：

其中,mj表示m 的数学模型,En和Ej分别表示声波探测信号的能量以及目标声波探测信号能量。按照这样的方式,计算出最优的m 值,并且需要注意的是,对目标声波探测信号能量的设置要以实际矿区地质特征为基础。此时阈值函数从硬到软的变化就可以通过调整m 值由最佳目标声波探测信号能量到允许目标声波探测信号能量实现。

在此基础上,将式(6)代入式(5)即可获得各个尺度上对应的阈值函数,利用得到的结果作为EMD 去噪的基准,实现对声波探测信号的过滤。

2 地质构造探测

在得到去噪后的地质声波探测信号后,就可以根据其表现出的特征实现对区域相应构成的分析和判断。

对煤矿井下地质进行探测所采用的声学探测技术属于主动声纳技术的范畴。通过声纳方程可将传播介质、探测目标和探测设备的作用联结在一起,利用声纳方程建立的关系,能够实现对探测系统性的分析。实际应用中根据不同的系统模型可以建立不同的声纳方程式,对深地层而言,声传播损失和穿透的深度等指标就可以建立地层模型后,通过声纳方程进行大致估算。设置声纳方程式为：

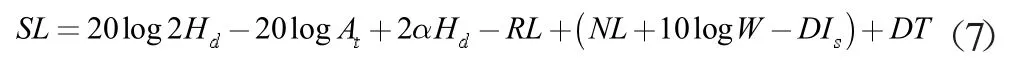
式中,SL 为声源级；Hd为煤矿井下深度(m)；At为透射系数；α 为信号带宽内煤矿井下的平均声衰减（dB/B）;RL为待测界面反射强度（dB）；DT 为检测阈；NL 为信号带宽内平均噪声谱（dB）。

对煤矿井下地质的声波反射与透射产生影响的介质参数有粒径、密度、孔隙度、声速及衰减系数等。根据生源级及计算方程式右边的各参数,可以求出传播损失,进而估算出穿透地层的深度。

基于此分析在探测煤矿井下地质构造时,需要了解声场特性。可以从应用的额角度建立信噪比模型,得出信噪比表达式,得到信噪比简化模型,分析条件：

（1）各地层界面平行时,收发声基阵的声轴都垂直于地面,并具有良好的后辐射抑制能力；

（2）在工作频段内声波对各地层的穿透系数Ati和反射系数Ari为常数；

（3）辐射声脉冲的幅频特性如下式所示,其具有线性相应特性：

（4）接收滤波器的传递函数具有下式幅频特性,且具有线性相位特性：

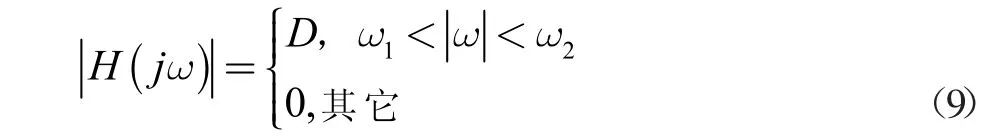
（5）接收声基阵的声电转换函数K(jω)在工作频段内为常数K0；

（6）不考虑延时；

（8）噪声为各向同性、零均值的平稳高斯过程。

在上述环境下,从模型出发得出的最大信噪比的条件为：

式中,cw为声速；S 为发射基阵面积,a 为噪声系数；Ak为待测地面反射系数,HD为地层厚度,Ht为第i 层厚度,βi为第i 层吸收系数。

基于此计算出做基础的地层构成。将声波信号中的高频能量作为各地层的分界,对各个高频能量分量之间的声波进行个性化分析,将其利于已有的岩体特征信号进行对比,拟合度越高,则表明其与对应的地质特征越相似,最后将相似度最高的岩体判定为该地层的岩体构成。

3 实例分析

为了测试本文设计地质构造探测技术的实际应用效果,进行了实际应用分析。

3.1 矿区地质背景介绍

本文进行实例分析具体的参数信息如表1 所示。

表1 测试区域基岩地层构成详细信息

在此基础上,对矿区的覆盖层状态进行统计,发现其主要构成为第四系沉积物,砂粘互生,并伴随有卵砾层不连续发育,下伏地层与之有非密切接触,且整体厚度变化较大,最厚位置可达到750m,最薄位置仅为230m。不仅如此,在测试区域内还伴随有两条明显的断裂,在区域构造应力的作用下,二者分别呈现出东西发展趋势和东南发展趋势。以此为基础,采用本文方法对该区域的地质构造进行探测,并分析其探测结果与实际构成之间的一致性。

3.2 探测结果与分析

采用三种方法对地质构造的探测结果如表2 和表3所示。

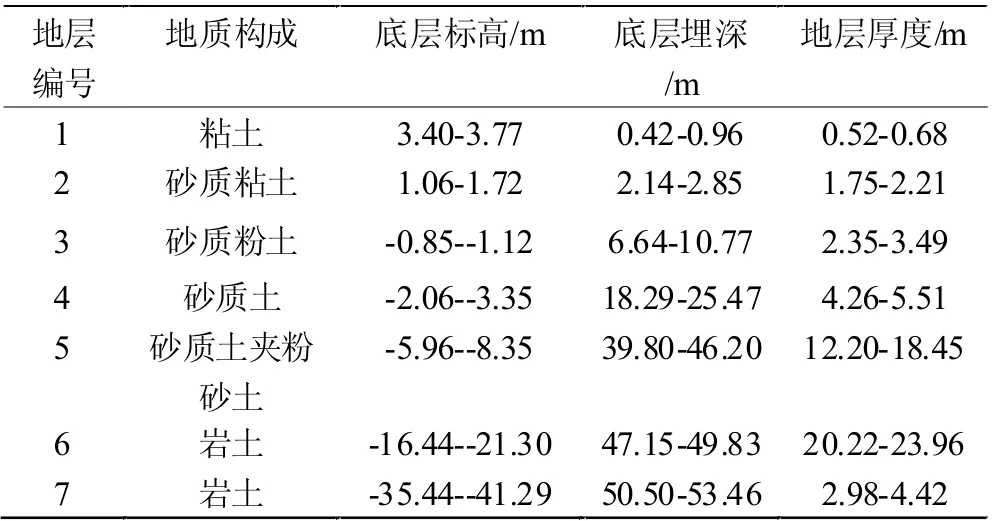
表2 矿区地质构造探测结果

从表2 和表3 中可以看出,本文设计的地质构造探测方法可以实现对地下岩体构成以及成分含量,相关属性参数的获取,对于实际的开采工作具有有效的指导价值。不仅如此,通过观察表2 中的数据可以看出,其最大探测深度为地下53.46m,能够满足大多数矿区的探测需求,对于各地层信息位置以及厚度信息的探测精确到0.01m,可以为开采工作的开展提供可靠的数据支撑。

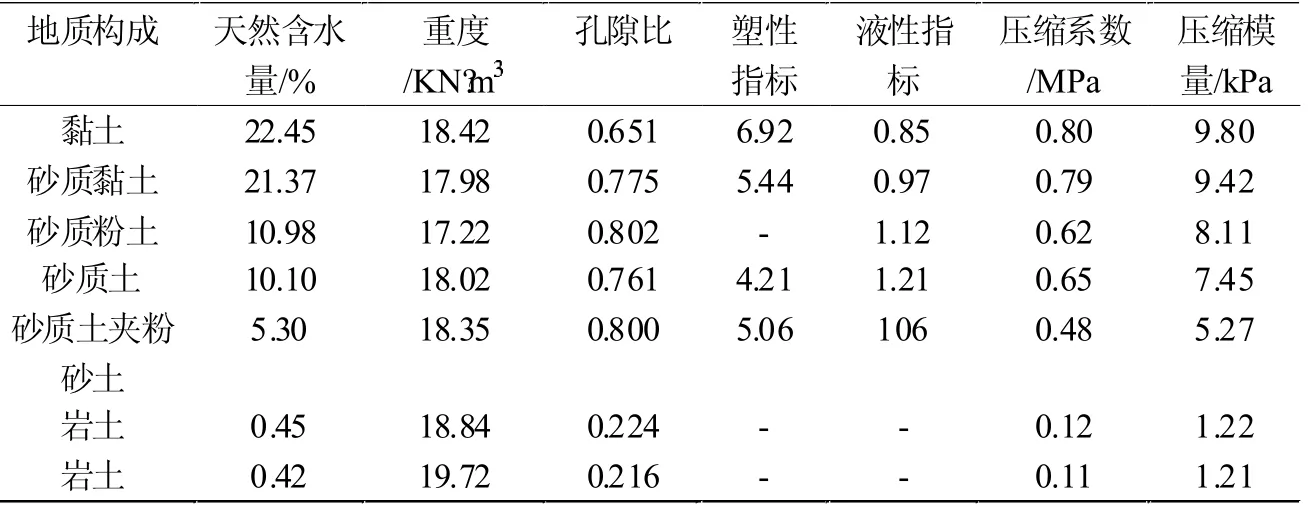
表3 地质构成分析结果

结束语

随着矿产资源需求量的不断增加,对其的探测和开采力度也逐渐增加。不仅如此,在矿井机械化程度不断提高的背景下,如何切实有效地提高煤矿的安全性成为了备受关注的问题之一。除开采技术和开采施工因素外,另一个影响煤矿井下安全的关键因素就是煤矿本身的地质构造,一方面其决定着开采施工的方向,另一方面其也直接决定着相关支护结构的等级要求。本文提出基于EMD 去噪的煤矿井下地质构造声学探测技术研究,实现了对矿区地下构造的准确分析,也希望为相关工作的开展带去帮助。