信号交叉口直右动态车道优化设计及评价分析

梁士栋，陈丽娟，王 影，韩义磊，薄 波

(上海理工大学 管理学院，上海 200093)

0 引言

近年来，随着交通朝着智能化、信息化、动态化的方向发展，动态车道[1]作为提高交叉口通行能力的方法而提出。动态车道是指行车方向按照规定发生周期性变化的机动车道，如：可变导向车道、可变单向车道、潮汐车道等[2]。在动态车道的研究中，孙刚和王丰元[3]对高峰期间采用的可变车道技术进行了研究，研究结果表明该技术可以提高交通效率。 原龙和张勃[4]针对高峰时期交通量严重不均衡的现象，研究了可变车道设计的条件和方法。李丽丽等[5]通过提出一种诱导方法，研究了基于双停车线的布局方法和预信号的配时方法。Brian Wolshon和Laurence Lambert[6]通过强调和总结可逆车道的应用范围，讨论各种可逆车道应用程序如何能够解决问题，尽管没有标准化实践指导实施或保证他们使用的一致性。赵靖等[7]对具有可逆车道的城市主干道进行了综合设计和运营。李灿和赵欣[8]通过建立交叉口可变导向车道控制阈值的综合模型，为后面可变导向车道的控制方法研究提供了参考价值。Khaled J. Assi和Nedal T. Ratrout[9]在研究动态车道分配的问题时，提出了一种快速确定最优车道组的方法。徐洪峰等[10]提出了一种适用于干道沿线信号控制交叉口的复合动态车道管理方法，实现了对城市干道存量空间资源的深度挖掘，可以很好地应对交通负荷大的方向上的周期性变化。马莹莹等[11]提出一种根据双向交通运行状态动态控制可变车道行驶方向的交通控制方法，可以减少潮汐路段的车均延误，缓解道路交通拥堵现状。为了合理配置交叉口空间资源，赵靖等[12]对交叉口的动态车道功能进行了优化，曲昭伟等[13]提出了逆向可变车道的最优分配模型，Wael K.M等[14]将交叉口空间分配优化与信号进行结合，以提高交叉口的灵活性；赵靖等[15]通过对左转待转区的研究，旨在提高左转能力来达到交叉口通行能力提高；李爱增等[16]则是通过借道右转设置提高右转通行能力，从而使交叉口的通行效率提高。

本研究根据动态车道的理念，提出一种新型动态车道控制方法，来解决直右共用车道造成的右转延误增加以及使用效率不足的问题。传统动态车道是根据机动车在不同时段的需求特征变换其行车方向，而本研究提出的新型动态车道控制是将现有的直右共用车道改造成动态车道，再结合预信号理念将可变信息显示板及提前变道标志线设置在距离交叉口的一定位置，并与主信号协调联动。新的动态车道控制，既能减少右转车辆的延误，又能提高交叉口的通行能力。

本研究首先确定动态车道组织设计方案及工作流程，然后在分析动态车道实施中交通流演化过程的基础上，构建信号交叉口处车辆延误计算模型，再分别计算实施动态车道控制前后的延误变化，最后根据实际的数据进行数值分析和评价动态车道控制效果。

1 直右动态车道组织设计

1.1 参数说明

本研究所用的主要参数及其含义如表1所示。

表1 参数说明

续表1

1.2 可变信息显示板的位置

本研究研究的是具有直右共用车道且直行车道不少于1条的信号交叉口，其方向上的进口道存在1个相位和2个相位的情况。

在设有直右共用车道的主路上设置直右动态车道。动态车道上提示变道标志线的作用是：当可变信息显示板由直右变为右转时，机动车驾驶员通过显示板接收信息选择进入左侧直行车道。如图1所示，提示变道标志线的位置应在禁止变换车道线之前，满足其后的车辆变道进入直行车道后能够安全停车。

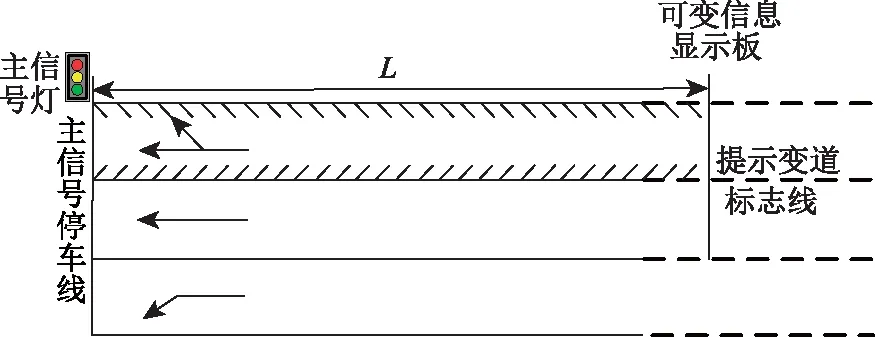
图1 直右动态车道设计示意图

安全停车距离[17]由驾驶员接受可变信息显示板上信息的反应时间内行驶距离、车辆制动距离及车辆停靠时的安全间距组成。而提示变道标志线到停车线的距离L至少满足公式(1)：

(1)

1.3 可变信息显示板与主信号协调控制

可变信息显示板会在主信号变换灯色的前几秒变换信息显示，在主信号变为绿灯的前几秒，显示板变为“直行+右转”，直右动态车道恢复成直右共用车道，此时在提示变道标线后方排队的直行车辆可提前进入直右动态车道；在主信号变为红灯的前几秒，直右动态车道上方的显示板变为“右转”，直右动态车道变为仅允许右转车辆通行，此时行驶在直右动态车道上的直行车辆根据指示及时驶入直行车道，这样就避免主信号红灯时阻碍右转车辆正常通行的情况，从而减小了右转车辆的延误，提高右转运行效率。

可变信息显示板的提前启亮红灯时间应满足两点。[18](1)满足提示变道标线后方的直行车辆能顺利变道至相邻直行车道，并在主信号红灯启亮时安全停在停车线前。(2)满足已经越过提示变道标线的直行车辆在主信号红灯启亮前进入交叉口。因此，红灯提前启亮的时间tr满足式(2)两个约束：

(2)

动态车道指示绿灯提前启亮，在可变信息显示板后方的直行车辆可以选择性的变道至直右车道，保证在主信号绿灯启亮时到达交叉口。因此，提前启亮的绿灯时间tg满足式(3)条件：

(3)

2 车辆延误计算模型构建

2.1 假设条件

为了便于建立延误计算模型，对现实情境中的非关键性参数进行了近似性假设和研究范畴界定，具体内容如下：

(1)交叉口处于非饱和状态，保证每个周期的绿灯结束时，进口道内的排队车辆均能清空。

(2)进口道车辆平均到达率和饱和流率在一定时间内为一确定常数。

(3)不考虑无法换道的情况。

(4)不考虑各个车道上车型比例的影响。

(5)假设只有1个直右共用车道。

2.2 过程描述

提出的动态车道工作流程以及对应交通流运行状态主要分为4个过程。

Case1：直行车辆以到达率qs行驶到交叉口停车线处遇红灯排队形成集结波ws1，如图3中OF所示。此时直右动态车道上的右转车辆处于自由行驶状态。

Case2：在图3点A时刻右转车道上的动态车道指示灯启亮，右转车道升级为直右共用车道。在直行车道排队的部分车辆选择换道至右侧直右车道继续行驶，设此时直行车辆的换道率为α。换道过程中原直行车道波速转变为ws2，即图3中ED段。

Case3：点G时刻换道过程结束，直行和右转车辆均匀分布在直行车道和直右车道上，此时直行车道的集结波发展成为ws3，即图3中DC段。

Case4：当直行的信号绿灯亮起时，排队车辆以饱和流率驶离交叉口，对应的排队消散波为ws，即图3中BC段。

2.3 交通波波速计算模型

由2.2分析可知，每一个状态下的交通波是量化交通流运行的关键参数，因此，为了能够最终计算车辆延误，首先需要对各Case中的交通波进行分析建模。

由经典的交通波计算公式(4)[19]计算各Case下的波速：q和q′为前后两种车流状态的流量；k和k′为前后两种车流状态的密度；Δq和Δk为流量和密度的变化量。

(4)

Case1对应的车流量由q1变为q2，速度由vf变为0，密度由k1变为k2。则波速ws1由公式(5)得到。

(5)

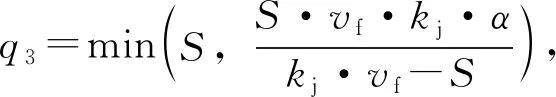
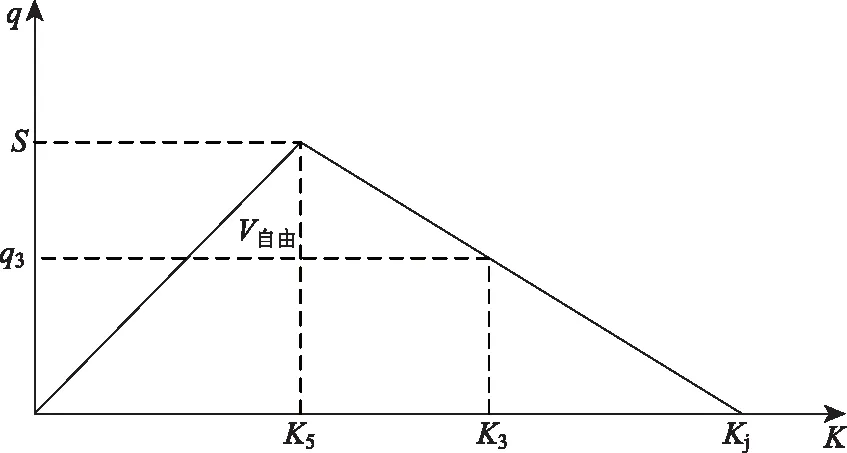
图2 一阶流量-密度关系图

(6)

(7)

Case4对应的车流量q5=S，密度等于饱和流量与车辆自由流速度之比，此时可由公式(8)得到波速ws。

(8)

2.4 车道延误模型

根据上述分析，在交通流稳态输入条件下，如果实施动态车道设置方法，那么在直行车道上的车辆排队情况如图3所示。

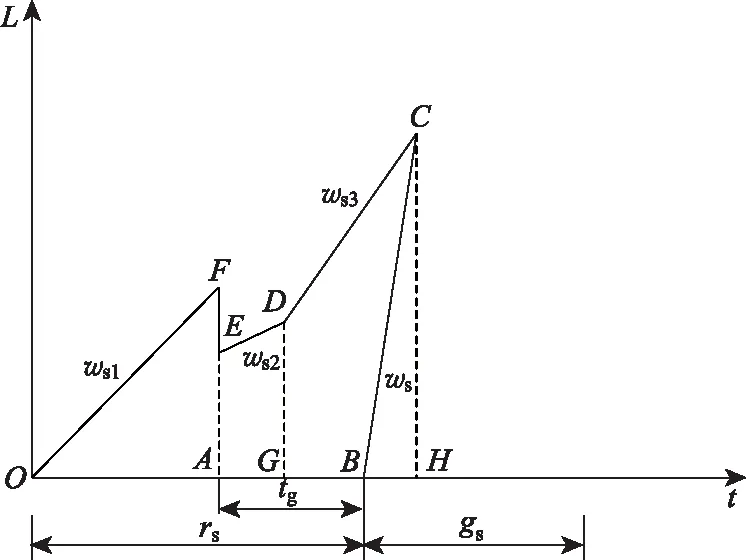
图3 动态车道下直行车道延误

根据车辆延误的物理含义可知，图3中的区域面积为车辆延误，因此求解直行车道的延误就是求解围成的区域面积。由图3中几何关系得到：图中点A，B的横坐标，E，F的坐标由公式(9)计算。

(9)

结合实际的运行过程：直行车道超过禁止换道区Ey的排队长度为Fy-Ey，其中有比例α的车辆选择换道，则剩余车辆为(Fy-Ey)·(1-α)，所以有点D纵坐标的计算公式(10)；又由公式(11)，(12)求得D点横坐标和C点坐标。

Dy=(Fy-Ey)×(1-α)+Ey，

(10)

(11)

(12)

因为△BCD的面积等于BC长度乘上D到BC的距离，由B点坐标和BC斜率推出lBC:ws·x-y-ws·rs=0，所以可以由公式(13)求得SBCD。

(13)

因此，动态车道控制下直行车道的总延误计算公式如(14)所示：

(14)

如果在F点，车辆的最大排队长度小于动态车道长度，则直行车道的车辆不能够换道，此时对应图4。其中FC段对应Case4，其波速为ws3。C点的坐标由公式(15)得出。

图4 无需换道情况下直行车道延误

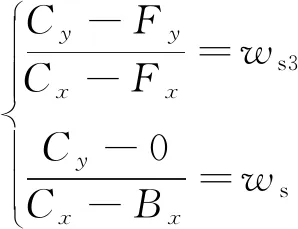
(15)

由公式(16)可以得到直行车道延误为：

(16)

不采取任何措施下直行车道延误约等于直右车道延误，主信号红灯启亮时，直行和右转车辆均匀分布在直行车道和直右车道上，如图5所示：此时直行车道和直右车道的集结波为ws3，对应OA段；当绿灯启亮时，排队车辆以饱和流率驶离交叉口，对应排队的消散波为ws，即图5中BA段。

图5 原直行和直右车道的延误

由图5中的几何关系可以知道B点横坐标和A点坐标由公式(17)和(18)得到：

Bx=rs，

(17)

(18)

所以原直行和直右车道的车辆延误计算公式如(19)所示：

(19)

由于进口道采用直右动态车道的设置对左转车辆基本无影响，因此左转车道的车辆延误计算与原来直行车道车辆延误的方式相同，左转相位红灯期间左转车辆以到达率ql行驶到主信号排队，形成集结波wl；当左转绿灯亮起时，车辆以消散波为ws开始消散。得到公式(20)左转车道的车辆延误。

(20)

在设置直右动态车道之后，提前指示红灯启亮后，直行车辆变道至相邻直行车道，不会阻碍右转车辆通过交叉口，当提前指示灯显示为绿色时，直行车辆在不阻碍右转车辆正常通行的前提下变道至动态直右车道。因此，设置直右动态车道后的右转车辆的延误可以忽略不计。

3 数值分析

为了进一步分析周期长度、饱和流率、换道率、直右流量比等因素对动态车道优化性能的影响，接下来要以这些输入为变量进行分析。受到交叉口交通量的影响，直行相位绿信比可取值为0.35，自由流速度指不受上下游影响的交通流运行速度，可以取值为5～45 km/h，阻塞密度指当所有车辆无法通行，车速和交通量都趋于0时的密度，阻塞密度可以取值为150 veh/km。

3.1 周期长度和饱和流率对车辆的延误分析

将动态车道长度设置为40 m；左转、直行和右转的车辆到达率分别为145，340和100 veh/h，探析在不同的周期长度和饱和流率下延误的改善趋势。

如图6所示，不同曲线代表不同的饱和流率。在饱和流率一定时，延误改善程度随周期的变长先下降后上升，由公式(9)得到当rs≥65 s时，直行车道排队长度大于L，采用公式(14)求直行车道的延误，反之采用公式(16)。因为临界点近似对应图中周期长度为100 s的位置，所以会出现拐点。

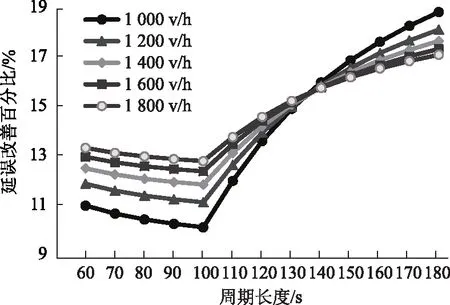
图6 周期长度对延误改善的程度

在拐点左侧，根据公式(16)和(19)计算直行车道延误，其中ws1和ws3不变，S减小使得ws增大，所以采用动态车道后直行车道延误增加的程度变大，延误改善程度变小；又因为直行车辆无法换道，因此随着周期变长，滞留在直行车道的直行车辆产生的延误程度变大，造成延误改善程度下降。

在拐点右侧，随着周期变长，直行车换至直右车道的比例增大，使得直行车道延误增大的程度减小，导致总延误改善程度越来越明显；又因为周期增大，对应的红灯时间变长，在红灯期间排队的车辆数变多，此时在红灯时长相同的情况下，S越大，在绿灯时间通过的最大车辆数越大，延误改善程度的增长速度越缓。

3.2 车辆直行、右转到达比例对车辆延误影响分析

仅探析在不同的直行右转比例下延误随总流量增加的变化趋势。图7包含进口道分别为图(a)3车道和图(b)4车道的情况，其中不同曲线代表不同的直行、右转到达比例。

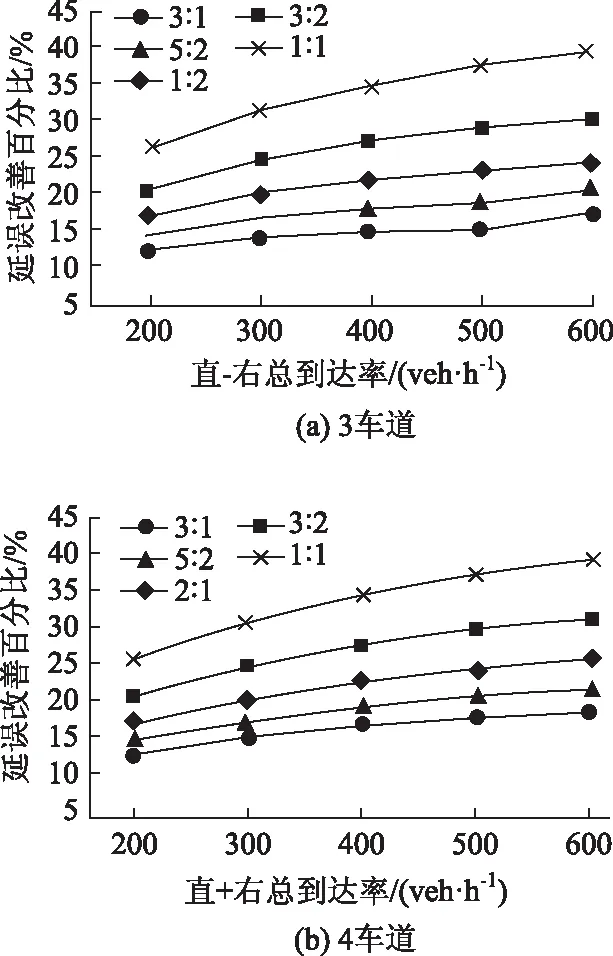
图7 不同直行、右转到达比例下总延误改善程度

如图7所示，直右动态车道在不同进口道条件下的延误改善程度均在10%～40%之间。在总的到达率不变时，随着直行、右转到达比例的增大，延误的改善程度减小，即随着右转车辆的占比增多，车辆的延误改善程度增大。这是因为当主信号变为红灯前，动态车道提前启亮“右转”标志，此时直右共用车道上的直行车辆提前变道至直行车道，直右车道上的右转车辆处于自由行驶状态，从而减少了右转车辆的延误。因此直右动态车道适用于右转车辆占比多的进口道。

3.3 不同自由流速度下对延误的影响分析

设置自由流速度为自变量探寻延误的改善状况。图8为不同自由流速度下延误改善程度。

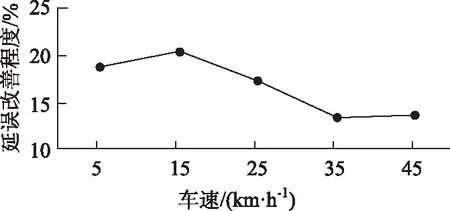
图8 速度对延误的改善程度

由图8可知，当自由流速度位于(5 km/h,15 km/h)时，车速较小，通过设置直右动态车道可以极大减小右转车辆的延误，同时在提示绿灯启亮时缓解直行车道的交通压力，因此此时延误的改善程度是最高的；当自由流速度位于(15 km/h,35 km/h)时，车辆以一个较快的速度到达交叉口，随着车速的增大，延误改善程度不断降低；当自由流速度位于(35 km/h,45 km/h)时，延误改善程度变化不大。在不同自由流速下，设置直右动态车道对延误均有改善，其中当自由流速处于(5 km/h,25 km/h)时延误改善程度是比较高的，因此，可以说明直右动态车道更适用于自由流速度不大的信号交叉口。

3.4 换道率对延误的影响分析

将动态车道长度设置为22 m，根据公式(9)得到当qs≥225 veh/h时用公式(14)计算，所以将总到达率设置为600 veh/h，且满足不同直行右转比例下qs≥225 veh/h。结果得到图9所示不同换道率与延误改善程度的关系，不同曲线代表不同的换道率。

图9 不同直行右转到达率比例下延误改善关系

由图9可以发现，当直行右转到达率之比相同时，随着换道率的增大，延误的改善程度增加。这是因为绿灯提前启亮时，会有部分直行车辆换道至直右车道，如果换道率很小，那么动态车道后方的车辆依旧很多，随着换道率增大，换道至直右车道的直行车辆变多，直行车道延误增大的程度减小，因此总延误的改善程度变大。

4 结论及展望

本研究借鉴预信号以及动态车道的理念，将可变信息显示板与主信号协调联动，提出了一种在直右车道上采用动态车道的形式来减少右转车辆延误的方法。验证结果发现，该方法可以降低进口道以及整个交叉口的车均延误，延误改善程度大致在10%～40%之间。在周期较长、饱和流率较大时，延误改善效果较好。一般周期长流量大都发生在高峰期，因此在高峰期设置动态车道效果更好。本研究的模型和方法不仅能够很好地适应于信号交叉口的交通流运行特性，而且其研究成果可以给相关的工程实践提供一定的理论依据，对城市拥堵难题提供了一定的帮助。但是，本研究也存在很多不足，比如目前模型的一些假设条件过于理想，驾驶员能否在相应的交通流状态下按照预设计完成操作等问题需要进一步研究，后续需要开展更多的研究和调查，这也将作为下一步的研究方向。