落石冲击拦石墙的动力响应模拟研究

2022-04-20吕泽鹏刘红岩

公路交通科技 2022年3期

吕泽鹏，刘红岩

(中国地质大学(北京)工程技术学院，北京 100083)

0 引言

随着我国西部山区基础设施建设的快速发展，崩塌落石灾害发生频率也不断增加，落石灾害已经成为道路交通安全运营的重大隐患。工程中常采用拦石墙进行崩塌落石防治，优点在于能承受极高的冲击动能，受撞击后结构破坏程度低，同时还可存储一定数量的落石，减少落石清理次数，维修成本低，使用寿命长[1]。

冲击力计算是落石防护的核心问题。目前对于落石冲击力的计算，大多数研究是基于3种理论模型发展而来，即Hertz理论模型、能量守恒模型、冲量定理模型，由此衍生出隧道手册法、路基规范法、杨其新法[2]、叶四桥法[3]、瑞士法[4]和日本道路公团法[5]等多种落石冲击力计算公式。由于各种计算方法理论基础和模型假设各有侧重，导致冲击力计算结果有所差异，同一工况下，不同计算方法所得到的冲击力计算结果可能相差6～7倍之多[6]。除此之外，国内外相关学者还对落石冲击力进行了更加广泛深入的研究。王永东等[7]基于Hertz接触理论和JKR黏附理论，得出了落石冲击缓冲层时的冲击力以及坠入深度的解析解。Zhang等[8]根据动量定理推导出了法向冲击力和侵彻深度的计算公式。钟汉清等[9]基于Hertz弹性碰撞理论和Thornton弹塑性假设，推导了落石撞击桥墩的弹性和弹塑性冲击力表达式。袁进科等[10]通过设计的滚石冲击力测试装置进行试验研究，结合常用冲击力计算公式，建立了可用于各影响因素的最大冲击力计算方法。候天兴等[11]基于滚石运动参数并结合冲量定理提出了滚石对建筑物冲击力的计算公式。

除了冲击力的计算，目前国内外对落石冲击拦石墙等支护结构的动力响应问题也进行了大量研究。Plassiard等[12]使用离散单元法研究了落石冲击路堤的动力响应。Ronco等[13]通过建立动态有限元数值模型，研究了落石冲击加筋土堤的动力响应。胡卸文等[14]利用Abaqus有限元软件，研究了桩板墙在落石冲击荷载作用下的动力响应。王南南等[15]利用PFC软件并结合室内试验，研究了落石冲击力在垫层中的扩散规律。江巍等[16]利用PFC软件，比较了3种缓冲材料对落石冲击作用的缓冲效果。罗杰等[17]通过试验验证了SPH-FEM方法在冲击力方面的适用性，并采用SPH-FEM模型分析了落石在4种土壤中的动力响应特征。Mougin等[18]利用试验方法研究了某种钢筋混凝土板在冲击荷载下的动力响应规律。Toe等[19]利用元模型建立了一种评估落石防护屏障有效性的新方法，能够模拟屏障对撞击的响应。

然而目前少有学者较为系统地分析落石因素对拦石墙结构的动力响应规律的影响，尤其是落石因素对拦石墙结构冲击力、冲击变形、拦石墙Mises等效应力3个方面的影响。因此，本研究使用ANSYS/LS-DYAN有限元软件，充分利用数值模拟可研究多种工况的优势，对落石冲击拦石墙结构动力响应问题进行更加系统深入的模拟研究，探究落石速度、质量、角度、形状等4个因素对冲击作用下拦石墙结构的动力响应的影响。

1 拦石墙数值计算模型概述

1.1 有限元模型

本研究选取圬工拦石墙作为拦石墙基本型式，并且依据《地质灾害拦石墙工程设计规范(试行)》[20]中相关规定对拦石墙模型尺寸进行合理的设置，具体尺寸见图1。拦石墙结构主要包括缓冲层和混凝土挡墙。其中，缓冲层采用典型的倾斜式梯形截面，顶部宽度为1 m，底部宽度为4.75 m，坡面坡度为1∶0.75，高为5 m；混凝土挡墙顶部宽度为1 m，底部宽度为1.7 m，墙面坡度为1∶0.1，高为7 m，其中嵌固深度为2 m，露出地面部分为5 m。对缓冲层底部采用法向约束；对混凝土挡墙嵌固段部分采用全约束。由于拦石墙较长，如果严格按照实际情况进行建模，会导致计算量指数级增大，因此本研究只选取其中10 m进行研究。同时为缓解人工截断边界对应力波的反射作用进而影响计算结果，在模型两端采用无反射边界条件，使得计算结果更加精确。

图1 有限元模型尺寸

1.2 材料参数

落石刚度远大于缓冲层刚度，因此可将落石视为刚体模型，其弹性模量、密度和泊松比分别为33 500 MPa，2 260 kg/m3和0.3。根据相关文献[6,21]，缓冲层选取Drucker-Prager模型，其弹性模量、密度、泊松比、内摩擦角和黏聚力分别为35 MPa，1 530 kg/m3，0.37，25°和30 kPa。根据相关文献[6,22-23]，混凝土选取HJC模型，采用C20强度等级，具体参数见表1。

表1 混凝土材料参数

1.3 模型可靠性验证

为验证本研究所建立数值模型的可靠性，首先对本研究建立的数值模型得到的冲击力计算结果和常见的冲击力计算公式得到的结果进行比较。将落石半径固定为0.5 m，此时质量为1 183.33 kg，冲击方向固定为垂直于缓冲层墙面向里，将冲击速度分别设置为5，10，15，20，25 m/s。比较结果如图2所示。冲击力计算结果随冲击速度的增加均近似呈线性增加的变化。每一种计算方法得到的冲击力都有所不同，在相同工况下冲击力计算结果甚至会有5倍以上的差距。这是因为每一种计算方法考虑的因素各有侧重，比如日本道路公团法和瑞士法因为没有考虑缓冲层厚度这一因素，导致计算结果较其他方法偏大。总体上看，本研究建立的数值模型所得到的冲击力计算结果介于瑞士法和叶四桥法之间，计算结果的可靠性可以得到保证。

图2 冲击力计算结果对比

2 落石冲击拦石墙动力响应模拟分析

下面将根据表2所示的4种工况，即落石质量、速度、角度、形状等，研究落石冲击拦石墙的动力响应规律，如挡墙受到的冲击力、冲击变形及拦石墙Mises等效应力等。其中，冲击力指的是落石与缓冲层相互作用的冲击力时程关系曲线，从中可以判断缓冲层所受最大冲击力以及冲击持续时间。冲击变形指的是缓冲层受冲击后表面节点发生的最大位移，可以直观表明撞击的作用效果。经过初步分析，与落石直接接触的点为位移最大点，将其确定为位移监测点。拦石墙Mises等效应力若大于混凝土抗拉强度(1.1 MPa)，则混凝土材料进入塑性状态，开始失效。经过初步分析，Mises等效应力最大值出现在拦石墙体与土体交界处靠缓冲层面中心位置，将该处确定为Mises等效应力监测点。

2.1 不同冲击速度

将冲击速度分别设置为5，10，15，20，25 m/s，其他参数见表2。

表2 数值计算方案

2.1.1 冲击力对比分析

不同冲击速度下冲击力时程曲线如图3所示。

图3 冲击力时程曲线

时程曲线的趋势大致相同，冲击力随时间增长均为先急剧增大后减小至0。冲击速度较大时，时程曲线呈现较明显的脉冲状变化。冲击速度从5 m/s增加到25 m/s时，最大冲击力从164.96 kN增加到1 119.02 kN；冲击持续时间由0.06 s增长至0.167 s。分析表明，落石冲击力和冲击持续时间与落石冲击速度呈正相关。

2.1.2 冲击变形对比分析

不同冲击速度下最大位移时程曲线如图4所示。时程曲线的形状基本相同，最大位移均是在极短时间内近似线性增长至某一最大值，随后产生一部分回弹进而达到稳定状态，这与柏雪松[6]的模拟结果在规律上是相似的。因为缓冲层是弹塑性材料，在大冲击力作用下会产生塑性变形，从而起到吸收冲击能，保护混凝土挡墙结构的作用。冲击速度从5 m/s 增加到25 m/s时，产生的最大位移从0.130 m增加到0.718 m。分析表明，最大位移与落石冲击速度呈正相关。

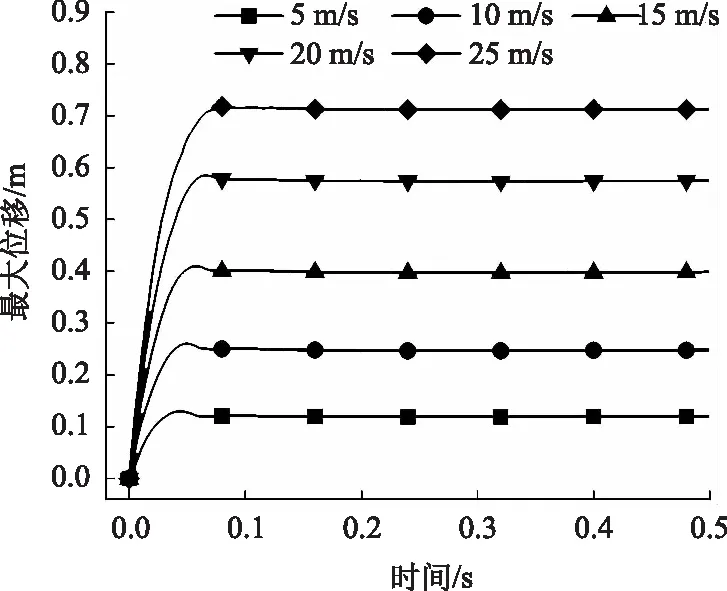
图4 最大位移时程曲线

2.1.3 Mises等效应力对比分析

不同冲击速度下Mises等效应力时程曲线如图5所示。时程曲线的形状基本相同，Mises等效应力随时间增长均为先急剧增大后减小至稳定，且呈现脉冲状变化，速度越大脉冲变化越明显。Mises等效应力在初始一段时间为0，是因为冲击产生的应力波经过缓冲层传递到混凝土挡墙需要一定时间，上述规律与柏雪松[6]的模拟结果在规律上是相似的。冲击速度从5 m/s增加到25 m/s时，Mises等效应力从0.156 MPa增加到0.762 MPa，均未达到混凝土抗拉强度1.1 MPa，拦石墙安全。分析表明，Mises等效应力与落石冲击速度呈正相关。

图5 Mises等效应力时程曲线

2.2 不同落石质量

有2种方法可以改变有限元模型中落石的质量，第1种是固定体积不变，改变落石材料密度；第2种是固定落石材料密度不变，改变落石半径。考虑到在实际情况下，某一地区的岩体密度不会有太大差异，故采用第2种方法。将落石质量分别设置为500，1 000，1 500，2 000 kg，对应的半径别为0.375，0.473，0.541,0.596 m，其他参数见表2。

2.2.1 冲击力对比分析

不同落石质量下冲击力时程曲线如图6所示。时程曲线的趋势基本相同，冲击力随时间增长均为先急剧增大后脉冲状减小，经过一段时间后稳定为0。落石质量从500 kg增加到2 000 kg时，最大冲击力从503.85 kN增加到969.80 kN；冲击持续时间由0.051 s增长至0.118 s。分析表明，落石冲击力、冲击持续时间均与落石质量呈正相关。

图6 冲击力时程曲线

2.2.2 冲击变形对比分析

不同落石质量下最大位移时程曲线如图7所示。时程曲线的形状基本相同，最大位移均是在极短时间内近似线性增长至某一最大值，随后产生一部分回弹进而达到稳定状态。落石质量从500 kg增加到2 000 kg时，产生的最大位移从0.382 m增加到0.723 m。分析表明，最大位移与落石质量呈正相关。

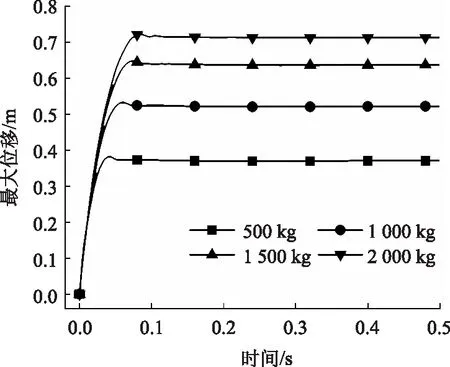
图7 最大位移时程曲线

2.2.3 Mises等效应力对比分析

不同落石质量下Mises等效应力时程曲线如图8所示。时程曲线的形状基本相同，Mises等效应力初始一段时间为0，之后随时间增长均为先急剧增大后减小至稳定，且呈现脉冲状变化。落石质量从500 kg 增加到2 000 kg时，最大Mises等效应力从0.357 MPa增加到0.675 MPa，均未达到混凝土抗拉强度1.1 MPa，拦石墙安全。分析表明，Mises等效应力与落石质量呈正相关。

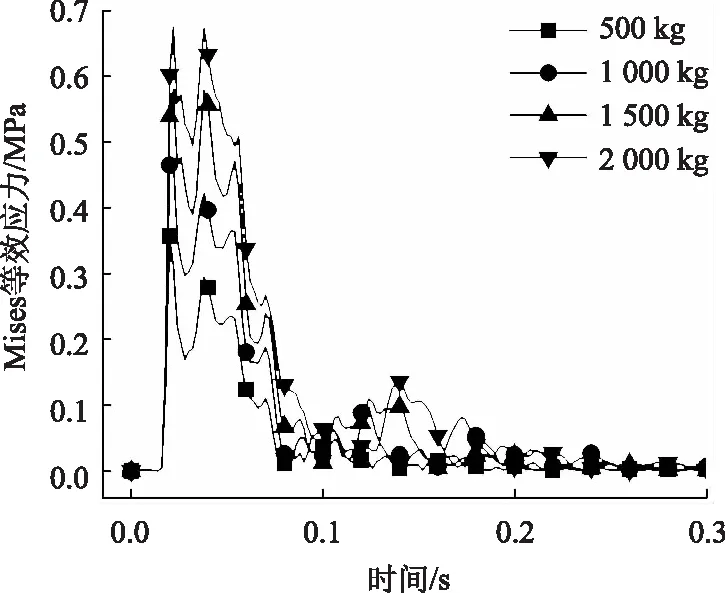
图8 Mises等效应力时程曲线

2.3 不同冲击角度

将冲击角度(角度默认为落石速度方向所在直线与缓冲层平面所夹的角)分别设置为：30°，45°，60°，75°，90°，其他参数见表2。

2.3.1 冲击力对比分析

不同冲击角度下法向冲击力时程曲线如图9(a)所示。时程曲线的变化趋势基本相同，法向冲击力随时间增长均为先急剧增大后逐渐减小，且呈现脉冲状变化。冲击角度从30°增加到90°时，法向冲击力从386.62 kN增加到803.60 kN；冲击持续时间由0.154 s减小至0.084 s。分析表明，法向冲击力与落石冲击角度呈正相关，冲击角度为90°时法向冲击力最大(即垂直冲击)；落石冲击持续时间与落石冲击角度呈负相关。

不同冲击角度下切向冲击力时程曲线如图9(b)所示。时程曲线的变化趋势基本相同，切向冲击力随时间增长均为先增大后逐渐减小，且呈现脉冲状变化。冲击角度从30°增加到90°时，切向最大冲击力先增大后减小，如图10所示。当冲击角度为45°时，切向最大冲击力达到最大，为206.29 kN；当冲击角度为90°时，切向冲击力为0。

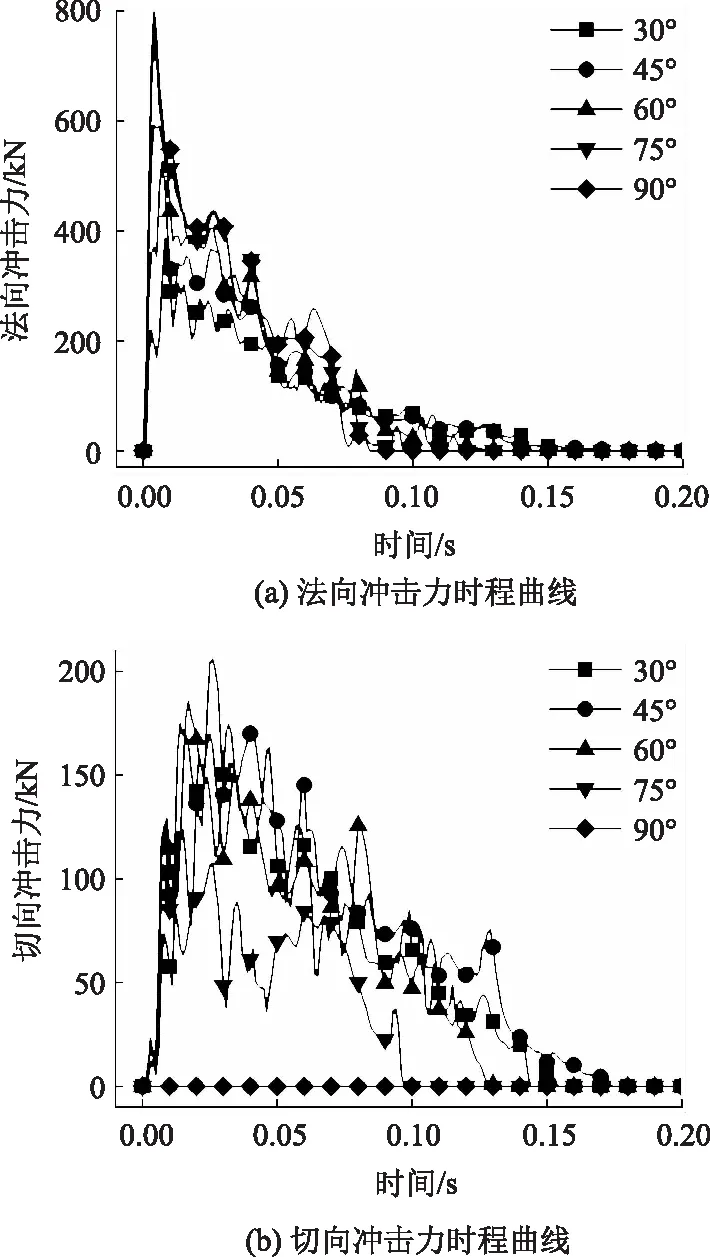
图9 冲击力时程曲线

图10 切向最大冲击力变化曲线

2.3.2 冲击变形对比分析

不同冲击角度下法向最大位移时程曲线如图11(a)所示。时程曲线形状基本相同，法向最大位移均是在极短时间内近似线性增长至某一最大值，随后产生一部分回弹进而达到稳定。冲击角度从30°增加到90°时，产生的法向最大位移从0.252 m增加到0.577 m。分析表明，法向最大位移与落石冲击角度呈正相关。

不同冲击角度下切向最大位移时程曲线如图11(b)所示。时程曲线的形状基本相同，切向最大位移均是在极短时间内近似线性增长至某一最大值，随后达到稳定。冲击角度从30°增加到90°时，产生的切向最大位移从0.699 m减小到0.219 m。分析表明，切向最大位移与落石冲击角度呈负相关。

图11 最大位移时程曲线

2.3.3 Mises等效应力对比分析

不同冲击角度下Mises等效应力时程曲线如图12所示。时程曲线的形状基本相同，Mises等效应力初始一段时间为0，之后随时间增长均为先急剧增大后减小至稳定，且呈现脉冲状变化。冲击角度从30°增加到90°时，最大Mises等效应力从0.229 MPa增加到0.539 MPa，均未达到混凝土抗拉强度1.1 MPa，拦石墙安全。分析表明，最大Mises等效应力与落石冲击角度呈正相关。

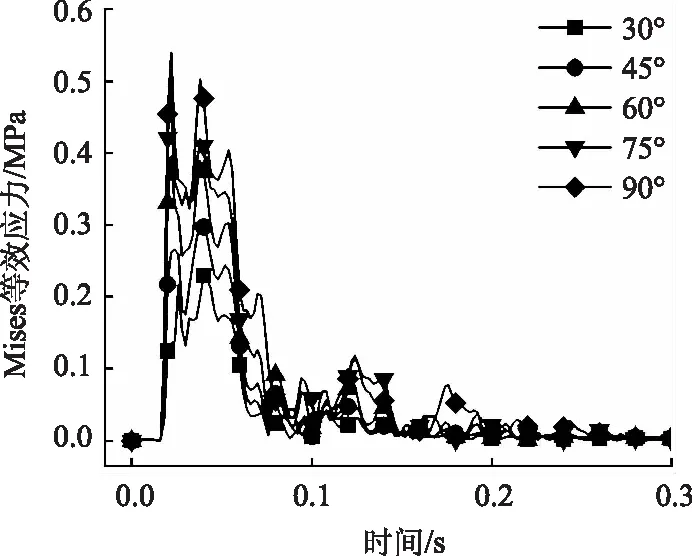
图12 Mises等效应力时程曲线

通常情况下，落石脱离母岩后，在重力作用下一般为竖直下落，因此要在条件允许的情况下适当增大缓冲层的坡度，可以有效减小落石冲击缓冲层的角度，降低对拦石墙的损伤。

2.4 不同落石形状

之前的讨论都是将落石假定为球体，而实际工程中的落石形状不一，大体可分为长方体和球体，需要对不同形状的情况加以分析。将落石体积固定为0.523 6 m3，此时球体半径为0.5 m, 长方体尺寸为：(1)0.806 m×0.806 m×0.806 m，接触面为0.806 m×0.806 m；(2)0.987 m×0.987 m×0.537 m，接触面为0.987 m×0.987 m；(3)1.140 m×1.140 m×0.403 m，接触面为1.140 m×1.140 m。其他参数见表2。

2.4.1 冲击力对比分析

不同落石形状下冲击力时程曲线如图13所示。冲击力随时间增长均为先急剧增大后迅速减小至稳定。当落石形状为球体时，最大冲击力仅为804 kN；而当落石形状为长方体时，最大冲击力急剧增大，尤其是接触面为1.140 m×1.140 m时，最大冲击力达到5 693.32 kN，为球体的7倍。分析表明，落石形状对冲击力的影响较大，长方体形状落石冲击产生的冲击力要远大于球体，且与缓冲层接触面积越大，冲击力越大。

图13 冲击力时程曲线

2.4.2 冲击变形对比分析

不同落石形状下最大位移时程曲线如图14所示。时程曲线的形状基本相同，最大位移均是在极短时间内近似线性增长至某一最大值，随后产生一部分回弹进而达到稳定状态。当落石形状为球体时，产生的最大位移达到了0.585 m；而当落石形状为长方体时，最大位移急剧减小，接触面为1.140 m×1.140 m时，最大位移为0.15 m，仅为球体的1/4。分析表明，落石形状对最大位移的影响较大，长方体形状落石冲击产生的最大位移要小于球体，且与缓冲层接触面积越大，最大位移越小。

图14 最大位移时程曲线

2.4.3 Mises等效应力对比分析

不同落石形状下Mises等效应力时程曲线如图15所示。时程曲线的形状基本相同，Mises等效应力初始一段时间为0，之后随时间增长均为先急剧增大后减小至稳定，且呈现脉冲状变化。当落石形状为球体时，最大Mises等效应力为0.539 MPa;而当落石形状为长方体时，最大Mises等效应力急剧增大，接触面为1.140 m×1.140 m时，最大Mises等效应力为3.166 MPa，是球体的6倍，超过混凝土抗拉强度1.1 MPa，需进行加固处理。分析表明，落石形状对Mises等效应力影响较大，长方体形状落石冲击产生的最大Mises等效应力大于球体，且与缓冲层接触面积越大，最大Mises等效应力越大。