考虑信息诱导的随机均衡交通流逐日演化模型

郑玉馨，胡志华

(1.上海海事大学 青岛研究院，山东 青岛 266034；2.上海海事大学 物流研究中心，上海 201306)

0 引言

随着信息技术和通信技术的迅速发展，城市智能交通系统(Intelligent Traffic System，ITS)的应用越来越广泛。作为ITS的重要组成部分，交通诱导系统(Traffic Guidance System，TGS)通过发布交通信息对出行者进行预期路径诱导，以缓解交通拥堵、提高通行效率[1]。为保证准确性，同时尽可能真实地反映路网状态，TGS需要对交通信息进行日复一日的反馈与修正。由于交通信息具有时变性，出行者可能动态地调整他们的出行路径，使得路段或路径流量在达到均衡态之前随着时间而演化。因此，考虑动态交通信息对出行决策的影响可以更加准确地描述出行者的行为规律和交通流的分布形态，具有较强的现实意义。

交通流平衡分配问题是交通网络研究的热点。目前，关于静态交通分配的研究集中于用户均衡(user equilibrium，UE)和随机用户均衡(stochastic user equilibrium，SUE)两个方面[2]。Wardrop等[3]提出的用户均衡原则是基于出行者完全理性的假设，出行者拥有完备的路网信息且始终选择出行阻抗最小的路径。但在现实情况中，出行者通常是有限理性的，由于无法掌握完整可靠的路网信息，出行者感知的路径阻抗与实际路径阻抗会存在一定的偏差。基于此，随机用户均衡模型为出行者的感知路径阻抗引入随机误差项，并通过离散选择理论描述出行者的路径选择行为。

以上关于静态交通分配的研究均认为在路网出行者数量固定的情况下，各路径流量可按相应的路径选择规则预先获知，即假设网络均衡态一定可以实现[4]。这类模型仅关注路网最终的平衡态，未考虑路网状态与出行者行为之间的相互影响，忽视了网络从非平衡态向平衡态演化的过程。已有研究指出，网络交通流演化是大量出行者在经验和信息的共同作用下进行复杂的非合作博弈的过程，出行者的路径选择行为受已知路况信息、个体理性程度和习惯偏好等多种因素的影响。根据出行者对交通信息的接受程度，度巍等[5]将出行者分为保守和乐观两种类型，通过仿真试验分析了路网中保守型出行者数量对交通流演化的影响，保守型出行者所占比例越大，均衡态下的路径阻抗越大，路径流量越小。

由于决策干扰因素的不确定性和时变性，学者们将有限理性[6]、前景理论[7]、后悔理论[8]应用到交通分配问题的建模与分析中，使研究背景更符合现实生活。为了更好地描述出行者在不确定环境中的决策行为，同时深刻理解网络交通流的演化规律以及路网均衡态的可达性，学者们在逐日动态模型(以天数为递归单位)的研究上做了大量的工作[9]。现有文献主要从两个途径来分析网络交通流逐日动态演化规律：(1)从个体角度出发，以出行者个体为单元，通过计算机仿真和行为试验等方式模拟网络交通流逐日演化过程；(2)从群体角度出发，以非线性动力学理论为基础，通过建立动态交通分配模型来研究出行者的逐日路径选择机理以及网络平衡态的存在性和稳定性，通常可根据出行时间变量的类型将动态交通分配模型分为连续型动态系统和离散型动态系统[10]。张波等[11]运用均衡和演化两种分析方法，研究了出行者路径选择行为与动态交通系统之间的相互作用规律，为用户均衡的实现过程提供合理的解释。Guo等[12]提出建立一个动力学系统模型，用路段流量变量模拟交通流的演变过程，该模型的不动点等价于用户均衡态。Bifulco等[13]考虑信息在交通网络中的作用，重点分析了交通信息影响下路网流量演化的收敛性和稳定性。综合考虑出行时间(价格)和路径通行能力(数量)对出行者路径选择行为的影响，黄中祥等[14]分别建立了价格调节、数量调节以及价格-数量共同调节3个交通流动态演化模型，通过分析得知3种演化模型对应了3种用户均衡模式，均可较好地描述网络交通流演化过程。在探究网络交通流逐日动态演化规律的同时，学者们还研究了使流量出现分岔或混沌的影响因素，并提出了有效的控制方法[10]。

现有文献大多从信息提供方的角度来分析交通信息对出行者路径选择行为的影响，着重于是否提供信息服务以及信息服务的优劣。郭仁拥等[15]模拟了路网流量的逐日演化和先进出行者信息系统市场占有率的逐年演化过程，重点分析了采用信息服务对出行者路径选择行为的影响。阎昊等[16]认为网络交通流演化的收敛性和稳定性与出行者对历史经验的依赖程度和交通信息系统的使用率有关。本研究在文献[15]的基础上，从信息接收方——出行者的角度入手，在信息一致的前提下，考虑出行者是否信任交通诱导信息对交通流演化的影响，将出行者对路径诱导信息的信任决策以及诱导信息作用下出行者的路径选择行为纳入交通流逐日演化模型，并对模型进行性质分析，最后结合算例详细分析了出行者的行为惯性、感知误差、决策误差以及信任行为模式对交通流演化收敛速度和最终平衡态的影响。

1 交通流逐日演化模型

本研究假设路网中出行者数量是固定的，所有出行者同质且同时出发。其中，出行者同质是指在整个演化进程中，所有出行者拥有相同的时间价值、偏好体系等属性，不包括出行者每日的路径选择行为和信息信任决策；同时出发是指所有出行者每日都同时出发。假设交通流逐日演化过程如图1所示，路网中各路径的实际出行阻抗由路径流量确定，实际出行阻抗为路径诱导信息提供依据，路径诱导信息通过改变出行者的感知出行阻抗来影响出行者的路径选择行为，继而影响出行者的平均出行收益和信息信任决策。但由于信息具有时变性和滞后性，不管信任与否，出行者通常不会完全服从接收到的信息，而是结合历史经验进行出行决策。

图1 交通流逐日演化过程

考虑出行者的信息信任决策不同，本研究将出行者分为两类：(1)信任路径诱导信息的出行者;(2)不信任路径诱导信息的出行者。信任路径诱导信息的出行者对诱导信息的信任度很高，他们虽然也具有历史出行经验，但更偏好根据每日提供的路径诱导信息来调整出行路径，因此，该类出行者对真实路径阻抗的感知误差较小，有更大的概率选择出行阻抗较小的路径。与信任诱导信息的出行者相比，不信任路径诱导信息的出行者对诱导信息的信任度较低，他们更倾向于根据自身的出行经验进行路径选择，因此，该类出行者对真实路径阻抗的感知误差较大，其出行行为具有一定的惯性。此外，出行者的信息信任决策是根据每日诱导信息为出行者带来的平均出行阻抗节省量发生动态变化的。若当日所有信任路径诱导信息出行者的平均出行阻抗高于所有不信任路径诱导信息出行者的平均出行阻抗，则翌日出行者对路径诱导信息的信任度会降低，部分出行者由信任诱导信息变为不信任诱导信息，所有出行者中信任诱导信息的出行者比例也随之下降，反之亦然。

1.1 交通流模型

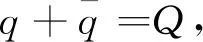
(1)

(2)

(3)

(4)

假设各路段的出行阻抗仅与路段流量有关，定义路段a∈A的实际出行阻抗为ua，采用经典的BPR(Bureau of Public Road)函数表示路段流量va与出行阻抗ua的关系。在式(5)BPR函数中，Ta为“自由流”时路段a的平均行驶时间，Ca为路段a的通行能力。

(5)

路径r∈Rw的实际出行阻抗ur是其所经过的所有路段的实际出行阻抗之和，如式(6)所示。

(6)

(7)

(8)

1.2 信任决策模型

对于路径诱导信息，出行者仅有信任和不信任两个选择，因此根据离散选择原理，使用二元Logit模型来描述出行者对诱导信息的信任决策。式(9)～(10)描述了出行者对诱导信息的信任决策与信息为其带来的出行收益(出行阻抗节省量)之间的关系。路网中两类出行者的平均出行阻抗差值越大，信任诱导信息出行者的信息收益越高，继而越来越多的出行者选择信任路径诱导信息。在下文中，所有出行者中信任路径诱导信息的出行者比例π，简称为信息信任比例，其定义如式(11)所示。

(9)

(10)

(11)

式(9)～(11)中μ为决策误差参数，较大的值意味着较小的决策误差。

1.3 感知阻抗更新模型

Gr=gr+εr,

(12)

(13)

gr[d+1]=ω·ur+(1-ω)·gr[d],

(14)

(15)

1.4 路径选择模型

(16)

(17)

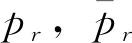
fr[d+1]=γ·q·pr+(1-γ)·fr[d],

(18)

(19)

1.5 交通流逐日动态演化模型

式(14)可以用更一般的形式表示[17]，即式(20)～(21)。

gr[t+Δt]=ω(Δt)·ur+[1-ω(Δt)]·gr[t],

(20)

gr[t+Δt]-gr[t]=ω(Δt)·(ur-gr[t])。

(21)

假设ω(Δt)是一个随Δt单调递增的函数，0≤ω(Δt)≤1，Δt为更新间隔的长度，Δt越大，出行者越少依赖过去的经验。当Δt=1时，式(20)等价于式(14)。当Δt→0，可以得到感知出行阻抗更新的1阶连续形式，即式(22)。

(22)

同理，离散动态系统(14)～(15), (18)～(19)可转换为连续动态系统(23)～(26)。

(23)

(24)

(25)

(26)

2 稳定性分析

定理1(Brouwer不动点定理) 若A⊂R且A为非空紧凸集，函数F:A→A是一个从A到A的连续函数，则该函数有一个不动点，即存在x∈A,x=F(x)。

推论1若路径阻抗函数连续可微且严格单调增加，则动态系统(18)～(19)存在一个不动点。

(27)

(28)

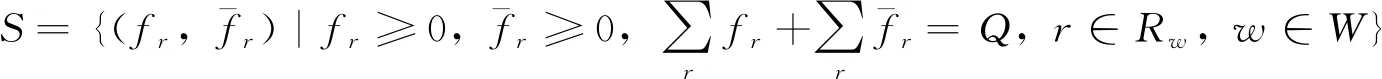
定理2若没有出行者能够通过单方面改变路径来降低自身的出行阻抗，则交通流达到随机用户均衡态[17-18]。

推论2若动态系统(14)～(15), (18)～(19)存在不动点，则该不动点的路径流量分布等价于交通流的随机用户均衡态。

(29)

(30)

(31)

(32)

定理3若动态系统在不动点处存在一个Lyapunov函数，则该不动点是稳定的[18]。

推论3假设连续可微函数

(33)

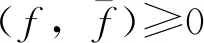
(34)

将动态系统式(25)～(26)代入式(34)得

(35)

综合推论1，推论2和推论3得出结论，若路径阻抗函数是连续可微的单增函数，且路径流量可行集为非空紧凸集，则动态系统(18)～(19)的不动点是稳定存在的，同时该不动点的路径流量分布等价于交通流的随机用户均衡态。

3 数值模拟算法

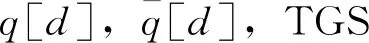
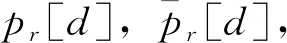
Step 4(终止条件) 若演化时间d已到达演化试验时间上限|D|，即d≥|D|，则终止计算，否则，转入Step 1。

4 数值试验

4.1 算例数据

建立一个由5条路段和4个节点构成的试验网络，如图2所示。OD对(1,4)之间有3条可行路径，路径1，2，3分别由路段1和4，路段2和5，路段1，3和5组成。

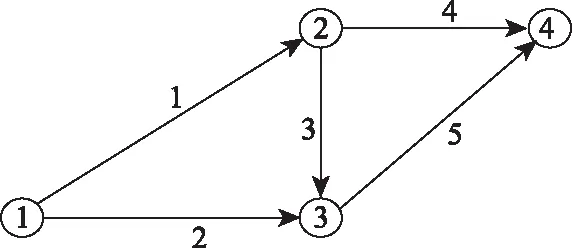
图2 试验网络

路网中出行者数量Q=1 000，BPR函数中的参数α=0.15，β=4，二元Logit模型中的决策误差参数μ=0.9。演化试验共持续100 d，各路段参数如表1所示，其他初始参数和初始路径流量如下：

表1 各路段参数

(f1[0],f2[0],f3[0])=(170,165,165),

4.2 算例分析

4.2.1 演化过程

使用4.1节算例数据进行计算，得到随机均衡交通流的逐日演化过程，如图3所示。

从图3可以看出，在交通流演化的开始阶段，路径流量是不稳定的，随着演化推进，路径流量的变化幅度越来越小，在第40 d前后收敛到不动点，即实现了路网交通流的平衡态。图3(d)中信任路径诱导信息的出行者比例并没有随演化推进一直增大，而是在一段时间的波动后到达稳定值，这是因为较高的信息信任比例会造成交通“移堵”现象，而波动幅度逐渐减小则说明诱导信息在交通流演化过程中发挥了积极作用。

图3 随机均衡交通流逐日演化过程

4.2.2 灵敏度分析

图4 路径重选率对随机均衡交通流演化的影响

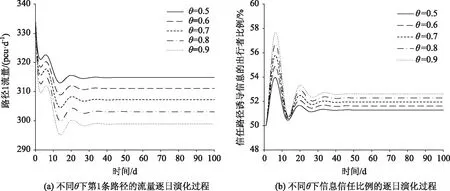
图5 感知误差参数对随机均衡交通流演化的影响

与感知误差参数θ同理，参数μ越大，决策误差越小。从图6中可以看出，当μ≤0.5时，路径1流量和信息信任比例的演化均无明显波动并且很快到达平衡态，这说明当μ∈[0.3,0.5]时，出行者是否信任诱导信息的决策更趋向于随机选择。当μ>0.5时，路径1流量和信息信任比例的演化收敛速度随着μ的增加而减慢，且变化幅度较大。决策误差的减小使出行者的行为决策更符合实际情况，出行者的信息信任比例也逐渐提升。

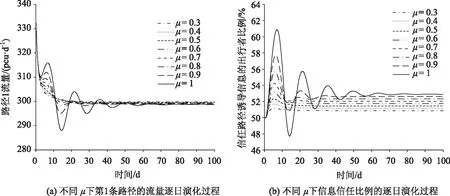
图6 决策误差参数对随机均衡交通流演化的影响

4.2.3 静态信息信任比例和动态信息信任比例下的路径流量逐日演化

图7对比了静态信息信任比例和动态信息信任比例下路径流量的逐日演化过程，其中，图7(a)～图7(c)分别描述了π为固定值0.25和固定值0.5以及π动态变化时3条路径各自流量的逐日演化过程。如图7(a)和图7(b)所示，3条路径各自的流量均在短时间内到达稳定状态，并且，π值越大，不同路径的流量差异越明显。图7(c)中3条路径各自的流量在演化初期都出现了较明显的波动情况，最终均在演化进行到第40 d左右时收敛到稳定值，并且路径2的流量波动幅度大于路径1和路径3的流量波动幅度。图7(d)以路径1为例，对比了不同π下路径流量的逐日演化过程，从该图中可以看出，当π取固定值时，路径流量大小与π值的大小成反比例关系，π动态变化时路径流量的稳定值小于π取固定值时该路径流量的稳定值。综合上述分析可知，当π随演化进程发生动态变化时，路径流量演化更容易受到诱导信息的影响，并且稳定状态下的交通流分布更符合路网的通行能力。因此，动态的信息信任比例对路径流量演化具有正向作用。

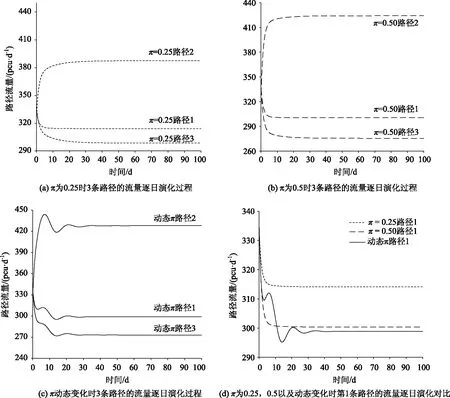
图7 静态信息信任比例和动态信息信任比例下的路径流量逐日演化对比

5 结论

研究结果表明，在一致性交通信息的指导下，选择信任路径诱导信息的出行者对出行阻抗的认知更为准确，更容易选择交通状况良好的路径，而不信任路径诱导信息的出行者对出行阻抗的感知比较局限，受行为惯性的影响较大，通常会受到更大的出行阻抗。对信任路径诱导信息出行者比例的相关演化过程进行对比分析可知，由于交通信息具有时变性和滞后性，当越来越多出行者选择信任路径诱导信息时，诱导信息对交通流的调控能力会被削弱，甚至出现负面的交通流聚集反应，导致交通“移堵”现象的产生，因此，交通流随机用户均衡态下信任和不信任路径诱导信息的出行者比率通常保持在一个稳定值。上述试验与分析是在出行者信息信任决策动态变化的前提下进行的，为了确保本研究的假设符合出行者的行为模式，对静态信息信任比例和动态信息信任比例下的交通流逐日演化进行了对比分析，验证了研究结果的合理性和准确性。

本研究结果将帮助决策者加深对城市路网交通流动态演化规律的理解，为交通网络规划、交通信息服务的评价以及交通诱导系统的优化提供理论支持，促进智能交通系统的不断完善和发展，提高路径诱导信息的合理性和有效性。目前，对信息诱导下交通流逐日演化模型的研究仅考虑了单一用户类别，未来可根据出行者的异质性，将时间价值、出行可靠性、决策偏好等纳入考虑范围，进一步研究多用户类的城市路网交通流动态演化规律。